FAST反射面形状调节策略研究
2021-02-28牟淼孔娅妮郭磊
牟淼 孔娅妮 郭磊





摘 要:文章综合考虑FAST上各个主索节点在经度方向、纬度方向上的位移变化和边缘光滑度等因素,研究了反射面的变形策略,借助粒子群算法,建立了较为符合实际的理想抛物面模型;然后利用欧拉旋转定理建立旋转模型,得到旋转后的理想抛物面模型,再通过旋转基准球面固定照明区域的方法,求得工作抛物面上照明区域内692个主索节点编号,伸缩量以及位置坐标;最后利用降维的技巧,求出基准球面和工作抛物面上的反射信号接收比。
关键词:变形策略;理想抛物面;旋转模型;接收比;粒子群算法;降维
中图分类号:TP181;P111.44 文献标识码:A文章编号:2096-4706(2021)16-0086-07
Research on Shape Adjustment Strategy of FAST Reflector
MOU Miao1, KONG Yani2, GUO Lei3
(1.School of Mechanical Engineering, Yangtze University, Jingzhou 434023, China; 2.School of Information and Mathematics, Yangtze University, Jingzhou 434023, China; 3.School of Physics and Optoelectronic Engineering, Yangtze University, Jingzhou 434023, China)
Abstract: In this paper, considering the displacement changes and edge smoothness of each main cable node in longitude and latitude direction on FAST, the deformation strategy of reflector is studied, and an more realistic ideal paraboloid model is established with the help of particle swarm optimization algorithm; then, the rotation model is established by using Euler rotation theorem, and the ideal paraboloid model after rotation is obtained. Then, by rotating the reference sphere to fix the lighting area, the number, expansion and position coordinates of 692 main cable nodes in the lighting area on the working paraboloid are obtained; finally, using the technique of dimension reduction, the reflection signal reception ratio on the reference sphere and the working paraboloid is obtained.
Keywords: deformation strategy; ideal paraboloid; rotation model; receiving ratio; particle swarm optimization; dimension reduction
0 引 言
中國天眼FAST是迄今为止世界上最先进的空间探测设备,可以接收到宇137亿光年外的电磁信号,由馈源支撑塔、主动反射面和馈源仓组成。本文将对2021年全国大学生数学建模竞赛题进一步研究,建立了合理的评估指标,利用“粒子群”搜索算法,寻找最为符合实际的理想抛物面模型,然后利用欧拉旋转定理旋转抛物面方程得到第一种旋转模型,旋转后的理想抛物面方程;再通过旋转基准球面得到第二种旋转模型,固定照明区域,逆向旋转基准球面,得到工作抛物面上照明区域内692个主索点编号,然后通过计算得到伸缩量以及位置坐标,最终利用“降维”的技巧,求得基准球面和工作抛物面上的反射信号比。
1 天眼FAST基本介绍
1.1 FAST的组成
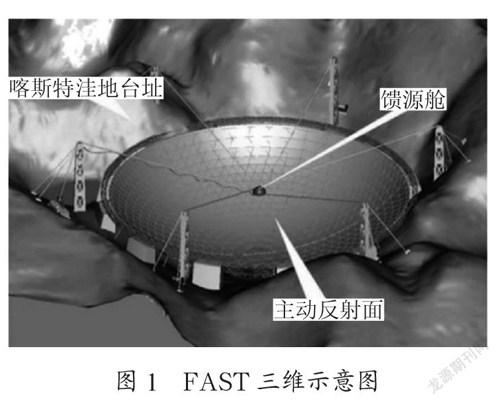
FAST主要由主动反射面,信号接收系统以及相关的控制、测量和支承系统组成,如图1所示。其中主动反射面是由主索网、反射面板、下拉索、促动器及支承结构等主要部件构成的一个可调节球面。主索面上每一个主索点处下端都通过下拉索与促动器连接,通过调节各个主索点对应的促动器的伸缩量进而实现反射面形状的调节。
1.2 主动反射面的基准态和工作态
主动反射面可以分为基准态和工作态两种状态,其中基准态时反射面可以看作是半径为300 m,口径为500 m的球面,而当主动反射面处于工作态时,反射面调节成口径为300 m的反射抛物面,图2是FAST处于工作态时剖面示意图,两个同心球面的半径差为F=0.466R,其中C点为基准球面球心,馈源舱接受平面的中心只能位于与基准球面同心的球面上,只有当反射信号经过以馈源舱中心为圆心,直径为1 m的圆盘时,才算接收到信号。
2 构建模型思路
本文的最终目的是求解基准球面和工作抛物面反射出信号的有效接收比,而为了求解工作抛物面的接收比,首先应求解工作抛物面上照明区域各个主索点对应促动器的伸缩量,又因为最优工作抛物面是在约束条件的情况下最接近理想抛物面的抛物面,所以要优先计算理想抛物面方程,具体思维结构如图3所示。为了得到比较符合实际的理想抛物面方程,本文从径向,纬向的位移变化和边缘光滑度等因素出发,建立符合实际的评价准则,利用“粒子群”优化算法拟合最优参数,最终求得结果。
3 确定理想抛物面方程
3.1 综合评价准则的确定
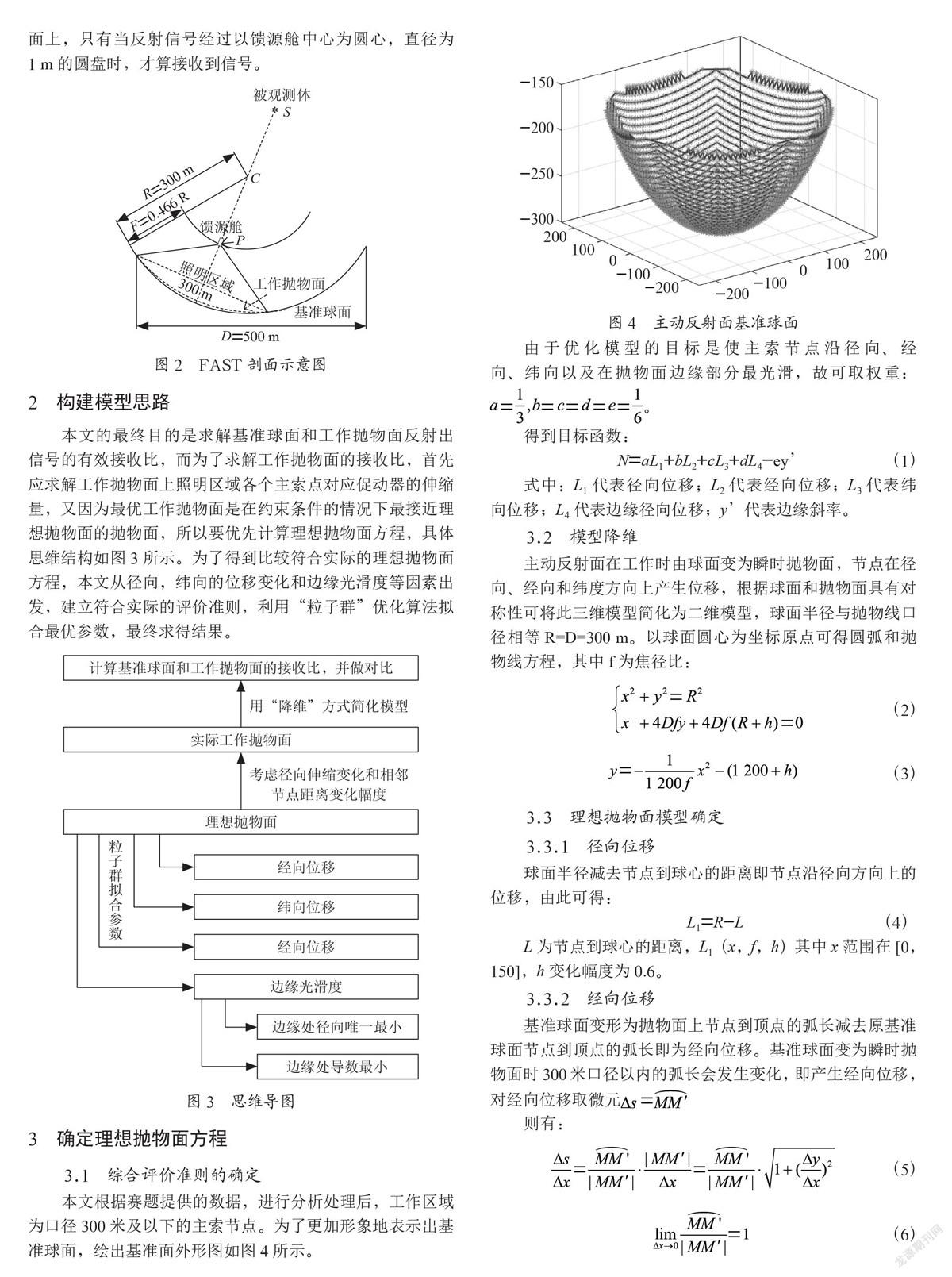
本文根据赛题提供的数据,进行分析处理后,工作区域为口径300米及以下的主索节点。为了更加形象地表示出基准球面,绘出基准面外形图如图4所示。
由于优化模型的目标是使主索节点沿径向、经向、纬向以及在抛物面边缘部分最光滑,故可取权重:。
得到目标函数:
N=aL1+bL2+cL3+dL4-ey’ (1)
式中:L1代表径向位移;L2代表经向位移;L3代表纬向位移;L4代表边缘径向位移;y’代表边缘斜率。
3.2 模型降维
主动反射面在工作时由球面变为瞬时抛物面,节点在径向、经向和纬度方向上产生位移,根据球面和抛物面具有对称性可将此三维模型简化为二维模型,球面半径与抛物线口径相等R=D=300 m。以球面圆心为坐标原点可得圆弧和抛物线方程,其中f为焦径比:
(2)
(3)
3.3 理想抛物面模型确定
3.3.1 径向位移
球面半径减去节点到球心的距离即节点沿径向方向上的位移,由此可得:
L1=R-L (4)
L为节点到球心的距离,L1(x,f,h)其中x范围在[0,150],h变化幅度为0.6。
3.3.2 经向位移
基准球面变形为抛物面上节点到顶点的弧长减去原基准球面节点到顶点的弧长即为经向位移。基准球面变为瞬时抛物面时300米口径以内的弧长会发生变化,即产生经向位移,对经向位移取微元
则有:
(5)
(6)
(7)
基准球面变形为抛物面后抛物线上主索节点M到顶点弧长为:
(8)
基准球面的主索节点M’到球面顶点弧长为:
经向位移:
L2=sM-sM’ (9)
3.3.3 径向位移
假定主索节点N在圆弧上的横坐标为x0,在抛物线上的横坐标x’,纬度环环长变化量为l,相对基准球面纬度环环长变化量为:
(10)
3.3.4 径向位移
抛物面变形边缘应尽量光滑,抛物线边缘处斜率与圆弧斜率应尽量接近,抛物线边缘径向移动位移与圆弧径向移动位移之差尽量小。
基准球面与抛物面连接处x0=150,y’0=0.577 4,抛物面的导数:
(11)
边缘径向位移:L4=L1(149.146 2,f,h)
故该题建立的“理想曲面优化模型”具体为:
目标函数:MinN=aL1+bL2+cL3+dL4-ey’
3.4 理想抛物面模型求解
3.4.1 搜索算法的构建
该问题本质上是多目标优化模型,通过“粒子群”智能优化算法(图5)的过程如下:
(1)确定各个参数的搜索区间[v1,v2];
(2)赋给每个指标一定的权重,确定综合评价标准为目标函数;
(3)初始化粒子位置,并计算此时综合评价指标;
(4)重复步骤(3),直至目标函数值逐步收敛于最优目标函数值;
(5)输出最优目标函数对应的各个最优参数。
3.4.2 理想抛物面模型的求解结果
将上述粒子群算法过程通过matlab迭代求解得出结果如图6所示,两个参数如下:
f=0.467 7,h=0.412 2 (12)
式中:f为焦径比;h为顶点移动距离。
故理想抛物面方程为:
理想抛物面与基准球面的拟合曲线如图7和图8所示。
4 确定工作抛物面方程和主索点的伸缩量
4.1 旋转后工作抛物面模型建立
首先选取在α=0°,β=90°时确定出的理想抛物面:
(13)
将抛物面进行绕坐标轴旋转即在三维空间下曲面绕x轴旋转一定角度,再绕y轴旋转至对称轴在α=36.795°,β=78.169°方向上,需要计算出绕轴旋转的角度。以基准球面球心为坐标原点理想抛物面对称轴为z轴建立直角坐标系,将天体看作一点投射至坐标面上連结各点,由此便得到了第一种旋转方法,如图9所示。
其中α为方位角,β为仰角,绕x轴旋转的角度为∠mcp,绕y轴旋转的角度为∠mcs。假设sc=a,则:
(14)
(15)
(16)
令,α和β已知,即确定了沿x轴,y轴的旋转角度,则可利用旋转矩阵对问题一中确定的理想抛物面进行旋转:
假设原抛物面上一点(x,y,z),首先对x轴进行旋转得到旋转后坐标(x1,y1,z1):
(17)
然后绕y轴进行旋转得到旋转后坐标(x2,y2,z2):
(18)
(19)
记:
故可以得到旋转后的理想抛物面,即在α=36.795°,β=78.169°时的理想抛物面方程:
(20)
4.2 工作抛物面上主索点伸缩量模型建立
对基准球面上所有的主索节点进行旋转,第一次旋转绕z轴旋转α角度,第二次旋转绕y轴旋转角度,即可完成旋转,第二种旋转模型如图10所示。
图10 第二种旋转模型
绕z轴旋转矩阵为:
(21)
绕y轴旋转矩阵为:
(22)
其中:α=36.795°,β=78.169°
选取其中在工作面范围(照明区域)内的主索节点,即x2+y2≤1 502。
根据这些点确定其位置坐标,计算各个主索节点与球心连线之间的直线方程,求出直线与理想抛物线的交点,即理想主索的位置坐标:
(23)
解出理想抛物面上主索节点的位置坐标,且已确定基准球面旋转后的主索节点,即可利用两点间的距离公式计算理想化的伸缩量如图11所示。
(24)
其中Ll为主索节点理想的伸缩量,即不受任何约束情况下的伸缩量。
接下来考虑约束条件,主要为:
(25)
其中Ls为实际的伸缩量,xi为第i个主索节点的原长度
根据以上约束条件,即可计算出每一个在工作区域内的主索节点的伸缩量以及相应的位置坐标:
4.3 工作抛物面模型的求解
利用第一种旋转方式旋转所得理想抛物面如图12所示,其求解理想抛物面:
α=36.795°,β=78.169°
定义随机变量x,y,z
N=-arctan(cos(α)cos(β))
a=zeros(3);b=zeros(3)
带入原理想方程可得旋转后的理想方程:
b(3)=1/561.24×(b(1)2+b(2)2)-300.212 2
根据以上步骤,即可得出处在α=36.795°,β=78.169°时的理想抛物线方程:
4.4 工作抛物面上主索点伸缩量模型求解
4.4.1 利用第二种旋转方式求解顶点坐标
将基准面的顶点A0(0,0,-300.212 2)进行旋转,令:
即得顶点坐标G(-49.289,-38.866,-293.835)
4.4.2 求解各工作区域主索节点的编号及对应的位置坐标和伸缩量
求解旋转后主索节点的编号,可将整个基准球面旋转α=36.795°,β=78.169°,将工作区域移到球心的正下方,旋转后所有主索节点的位置坐标满足:x2+y2≤1502,将满足该条件的主索节点与球心相连,与第一问中理想抛物面的交点即为理想位置坐标。相邻节点距离变化幅度需要不超过0.07%,节点径向移动距离要在0.06以内,故计算基准球面上相应主索节点坐标和理想位置坐标的距离,根据约束条件进行约束,可导出相应伸缩量如表1所示。
5 确定基准球面和工作面的反射信号接收比
馈源仓是一个面积为0.785平方米的圆盘,需要计算出调节后馈源仓的接收比和基准反射球面的接收比,并将二者进行比较。本文先将基准反射球面进行旋转,让工作区域恰好与竖直照明区域一致,基准球面第一次旋转绕z轴旋转α角度,第二次旋转绕y轴旋转角度。
5.1 建立基准反射球面的反射信号接收比模型
由于基准反射球面具有各向同性,故可将基准反射球面简化为二维曲线。又因为圆弧关于z轴对阵,故只需考虑x∈(0,150),如图13所示。
在照明区域圆弧上,从0°至150°,取x步长为0.1的1 500个点,然后根据圆弧的方程曲线:
x2+y2=3002 (26)
算出对应点的y值,即可得到每个点的坐标。图13中
馈源仓距离球心(1-0.466)R,故:
L=[y-(1-0.466)R]·tan(2θ) (27)
若|L|≥0.5则不能有效接收,反之则能有效接收。
计算1 500个点中,能被接收到的点有多少个,即可计算出接收率。
5.2 建立工作抛物面上反射信号接收比模型
根据第二问求出的顶点坐标,计算出对称轴的直线方程。
天体发出的电磁波视為直线传播,平行对称轴射入,设入射电磁波方程为:
ax+by+cz+di=0 (28)
式中:a,b,c均已知,与对称轴方程的系数相同。
根据每个主索节点的坐标,即可计算出每个主索节点对应的di。
主索节点与球心的连线方程为:
(29)
式中:xi,yi,zi为各个主索节点的坐标。
将(28)绕(29)旋转180度即可得到新的直线方程:
Ax+By+Cz+D=0 (30)
又因为馈源舱的有效接收区域容易取得,即为满足如下条件:
(31)
本文即可认为此主索节点上的信号可以有效接收到。
记共有n个主索节点在工作区域,有m个主索节点可以被有效接收到,所以可得接受率为:
(32)
式中:ξ为有效接收率。
5.3 求解基准球面和工作抛物面上反射信号接收比模型
根据物理模型球面反射,由于天体与地球的距离足够可以将天体发出的电磁波看作平行波直线射入,需要得到最优的信号之比。馈源仓可视为一个小圆盘,接收反射的电磁波,由于实际情况下会有部分射入部分落在了范围之外,射在曲面上的坐标与反射到达焦面的坐标是非线性关系,故本文可对其进行机器学习的数据处理,使其在更高维度呈线性关系。
本文采用多项式核函数:
K(x,xi)=[p(xt·x)+s]q (33)
将输入集射入电磁波与曲面的交点坐标F(f1,f2,f3…fm)通过选取的多项式核函数映射到高维空间得到X(x1,x2,x3…xn),本文将输出的表达式表示为:
(34)
其中θ为本文要求的参数权值,根据损失函数计算公式:
(35)
结合选取的多项式核函数可以得到两种损失函数:cost0,cost1,如图14和图15所示。
对于基准球面接收比的求解为:8.51%;对于调整后抛物面接收比的求解为:83.20%。
6 结 论
本文针对FAST反射面形状调节进行了研究,首先通过机理建模的方式,从径向,纬向,经向方向上位移的变化以及边缘光滑度等因素出发,建立了综合评价准则,利用“粒子群”智能算法,搜索出符合各個因素的最优参数,从而得到符合实际的理想抛物面方程。在理想抛物面确定的情况下,利用两种旋转方式分别求出旋转后理想抛物面方程以及旋转后照明区域内主索点的伸缩变化量和理想抛物面顶点坐标,从而得到在符合约束条件的工作抛物面模型,最后再分别计算工作抛物面模型和基准球面模型的反射信号接收比。
在实际中,本文建出抛物面最佳变形策略模型,对于家用电视天线的形状设计,声、波接收面的优化等具有较强的指导意义。同时给FAST天眼提供了较好的变形策略,有利于更好的接收信号。
参考文献:
[1] 李明辉,朱丽春.FAST瞬时抛物面变形策略优化分析 [J].贵州大学学报(自然科学版),2012,29(6):24-28+43.
[2]朱丽春.500米口径球面射电望远镜(FAST)主动反射面整网变形控制 [J].科研信息化技术与应用,2012,3(4):67-75.
[3] 王璐.大型阵面位姿调整系统的布局优化和协调控制研究 [D].哈尔滨:哈尔滨工程大学,2019.
[4] 卓金武,李必文,魏永生,等.MATLAB在数学建模中的应用:第2版 [M].北京:北京航空航天大学出版社,2013.
[5] 天工在线.MATLAB从入门到精通 [M].北京:中国水利水电出版社,2018.
作者简介:牟淼(2000.09—),男,汉族,山东济南人,本科在读,研究方向:机械工程;孔娅妮(2001.11—),女,汉族,湖北咸宁人,本科在读,研究方向:数学与应用数学;郭磊(2000.08—),男,汉族,山东济南人,本科在读,研究方向:应用物理。
