基于改进K-Means聚类算法的移动5G手机用户分类研究

◆毛建军

基于改进K-Means聚类算法的移动5G手机用户分类研究

◆毛建军

（云想科技有限公司 江苏 210000）

；随着5G时代的来临，为了对5G手机用户提供更具有针对性的个性化服务，本文对当前移动5G手机用户的消费使用情况进行了分析，数据经过清洗处理后，运用K-Means算法对移动5G手机用户消费情况进行了分类，在科学分类的指导下，为营销部门开展针对性地营销提供了理论支持，为客户提供更全面的服务，节省了服务成本，提升企业竞争力。

K-Means算法；聚类分析；移动5G

1 背景

当前，国内5G通信行业以移动、联通、电信以及广电为主要通信经营服务商。在剧烈的竞争现状的背景下，对移动的服务水平、营销专业度、服务内容、服务质量等方面提出了更高层次的标准。同时，客户对通信服务的个性化要求越来越高，用户的使用场景、通话使用时长，流量用量等多方面都有着较大地差异。本文通过改进K-Means聚类算法分析移动5G手机用户消费情况从中发现不同用户之间存在的消费共有特征，然后对同一消费情况特征类别下的5G手机用户提供定制化服务，满足用户需求，降低企业的管理费用，提高企业核心竞争力。

2 数据展示

本文研究数据来自移动公司客户经营管理数据库，共提取5000条数据进行分析，通过分析结果指导经营活动评估实际的分类效果，从而应用到日常的数据分析工作中，原始数据的内容如下表1所示：

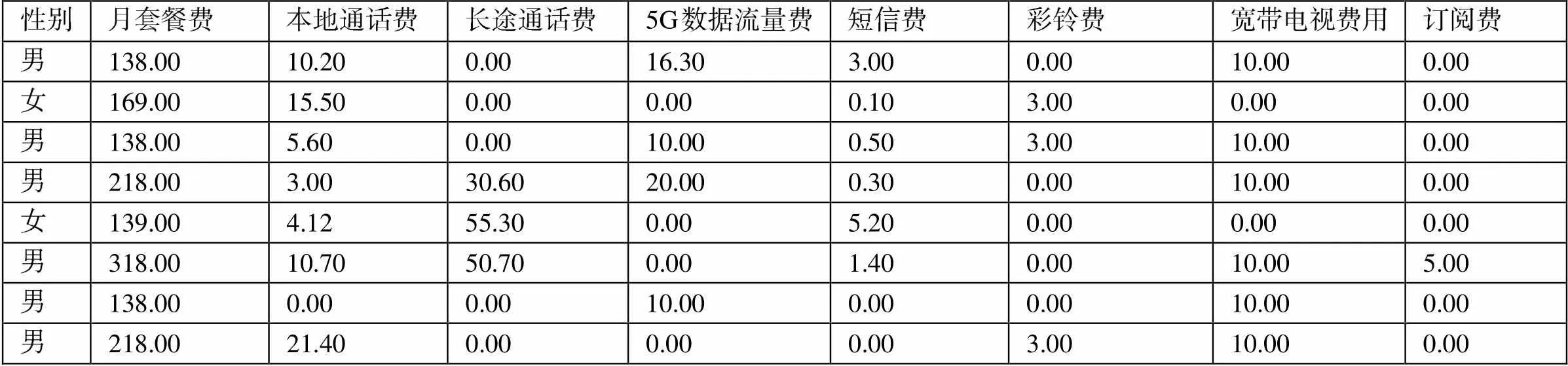
表1 5G手机用户消费数据表

由表1可知，原始数据表中共有数据项8个，分别是月套餐费、本地通话费、长途通话费、5G数据流量费、短信费、彩铃费、宽带电视费以及订阅费构成，原始数据中存在一定的不完整、信息缺失的个体样本，需要对数据进行检查。同时，在进行聚类分析之前需要数据的预处理。

3 数据处理

通过人工方式进行数据清洗、数据选择等操作将信息异常的数据进行清除，以免对聚类分析造成分类影响。在对总数5000条样本的检查过程中，发现120条数据不符合分类要求，最后进行分析的样本空间为4880条有效数据。在进行K-Means聚类分析之前，需要对样本空间的每条数据的特征项做预处理，将无关特征项的影响降到最低。

3.1 数据标准化

通过z-score方法处理后的数据处在同一数量级且没有单位的数值，此时的数据就可以进行K-means聚类分析。经过标准化处理后的属性的数据处于同一量级，数据之间具有可比性，标准化处理的数据结果如下表2所示：

表2 标准化后的特征数据

由表2可知，经过标准化处理后的特征项的值，无法直观的判断分类情况，此时需要K-Means算法进行下一步的聚类的分析。

4 K-Means算法及分析过程

1967年，James MacQueen 在《Some methods for classification and analysis of multivariate observations》中提出“K-Means”。当前K-Means聚类算法主要应用有：文档分类器、客户分类、配合遗传算法和无人机解决商旅车行车路线问题，乘车数据分析等。

4.1 K-means算法

传统的K-Means聚类算法流程如下：首先，设置进行聚类的分类个数K，进行数据的初始化，随机从样本空间中的所有样本中选择K样本作为聚类的中心；然后分别得到样本空间中每个样本到所有聚类中心的距离，将与每个中心最近的样本归为该中心的同类中；再次，将同聚类中的所有样本数据的特征取平均值，将平均后得到的点作为新的聚类中心；最后，重复第上述步骤直到聚类中心不再改变即可。最后得到的分类结果就是最优的。在实际的计算代码中，K-Means算法的计算样本与分类中心的距离所使用的方法是欧几里得距离，如下公式1所示：

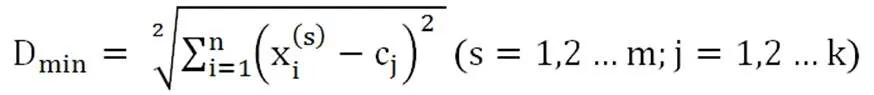
其中x1，x2，…，xn是样本x的n维特征项，c1，c2，…，ck是初始化的K个聚类中心，s1，s2，…，sm是样本空间中的m个体样本总数，计算样本x到所有k个聚类中心的距离然后选取距离最小的中心，将该样本x归类为此聚类中心的同类中。但是这种距离计算方式并没有考虑到样本的特征维度的权重性，而是将个体样本中的所有特征都对分类结果有同样的权重效果，这样的结果会导致分类结果的不准确性增大，即有的维度对分类结果影响大，有的维度对分类结果影响较小或几乎没有影响，对原有算法进行改进就十分有必要，改进的公式2如下所示：

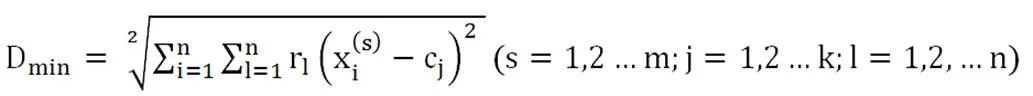
其中rl是特征x的n维的权重向量，取值范围在0-1之间，权重总和为1。通过对原有的算法的改进，使得原有的算法不支持多维权重的距离公式现在可以支持不同特征项的不同权重的距离公式，增加了算法的实用性和操作性，在面对实际问题时，能够突出某些样本中重要特征项的权重，减少弱相关特征项的干扰，保证了K-Means算法聚类分类的准确性。

4.2 K-Means聚类分析过程

原始数据表中共有数据项8个，分别是月套餐费、本地通话费、长途通话费、5G数据流量费、短信费、彩铃费、宽带电视费以及订阅费构成，通过对比数据可知彩铃费、宽带电视费以及订阅费对分类几乎没有区分度，设定的权重最小，而5G数据流量、短信费区分度较小，权重设定就大一些，月套餐费、本地通话费、长途通话费是消费主特征，所以权重设置最大，通过对不同的特征项设定不同的特征权重来确保分类的准确度，同时聚类个数K的选择对聚类的结果有着重要的影响，所以数据的聚类一次无法完成训练结果，需要根据不同的权重和不同的聚类个数训练结果进行不断的调整。本文通过调整权重参数和改变聚类的个数，分别进行了多次K-Means聚类训练了2-9个聚类情况下，得到的不同的分类结果，利用肘部法则选择最佳的聚类分类中心个数，如图1所示：

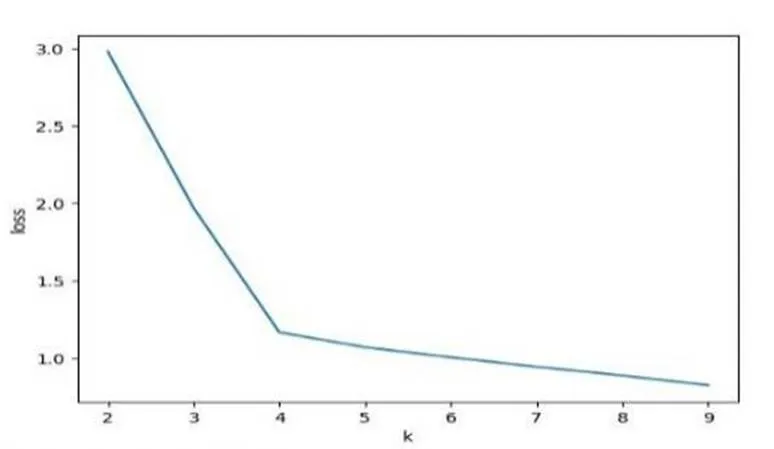
图1 K-Means不同聚类个数的情况

由图1可知，通过对数据进行2-9个聚类的分析得到的肘部法则图，只有在第4类的差异时较小，所有最佳分类聚类个数为4，同时确定最后的权重系数r=（0.2，0.2，0.2，0.15，0.1，0.05，0.05，0.05）。

4.3 聚类分析结果

选择聚类个数为4个分类后，得到结果如下表3所示：

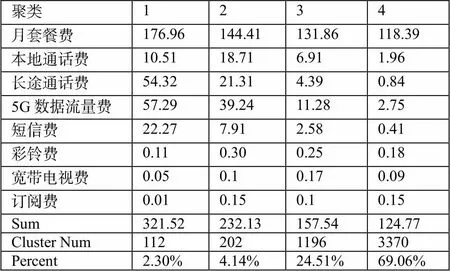
表3 K-Means分类结果

由表3可知，用户总共被分为4类，其中第一类用户的总数为112，占总样本空间的2.30%；第二类用户的总数为202，占总样本空间的4.14%；第三类用户的总数为1196，占总样本空间的24.51%；第四类用户总数为3370，占总样本空间的69.06%。第一类用户占比最少，月消费额最高，而且其月租费、长途通话费在占比中都是最高的，由此判断该类用户属于商务人士且经常出差，是联通手机用户中的最优质客户资源，是营销人员重点服务对象。第二类用户占比较一类用户多，其月消费水平也处于第二位，其5G数据流量费用支出较高，由此推测该类用户属于高流量用户，月流量消费很高，可对其提供偏向流量的套餐服务。

5 总结

本文利用改进的K-Means算法，通过改变算法中计算欧几里得距离增加维度权重的方法，提升了算法的针对性和适用性，并应用在对移动5G手机用户消费情况进行了聚类分析，比较不同聚类数量分类情况下的分类效果，成功实现了对当前移动5G手机用户的分类，为营销部门开展个性化营销活动提供了理论支持，在科学分类的有效指导下，可以提高服务的准确度，为客户提供更全面的服务。

[1]李敏. K-means算法的改进及其在文本聚类中的应用研究[D].江南大学，2018.

[2]李游. 基于校园网的用户行为分析研究[D].云南大学，2013.

[3]吴斌. 基于数据挖掘技术的学生成绩分析评价与研究[D].南昌大学，2009.

[4]Guo Xiaojie，Chen Liang，Zhou Hang，Huang Jun. An Improved K-means Algorithm and Its Application in the Evaluation of Air Quality Levels[A]. 东北大学、IEEE新加坡工业电子分会.第27届中国控制与决策会议论文集（下册）[C].东北大学、IEEE新加坡工业电子分会：《控制与决策》编辑部，2015：6.

[5]Youguo Li，Haiyan Wu. A Clustering Method Based on K-Means Algorithm[A]. Information Engineering Research Institute， USA.Proceedings of 2012 International Conference on Solid State Devices and Materials Science（SSDMS 2012 V25）[C].Information Engineering Research Institute， USA：智能信息技术应用学会，2012：6.

[6]史秀岭. K-means聚类优化算法的研究[D].长沙理工大学，2011.

[7]冯超. K-means聚类算法的研究[D].大连理工大学，2007.

[8]陈敏，李雪峰. 一种选择了初始聚类中心的改进K-means算法[A]. International Communication Sciences Association， Hong Kong.Proceedings of 2010 International Conference on Broadcast Technology and Multimedia Communication（Volume 2）[C].International Communication Sciences Association， Hong Kong：智能信息技术应用学会，2010：4.

[9]刘玥. 基于改进的K-means算法的银行客户聚类研究[D].吉林大学，2016.

[10]黄继超. k-means算法若干改进和应用[D].中南大学，2013.

[11]Xian Liang，Fuheng Qu，Yong Yang，Hua Cai. A Highly Efficient Fast Global K-Means Clustering Algorithm[A].Information Engineering Research Institute， USA.Proceedings of 2015 2nd International Conference on Civil，Materials and Environmental Sciences（CMES 2015）[C].Information Engineering Research Institute，USA：智能信息技术应用学会，2015：4.