基于余切相似度和BP神经网络的相似度快速计算

乔 非，关柳恩，王巧玲

（同济大学电子与信息工程学院，上海201804）

随着云计算等信息技术的发展，大数据日益渗透于金融、医疗、工业等各个行业领域之中，成为重要的生产因素。因此，对海量数据的挖掘和应用具有十分重要的现实意义，然而在实际生产过程中，大数据往往伴随着数据质量问题。相似度度量作为数据质量评估的重要方面，能够挖掘数据集中各数据间的相似程度，为数据分析提供准确和有效的依据。传统相似性度量方法分为基于距离度量方法和基于相似系数度量方法，基于距离度量方法主要有欧氏距离、曼哈顿距离、切比雪夫距离和马氏距离等，而基于相似系数度量方法主要有余弦相似度、皮尔森相关系数、杰卡德相似系数等。其中，欧氏距离和余弦相似度的应用尤为普遍。相比于欧氏距离利用数据点的距离作为度量的依据，余弦相似度更关注向量之间的夹角，分析数据在方向上的差异。作为经典相似性度量方法，余弦相似度常用于文本处理［1］、特征选择［2］、视觉任务［3］、实例检索［4］等领域。只关注方向的特性使得余弦相似度对噪声的敏感度较低。文献［3］提出一种局部加权余弦相似度来衡量目标模板和候选模板的相似度，有效抑制脉冲噪声导致的负面影响。文献［5］在直流线路短路故障中通过余弦相似度来检测故障端子极性现象，无需考虑幅值问题，从而有良好的抗噪性能。

尽管余弦相似度在多个应用中表现出良好的效果，但由于对绝对数值不敏感，余弦相似度无法识别方向相同但模长相异的数据向量的差异，在需要度量模长的场景中准确性较差。文献［6］指出余弦相似度只关注方向差异的特点会给某些识别任务带来比较大的影响，当数据分布比较密集时，向量夹角往往趋向于零，相似度普遍较高的情况下分类器无法区分实际上不相似的模式。针对上述存在的问题，文献［7］提出一种改进余弦相似度，通过引入数据点距离的Lp范数以及正则项，使得相似度函数能兼顾数据点距离以及向量夹角两方面。文献［8］则利用数据序列的模长比值来构造相似系数进行修正。还有文献［9］使用调整余弦相似度进行度量，通过减去数据均值化原点矩为中心矩，消除各个维度的量纲差异。当前，模糊集、中智集领域中关于相似性度量的研究工作比较深入，在余弦函数和余切函数的基础上也提出了多种相似度计算公式［10-12］。但上述研究基本没有对所提方法如何解决余弦相似度的不足进行清晰的文字阐述和相关的数学推算。

除此之外，以往相似度计算需要逐一遍历数据来计算数据集之间的相似度，适用于小规模数据集，但其运算时间会随着数据集规模扩增呈指数型增长，不适合应用于大规模数据集。为了摆脱高计算成本的困扰，文献［13］认为实现高速计算的方法之一是预先将计算所需的一些统计信息存储在索引中。文献［14］通过预先选择的代表性查询图像和相似度表来评估图像的相似程度。上述研究中，减少计算时间的本质是通过预计算来减少后继的冗余计算。值得注意的是，目前相似性度量的研究中关于快速计算这一方面的文献还比较欠缺。

综上所述，本文将针对余弦相似度准确性较低这一不足以及遍历计算方法时效性差的局限性展开相关的探索和研究。提出2种余切相似度并分析其在相似性度量中的优势，阐述基于BP神经网络的相似度快速计算方法和流程，针对改进方法的实验结果进行准确性和时效性的讨论分析，并进行总结与展望。

1 余切相似度计算公式

首先通过研究余弦相似度的计算公式揭示其不足，然后提出2种余切相似度计算公式，通过数学推算和实例说明分析余切相似度在衡量数据相似度方面的优势。

1.1 余弦相似度

余弦相似度的原理是通过计算数据向量的夹角余弦来表征两者的相似程度。假设有3个数据A、B、C，其 中A=(a1，a2，...，am)，B=(b1，b2，...，bm)，C=(c1，c2，...，cm)，m(m∈N*)表示数据维数。为了方便表述，令M={i∈N*|1≤i≤m，m∈N*}表示维度索引取值范围。A与B的余弦相似度计算公式如式（1）：

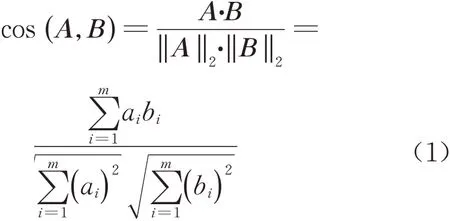
其中，‖ ·‖2表示数据向量·的二范数。数据向量夹角越大，余弦值越小，表示两者相似程度越低；夹角越小，余弦值越大，表示两者相似程度越高。式（1）表明余弦相似度实质上等于向量A、B单位化后的乘积，通过将数据点映射到单位超球面上，消除了数据模长的影响，只关注数据向量的方向。这也是余弦相似度对绝对数值（即模长差异）不敏感的原因。以m=2为例说明余弦相似度现存的问题，二维数据A、B的示意图如图1所示，其中θ表示二维向量A、B的夹角。

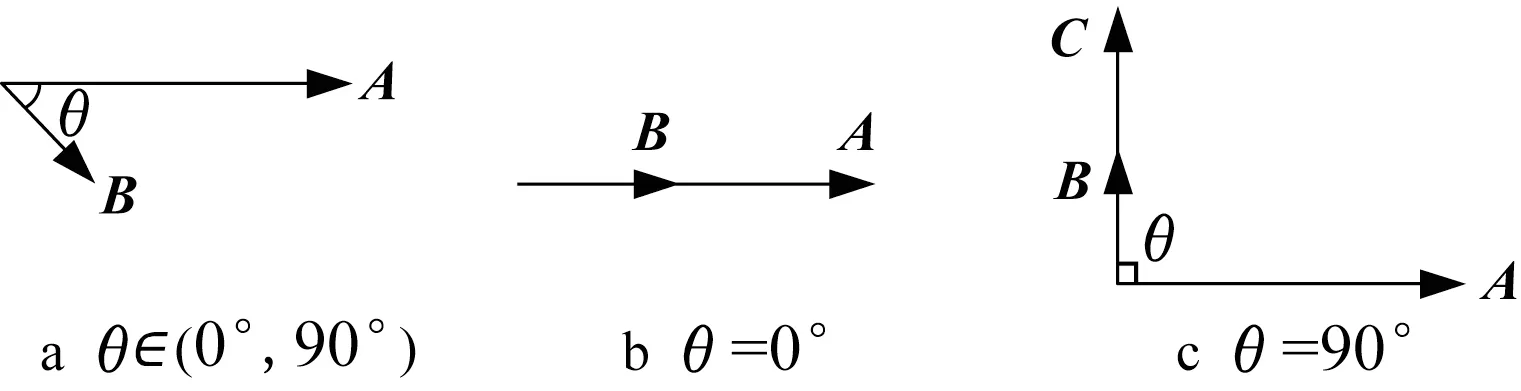
图1 二维向量关系示意图Fig.1 Schematic diagram of relationship between two-dimensional vectors

当相似度度量任务需要考虑数据模长差异的时候，式（1）仍然存在2个缺点：

（1） 假 设 A=k·B(k∈N*，k≠1)， 由cos(A，B)=1可以得到数据向量A和B方向相同即完全相似的结论。但实际如图1b所示，两者虽方向相同但模长相异，意味着余弦相似度对此无法作出准确判断。

上述问题增大了余弦相似度计算误差，无法为数据的相似度度量提供一个准确的理论依据。为了能够更加准确地评估数据集的相似程度，改进的相似度计算公式simi(A，B)必须满足以下原则：①simi(A，B)需体现出数据各个维度上的差异。②simi(A，B)∈[0，1]，并且当simi(A，B)→1，其表征数据的相似度越高；当simi(A，B)→0，其表征数据的相似度越低。③当且仅当A=B时，才有simi(A，B)=1。

1.2 余切相似度

数据的相似程度取决于各个维度之间的数值差异，针对余弦相似度的缺点以及新计算公式需遵循的原则，提出2种余切相似度计算公式，该公式侧重于计算数据各维度之间的距离。

1.2.1 两种余切相似度定义

假设数据A、B进行归一化后得到A′=(a′1，a′2，…，a′m)以 及 B′=(b′1，b′2，…，b′m)，其 中a′i，b′i∈[0，1]，i∈M，有0≤|a′i-b′i|≤1。提出的第1种余切相似度具体公式如式（2）：

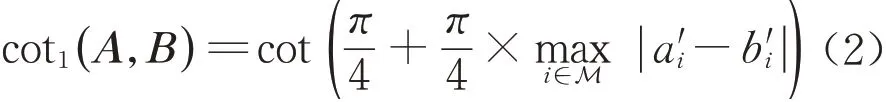
第2种余切相似度具体公式如式（3），其中k表示|a′i-b′i|≠0的个数。当k=0，表明A和B完全相似；当k≠0，说明A和B存在差异，则计算各维度差值的平均值，然后计算数据的相似度。

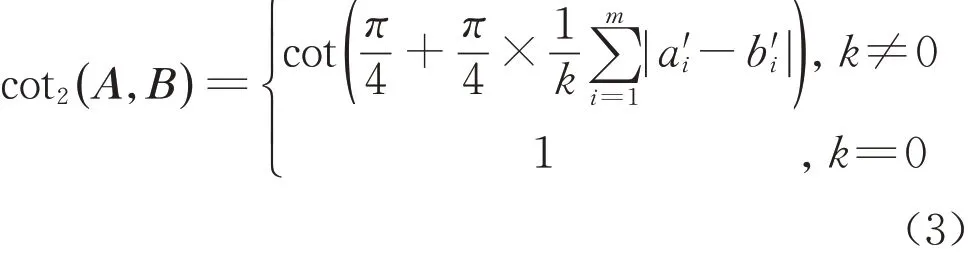
由式（2）、式（3）可知，第1种余切相似度计算公式根据数据维度差值的最大值来比较两者的相似程度，而第2种余切相似度计算公式则是基于数据维度差值的均值来比较两者的相似程度。2种余切相似度公式从2个角度来评判数据的相似程度，为数据集的相似度计算提供了全面的参考依据。

1.2.2 余切相似度分析

基于数学公式对上述2种余切相似度的有效性进行分析。

对于第2种余切相似度而言，当且仅当∀i∈M都有|a′i-b′i|=0，即k=0时，有cot2(A，B)=1，表征数据A和B完全相似；仅当，有cot2(A，B)=0，表征数据A和B完全不相似；当0＜，有cot2(A，B)∈(0，1)。

对2种余切相似度公式进行对比分析：

（1）第1种余切相似度以维度差异峰值作为判别相似度的标准，第2种余切相似度则以维度差异均值作为标准。前者希望相似样本各个维度的数值都能够尽量接近，后者则倾向于相似样本各个维度的数值整体上比较相近，不需要每个维度都十分贴近。

（2）不失一般性地，假设数据A与B只有前k(k∈M)个维度不相同，因为，所以总有cot1(A，B)≤cot2(A，B)成立。3.4节实验数据能够佐证这个特点。

综上，对比于余弦相似度，2种余切相似度能够应对数据向量方向相同模长相异的特殊情况，而具体应用哪条公式需要根据实际需求进行选择。

1.3 相似度计算实例说明

为了更清晰地呈现相似度计算过程，列举5个10维数据（已归一化）加以说明，如表1所示。

表1 5个10维数据实例Tab.1 Five instances of 10-dimensional data

根据式（1）、式（2）、式（3）计算出5个数据的相似度矩阵，如表2～表4。其中，第i行第j列数值表示第i个数据和第j个数据的相似度。由于每个数据与自身完全相等，矩阵对角线的相似度均为1。表1中，数据B在维度1、5、7的取值分别是0.321 2、0.5091、0.314 1，数据E在维度1、5、7的取值分别为0.519 0、0.613 1、0.223 5。根据表2～表4可知：cos(B，E)=0.9880，cot1(B，E)=0.7292，cot2（B，E）=0.912 0。由于B和E夹角只有8.9°，余弦相似度认为数据B和数据E的相似程度非常高；而余切相似度认为两者的相似程度不那么高，尤其是第1种余切相似度认为数据差异比较大。实际上，由于数据已进行归一化，数据B和数据E在维度1、5、7的差值都接近甚至超过0.1，意味着两者的相似程度是比较低的。该计算实例反映了余弦相似度的缺点在于其只关注向量方向差异，当向量夹角比较小时，使用余弦相似度将严重弱化数据间的差异，无法准确判别其相似程度，意味着如果应用到分类等任务中无法对数据进行正确区分。而2种余切相似度能够有效分辨数据各维度的差异，不仅能有效弥补上述不足，当数据向量夹角比较大时，依然有比较好的相似度衡量能力。

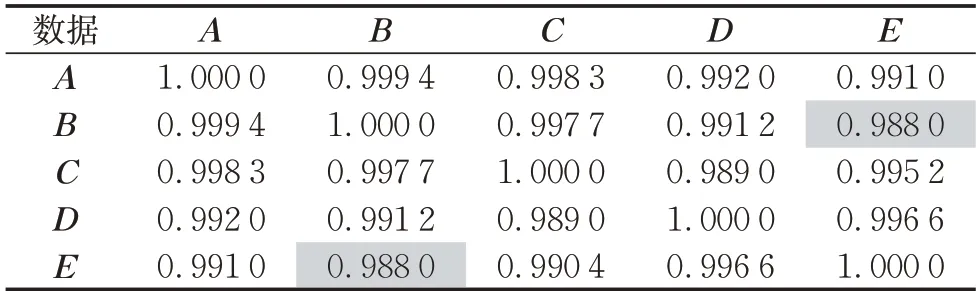
表2 余弦相似度矩阵Tab.2 Similarity matrix by cosine similarity formula

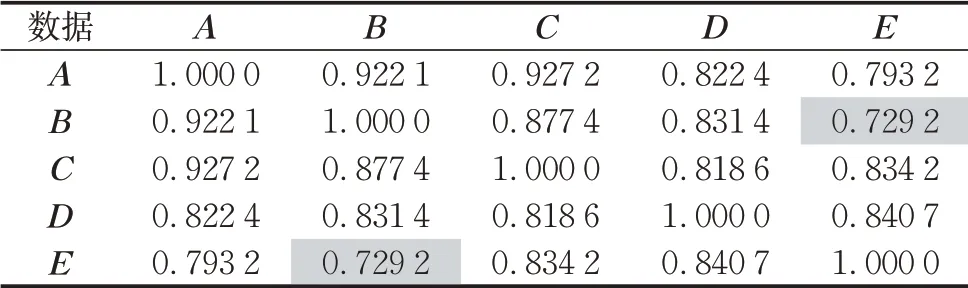
表3 第1种余切相似度矩阵Tab.3 Similarity matrix by first cotangent similarity formula

2 基于BP神经网络的相似度快速计算

传统相似度计算采用遍历方法，通过计算所有数据之间的相似度得到整个数据集的平均相似度，但面对高维数据时，存在运算时间长、内存消耗大的问题。为了提高相似度计算性能，引入BP神经网络，旨在建立一个能够拟合数据集相似度映射关系的网络模型，减少相似度计算时间。

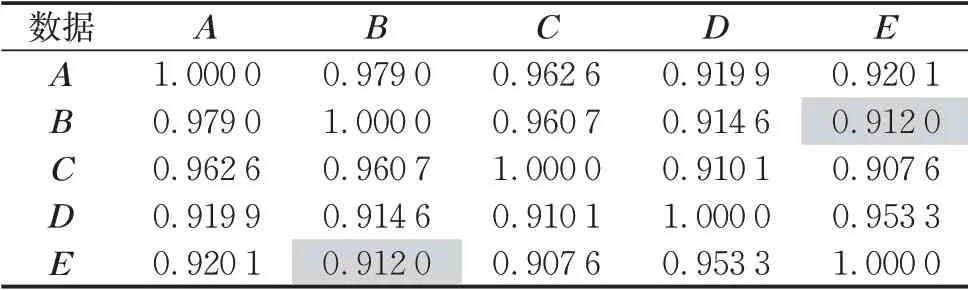
表4 第2种余切相似度矩阵Tab.4 Similarity matrix by second cotangent similarity formula

2.1 BP神经网络

BP神经网络是一种按照误差逆传播算法训练的前馈神经网络，具有比较优秀的非线性逼近、自学习、自适应和泛化能力，其应用十分广泛。根据万能逼近定理［15］可知，一个前馈神经网络如果具有线性输出层以及至少一层具有“挤压”性质激活函数的隐藏层，只要有足够多隐藏神经元，可以以任意精度逼近有限维空间内的任意连续函数。由于必须考虑计算时间与空间的开销，实际上使用的多层神经网络通常是放弃苛刻的精确表示，而是在近似表示的基础上寻找合适的参数对数据集与标签集之间的非线性映射关系进行逼近。这为使用BP神经网络进行相似度快速计算提供理论基础。

2.2 相似度快速计算实现

相似度计算公式选定之后，数据的数值与数据之间的相似度可以构成确定的多输入多输出的非线性映射关系，因此可以采用BP神经网络拟合这种映射关系。为了减少遍历计算的时间，基于部分样本的相似度对模型进行训练，用精度换速度，在误差允许范围内表征完备数据集的非线性相似度映射关系，从而计算出完备数据集的近似相似度。

基于余切相似度和BP神经网络的相似度快速计算方法主要分为4个部分：训练样本提取、训练样本相似度计算、网络模型训练以及完备数据集仿真，具体流程如图2。假设数据集P共有n个m维数据，P={p1，p2，...，pn}。为 了 简 化 表 述，令N={j∈N*|1≤j≤n，n∈N*}表示数据索引取值范围。相似度快速计算的算法伪代码如图3所示，具体步骤如下。

（1）对数据集P进行归一化处理得到P′={p′1，p′2，...，p′n}，其中p′j(j∈N )表示经过归一化后的数据集P′的第j个数据。

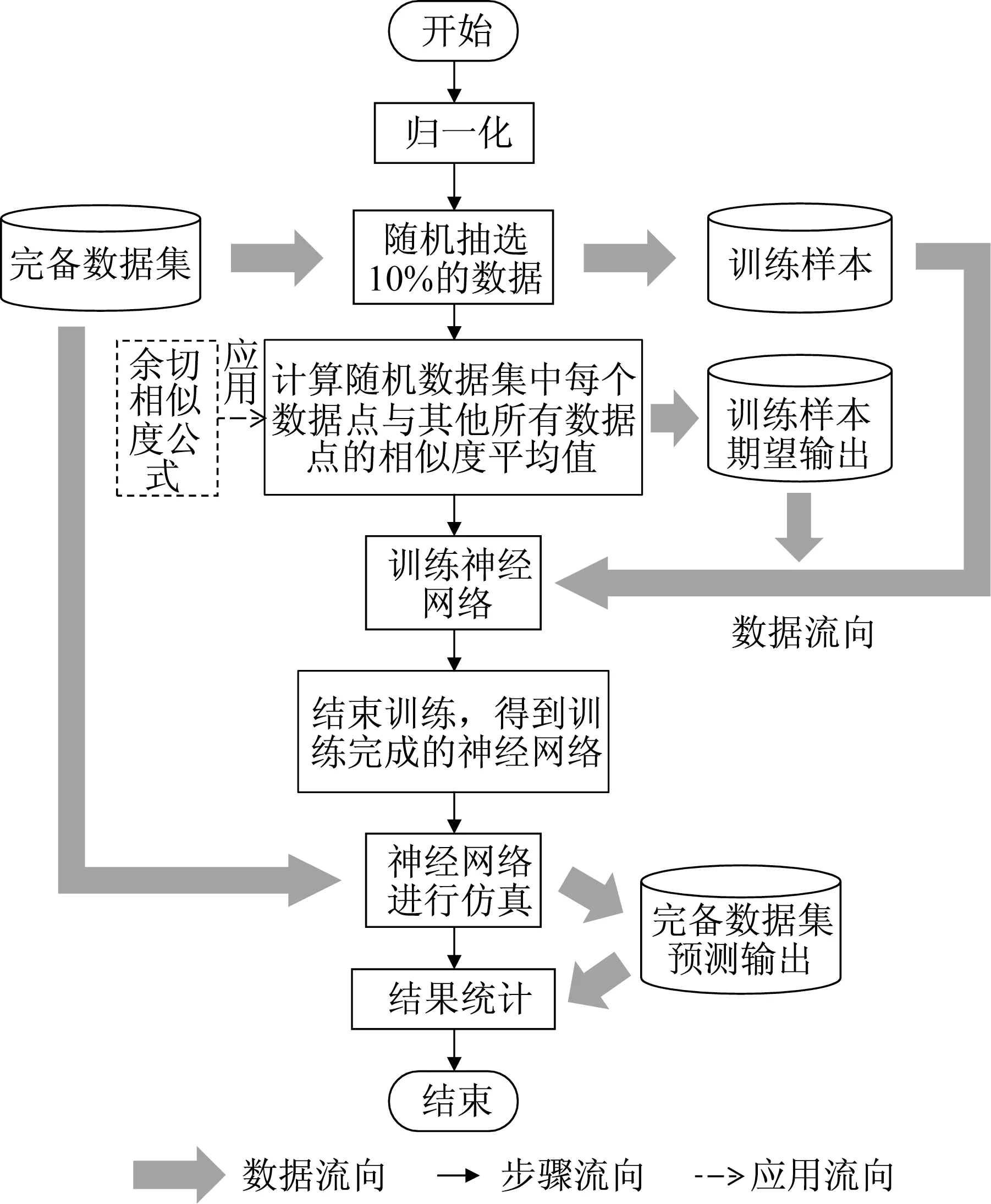
图2 基于余切相似度和BP神经网络的相似度快速计算流程Fig.2 Flowchart of fast similarity calculation based on cotangent similarity and BP neural network

（2）随机从归一化数据集P′中抽取10%的数据作为训练样本。该训练集表示为P′x={p′x1，p′x2，...，p′xk}，x1，x2，...，xk∈N。应根据数据集大小以及维数合理地调整百分比。

（3）使用余切相似度计算训练集P′x中每一个数据与其他数据的相似度的平均值，以此作为期望输出 ，设 为 Yx=(yx1，yx2，...，yxk)，其 中 yxt=(p′xt，p′j)，表示数据p′xt的平均相似度，xt∈{x1，x2，...，xk}。

（4）向初始化后的神经网络输入训练集Px′和期望输出Yx，训练网络模型，直至误差精度达到要求。

（5）将完备数据集输入训练好的网络模型进行仿真，求得所有近似平均相似度，设为Y=(y1，y2，...，yn)，其 中yj表 示 数 据p′j的 近 似 平 均 相似度。

（6）通过式（4）求所有数据的近似平均相似度的均值，得到完备数据集P的相似度。

图3 基于余切相似度和BP神经网络的相似度快速计算伪代码Fig.3 Pseudocode of fast similarity calculation based on cotangent similarity and BP neural network

2.3 快速计算复杂度分析

提出的相似度快速计算方法建立在对训练样本集进行精确的相似度遍历计算的基础上。全数据集遍历计算是一个缓慢且低效的操作：如果存在n个m维数据，计算两两数据之间的相似度共需要0.5n(n-1)次相似度计算，每次计算遍历m个维度的算法复杂度为O(m)，因此遍历计算时间复杂度为O(0.5×n(n-1)m)～O(mn2)，运算时间随着数据量的增加呈指数型增长。但是实际上，在相似度公式确定以及数据量足够的前提条件下，只需要部分数据的相似度即可拟合相似度映射关系，其余的遍历计算可谓冗余计算。换句话说，只要神经网络的参数设置合理，在误差允许的范围内，对部分数据的遍历计算可以取代对全部数据的遍历计算。

现在探讨神经网络方法的时间复杂度，分为精确计算部分和训练测试网络部分。在精确计算过程中，设b是训练集比例，0＜b＜1。bn条训练数据的平均相似度需要进行0.5bn(n-1+n-bn)=0.5bn[(2-b)n-1]次相似度计算，总时间复杂度为O(0.5bmn[(2-b)n-1])～O(mn2)，但由于数据量远少于全遍历计算，所以精确计算过程的实际耗时接近遍历计算的b倍（0＜b＜1）。在测试n个m维数据时，假设单隐层全连接神经网络的输入神经元数量为m，隐层神经元数量为t，输出神经元数量为1（输入1条m维数据，输出1个相似度），神经网络方法的时间复杂度［16］为O(n(12×1×mt+12×1×t×1))～O(mnt)，在海量高维数据中往往t≪mn。因此，当数据量大或者数据维度高时，神经网络方法在效率上优于遍历计算方法。

3 实验与讨论

首先对比2种余切相似度和余弦相似度公式的计算结果以验证余切相似度的准确性。其次，对比基于BP神经网络和基于遍历计算这2种计算方法检验前者的时效性。其中，相似度算法准确性是指该算法是否能够准确表征数据的相似程度，以相似度计算误差表征；时效性是计算给定数据集平均相似度的效率，用总运算耗时作为评价指标。实验基于MATLAB平台完成。

3.1 数据集介绍

3.1.1 UCI数据集

实验首先采用标准数据库UCI Machine Learning Repository［17-18］中的Iris、Modeling、Eledeal这3个数据集验证2种余切相似度的准确性，数据集具体信息如表5。由于Iris和Modeling数据集比较小，若只抽取10%的数据作为训练数据，很可能因为训练样本不具备表征整个数据集数据分布的能力，致使网络模型欠拟合而无法提供高精度的相似度计算结果。而且，数据维度的增加使得数据集的分布特征更加复杂。因此，这里对Iris和Modeling数据分别抽取75和150个数据作为训练样本。除了数据集规模和数据维度，在实际应用中，还需要根据实际情况和生产需求作调整。

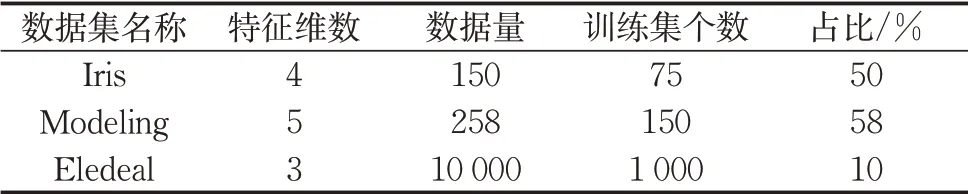
表5 UCI数据集基本信息Tab.5 Basic information of UCI datasets

3.1.2 CWRU数据集

为了探讨改进方法对于高维大数据的准确性和时效性，采用美国凯斯西储大学的轴承故障数据集［19-20］（Case Western Reserve University，CWRU数据集），将其按照不同数据量和数据维度进行切分成相应子数据集，在数据分布相似的前提下，说明和分析当数据量和数据维度增加时所得相似度误差和计算时间的变化。设CWRU-N-M表示包含N个M维数据的子数据集，例如CWRU-512-100表示512个100维数据集。实验中数据量取值512、1 024、5 120、10 240，特征维数取值100、500、1 000、2 000，共有16个子数据集。根据10%抽取训练样本原则，设定各数据量对应的训练样本数分别为100、102、512、1 024，其中为了保证模型精度，512数据量训练集比例约20%。

3.2 数据集归一化

在计算相似度之前先进行归一化处理，避免由数据度量标准不统一引起的误差。令数据集P的第j 个数据 pj=(pj，1，pj，2，…，pj，m)， 其中pj，i(i∈M，j∈N )表示数据pj的第i个维度的数值。令归一化数据集P’的第j个数据p′j=(p′j，1，p′j，2，…，p′j，m)，其中p′j，i(i∈M，j∈N )表示归一化数据p′j的第i个维度的数值。考虑到各个维度的值域范围有可能差异过大，为了保留数据的原始特征，采用min-max标准化分别对每个维度进行处理，保持数据与最小值的距离比例，计算如式（5）所示：

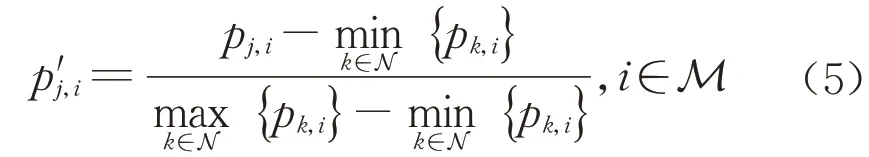
3.3 实验设置与结果

根据2.1节所述，可知具有单隐层、线性输出层以及足够多隐藏神经元的前馈神经网络能够无限逼近任意连续函数。因此在对训练时间成本和模型精度做出权衡后，实验采用单隐层全连接神经网络，模型训练的部分超参数设置如下：隐层神经元个数为10，学习率为0.01，迭代停止精度为0.000 1，最大迭代次数分别为500次（UCI数据集）和1 000 000次（CWRU数据集）。准确性实验验证结果如表6和图4，时效性实验验证结果如表7。为了简化表述，下文图表使用cos、cot1、cot2分别表示基于余弦相似度、2种余切相似度的实验结果。

3.4 准确性分析

算法准确性的验证对于不同规模的数据集都有重要意义，而且确保算法的准确性是分析其时效性的前提。基于表6和图4对UCI数据集和CWRU数据集2次实验的准确性进行分析验证。

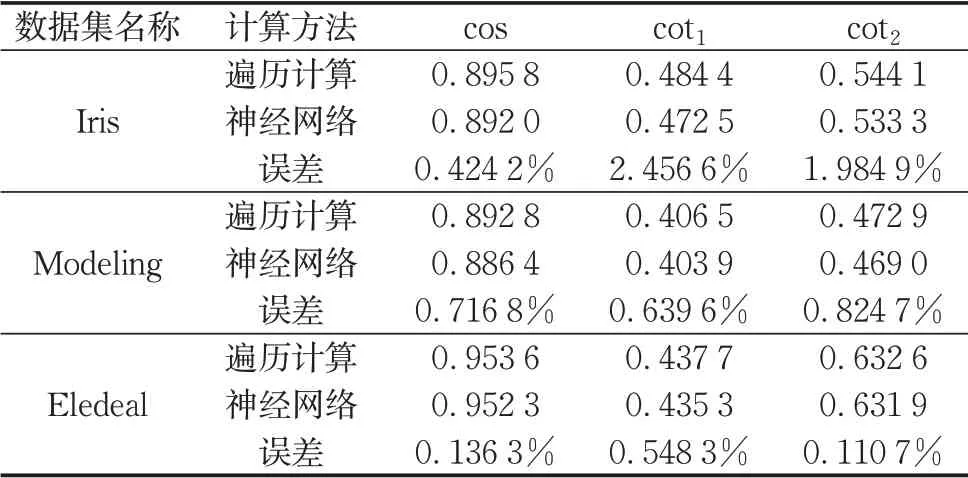
表6 基于神经网络和遍历计算的相似度计算结果（UCI数据集）Tab.6 Similarity calculation results based on BPnetwork and traversal method（UCI datasets）

3.4.1 相似度公式差异分析

以表6中Iris数据集为例，cos(PIris)=0.8958，cot1(PIris)=0.484 4，cot2(PIris)=0.544 1，显然余弦相似度判定数据走向趋势相近，过高估计了该数据集的平均相似度，因而准确性比较差；而余切相似度从维度上判别Iris数据集的差异比较大，其平均相似度比较低。不难发现，表6中3个数据集都有cot1(P)＜cot2(P)（P表示数据集名称），这是由于第1种余切相似度侧重于比较数据维度差异的峰值，第2种余切相似度倾向于比较数据维度差异的均值。

在相同数据集的情况下，前者的计算值总是不超过后者的计算值。

图4是以遍历计算的相似度为基准2种计算方法之间的相似度误差。第1种余切相似度具有最大的计算误差，而余弦相似度和第2种余切相似度的计算误差比较小，这是由于第1种余切相似度使用max函数，拟合难度相对较大，但可通过调整模型超参数进一步提升。

3.4.2 计算方法差异分析

表6中Iris数据集基于遍历计算和基于神经网络的余弦相似度误差为0.424 2%，第1种余切相似度误差为2.456 6%，第2种余切相似度误差为1.984 9%。总体来说计算误差都比较小，均在容许范围内。这很好地说明了网络模型能够较好拟合训练样本的相似度映射关系，并且具备一定的泛化能力，对完备数据集的输入具有良好的鲁棒性。图4中2种计算方法在CWRU数据集的计算误差都小于4%，对于大部分应用场景均在误差允许范围内，说明在高维数据集中，神经网络方法依然保有足够的准确度，为后文的时效性分析提供前提条件。综上所述，基于余切相似度和BP神经网络的相似度计算方法应用在数据集相似度评估中具有令人满意的准确性。

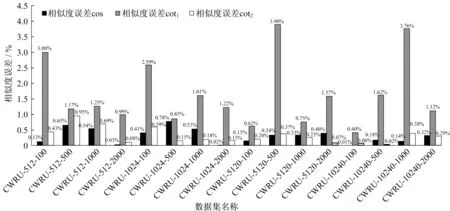
图4 基于神经网络和遍历计算的相似度计算误差（CWRU子数据集）Fig.4 Similarity calculation error based on neural network and traversal calculation(CWRU subdatasets)

3.5 时效性分析

一般来说，计算量少时不同算法之间的效率差异比较小，运算复杂度大的算法或程序才更有统计耗时的必要。由于CWRU数据集的“大规模”、“高维”特性相比于UCI数据集更加明显，因此着重分析改进方法在CWRU数据集的时效性能。为了更清晰地对比分析基于不同计算公式以及基于不同计算方法的相似度计算效率，将表7数据依据不同相似度公式以及依据不同的计算方法分别绘制相关趋势图像，如图5、6所示，注意纵坐标均经过对数缩放操作。

3.5.1 相似度公式差异分析

参照表7和图5，CWRU-512-100子数据集在遍历计算的基础上3种相似度的耗时分别为0.184 8s、0.077 4s、0.189 8s，由于数据量和特征维数相对其他子数据集而言较低，运算效率差异比较小。但随着数据维度和数据量的增长，差异逐渐显现：

（1）如果数据量固定为512，当特征维数从100增长到2 000时，大体上呈现出余弦相似度的计算时间最长、第2种余切相似度次之、第1种余切相似度最短的规律。

（2）如果特征维数固定为100，当数据量从512增长到10 240时，同样呈现出第（1）点所述规律。

而在神经网络方法的基础上，当数据量和特征维数比较少时，不同相似度在运算效率上没有绝对的优劣。根据表7，CWRU-512-100这3种相似度耗时分别为0.517 7s、0.973 6s、0.247 6s，CWRU-512-500则是0.389 0s、1.708 0s、0.480 2s，此时3种相似度公式还没有必然的大小关系。由于训练样本少，因此遍历计算部分少，此时主要由神经网络的训练决定运算时间。当数据量和特征维数增大时，遍历计算部分逐渐主导运算时间的长短。表7中，当数据量达到1 024及以上，神经网络方法的运算时间同样呈现出余弦相似度耗时最长、第2种余切相似度次之、第1种余切相似度最短的规律。

上述现象是由于余弦相似度计算了2次L2范数，时间复杂度最大；第2种余切相似度因比第1种余切相似度多1个统计非零维数步骤，运算速度相对较慢。总体而言，无论是基于遍历计算还是基于神经网络方法，2种余切相似度较余弦相似度都有一定的时效优势，尤其是针对海量高维数据。

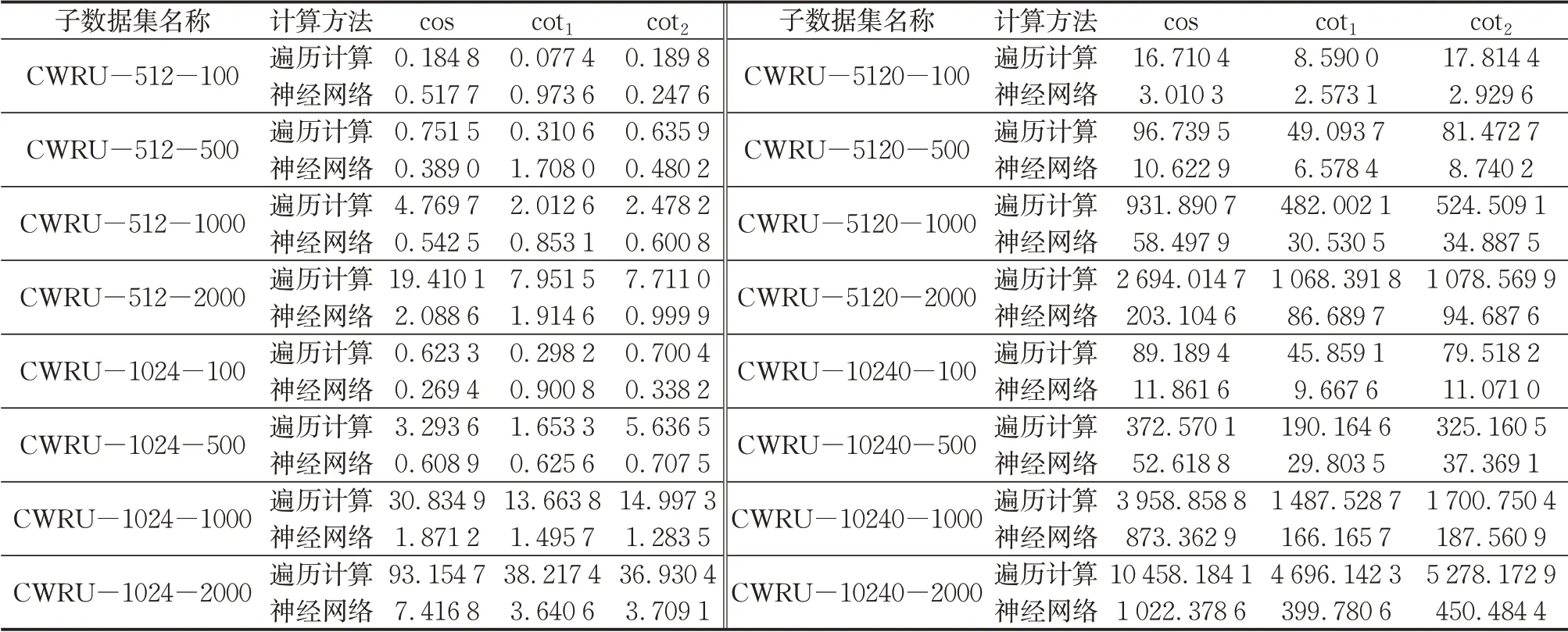
表7 基于神经网络和遍历计算的相似度计算时间（CWRU子数据集）Tab.7 Running time of similarity calculation based on neural network and traversal calculation(CWRU subdatasets) s

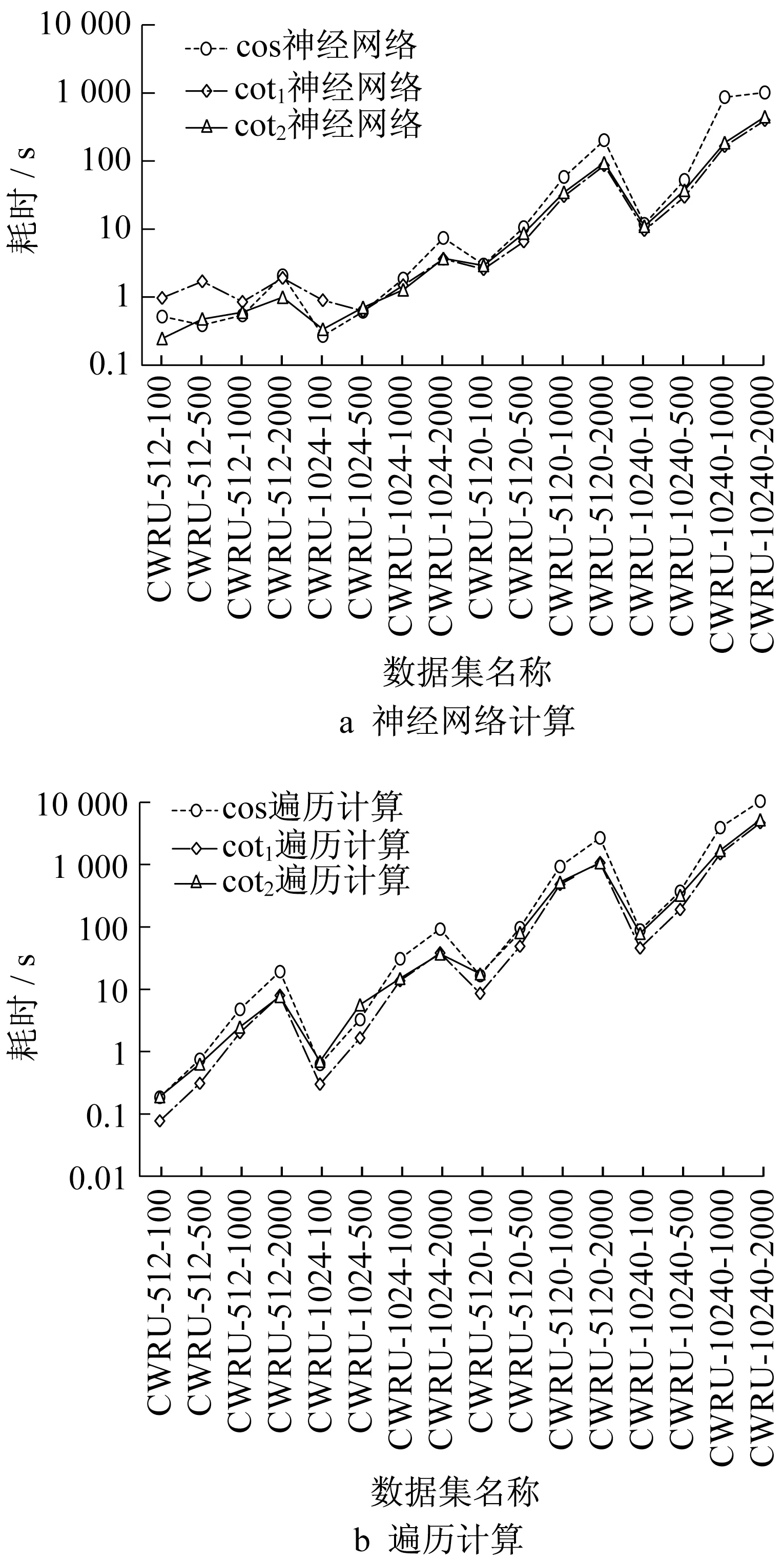
图5 基于不同计算公式的相似度计算时间对比Fig.5 Comparison of running time of similarity calculation based on different calculation formulas

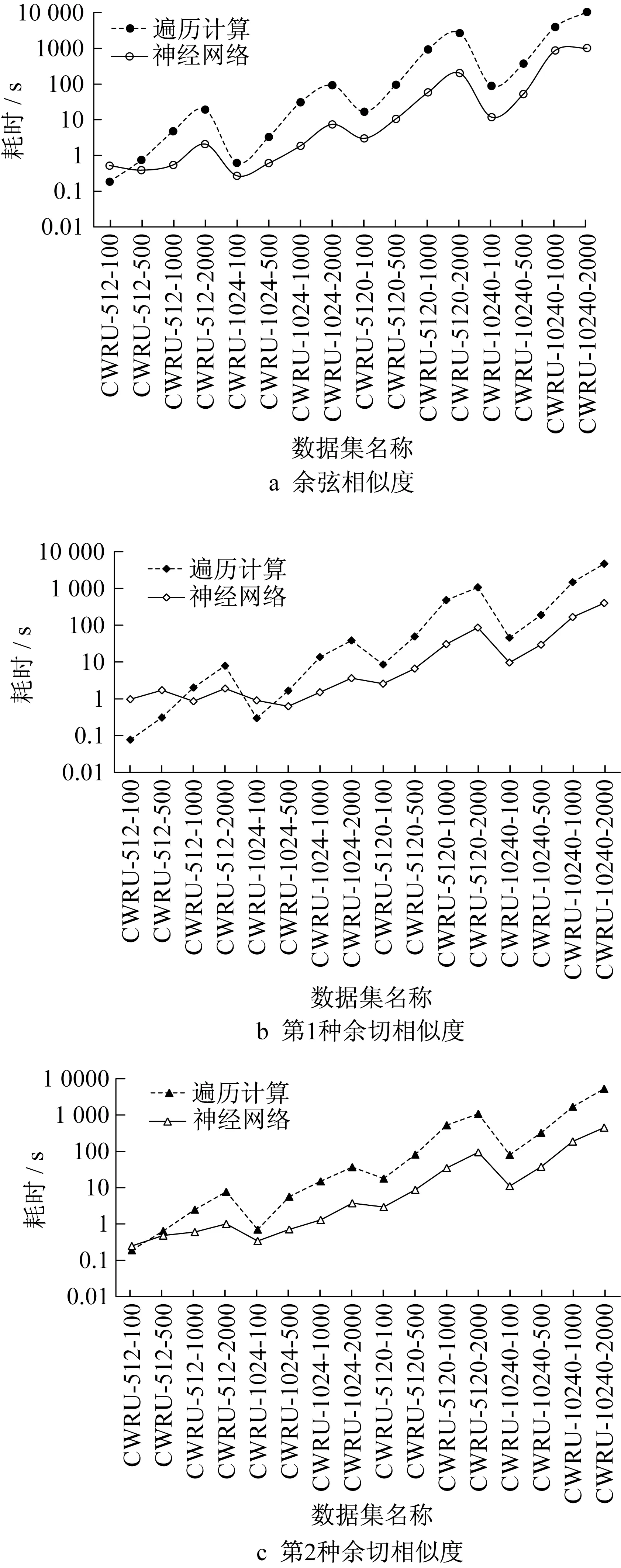
图6 基于不同计算方法的相似度计算时间对比Fig.6 Comparison of running time of similarity calculation based on different calculation methods

3.5.2 计算方法差异分析

参照表7和图6，当数据量和维数比较小的情况下，遍历计算的速度比神经网络方法要快但相差不大。以第1种余切相似度为例，表7中CWRU-512-100基于遍历计算的耗时0.077 4s比神经网络方法0.973 7s略少。随着数据集规模的扩大，遍历计算的耗时开始超过神经网络方法，其增长速度也远远高于后者，如CWRU-5120-100的遍历计算耗时8.590 0s，是神经网络耗时2.573 1s的3倍多，相对于CWRU-512-100，前者增长了100多倍，后者仅增长了2倍多。由于工业大数据的数据量一般都十分庞大，可以预想，当数据量和维数继续增加到一定程度时，遍历计算将因为巨大的空间和时间代价而无法继续直接计算，而此时神经网络方法的计算成本依然能被接受。因此，神经网络方法有效提高了相似度计算效率，在评估大规模数据集相似度时比遍历计算方法更加适用。

根据上述分析，相比于遍历计算，神经网络计算方法在时效性方面有了很大的提升，更适用在大数据相似度评估工作中。至此，基于BP神经网络的相似度快速计算方法的时效性得以验证。

4 结语

从大数据相似度评估工作切入，针对余弦相似度准确性较差、遍历计算方法时间复杂度大的问题，提出了2种余切相似度公式以及基于BP神经网络的相似度快速计算方法，并基于Iris等经典数据集进行验证。实验证明，改进相似度计算方法在面对小规模低维数据集和海量高维数据集时都能保持良好的准确性和时效性。作为对传统余弦相似度计算方法的一种改进和补充，本文提出的余切相似度快速计算方法既能改善传统余弦相似度只关注数据向量夹角而忽略模长的局限性，又在大规模高维数据集相似度计算方面表现出较好的适应性。

提出的改进相似度计算方法主要应用于结构化数据，因此未来的研究工作应该对非结构化数据和半结构化数据提出更加有针对性的相似度度量方法。其次，改进算法针对以二维数组描述的数据集，但不适用于以树、链表等复杂数据结构表达的数据集，今后的工作会考虑向复杂数据结构的相似度度量领域开展。最后，可以考虑引入卷积神经网络等深度学习方法进行计算，进一步提高算法的运算效率。

作者贡献申明：

乔 非：研究工作的思路与全程指导。

关柳恩：研究工作的完善与总结。

王巧玲：初步的研究工作。