考虑疲劳均衡的海上风电场主动尾流控制研究

王 俊， 周 川， 蔡彦枫， 邓智文， 许 昌

（1.中国能源建设集团 广东省电力设计研究院有限公司， 广东 广州 510663； 2.广东科诺勘测工程有限公司，广东 广州 510663； 3.河海大学 能源与电气学院， 江苏 南京 211100）

0 引言

随着风电产业的高速发展，陆上风电开发日趋饱和。 海上风资源优越、环境影响小，开发海上风电成为风电产业的趋势。 由于海上风电场址范围有限， 新开发的海上风电场内机组之间的排列距离逐渐缩短。 尾流效应在大型海上风电场中对风电机组输出功率产生的影响也逐渐明显，尾流效应不但会降低风电场的发电量，还会增加风电场内机组的疲劳载荷， 造成疲劳损伤和疲劳破坏， 使得风电场的故障概率及维护成本增加。

目前, 风电场中机组大多以追求自身最大发电功率为主要控制目标。然而，这种传统控制方式，忽略了尾流效应对其他风电机组的影响，只能实现单台风电机组的输出功率最大， 使风电场中上游机组捕获较多的风能， 而下游的机组捕获风能大大减少， 从而无法达到整场的输出功率最优。同时，风电场内各机组间疲劳载荷差异化增加，给运维带来难度。 考虑尾流影响，进行风电场主动尾流控制可以平衡各机组之间的疲劳载荷。

近年来， 考虑风电场疲劳载荷的综合优化越来越引起学者的注意。 Spudi V[1]基于Sim Wind Farm 风电场仿真平台软件，提出了一种减少风电场内各台机组载荷均方差的优化方法，通过降低风电场内机组的临时检修次数来减少临时维护量，提高经济效益。 M Soleimanzadeh[2]提出了一种风电场控制器， 可同时优化机组的功率和载荷，在低风速时调节机组转速信号，高风速时调节机组的俯仰角信号， 但没有考虑到机组控制器与风电场控制器之间的相互作用。Hart E[3]利用Bladed 软件分别对2 MW 和5 MW风电机组仿真，根据不同的湍流强度、风剪切指数和平均风速，基于模拟数据建立查寻表进行风电机组的疲劳分析。Yang J[4]提出一种减少风电场风电机组部件疲劳载荷的方法， 针对机组的叶片、轮毂、偏航和塔架的3 个方向，根据核密度函数分析其疲劳载荷， 并建立疲劳载荷数据模型找出平均风速、 湍流强度和有功功率对机组疲劳载荷的影响。Zhao R[5]提出一种基于智能代理理论优化大型海上风电场机组疲劳分布方法。Laursen T K[6]提出一种风电场模型预测控制器来实现风电场的尾流效应最小化。 Reyes H M[7]构造一种包括风电机组各重要部件载荷的多维查寻表，利用内插法，能够较好地预测处于风电场主动尾流控制下风电机组的载荷趋势。 目前关于风电场疲劳均衡的研究通常为给定电网调度指令情况下， 通过机组功率调控风电场疲劳载荷差异最小化， 没有考虑风电场功率提升和疲劳平衡的综合优化。

本文的尾流优化控制综合考虑了海上风电场疲劳均衡和发电量提升，分别采用基于桨距角的主动尾流控制和基于偏航角的主动尾流控制方法，引入量子粒子群算法为优化算法，建立考虑疲劳均衡的海上风电场主动尾流控制优化模型。

1 机组疲劳损伤计算

本文以某2 MW 风电机组为研究对象， 基于风机性能分析和GH-Bladed 软件来计算风电机组的载荷。

1.1 最大功率追踪控制工况下载荷计算

综合叶片根部、轮毂中心和塔架底部各关键零部件疲劳损伤量， 可以得到该2 MW 风电机组在最大功率追踪控制时，不同风速下的疲劳损伤量数据库，如表1 所示。

表1 最大功率追踪控制工况下的风电机组疲劳损伤量Table 1 Fatigue damage of wind turbine under maximum power tracking control

1.2 风电机组桨距角控制工况下载荷计算

目前， 风电场主动尾流控制 （Active wake control，AWC）的方法主要分为两种：一种是基于轴向诱导因子的控制方法，通过控制机组轴向诱导因子来降低尾流风速的减损；另一种是基于偏航角的控制方法，通过调节机组偏航角改变其尾流的方向，来减小尾流效应的影响。 对于前者，本文取风电机组的桨距角β 作为控制参数，以便于在Bladed 软件中进行相关载荷计算。

根据该2 MW 风电机组风速-功率曲线，分别将风电机组的叶片β 设置为-2，1，4，7，10，13 °，并对应每个β 下设置4，6，8，10 ，12 m/s 5 个计算风速。 基于GH-Bladed 软件进行机组疲劳载荷计算，建立不同风速和不同β 下的疲劳损伤数据库。以β=4°为例，结果如表2 所示。

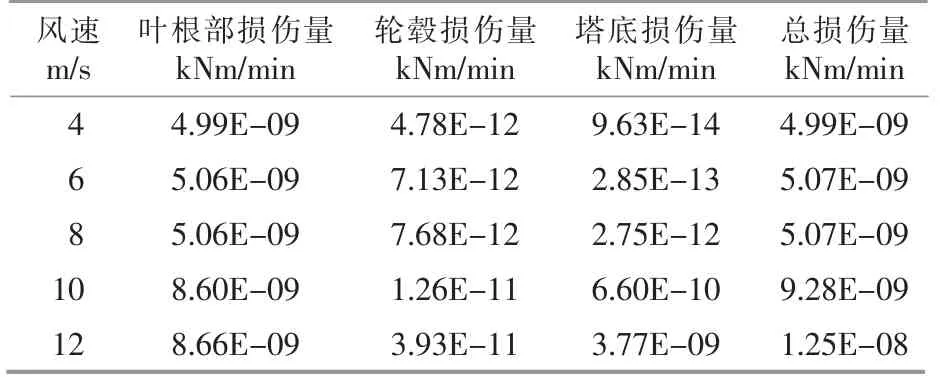
表2 β=4°时，控制运行风电机组疲劳损伤量Table 2 Fatigue damage of wind turbine controlled by pitch angle β=4°

1.3 风电机组偏航角控制工况下载荷计算

机组通过偏航改变尾流方向的同时， 其自身所受疲劳载荷也发生了变化。 本文基于GHBladed 软件，通过改变入流风的风向来模拟机组的偏航角度。 以偏航角0～45°（以5°为间隔），风速4～24 m/s（以2 m/s 为间隔）为区间，进行机组疲劳载荷计算， 建立机组不同风速和偏航角下的疲劳损伤数据库。 以偏航角15°为例，结果如表3所示。

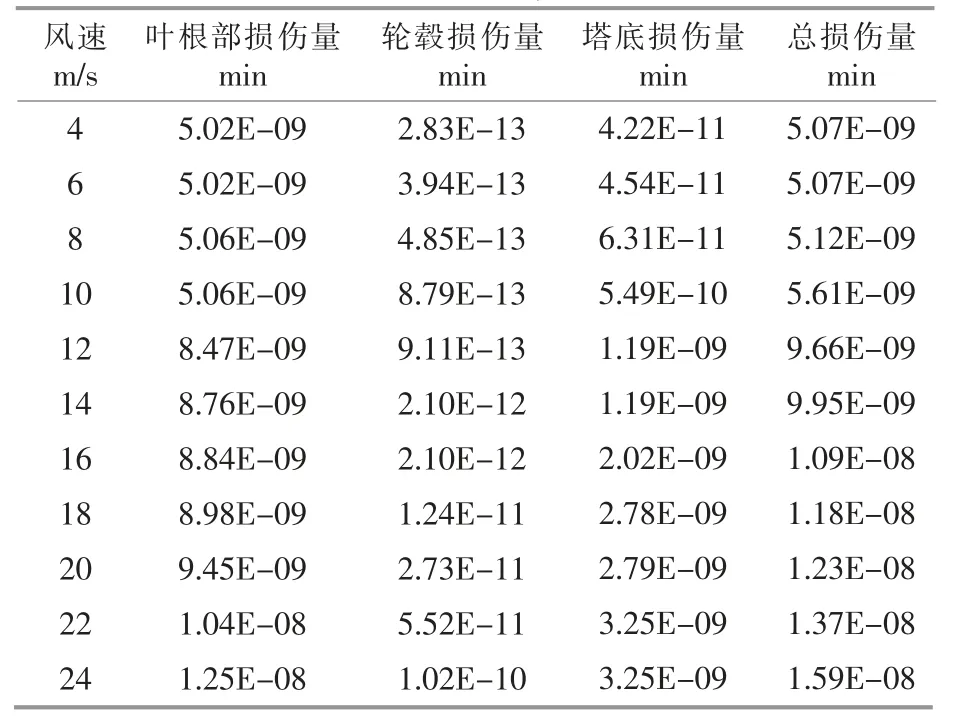
表3 主动偏航15°运行疲劳损伤量计算结果Table 3 Fatigue damage calculation results of 15 ° operation with active yaw

2 尾流计算

本文采用的尾流计算方法来自文献[8]，在计算基于轴向诱导因子的尾流调控时， 采用Jensen尾流模型进行计算。 当机组偏航角偏离对风方向时，会导致尾流风向产生偏移，如图1 所示。图中，θ 和θL分别为风向方位角以及两机组机位之间的夹角。

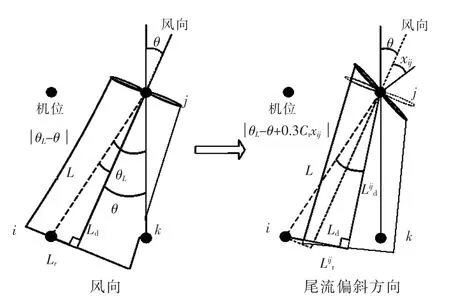
图1 机组尾流偏斜Fig.1 Wind turbine wake deflection

当机组j 的偏航角为xij， 导致尾流中心线产生了0.3 CTxij的偏移角度，机组i 在机组j 尾流中的轴向距离Ld和径向距离Lr也随之发生改变，偏移后的Ld和Lr与xij之间的函数关系为

偏航工况下机组输出功率与xij关系为

式中：Pyaw为偏航工况下机组输出功率；P 为最大风功率追踪下输出功率。

3 基于量子粒子群的风电场疲劳均衡主动尾流控制优化模型

3.1 目标函数和约束条件

3.1.1 目标函数

为减小风电场的疲劳损伤量， 均衡各台机组的疲劳损伤， 本文选择优化风电场内疲劳损伤量最大的风电机组，得到的优化目标表达式为

式中：i 为机组编号；N 为风电场内机组个数；FT为周期T 内风电场中最大的风电机组疲劳损伤量。

由于1 min 内疲劳损伤值数量级较小， 为方便后续计算乘以比例因子k，k=109。

②风电场整体输出功率目标

在电网不限制风电场发电量的情况下， 一方面降低风电机组之间的疲劳损伤差异， 另一方面还要提升风电场整体发电量，得到功率优化目标为

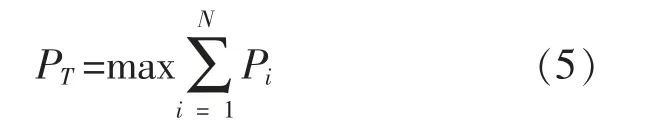
式中：PT为T 周期风电场总体发电量。

综上可得， 风电场主动尾流控制优化的多目标函数表达式为[9]

式中：λ 为常数，表示风电场内机组疲劳损伤量相对整体输出功率的重要程度。

3.1.2 约束条件

β 上下限约束为

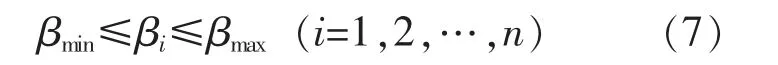
在Bladed 仿真软件或风电机组实际运行过程中， 实际风能利用系数Cp的值为0.2～0.45，本文选取机组的最佳叶尖速比为8.4，β 的最大值和最小值分别取10°和-2°。

偏航角控制约束为

偏航角最大值和最小值分别设定为45 °和0°[10]。

3.2 优化算法

标准粒子群优化算数学描述如下： 假设在一个D 维的决策空间中，种群规模为M，其中粒子i在t 时刻的位置可表示Xi=（xi1，xi2，…，xiD），i=1，2，…，M。粒子i 的“飞行”速度表示为Vi=（νi1，νi2，…，νiD）。 粒子i 在t 时刻第j 维空间中的位置和速度可根据下式进行更新：

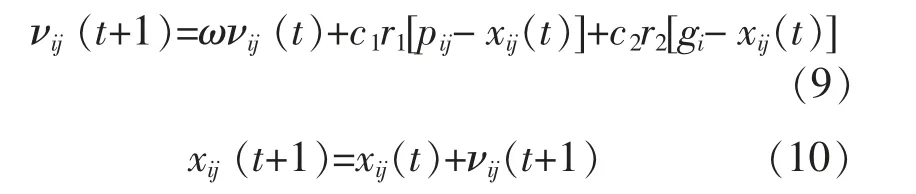
式中：ω 为惯性权值；c1，c2为学习因子，通常令c1=c2=2；νij∈[-νmax，νmax]，νmax是常数，用于限制粒子的飞行速度；r1，r2为在[0，1]内的均匀随机数；gi为全局极值；pij为个体极值。

标准粒子群算法虽然原理简单并易于操作，但粒子搜索范围受限， 不能保证以概率1 全局收敛。 量子粒子群算法 （Quantum Particle Swarm Optimization，QPSO） 将量子行为与粒子群算法相结合，不仅保留粒子群算法的一些优点，还大大提升了计算效率，具备全局收敛、控制参数少、寻优能力高的特点。 QPSO 用波函数表示粒子位置，通过蒙特卡洛方法求出，其更新方法为[11]

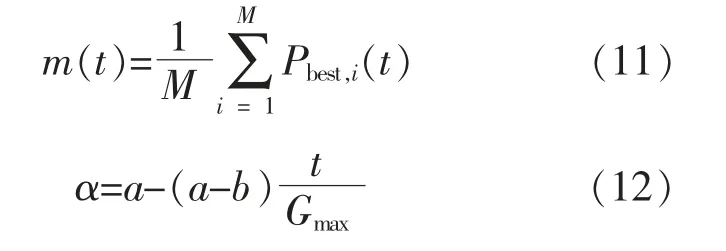
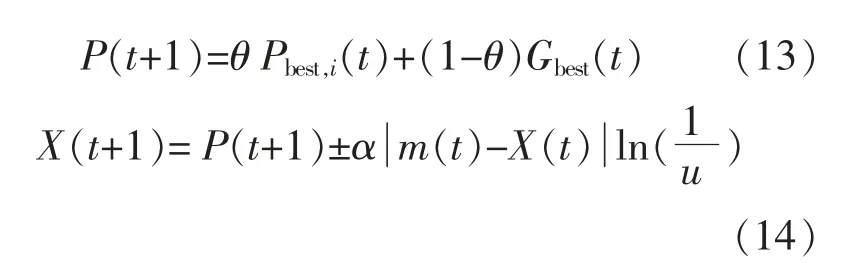
式中：Pbest，i为当前迭代中粒子i 的个体最优位置；Gbest为当前全局最优位置；θ，u 均为在[0，1]上服从均匀分布的随机数；P 为第i 个粒子位置的更新，取+和-的概率为0.5；α 为创新系数， 用于控制粒子收敛速度；a，b 为常数， 本文取a=1，b=0.5；Gmax为最大迭代次数。

QPSO 算法流程实施步骤如下。

①参数初始化：包括粒子群大小M，粒子维度D，粒子初始位置及个体最优位置。

②计算各个粒子的适应度，求出初始个体最优值、全局最优值、个体最优位置以及全局最优位置。

③根据式（13）和（14）进行粒子位置更新。

④计算位置更新后各个粒子的适应度， 并更新个体最优值和最优位置。 Pbest更新为

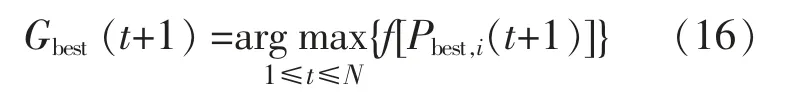
3.3 风电场优化控制方案设计

图2 为风电场的优化控制方案图。 控制器根据风电场风速预测情况， 对入流风向进行坐标变换，计算出风电场各台机组的风速，结合风电机组疲劳损伤数据库， 采用量子粒子群算法求解风电场疲劳均衡主动尾流控制优化模型， 并根据基于变桨控制的尾流调控或基于偏航控制的尾流调控分别得到并输出下一个控制周期各台机组β 或者偏航角调节控制参数。

图2 风电场优化控制方案Fig.2 Optimal control scheme of wind farm

4 算例分析

4.1 输出功率和疲劳损伤量仿真

本算例针对某海上风电场进行仿真计算，风电场的机位布置和风向如图3 所示。

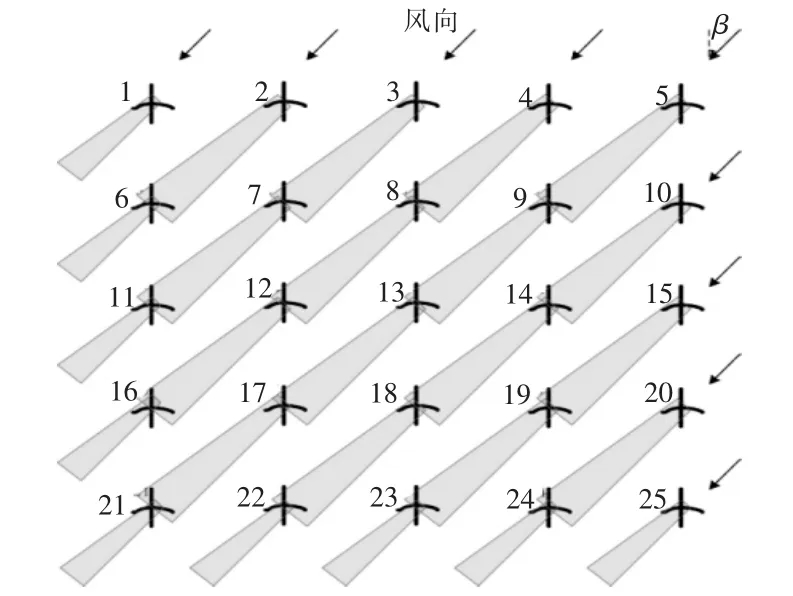
图3 风电场的机位布置和风向Fig.3 Wind turbine layout and wind direction of wind farm

该风电场共有25 台按照5×5 矩形分布的2 MW 风电机组， 机组间间距为8D （D 为风轮直径）。风电场尾流耗散系数k=0.05。本算例在自由流风速V=8 m/s，风向为正北情况下，分别采用基于β 的AWC 和基于偏航角的AWC 两种优化控制方式对风电场进行尾流优化计算。

图4 为基于传统控制各机组输出功率， 优化前的整场输出功率为8.7 MW。

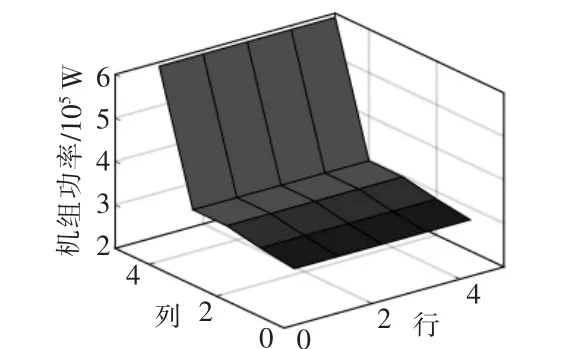
图4 基于传统控制各机组输出功率Fig.4 Wind turbine power output based on the traditional control

图5，6 分别为基于β 和偏航角的AWC 优化控制下各台机组的输出功率曲面图。

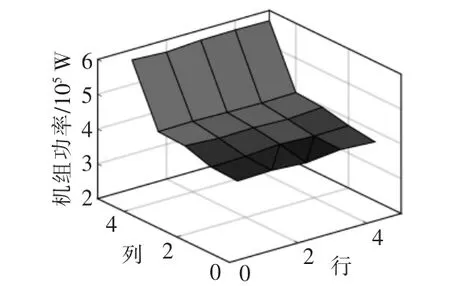
图5 基于β 的AWC 优化各机组输出功率Fig.5 Wind turbine power output based on pitch AWC

图6 基于偏航角的AWC 优化各机组输出功率Fig.6 Wind turbine power output based on yaw AWC

由图5，6 可知： 基于β 和偏航角的AWC 优化后的输出功率分别为10.6 MW 和10.1 MW；基于β 的AWC 控制下风电场各台机组的输出功率由前排往后排逐渐减小； 基于偏航角的AWC 优化下风电场各台机组的输出功率前后排没有统一的变化趋势。

图7 为基于传统控制的各机组疲劳损伤量。由图7 可知： 优化前的整场机组疲劳损伤平均值为9.00E-09，均方差为4.52E-10；基于β 的AWC优化后的整场机组疲劳损伤平均值为8.74E-09，均方差为9.43E-11； 基于偏航角的AWC 优化后的整场机组疲劳损伤平均值为1.28E-08，均方差为1.50E-10。

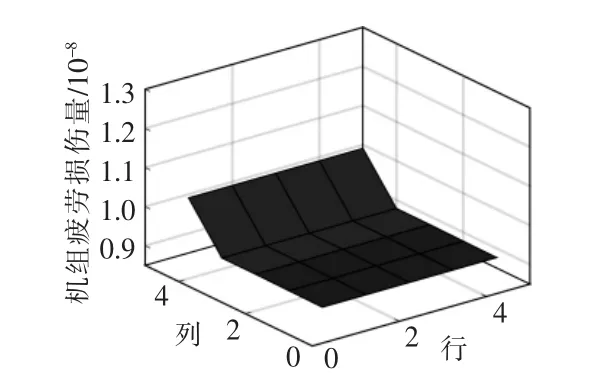
图7 基于传统控制的各机组疲劳损伤量Fig.7 Wind turbine fatigue damage based on the traditional control

图8，9 分别为基于β 和偏航角的两种AWC优化控制下， 各机组的疲劳损伤量曲面图。 由图8，9 可知：两种AWC 方式均使得风电场各台机组的疲劳差异减小，疲劳分布更均匀；基于偏航角的AWC 优化后的风电机组疲劳均量较大。

图8 基于β 的AWC 下各机组疲劳损伤量Fig.8 Wind turbine fatigue damage based on pitch AWC

图9 基于偏航角的AWC 下各机组疲劳损伤量Fig.9 Wind turbine fatigue damage based on yaw AWC

4.2 不同风向下控制策略比较

由于该风电场的分布具有对称结构， 因此对于全风向下的研究，只须讨论风向为0～90°情况，其余风向可依此类推。 依旧假设风电场输入风速为8 m/s，以每5°为风向变化步长，计算出风电场在不同控制策略下输出总功率和疲劳损伤情况。

图10，11 分别为3 种控制方法下风电场总功率和总疲劳损伤量仿真结果对比图。

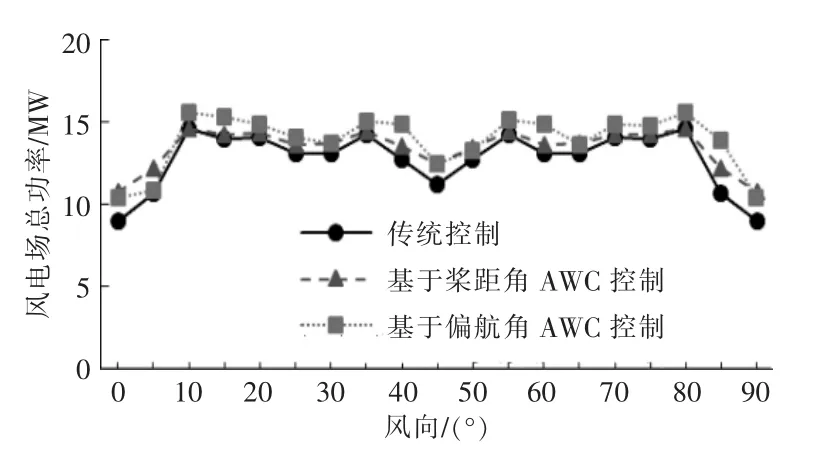
图10 风电场总功率对比Fig.10 Comparison of total power of wind farm

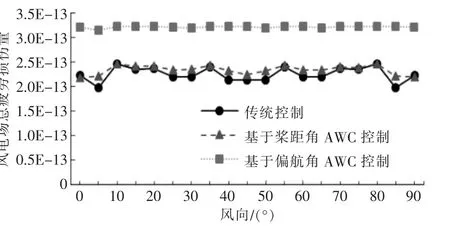
图11 风电场总疲劳损伤量对比Fig.11 Comparison of total fatigue damage of wind farm

由图10，11 可知： 风向在10～35°和55～80°时， 基于β 的AWC 优化对于风电场总功率提升效果较小，低于5%，风电场总疲劳损伤量略有提高；在其余风向下，基于β 的AWC 优化对于风电场总功率提升了5.86%～20.19%，风电场总疲劳损伤量提升幅度低于12%；基于偏航角AWC 优化，当风向在5，30，50°和65°左右时，风电场总功率提升效果较小，低于5%；在其余风向下，基于偏航角AWC 控制对于风电场总功率提升了5.34%～29.64%， 风电场总疲劳损伤量提升幅度相对较大，为31.30%～63.33%。

5 结论

针对风电场整体输出功率最大和均匀风电场机组疲劳损伤量的优化目标，本文首先基于GHBladed 软件计算建立了风电机组在不同控制工况下关键零部件的疲劳损伤量数据库， 包括最大功率追踪控制、 桨距控制和偏航控制3 种控制工况。然后结合风电场尾流风速计算方法，提出了两种海上风电场AWC 方法， 并引入量子粒子群算法进行优化求解。 仿真结果表明，两种AWC 优化策略对应风电场的总功率均有所提高， 且能够较好地平衡风电场疲劳分布。 其中， 基于偏航角AWC 优化策略的风电场总功率提升和疲劳分布优化效果更为理想， 但会造成风电场总疲劳损伤量的增大。