转向盘动力吸振器稳健性设计研究与应用

2021-02-26郭一鸣曾广劲陈守义上官文斌

振动与冲击 2021年4期

郭一鸣，曾广劲，陈守义，上官文斌

(1.湖北汽车工业学院汽车工程学院，湖北十堰 442002； 2.柳州日高汽车减振技术有限责任公司，广西柳州 545000;3.华南理工大学机械与汽车工程学院，广州 510640)

车辆共振往往是由于汽车零部件共振引起的，附加动力吸振器(dynamic vibration absorber， DVA)能有效地解决车辆振动大的问题。目前DVA已广泛应用于解决汽车振动问题，例如用于驱动桥[1-2]、转向盘[3-4]、副车架[5-6]、变速箱支撑横梁[7]等等。

汽车类DVA在设计时，一般通过DVA安装点的频响函数确定主系统的模态参数(阻尼比、固有频率);通过附加质量法确定模态质量[8]；建立模型时，一般忽略主系统的阻尼比，把DVA和主系统看作一个两自由度振动系统,以主系统与DVA质量比、主系统与DVA频率比、DVA阻尼比为设计变量，以振动放大系数最大值最小为优化目标，运用PQ定点理论进行参数优化[9]。实际上，DVA的固有频率、阻尼比、质量由于生产制造、测试等原因而存在不确定性，使减振效果达不到预期。例如，由供应商提供的橡胶阻尼式DVA的固有频率、阻尼比、质量与理论值存在5%的误差。目前，在已发表的论文中，还没有在考虑DVA的不确定性参数(DVA固有频率、阻尼比、质量)的情况下，对其减振性能进行6sigma稳健优化设计研究[10-11]。

针对某国产商用车怠速时(发动机转速在700 r/min左右)转向盘振动大的问题，用最小二乘迭代法拟合DVA安装点处的频响函数，从而识别出DVA安装位置的模态参数(安装位置处主系统固有频率、阻尼比、等效质量)；以振动放大系数最大值最小、减振效果最好为优化目标，进行基于6sigma DVA多目标稳健性参数优化设计，在制作DVA样件前，对其固有频率进行有限元仿真预测，并与实测值做对比验证；最后进行装车试验。涉及了DVA开发的整个流程，对转向盘振动控制和汽车类DVA的开发具有指导和借鉴意义。

1 转向盘振动问题分析

本文所研究的对象为某四冲程商用车，怠速时，当发动机的转速在700 r/min左右时，对应的点火频率约为23 Hz，已知转向盘的一阶模态固有频率在23 Hz左右，发动机点火频率与转向盘一阶模态耦合造成转向盘共振。对转向盘振动进行整车试验，分析该车转向盘振动问题。试验的工况为变速箱挂空挡，发动机转速为0～1 200 r/min。从振动测试结果图1可以看出，转速在676 r/min，对应频率22.5 Hz时，转向盘Y向振动较大，为解决此问题，提出了设计转向盘DVA这一方案。

图1 测试结果瀑布图Fig.1 Test result waterfall chart

2 DVA安装点处模态参数识别

设计DVA前需要获取DVA安装点处模态参数(固有频率、等效质量以及阻尼比)，频响函数拟合识别模态参数的方法已经广泛应用，通过曲线拟合方法拟合DVA安装点处的频响函数即可得到DVA安装点处模态参数。本文采用基于最小二乘迭代法的曲线拟合方法来识别DVA安装点处模态参数。

DVA安装点处的加速度频响函数可表达为

(1)

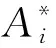
Ai=Ui+jVi
si=σi+jωdi

(2)

式中：Ui，Vi分别为Ai实部和虚部；σi，ωdi分别为si实部和虚部

待识别的参数所构成的向量为

{β}4N×1=[U1,V1,σ1,ωd1,…,UN,VN,σN,ωdN]

(3)

(4)

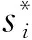
(5)

模态质量可以通过留数得到，设传递函数H(s)的第i阶留数为Ai，则第i阶的模态质量Mi为

(6)

首先，基于最小二乘法原理编写Matlab曲线拟合程序。然后，对转向盘进行模态试验，测出转向盘DVA安装点处加速度频响函数实部和虚部数据，测试时监控锤击力数值(本文的锤击力30 N),将数据的单位从g·N-1转成m·s-2。接着，选取要拟合的数据范围，拟合得到的加速度频响函数实部和虚部数据，求出加速度频响函数的极点和留数。最后，基于极点和留数，根据式(4)～式(6)算出转向盘DVA安装点处模态参数。本文选取20～25 Hz为拟合段，拟合结果如图2所示，拟合出的DVA安装处等效质量为5.77 kg，固有频率为22.4 Hz，阻尼比为0.018。

图2 加速度频响函数拟合结果Fig.2 Acceleration frequency response function fitting result

3 DVA设计

3.1 DVA原理

图3为DVA模型，图中M和m分别为主系统和DVA质量；c1和c2分别为主系统和DVA阻尼；k1和k2分别为主系统和DVA刚度；x1和x2分别为主系统和DVA位移；F(t)为主系统的激振力。

图3 DVA模型Fig.3 Dynamic vibration absorber model

定义主系统固有频率ωn1和DVA固有频率ωn2及它们的比值f分别为

(7)

定义主系统阻尼比ζ1、DVA阻尼比ζ2、质量比μ、激励频率比λ分别为

(8)

式中，ω为激励频率。

主系统位移的动力放大系数H(λ)[13-14]为

(9)

其中，

A2=(f2-λ2)2

B2=(2ζ2λf)2

C2=(f2-(f2+1+μf2+4ζ1ζ2f)λ2+λ4)2

D2=[2f(fζ1+ζ2)λ-2(fζ2+ζ1+fμζ2)λ3]2

(10)

如果主系统没有安装DVA，则其动力放大系数H′(λ)为

(11)

定义减振效果P为

(12)

3.2 DVA多目标确定性优化设计

在设计DVA时，同时考虑振动放大系数和减振效果，以振动放大系数最大值最小、减振效果最好为优化目标。考虑到安装空间，质量块范围设为0.3～0.5 kg；考虑到实际生产时橡胶阻尼比比较难调，先生产出几个样件，运用半功率法算出其阻尼比，从而确定阻尼比的设计范围，阻尼比的范围设为0.05～0.07。多目标优化模型为

(13)

式中，fn2为DVA固有频率，Hz。

fn2=ωn2/2π

(14)

采用多目标粒子群算法对DVA进行确定性优化设计，粒子群算法参数设置如表1所示,确定性优化结果如表2所示

表1 粒子群算法参数设置Tab.1 Parameter settings of particle swarm optimization

表2 确定性优化结果Tab.2 Deterministic optimization results

3.3 对确定性优化设计进行6sigma稳健性分析

从表2可以看出，振动放大系数最大值Hmax非常接近约束边界，如果设计参数存在不确定性干扰，该设计方案极有可能违反约束边界。而实际上由供应商提供的橡胶阻尼式DVA的固有频率、阻尼比、质量与理论值存在5%的误差。因此，有必要对DVA振动放大系数最大值和减振效果进行6sigma分析，评估该设计方案的稳健性和可靠性。6sigma稳健性分析的关键在于统计目标和约束的统计特性，本文采用基于二阶泰勒展开式的可靠性评价技术[15]。目标和约束性能的均值为

(15)

目标和约束性能的标准差为

(16)

式中：N为设计变量数；σxi，σxj为第i和j个设计变量标准差。

运用Isight软件集成Matlab软件对DVA振动放大系数最大值和减振效果进行6sigma稳健性分析，评估该设计方案的稳健性和可靠性。在分析前Isight做以下设置：①分析类型选择基于可靠性评价技术中的二阶可靠性方法；②设计变量概率分布设为正态分布,均值根据确定性优化结果设置，变异系数设为0.01；③振动放大系数最大值上限设为7，减振效果下限设为0.85。由分析结果图4可知振动放大系数最大值Hmax质量水平为1.001sigma，可靠性为68%；减振效果P的质量水平为8sigma，可靠性为100%，从分析结果图4来看，该设计方案有32%的可能性违反约束边界，有必要进行基于6sigma多目标稳健性优化设计，提高设计方案的稳健性。

图4 6sigma稳健性分析结果Fig.4 6sigma robustness analysis results

3.4 基于6sigma多目标稳健性优化设计

6sigma稳健优化设计的目标是设计目标的均值达到指定值和标准差最小化，降低了系统对输入参数的灵敏度，提高了系统的稳健性和可靠性。为了提高DVA的稳健性和可靠性，在考虑DVA的不确定性参数(DVA固有频率、阻尼比、质量)的情况下，对DVA的振动放大系数最大值和减振效果进行基于6sigma多目标稳健性优化设计。

在进行基于6sigma多目标稳健性优化设计前，Isight做以下设置：④优化算法选择多目标粒子群算法，多目标粒子群算法设置如表1所示；⑤在上述质量分析设置①②③的基础上，将振动放大系数最大值和减振效果质量水平下限设为6sigma。由图5和表3可知，振动放大系数最大值Hmax和减振效果P的sigma水平分别达到了8，7.956，sigma水平均大于6，可靠度都达到了100%，有较好的稳健性。至此，DVA参数设计已经完成。

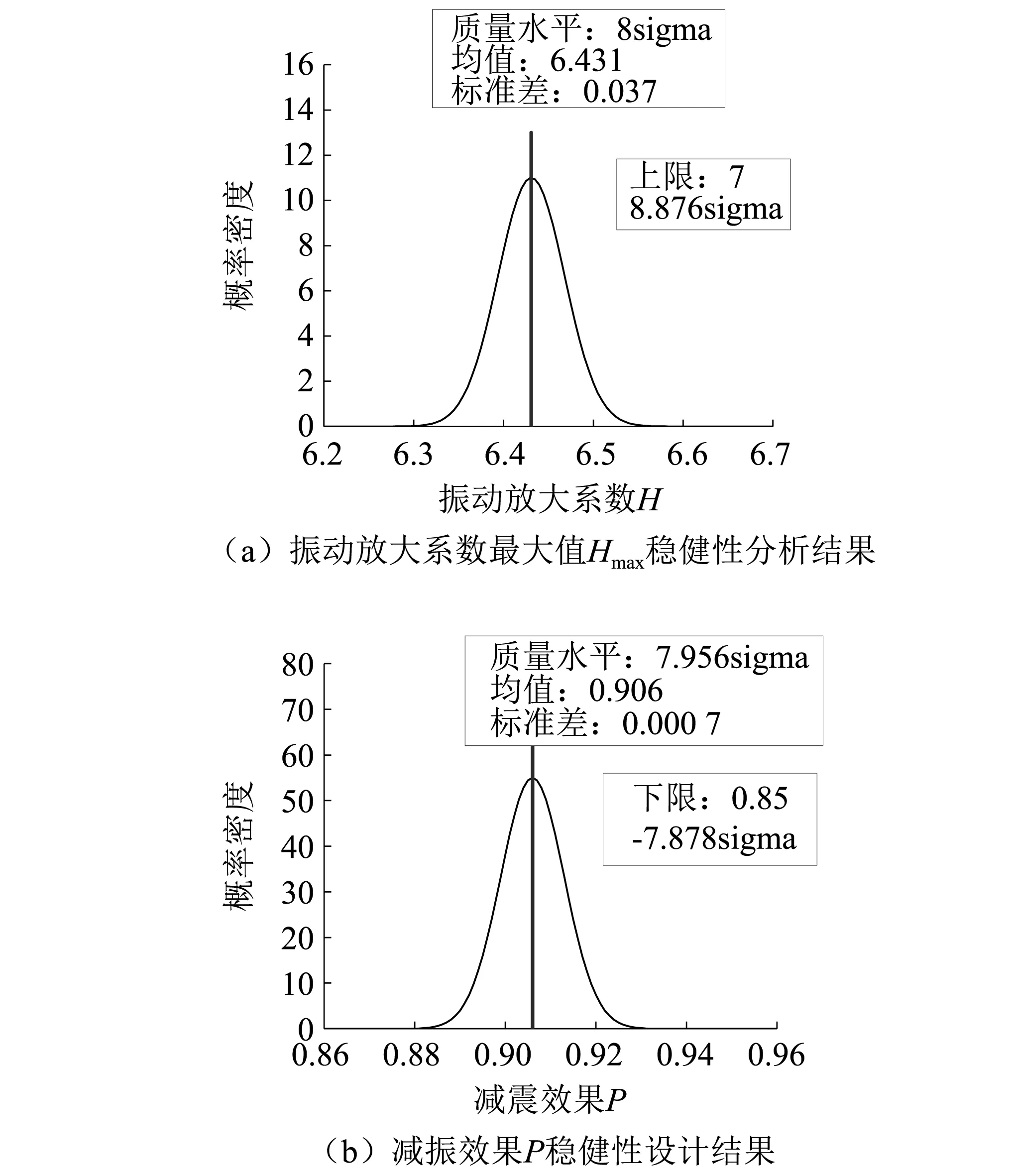
图5 6sigma稳健优化设计结果Fig.5 6sigma robust optimization design result

表3 6sigma稳健优化设计结果Tab.3 6sigma robust optimization design results

4 DVA固有频率预测、实测与装车试验

4.1 DVA固有频率预测

DVA的结构如图6所示，橡胶主簧在DVA系统中起到了刚度和阻尼的作用。在制作DVA样件前，为减少制作成本和制作时间，对DVA固有频率进行有限元仿真预测。在得到DVA设计参数固有频率fn2后，由

(17)

图6 DVA结构Fig.6 Dynamic vibration absorber structure

橡胶是典型的超弹性材料,用超弹性本构模型来描述其力学特性，Abaqus有限元建模时，采用Mooney-Rivilin超弹性本构模型，用最小二乘法拟合橡胶材料的力学试验数据得到其模型常数[16]。本文采取的Mooney-Rivilin本构模型材料参数如表4所示，金属(安装底座、质量块)力学性能参数如表5所示。

表4 Mooney-Rivilin模型材料常数Tab.4 Mooney-Rivilin material constant

表5 金属材料的力学性能参数Tab.5 Mechanical properties of metallic materials

在三维软件建立DVA数模后，导入到Hypermesh软件中进行网格划分，其中底座、质量块划分四面体网格，橡胶主簧划分六面体网格。将DVA网格模型导入到Abaqus软件中进行DVA三件套装配，建立DVA有限元模型，如图7所示。施加载荷时，约束底座的六个自由度使其固定，质量块施加位移，提取质量块的力-位移曲线求出橡胶主簧静刚度。有限元仿真时橡胶材料为天然橡胶，其硬度为50 HA，仿真静刚度为5 336 N/mm，与目标静刚度的差值为3%，满足设计要求。

图7 DVA有限元模型Fig.7 Dynamic vibration absorber finite element model

4.2 DVA固有频率实测

按照4.1节预测结果，采用硬度为50 HA的天然橡胶制作DVA，并对其固有频率进行实测。目前一般采取力锤锤击和恒定振幅激振的方式测试DVA的固有频率。对于橡胶阻尼式DVA，其固有频率的大小与动刚度有关，而橡胶动刚度的与激振振幅有关[17-20]，因此在测试橡胶阻尼式DVA固有频率时，要考虑激振振幅对DVA固有频率测试结果的影响。

本文采用力锤锤击和恒定振幅激振的方式测试DVA固有频率，如图8所示。力锤锤击力的大小与进行转向盘模态分析时相同,即锤击力在30 N。测试时，监控BBM数据采集系统中的锤击力值图，使锤击力控制在30 N，如图9所示；不共振时，转向盘Y向振动量在0.07g，故采用0.07g的恒加速度对DVA进行激振，测试其固有频率。力锤锤击力30 N时，固有频率测试结果为21.5 Hz；激振加速度0.07g时，固有频率测试结果为23.5 Hz，如图10所示，测试结果与目标值20.68 Hz的相对误差均在12%内，验证了在仅有橡胶超弹性材料参数的基础上，通过橡胶动静刚度比算出目标静刚度，仿真计算静刚度，从而预测固有频率的方法是可行的。另外，两种方式测试的固有频率结果不一样，这是由于两种方法的激振能量不一样。因此，在测试橡胶产品的固有频率时，必须明确固有频率测试加载条件。

图8 DVA固有频率测试Fig.8 Dynamic vibration absorber natural frequency test

图9 锤击力值Fig.9 Hammer force value

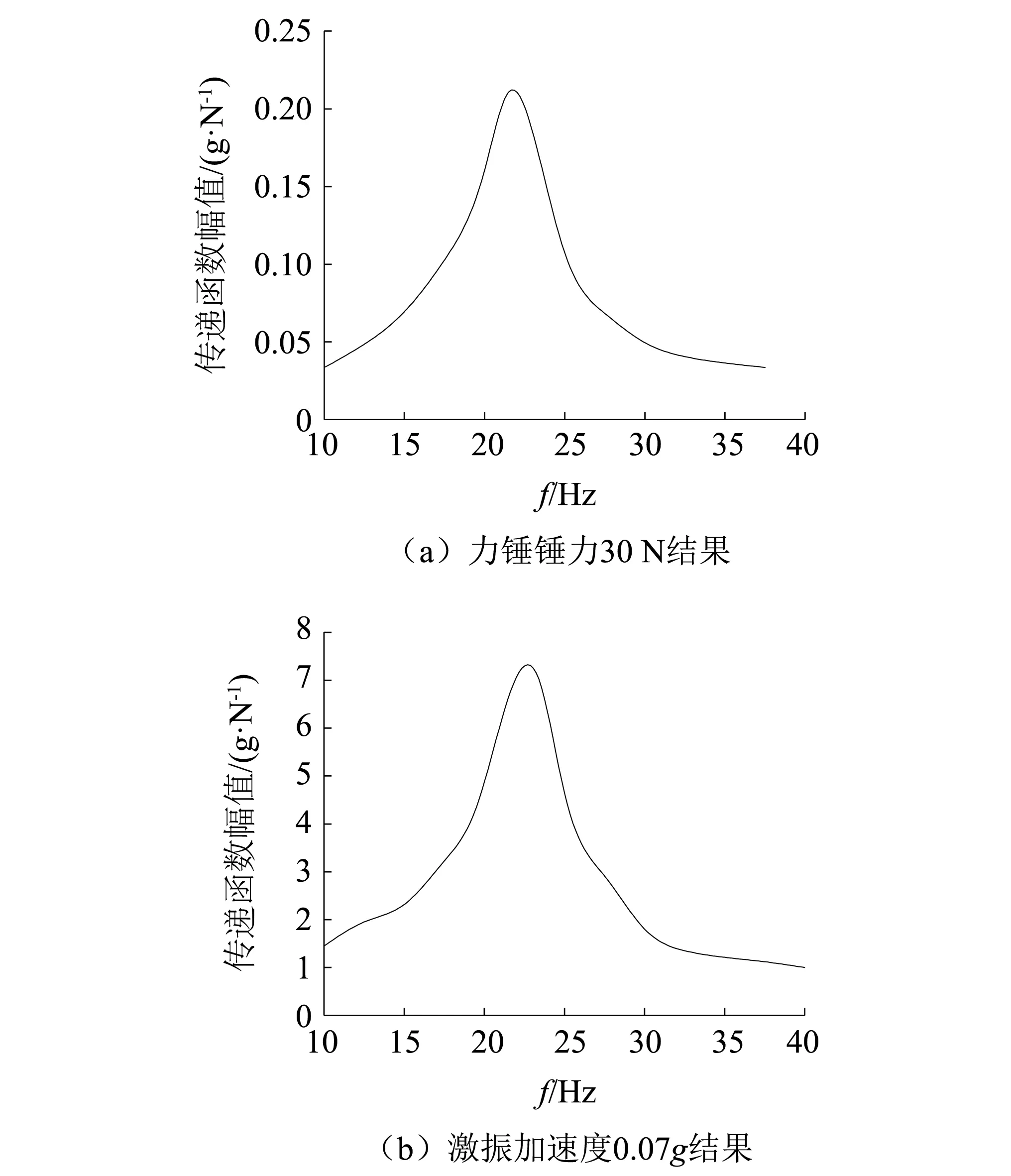
图10 固有频率测试结果Fig.10 Natural frequency test result

4.3 装车试验

制作三个DVA样件,并进行装车试验。DVA样件设计方案如表6所示。DVA安装位置如图11所示，测出转向盘Y向振动情况，DVA装车试验结果如图12所示。根据装车试验结果图12可得出以下结论:

图11 DVA安装位置Fig.11 Dynamic vibration absorber installation position

图12 DVA装车测试结果Fig.12 Dynamic vibration absorber loading test results

表6 DVA设计方案Tab.6 Dynamic vibration absorber design program

(1)对比2#和1#样件装车试验结果可知，在有制造误差的情况下，2#DVA吸振效果更好，验证了6sigma稳健设计降低了设计目标对设计变量的灵敏度，具有更好的可靠性。

(2)对比2#和3#样件装车试验结果可知，力锤锤击力30 N并不是此DVA固频测试的最佳锤击力。虽然采用30 N的锤击力测试DVA固有频率与进行转向盘模态分析时的锤击力大小相等，但转向盘系统不含橡胶，模态分析结果对锤击力的大小不敏感。锤击力的大小对方向盘模态分析结果影响不大，但对橡胶阻尼式DVA固有频率测试结果影响较大，固有频率测试最佳的锤击力有待进行更多的试验验证。