考虑时变温度作用的新型波形钢腹板组合箱梁动力特性分析

2021-02-26刘世忠丁万鹏牛思胜

振动与冲击 2021年4期

王力，刘世忠，丁万鹏，路韡,，牛思胜，冯伦

(1. 兰州交通大学土木工程学院，兰州 730070； 2. 西北民族大学土木工程学院，兰州 730030;3. 甘肃省交通运输厅，兰州 730030)

随着桥梁动态健康监测系统的不断创新与发展，基于动力特性的结构损伤识别方法被广泛应用于桥梁健康监测中。然而，模态频率作为动态健康监测方法的重要判定指标，极易受到环境温度、车辆荷载、环境振动等多因素的影响。大量研究表明[1-4]，温度作用对桥梁振动模态频率的影响不容忽视，其对结构动力特性的改变甚至超过桥梁损伤对结构动力特性的影响。

Peeters等[5]对瑞士伯恩州一座14 m+30 m+14 m的混凝土箱梁桥经过一年的动态监测，发现环境变化使结构前4阶振型频率的年相对变化比为14%～18%，且时变温度是影响模态参数的主要原因。Farrar等[6-7]分析了环境因素对阿拉莫萨峡谷桥振动频率的影响，得到一天内该桥基频的变化可达5%。周毅等[8]对东海大桥进行动态健康监测数据分析表明，温度是引起结构频率变化的主要因素之一，其与主桥各阶频率的变化呈负相关关系。杨殊珍等[9]将现场实测、理论分析和有限元仿真相结合，探讨了环境温度和边界条件对混凝土梁式桥自振频率的影响，得出混凝土弹性模量、伸缩缝工作状态变化均会影响桥梁的自振频率，但对不同桥型的影响权重不同。纵观国内外已有研究，从研究方法来看，多数学者主要依托实桥测试、统计分析(如主成分分析[10]、回归分析[11]和AR模型[12]等)、有限元仿真等途径建立温度和桥梁模态之间的关系，但该类分析方法研究的对象仅针对单个桥梁结构，具有一定的局限性。从研究对象来看，既有研究以主梁为混凝土桥梁的分析居多[13-16]，而对温度敏感性更强的钢-混凝土组合梁桥的相关研究较少，对目前国内大量兴建的波形钢腹板组合箱梁结构的研究还鲜有报道。为更深入探究温度对桥梁模态特性的影响机理，还需从梁结构振动理论出发，建立考虑温度作用的梁模态特征方程，揭示温度对桥梁模态的内在影响规律。

我国西北干寒地区干燥少云、太阳辐射强、日温差大，温度效应问题对该地区桥梁动力特性的影响不容小觑[17]。为了揭示该地区环境温度对新型波形钢腹板组合箱梁(混凝土顶板-波形钢腹板-钢底板)结构振动特性的影响机理，本文基于箱梁振动理论，提出了一种时变温度作用下考虑接触面滑移效应的新型波形钢腹板组合箱梁自振频率解析计算方法，并通过有限元模拟和模型试验梁实测对所提方法进行验证。本文理论成果旨在为波形钢腹板组合箱梁时变温度效应的研究提供必要依据和参考。

1 计算理论

1.1 等效偏心轴力计算

采用有限元方法推导任意温度分布形式作用下温度应力的计算方法。选取梁上一个单元展开分析，当纵向纤维之间不受约束而自由伸缩时，沿梁高的自由应变与温度保持一致，自由应变便可表达为

εT(y)=αt(y)T(y)

(1)

式中：αt(y)为高度y处的材料线膨胀系数；T(y)为高度y处的温度值。

由于梁上纵向纤维之间的相互约束作用，梁截面变形应服从平截面假定。则实际应变可以表达为

ε(y)=ε0+φy

(2)

式中：ε0为梁截面形心处的应变；φ为截面变形曲率。

梁温度自应变由纤维之间约束产生，为实际应变与自由应变之差，可表示为

εs(y)=ε(y)-εT(y)

(3)

纵向纤维约束自应力可表示为

σs(y)=E(y)εs(y)=
E(y)[αt(y)T(y)-(ε0+φy)]

(4)

式中，E(y)为高度y处纤维的弹性模量。

简支梁截面上自应力为自平衡应力，故内力总和应为0，即

(5)

(6)

式中：b(y)为高度y处的梁宽度；y0为换算截面中性轴。

联立式(4)～式(6)，求得ε0和φ值，即可得到梁端等效轴力P和等效弯矩MP。

P=E(y)A(y)(ε0+φy)

(7)

MP=E(y)I(y)φ

(8)

通过等效轴力和等效弯矩，求得偏心距e=Me/Pe。

1.2 温度作用下简支组合箱梁自振频率计算

聂建国等[18]提出了组合梁静力计算的折减刚度法，组合梁滑移后的刚度可以表示为

(9)

式中：E为组合梁等效弹性模量；ID为组合梁折减后的截面惯性矩；ξ为刚度折减系数；IF为组合梁换算截面惯性矩。

假设简支组合箱梁跨径为L，单位长度上的质量为m。基于应力等效原则将非线性温度场产生的温度应力等效为梁体梁端的等效温度偏心荷载，如图1所示，偏心力P0作用于梁端，偏心距为e。

图1 新型波形钢腹板组合箱梁受偏心力示意图Fig.1 Schematic diagram of eccentric force of new-pattern CSW composite box girder

CSW组合箱梁在振动时梁端轴向力P为一个变量，可以表示为

P=P0+ΔP

(10)

MP=Pe=(P0+ΔP)e

(11)

式中： ΔP为P随组合梁振动位移变化的改变量；MP为温度偏心力作用下的弯矩。故组合梁的振动微分方程为

(12)

式中：x为沿组合梁梁长的纵向距离；y为组合梁振动位移；t为时间；MP=Pe为温度偏心力对梁产生的弯矩。

将式(10)、式(11)代入式(12)可得

(13)

(14)

ΔP随组合梁振动位移y变化，二者之间关系较为复杂。鉴于振动位移y极小，故可近似用梁跨中的位移ω代替振动位移。在此假定ΔP与ω成正比关系，系数取为k，即y=kΔP。在组合梁跨中作用一个集中力F，则其在支座处的水平位移为

(15)

(16)

支点位置作用单位力引起的支点水平位移为

(17)

ΔP与支点水平位移为线性关系，则由集中力F引起的支反力变化值为

(18)

简支梁在集中力F作用下引起的跨中竖向挠度为

(19)

将式(18)代入式(19)得

(20)

根据位移互等定理知ΔP在梁跨中引起的竖向位移为

(21)

(22)

(23)

将式(23)代入式(14)可得

(24)

求解式(24)可得简支梁自振频率解析解，即

在股市中做投资，无需清楚每只股票的走势表现，只要能看清小部分个股的走势就足够了。选出自己能看清的目标盯着这些品种，从中寻找机会就足够了。

(25)

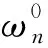
(26)

2 组合箱梁模型试验

鉴于实桥易受到结构损伤、车辆干扰和噪声等随机变量的耦合干扰，造成模态参数识别困难，使日照温度对模态参数的影响研究难以实施。本文对一座40 m新型波形钢腹板简支组合箱梁按1∶5等比例缩尺，设计、制作了新型波形钢腹板组合箱梁试验模型，暴露于西北干寒气候环境中，进行环境因素与模态参数的长期观测，分析时变温度对该类新型结构模态参数的内在影响规律及作用机理。

2.1 模型概况

试验梁采用单箱单室新型波形钢腹板组合箱梁形式计算跨径为8.0 m。组合箱梁梁高415 mm，桥面宽1 250 mm，底板宽600 mm。顶板采用C50混凝土浇筑，试验室测得混凝土翼板28 d抗压强度平均值为51.3 MPa。波形钢腹板厚3 mm，底板及底板加劲肋厚5 mm，均采用Q235钢材制作。试验梁基本尺寸如图2所示。

图2 新型CSW组合箱梁几何参数(mm)Fig.2 Geometric parameters of new-pattern CSW composite box girder (mm)

2.2 动力测试设备与方案

将该组合箱梁放置于试验大厅外，受到日光照射和风雨雪直接作用，除自质量外不受任何附加荷载，最大限度排除环境因素外的不利干扰影响。采用DHDAS桥梁环境激励实验模态测试分析系统进行自振频率的量测，该系统主要由主机、数据采集仪、数据接收节点等组成。

参考JTG TJ21-01—2015《公路桥梁荷载试验规程》，在组合箱梁顶板上表面布置拾振器，布置方案如图3(a)所示，模态及温度采集设备如图3(b)、图3(c)所示。本试验采用瞬态激振法测量其动力特性。为了使目标模态皆激发出来，需合理选择锤击位置。锤击位置根据结构振型确定，为避免所关心振型的丢失，应结合有限元模拟计算结果，避免敲击点设置在结构模态振型的结点上。测试系统采样频率为512 Hz，每次采样时长15 min。主要采用随机子空间方法[19-21](stochastic subspace identification,SSI) 进行试验数据的分析处理。动态设备采集频率的同时，运用测温仪实时采集箱梁特征截面温度和环境温度并记录。

图3 试验现场图Fig.3 Testing field

2.3 新型波形钢腹板组合箱梁温度梯度

运用本文理论计算新型波形钢腹板组合箱梁振动频率，首先须掌握该结构竖向温度分布规律。国内在钢-混凝土组合箱梁温度设计中主要参照GB 50917—2013《钢-混凝土组合桥梁设计规范》[22]，而现行各类规范中均未给出针对波形钢腹板组合箱梁温度梯度分布模式。鉴于该类新型桥梁的特点和桥梁地域差异性，在实际应用中不宜简单套用规范梯度。因此，本文对试验梁进行为期一年(2018年12月—2019年11月)的温度测试，通过实测数据建立新型波形钢腹板组合箱梁竖向温度分布函数。

试验梁场地温度时程如图4所示。由图可知，年温度时程总体呈弦曲线变化。全年最高温(35 ℃)出现在2019年7月26日，最低温(-10 ℃)出现在2018年12月9日。最大日温差(20 ℃)出现在2019年4月15日。月平均最高气温(28.5 ℃)出现于2019年7月，月平均最低气温(-7.3 ℃)出现于2018年12月。

图4 试验场地温度时程Fig.4 Temperature time-history of test site

根据如图5所示的方案进行温度采集，由于箱梁尺寸较小，温度沿其横向的分布较为均匀，因此，忽略箱梁横向温度梯度。此外，实测结果显示负温度梯度变化较小，不作为温度荷载的控制工况，本文主要研究正温度梯度工况。为简化后续计算和有限元模拟，本文选取全年中最具代表性的4 d的现场实测数据如图6所示，基于最小二乘法通过MATLAB软件拟合新型波形钢腹板组合箱梁竖向温度梯度函数。

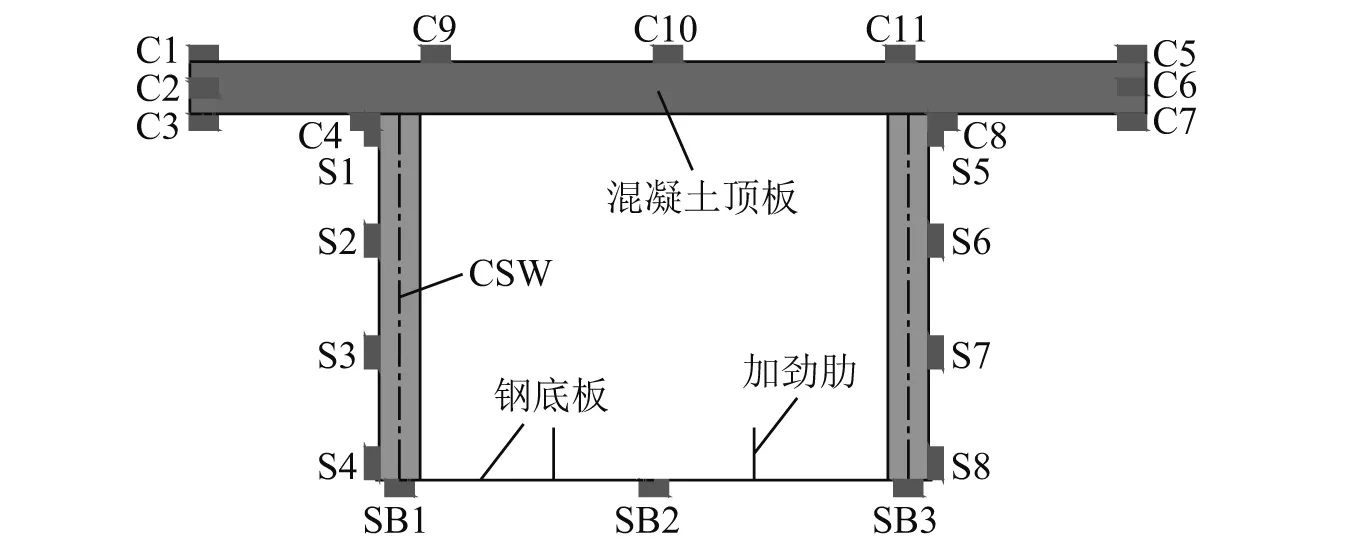
图5 试验梁温度测点布置图Fig.5 Layout of temperature measuring points of test girder

图6 测点温度时程曲线Fig.6 Temperature time-history curve of test points

由图6可知，箱梁各测点温度随环境温度也呈弦曲线变化。由于混凝土的热惰性，混凝土顶板和钢腹板最高温时间为下午3：00，混凝土底板最高温时间为下午4：00，顶底板温度存在时变相位差。另外，因钢腹板与混凝土之间热敏感性的显著差异及太阳入射角度等因素的影响，致使同一时刻在钢-混凝土结合处，钢-混凝土存在一定的温差。

本文采用测试顶面温度达最大值时刻(下午3：00)的结构温度分布形式作为最不利温度梯度，以混凝土底缘平均温度(T0)为基准，对实测数据进行处理，然后基于最小二乘法通过MATLAB软件对实测温度进行拟合，得到了组合箱梁竖向拟合温度梯度。拟合时顶板温度梯度按线性函数拟合(Tc(y)=-0.009 1y+(T0+0.546),0≤y≤65)，钢腹板温度梯度以指数函数拟合(Ts(y)=1.639 9e-0.002x+T0,65

图7 竖向温度梯度Fig.7 Vertical temperature gradient

3 有限元模型建立

3.1 有限元建模

运用ABAQUS有限元软件建立新型CSW试验梁三维有限元模型。顶板混凝土采用C3D8三维实体单元模拟，波形钢腹板、底板、底板加劲肋及横隔板均采用S4R板壳单元模拟。钢与混凝土之间嵌入无厚度黏结滑动界面单元。模型共有41 712个单元，51 516个节点。有限元模型如图8所示，模型材料参数如表1所示。

图8 试验梁有限元模型Fig.8 FEM of test girder

表1 20 ℃时材料特性Tab.1 Material properties at 20 ℃

3.2 参数取值

根据文献[23]和本文第1章理论可知，温度主要通过改变桥梁的材料弹性模量、几何尺寸、边界条件和结构内力等因素使结构自振频率发生变化。相对于材料弹性模量的温度变异性，几何尺寸、边界条件、温度应力对模态频率的影响通常可以忽略[24]。

文献[25]研究了混凝土弹性模量与温度之间的关系，并被多项研究所证实。本文也选用Xia等研究的方法对混凝土弹性模量进行计算，表达式为

E(x,y,z)=E20{1-θE[T(x,y,z)-20]}

(27)

式中：E20为温度为20 ℃时混凝土的弹性模量；T(x,y,z)为笛卡尔坐标处的温度；θE为混凝土弹性模量的温度变异系数，根据既有试验研究，当t<100 ℃时，θE取4.5×10-3℃。

贾单锋等[26]通过试验研究发现，在自然环境温度下，桥梁用钢的弹性模量随温度变化与常温弹性模量相比波动幅度较小。李国强等[27]根据试验结果拟合了钢材弹性模量随温度变化的计算公式

ET/E=-3×10-9T3+7×10-7T2-1×10-4T+1

(28)

式中：ET为温度为T时Q345钢的弹性模量；E为20 ℃下Q345钢的弹性模量。

利用式(27)和式(28)计算-20～45 ℃钢材和混凝土弹性模量的变异性，如图9所示。

图9 钢材和混凝土弹性模量变异系数Fig.9 CV in elastic modulus of steel and concrete

在有限元分析前，首先通过测得顶板上缘为20 ℃时的结构频率，并与有限元计算结果进行对比，以验证有限元模型的正确性。然后结合图9和表1，在有限元模型中对相关材料参数进行修正，并采用Lanczos法提取时变温度作用下的组合箱梁前3阶振型频率。

4 结果对比分析

4.1 时变温度与实测频率关系

甘肃省兰州地区属典型的温带半干旱气候，年极端气温为-23.1 ℃，年极端高温为39.8 ℃，最大日照温差超过20 ℃，年温差超过50 ℃[28]。该地区桥梁温度效应突出，在温度荷载作用下，桥梁结构模态参数的改变不容忽视。

本文以新型CSW简支箱梁为研究对象，将模型试验梁置于试验室外，使其除自质量外不受任何荷载作用。将试验梁进行为期一年的温度和动力特性监测。基于测得的外界环境参数与模态参数，分析环境因素对新型CSW简支箱梁自振频率的影响程度，揭示自振频率随温度的变化规律。限于试验条件，无法对试验梁进行持续观测，图10和表2列出了最具代表性的370组观测数据，通过趋势分析揭示温度变化对新型波形钢腹板组合箱梁振动特性的影响程度。

图10 实测频率与温度变化关系Fig.10 Relationship between measured frequency and temperature

表2 振型频率变化统计分析Tab.2 Statistical analysis of modal frequency variation

图10和表2为实测频率与顶板竖向平均温度拟合关系，可以看出：实测各阶频率与温度基本呈线性负相关关系，R2均大于0.86。前3阶振型频率随时变温度的相对变化范围为5.26%～7.34%。实测振型频率随阶数的增加，R2也渐趋增大，各阶振型频率的相对变化随振型阶数的逐渐增加而减小。温度每升高 1 ℃，前3阶振型频率分别降低 0.106%，0.104%，0.076%。表明越高阶振型频率变化可由温度变化的解释程度越高。因此，在结构健康监测中采用高阶振型对结构进行安全评估更具可靠性。

4.2 公式、试验及有限元分析对比

基于本文建立的新型波形钢腹板组合箱梁时变温度自振频率计算方法，运用MATLAB语言编制计算程序，计算时变温度对结构振型频率的影响。为了验证本文解析计算的可靠性，将试验梁实测拟合值(后简称：实测值)和有限元模型计算值(分为：仅考虑混凝土弹性模量变异性工况和同时考虑钢、混凝土弹性模量变异性工况)与理论解析值进行对比分析，如图11所示。

图11 理论公式值、实测值及有限元值对比Fig.11 Comparison of analytical, measured and finite element values

从图11各阶频率对比结果可知：①新型波形钢腹板试验梁振型解析解与实测值、有限元值最大相对误差为1.25%和0.79%，三者吻合较好，从而验证了本文理论方法的正确性；②由于钢材在日照温度作用下弹性模量的变异性远小于混凝土材料，时变温度作用下，同时考虑钢材和混凝土弹性模量变异性对试验梁自振频率的计算结果较仅考虑混凝土弹性模量变异性的计算结果最大增大0.3%。据此可见，顶板混凝土弹性模量的变化是新型波形钢腹板组合试验梁时变温度动力特性改变的关键因素。