基于深度学习的少样本研究综述*
2021-02-26卢依宏蔡坚勇曾远强
卢依宏,蔡坚勇,郑 华,曾远强
(福建师范大学 光电与信息工程学院,福州 350007)
0 引 言
由于基于深度学习的神经网络在目标特征的提取上具有无可比拟的优势,因此神经网络在图像处理领域中被广泛应用[1-3]。然而实验过程中发现,当训练数据非常少时,神经网络中的每个单元不得不考虑到每个样本中物体的定位和分类特征,整个神经网络会变得过拟合。因此少样本问题一直以来是深度学习研究中的一个难点[4]。
本文针对深度学习领域中少样本学习的问题,总结并分析经典及最新的方法,最后展望其未来的研究方向。
1 少样本问题的定义
在训练一个高效、精确的神经网络时,通常需要大量带有标签的数据,而在许多情况下每个类别只有一个或几个训练样本,如视频监控、卫星图像、异常检测等。同时,在如生物医疗图像识别任务中,往往会遇到特殊病例下患病样本与正常样本数极度不平衡的情况,这时正常样本数越多越影响网络性能。因此,将这种由于样本数不足或样本质量有严重偏差从而导致神经网络的性能严重下降的情况称为少样本问题。
与普通的只训练一类数据的神经网络不同,少样本学习训练集(支持集)有许多不同的类,每类又包含许多不同的样本,因此少样本学习又称为N-way、K-shot问题,其中N表示数据集共有N个类,K表示每个类中有K个样本。因为是少样本,所以K一般在1~20之间,实验中K往往取5、10、15。
2 基于深度神经网络的少样本学习方法
2.1 数据增强
数据增强是一种常用的数据处理方法。早期主要通过对数据进行空间变换,如旋转、平移、缩放、剪裁、颜色变化等[5],来生成更大数据集。随着深度神经网络的发展,也出现了许多利用如对抗生成网络(Generative Adversarial Nets,GAN)等其他网络来扩展数据的方法。
2.1.1 空间变化
Salehinejad等人[6]提出对医学图像采用径向变化方法,将笛卡尔坐标映射到极坐标来展开图像,得到一张图像很多个不同的径向变化图,不仅保留了原始图像的信息还提高了训练数据集的多样性,从而改善了神经网络的泛化性能。对现有数据集进行简单的空间变化操作生成更大的数据集,是早期在基于深度学习的神经网络中最基本的数据操作。
2.1.2 基于幻觉模型的数据增强
由于样本数很少,当训练样本中的物体发生变形时,神经网络无法准确识别。因此,许多研究人员思考如何让神经网络学会“幻觉化” 训练样本中的物体。
在Goodfellow等人[7]提出的对抗生成网络中,生成网络和判别网络的动态“博弈过程”可以生成非常接近真实图像的虚假图像。Antoniou等人[8]提出了基于生成对抗网络的数据增强方法(Data Augmentation Generative Adversarial Networks,DAGAN),利用编码器将输入图像的向量和随机向量结合,生成虚假图像。这一将GAN网络和数据增强结合在一起的方法,在实际应用上取得了很大的进展。
对于与基类完全不同的数据,Zhang等人[9]提出了一个新的网络结构Salient网络(SalNet),通过显著性数据幻觉模型来增强数据。这是第一篇将显著性图用于少样本学习的数据增强方法的论文,显著性网络很好地将图像的前景背景分割开,也是该文的一个亮点。
上述“幻觉化”[10]数据增强方法为基类数据幻化出新的样本,生成的“幻觉”样本丰富了训练数据的多样性,从而提高了神经网络识别新类别的性能。
2.1.3 基于合成多标签样本的数据增强
将多个单类别图像的标签融合来增加样本标签多样性是常见的一种数据增强方法,但目前的融合标签方法都是针对一张图片只有一个标签的情况,而自然图像往往包含多个标签。Alfassy[11]等人提出的一种新的合成样本标签的方法,成功将图像的特征与标签分离,生成训练期间未出现过的标签。该文提出的方法将训练集标签范围扩充到已给标签的交集、并集和去集中,大大提高了网络分类图像的泛化能力。
2.1.4 不同数据增强方法的比较
本节详细介绍三种最新且效果显著的数据增强方法,给出了相应的模型结构和实验中取得的准确度。其中径向变化在实验中将MNIST数据集由原本的每类20张图像扩充成每类2 000张,DAGAN中每类有5个样本,LaSO实验中的数据集包括64类已知样本和16类未知样本。
三种基于数据增强的少样本学习方法对比如表1所示。

表1 基于数据增强的少样本方法总结
不同数据增强方法各有优势。通过空间变换来增加样本数的方法简单快速易操作,却未增加样本种类。利用幻觉模型来增加样本数和通过集合运算扩充数据标签的方法在测试样本和训练样本种类一致时,可以取得很好的结果。因此,数据增强方法主要面临样本数非常少的情况下效果并不好的问题,以及测试样本和训练样本类型完全不一样的问题。
2.2 基于度量学习的优化设计
在少样本研究中有很多利用非参数化估计(如最近邻算法、K-近邻算法、K均值聚类算法)的度量学习,对样本间距离分布进行建模,使得同类样本靠近异类样本远离。一般通过构造支持集和测试集的距离来分类,重点在距离的构造上,如要分类四张不同的动物图像,并分辨出一张新图像属于前面四张图像中的哪一个动物,这时可以比较新图像和之前四张图像的特征向量距离,距离越近代表特征越像,属于同一类的概率就越大。
2.2.1 基于固定距离的度量学习
孪生网络[12]是双路神经网络,网络有两个输入,通过学习样本的特征距离来判断两个样本是否属于同一个类,输出图像相似度的概率排名。
匹配网络[13](Match Network)和原型网络[14](Protoype network)的网络结构类似。匹配网络为支撑集构建灵活的编码器,最终分类器的输出是支持集样本和询问集样本之间预测值的加权求和。原型网络提出每个类都存在一个原型表达,该类的原型是支持集在嵌入空间中的均值。
上述三个网络在最终的距离度量上都使用了固定的度量方式,如余弦距离、欧式距离等,这种模型结构下所有的学习过程都发生在样本的嵌入阶段。
2.2.2 基于可学习距离的度量学习
一些研究人员提出,在度量学习中,度量方式也是网络中非常重要的一环,人为规定的度量方式在学习过程中会限制网络的性能。因此,文献[15]提出训练一个相关网络来学习度量距离,最终网络输出一个0~1的值,表示支持集和询问集的相似程度。同时,网络的损失也应该针对不同的任务而改变,在相关网络中解决的是回归问题,而非分类问题,所以使用均方误差(Mean Square Error,MSE)代替交叉熵(Cross Entropy)[16]。
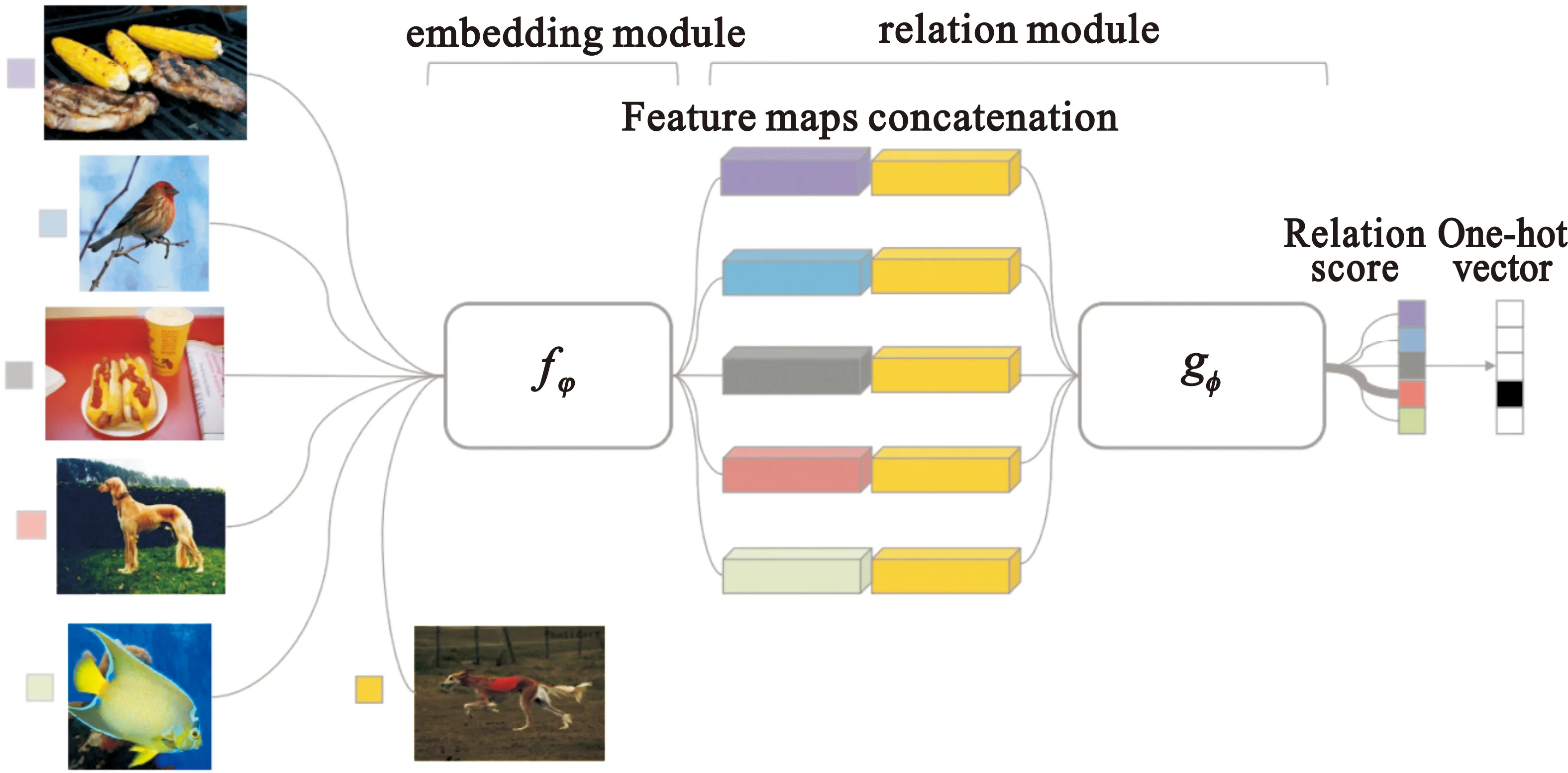
图1 相关网络结构图[15]
2.2.3 度量学习方法总结
本节介绍两种基于度量学习的少样本方法,下面对比了每种方法使用的网络模型,给出每一个网络所使用的数据集,以及在Mini-ImageNet数据集上部分网络取得的准确度。其中原型网络和匹配网络是由4个卷积块组成,相关网络由6个卷积块加2个全连接层组成。
两种基于度量学习的少样本学习方法对比如表2所示。与其他方法相比,第一种使用欧式距离或余弦距离等固定距离的度量方法在单样本学习(one-shot learning)中可以取得非常好的结果,但这种人为设计的度量方式存在一定局限性。因此,研究人员提出使用深度神经网络来学习样本之间的特征距离的方法,同时也使用了不同的损失函数来训练网络。从实验结果可知,可学习的度量方式优于固定距离的度量方式。

表2 基于度量学习的少样本方法总结
2.3 元学习
元学习是一种利用以往经验来处理新任务,让网络学会如何学习的方法。元学习的目标是让网络在每个任务中快速学习这个任务最优解,在不同任务之间学习跨任务的学习能力。文献[17]对元学习进行简单定义,指出元学习是通过选择参数来降低网络在整个数据集的损失函数。
2.3.1 基于优化方式的元学习
基于优化方式的元学习使网络不再从样本中学习而是从任务中学习,最大化网络的泛化能力[18]。Andrychowicz等人[19]提出一种让网络学习如何学习的方法,利用长短时记忆(Long Short-Term Memory)优化器实现元学习过程。同样,在Rav等人[20]提出的方法中也使用了LSTM结构。Rav等人发现,在少量数据下,使用的一般梯度算法,如momentum、adagrad、adadelta、Adam[21]等,需要经过多次迭代才能完成优化,无法应用于需要快速学习不同任务的元学习中[22-23]。因此需要一个通用的初始化参数,可以让模型从一个很好的初始参数开始训练,在面对不同的任务时模型能实现快速学习[24]。
Finn等人[25]提出与模型无关的元学习方法(Model-agnostic Meta Learning,MAML),既与模型结构无关也不增加新的参数,且可以和任何使用梯度下降训练的模型兼容。同时,MAML不仅可以用于图像分类问题,在回归和强化学习上也取得了很好的结果,因此MAML在元学习领域被广泛应用。
Nichol等人[26]提出把MAML中对参数求二次导改为求一阶导可简化计算,从而提高网络速度。同时,作者还对MAML算法中初始化参数的更新规则进行修改,提出了Reptile算法。
基于优化方式的各种元学习方法将深度学习的研究从网络结构的优化变为参数优化,未来应进一步探索如何取得更有利的参数。
2.3.2 基于参数的跨任务元学习
文献[27]提出一种与任务无关的元学习(Tast-agnostic Meta Learning,TAML)算法,通过加入正则化项提高网络的通用性。具体而言,作者提出两种新颖的TAML算法范式,一种使用基于熵的TAML度量,防止模型预测过程中偏向某一具体任务;另一种使用基于不平等最小化的TAML度量,对初始模型进行元训练,使模型在面对不同任务时的差异更小。
2.3.3 基于模型权值的元学习
Sun等人[28]提出了一种元迁移学习方法,针对目前的元学习进行改进,将迁移学习和元学习结合,得到更优的性能,证明MAML具有很强的适用性,也为下一阶段如何将元学习算法和迁移学习等其他方法结合提供了可能。
2.3.4 对比
本节归纳三种元学习方法的不同,并给出在Mini-ImageNet数据集上的准确度,其中数据集设置为1-shot 5-way。
三种基于元学习的少样本学习方法对比结果如表3所示。基于优化方式的元学习适用性很强,可以和许多神经网络模型结合使用,但是这种方法计算量大,因此要求网络结构不能太复杂,否则会出现梯度爆炸或梯度消失的情况。从实验结果可看出,Reptile算法在图像分类任务的准确度上略差于MAML算法。基于参数的跨任务元学习效果虽好,但考虑到基于熵的方法的输出取决于模型的输出函数,因此它更适合特定的分类或回归任务。

表3 基于元学习的少样本方法总结
在未来的研究中,可以思考能否将元学习与数据增强或度量学习等方法相结合。并且元学习还面临一个重要问题,即如何在保证计算量的同时提高模型复杂性。
3 少样本学习的未来研究方向
随着深度学习的应用越来越广泛,少样本学习问题也引起了重视,现有的少样本学习方法虽然已经取得了很大的进展,但仍有很大的进步空间,在此提出几点未来的研究方向:
(1)提高训练样本的复杂度
少样本学习最终目的是能广泛应用于实际生活中,然而在上述方法的实验中,目前大部分少样本学习模型训练使用的数据集为Omniglot 和 ImageNet,这两个数据集样本的种类与复杂的现实生活相比过于简单,虽在实验中可以取得不错的准确率,却无法反映模型在实际应用中的效果,在未来的研究中应着重研究困难样本的少样本学习。
(2)无监督学习
监督学习是目前深度学习中最热门的领域,但是许多情况下无标签的数据集远比有标签数据更容易获得。例如,在通过特征向量的距离来分类的度量学习中,是否可以使用无标签的数据来训练。借助大量无标签的数据来帮助少量有标签的数据进行学习,是未来研究的一个方向。
(3)神经网络的深入
少样本学习面临的最大问题之一是过拟合现象,神经网络中成千上万的神经元会因为样本数太少而过于偏向训练样本。许多元学习方法往往受限于过于简单的网络结构,因此优化神经网络内部的神经元,使其具有更强的泛化性能,将对少样本学习有更大的提升。
(4)其他领域的少样本学习
现阶段少样本学习主要解决的是分类问题,然而如何利用元学习跨任务学习的能力,将少样本学习扩展到目标检测任务和图像分割任务中也是非常重要的。
4 结 论
本文通过对比少样本学习在图像处理领域的最新研究,从不同角度总结并分析了当前少样本学习的最新成果。三种典型的数据增强方法能成功扩充样本数据量,虽行之有效,却未从根本上解决少样本问题。度量学习的少样本学习,当样本数过于少时,度量学习往往会发生过拟合现象,具有一定局限性。经典的元学习方法,优点在于可以快速处理训练集中从未出现过的新样本,但是元学习复杂的训练过程和过于简单的网络结构使其无法达到更高的精度。
