基于机器学习的用户升级预判研究

高 和，籍汉超，陈 玲（.中国联通研究院，北京 00048；.亿览在线网络技术(北京)有限公司，北京000）

0 前言

随着数据“爆炸式”增长的信息时代的到来，运用人工智能技术从海量数据中获取价值信息，进而推动业务发展、支撑运营决策，已成为企业发展的关键。例如，今日头条既没有传统媒体的内容优势，也没有门户网站的海量用户资源，却凭借数据挖掘和个性化推荐技术迅速崛起，成为移动端资讯市场中的一匹“黑马”；网易云音乐虽然在音乐版权方面不具优势，并受到阿里与腾讯两大巨头的夹击，但凭借精准多样的推荐和基于大数据的优质运营，在中国数字音乐市场占有着一席之地。

对于通信运营商而言，覆盖全国的移动网络承载着上亿级用户，人工智能中的机器学习工具可帮助运营商分析用户特征、建立用户画像。目前，运营商在用户性别及年龄判断、用户离网预测、用户网络满意度分析等方面已经形成了一些研究成果，这些成果对企业了解用户，制定用户维系挽留策略，制定感知提升策略提供了依据，体现了机器学习的应用价值。

当然，这些研究成果远远不够，还有更多的领域需要人工智能的协助支撑，例如，在用户变更业务套餐的意向方面，目前还鲜有研究。如果能事先洞察用户的套餐变更需求，甄选出其中需要升级套餐内容和价格的用户，就能够提升营销推荐的精准度，增强关怀服务的主动性，提高用户向高ARPU 套餐的转化率。鉴于此，本文在综合应用逻辑回归、因式分解机、深度神经网络3种机器学习算法的基础上，提出用户是否会向高ARPU 套餐升级的预判模型，并使用移动网络业务域的真实用户数据验证了模型的有效性与准确性。

1 机器学习算法

在预测移动用户变更套餐的意向时，本文将其转化为一个二分类问题，即套餐升级与否，常用的分类模型有：以逻辑回归算法为代表的线性模型、以梯度提升树为代表的树模型、以朴素贝叶斯为代表的贝叶斯模型、以神经网络为代表的深度学习模型等。不同模型适合于不同的场景：线性模型相对简单，计算量小，更适合输入特征多、样本数据量大的场景，但如果特征线性可分性差，则容易欠拟合；树模型的优势在于可解释性强，非线性拟合效果好，但对于缺失数据十分敏感，不适用于特征量超大的场景；贝叶斯模型在小规模数据上表现较好，如果数据规模很大，一般建议使用其他模型；近年来，随着云计算的发展，计算能力得到了前所未有的增强，计算量很大但表现能力很强的深度学习模型得到了越来越多的应用。

工信部统计的移动电话普及率已经超过了100%，运营商拥有上亿级的移动用户信息和海量的用户行为数据。这部分数据分为2 类，一类是连续特征数据，另一类是离散特征数据。连续特征可以经过简单的处理直接输入到机器学习模型，但离散特征——比如用户职业特征（教师、工人、职员等），则需要独热（One-hot）编码数字化处理后才能输入。One-hot 编码，即使用N位状态寄存器来对N个状态进行编码，比如使用［1，0，0，...］代表教师、［0，1，0，...］代表工人等等。经过独热处理后，一维特征会转化为多维特征，而维度的个数跟离散特征的取值个数有关，其中大部分取值为零，因此会产生严重的特征稀疏问题。

因此，本文选取了较为经典的、适用于大规模数据和稀疏特征的3 种分类算法（逻辑回归、因式分解机、深度学习神经网络）进行研究对比。

1.1 逻辑回归

逻辑回归（LR——Logic Regression）是传统机器学习中的一种分类模型。逻辑回归以样本特征的线性组合作为自变量，使用sigmoid 函数将自变量映射到（0，1）上，其预测函数为：

模型假设预测函数的值即为结果为1的概率。

逻辑回归算法参数个数较少，具有计算量小、计算速度快、占用存储资源少、易于并行等特点，在处理超多维度特征问题上有独到的优势，在生产环境中有非常广泛的应用空间。但模型本身一方面对特征与预测结果的线性相关性依赖性很高，另一方面无法表达特征直接的组合关系，因此对人工特征处理提出比较高的要求。

1.2 因式分解机

因式分解机（FM——Factorization Machine）是对逻辑回归模型的扩展。因式分解机基于逻辑回归，加入了特征两两交叉的交叉项，其自变量扩展为：

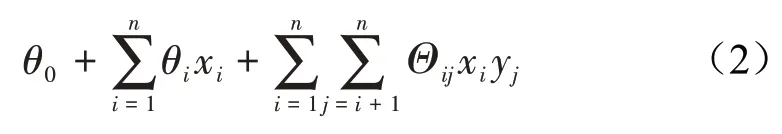
为适应高维稀疏特征，基于矩阵分解原理提出隐藏矩阵v代替参数矩阵Θ，令

其中m为隐藏矩阵深度，可以根据实际情况进行调整。

在一般的线性模型中，各个特征是独立考虑的，没有考虑特征与特征之间的相互关系。但实际上，大量的特征之间是有关联的。以用户年龄与终端类型为例，一般年轻人关注手机的运行内存，并乐意购买新上市的机型，而老人可能更偏爱蓄电时间长、功能简易的机型。很明显，用户年龄特征与终端类型特征之间有一定关联关系。与线性模型相比，因式分解机能够找出有关联的特征组合，显然是很有意义的。

1.3 神经网络模型

逻辑回归等浅层学习模型虽然简单有效，但是一个重要特点是依靠人工经验预先提取出样本数据的特征，特征提取的好坏就成为影响整个模型系统性能的重要因素，为此，通常需要开发人员耗费精力、深入理解待解决的问题，才能提取出合适的特征以便浅层模型处理。

深度学习，其实质就是包含很多隐层结构的机器学习模型。层次化的结构使其可以通过学习和组合低层特征，形成更为深层意义、更加抽象的高层特征，最后得到数据的分布式特征表示的一种特殊网络模型。和人工特征提取方法相比，深度学习通过大量数据训练提取特征对数据中的丰富内在信息更有代表性，从而提高了分类和预测的精度。

深度学习最基础的模型为神经网络（NN——Neu⁃ral Network）。神经网络可看作一系列逻辑回归的网状组合，图1展示了一个三层神经网络的结构，图中节点的计算方式为：

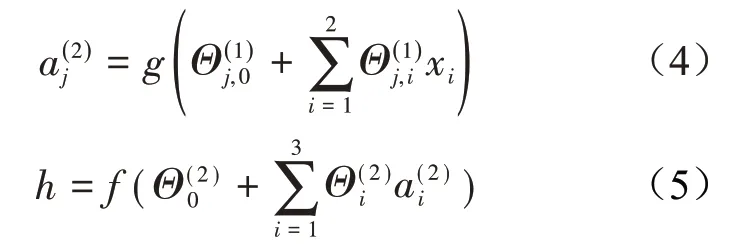
其中g(*)与f(*)为激活函数，可能为sigmoid 函数，也可能根据实际需要调整为其他形式。

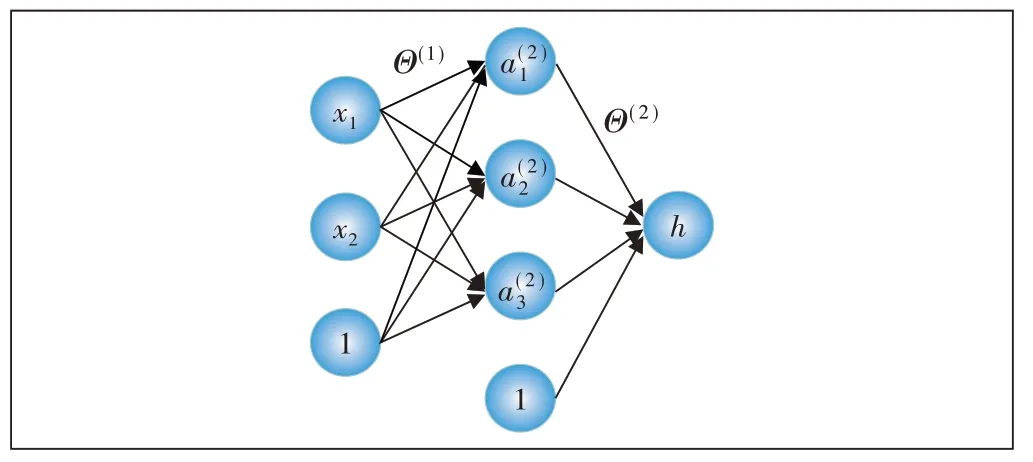
图1 神经网络结构图

从网络连接关系可以看出，如果选取的激活函数是非线性函数，只要网络结构足够复杂，神经网络可以表示任意的非线性和特征组合关系。

2 用户升级预判模型

2.1 系统建立

本文数据集来自移动网络业务域的用户数据。采用用户画像特征（省份、性别、年龄、职业、手机等）、2018 年某月的用户运营信息（套餐、VIP 级别、付费类型等）、和该月份用户消费情况（月话费、月流量值、月通话时长等），共70 个维度作为用户特征。由于没有进行实地推广实验，所以采用一年后该月份仍在网、转换了套餐、并且该月总流量大于等于30 GB 并且消费大于等于129 元（5G 最低消费套餐标准）的用户近似作为正样本，取得数据共1 000 万条。用户升级预判系统的整体处理流程如图2所示。

图2 用户升级预判系统流程

2.2 数据清洗和特征处理

首先进行数据清洗：部分用户并没有任何升级意向，如行业用户、合约一年后仍在期用户等需要剔除；还有部分用户活跃度很低，（对于预测目标）升级几率很小，比如每月话费小于40 元、月流量小于100 MB 的用户，也将其去除。最终剩余样本数140.88 万条，其中正样本2.21万条，其余为负样本。

然后根据样本特征的不同类型分别进行处理。对于离散值特征，如性别、职业等，先将其标签转化为数字，然后再使用独热编码将一维特征转化为多维。比较特殊的是，有些特征可能包含的标签种类很多，而长尾标签包含的样本又很少（如手机型号），此时需要截取头部标签再进行独热编码，其余长尾标签统一编码为未知。对于连续值特征，如年龄、月流量值等，有2 种处理方式：对于年龄等数值大小对比非线性的特征，按高低分为若干个区间，等同于离散特征，将各数值区间进行独热编码；对于数值相对线性度较高的特征，可以剔除一部分（比如头部2%）的异常值，然后使用最大值-最小值法进行归一化处理。本文采用的数据集中每条样本收集到原始特征共77个，经过独热编码处理后，每条样本的特征维度扩展为18 959维。

2.3 训练集、验证集和测试集

将样本数据按比例7∶2∶1 分为3 份，分别作为训练集、验证集和测试集，如表1所示。其中训练集用来对模型进行训练；验证集则在训练过程中对训练模型进行验证，提前终止训练，令模型保持在最优状态；测试集则对各个模型进行评估。由于正负样本数量相差悬殊（达到1∶62），直接输入模型，如果模型将所有样本都预测为负样本，则准确率就能达到98.3%，显然不是期望的目标。因此在训练过程中，一般对负样本进行随机采样，使得正负样本比例达到1∶1。测试集则不需要采样处理。

表1 数据集划分

2.4 模型参数设定

本文使用逻辑回归、因式分解机与四层神经网络来训练模型。设定：因式分解机的隐藏矩阵深度为32，神经网络隐藏层层数为2，每层节点数大小分别为256 与32，学习率（Learning Rate）为0.02，使用随机梯度下降（Stochastic Gradient Descent）优化算法，批处理大小（Batch Size）32，累积训练50轮次。各模型超参数量和可训练参数量（一定程度上代表模型复杂度）对比如表2所示。

3 模型结果分析

图3 与图4 比较了逻辑回归、因式分解机、神经网络3 个模型在训练过程中，训练数据集的准确率与验证数据集准确率变化情况。

可见，越复杂的模型（一般等同于可训练参数更多的模型），最大准确率越高。在验证集上，神经网络的准确率可达84.35%，而逻辑回归的准确率最高只有82.84%。并且越复杂的模型收敛速度也越快。神经网络可以在第1 次迭代后就达到了80%的准确率，因式分解机需要3 次迭代，逻辑回归则需要5 次。同时，越复杂的模型，在训练过程中也愈加不稳定，也更可能达到过拟合状态（即训练集准确率上升，验证集准确率不再上升或下降）。

图3 基于训练数据集的模型准确率对比

图4 基于验证数据集的模型准确率对比

由于模型最简单，逻辑回归模型基本没有出现过拟合状态，训练集准确率和验证集准确率基本一直在增长，并且相差不大。与之对比，因式分解机随迭代次数增加，训练集准确率一直在上升，但验证集准确率到20次迭代基本就保持稳定，并且最大验证集准确率跟逻辑回归相近，说明本实验中数据对于交叉特征并不敏感，所以加入交叉特征对验证集准确率提升不大，但由于模型更加复杂，所以训练集准确率能够达到更高的水平。使用神经网络后，由于不仅能匹配交叉特征（与预测结果间的关系），还能匹配非线性特征，所以验证集准确率有了进一步提升。当然由于模型进一步复杂化，过拟合现象同样难以避免。

对于训练到最优状态的模型，逻辑回归、因式分解机、神经网络的ROC 曲线如图5 所示。AUC 值分别为0.899 6、0.901 9、0.920 2，结果都比较理想，说明选取的特征能比较好地区分出正负样本，并且（对于连续特征来说）线性相关度比较高。

图5 模型ROC曲线对比

事实上，上述通用评估指标并不太适用于本文的建模目的。本文最终目的是希望建立一个模型，使得可以使用较小的推广成本，即较少的推广人数，覆盖尽可能多的目标用户，因此对于在相同推广人数情况下能更加关心覆盖到的目标用户数（正确召回人数）和覆盖的目标用户数占所有目标用户的比例（正确召回率），而并不在意对于负样本的预测情况。为有效评估模型质量，使用没有参与训练过程的测试集进行评估，目标为通过预测排序来使用更少的推广用户覆盖尽量多的目标用户。为了对比基于机器学习方法的模型与基于一般规则的模型的效果差异，采用用户月流量值（DOU）排序与月消费（ARPU）排序作为基于一般规则的模型，对比情况如图6所示。

图6 模型召回量对比

使用机器学习模型，向测试数据集中的10 000 个用户做推广时，能覆盖934～1 089 个目标用户，召回率达到50%，但同样情况下使用规则模型，只能覆盖241～348 个目标用户，召回率只有10%～15%。在给30 000 人做推广活动时，机器学习模型能覆盖1 431～1 607个目标用户，召回率65%～72%，使用规则模型只能覆盖530～1 036 个用户，召回率24%～47%。可见使用机器学习模型的效果远远优于使用规则排序的模型。

4 结论

本文提出了一种基于机器学习的用户升级预测方法，使用逻辑回归、因式分解机、深度神经网络3 种算法实现了该方法，预测准确率分别可达82.84%、83.14%、84.35%，AUC 分别达到89.96%、90.19%、92.02%，并且3 种算法的召回效果都远优于传统的ARPU/DOU 排序模型。实验对比可见，神经网络算法的预测表现最佳，但算法复杂度高，耗费时间和算力更多，逻辑回归算法的预测结果与神经网络算法的差距并不明显，因此，逻辑回归其实已经可以满足一般化的使用要求，如果对逻辑回归的预测精准度不够满意，则可以使用更复杂的因式分解机或神经网络进一步优化预测效果。该研究结果适用于挖掘潜在高价值（高ARPU）用户，为运营商制定营销服务策略和网络保障方案提供了依据。尤其在5G 商用初期，结合5G 套餐特征，本预测模型可拓展应用于推荐5G 潜力用户，从现网用户中挖掘出有需求、有能力、有兴趣使用5G套餐的用户，这对于运营商推广5G业务、争夺首批用户具有重要意义。