涡旋压缩机激励载荷反求分析
2021-02-25谷欢欢文智明王竞杰张荣婷张金圈魏会军
谷欢欢,文智明,王竞杰,张荣婷,张金圈,魏会军
(1.空调设备及系统运行节能国家重点实验室,广东 珠海517907;2.珠海格力电器股份有限公司装备动力技术研究院,广东 珠海517907)
涡旋压缩机广泛应用于商用多联机空调器系统等制冷设备,涡旋压缩机的振动是引发配管系统振动的主要原因之一。为了考察稳定运行时振动如何对系统配管的应力应变产生影响,通常首先要掌握压缩机载荷激励分析方法。
对于有限元分析软件在空调配管设计中的应用研究,合肥工业大学卢建伟[1]及其团队从2004年就开始有所涉及,并对压缩机载荷测试分析方法[2]在专利中进行了较详细说明,又采用该方法在VC++平台上开发了中央空调配管系统动力学仿真分析软件[3],载荷反求也被封装在该软件中。此后该团队还对载荷分析方法在启动运行阶段和时变工况条件下的载荷反求[4-5]进行了研究。但是载荷反求主要是以转子压缩机为研究对象进行的激励反求。
对于转子压缩机,其激励力主要是不平衡离心力和切向气体力引起的阻力矩,且从其振动响应看,这其中的气体阻力矩影响最大,最为关键。而涡旋压缩机载荷特性与转子压缩机相差甚远。本文主要对涡旋压缩机激励载荷进行反求,并通过分析确定涡旋压缩机激励反求力和力矩的大小及添加方式。
另外,本文主要针对变频涡旋压缩机[6-9]进行研究,故载荷反求包含了整个运行频率范围内的载荷,即最终给空调系统的激励载荷是随运行频率变化的载荷。
1 涡旋压缩机激励载荷分析原理
1.1 涡旋压缩机结构和载荷特性
涡旋压缩机与转子压缩机尤其是单缸转子压缩机的振动特性完全不同,如图1所示,图中X、Y、Z分别为压缩机的切向、径向、轴向。单缸转子压缩机由于其偏心转子结构,其切向气体阻力矩大,振动特性也主要以切向为主。而振动位移也是低频运行时最大,系统上只需考虑低频运行频率下的振动位移激励即可。

图1 不同运行频率下单缸转子压缩机振动位移
涡旋压缩机则完全不同,其振动位移数值远小于单缸转子压缩机,但其最高运行频率比转子压缩机高,空调系统上管路运行应力应变主要在高频运行时容易超标,故重点关注高频运行时的激励载荷特性。
涡旋压缩机的结构如图2所示。涡旋压缩机泵体由一对动静涡旋盘组成,其组成多对压缩腔,相邻腔间压差小,故气体阻力矩远小于转子压缩机,从振动位移可以看出涡旋压缩机的低频振动特性。

图2 涡旋压缩机结构示意图
不同测点振动位移特性如图3所示,随运行频率变化的振动位移如图4所示,图中X、Y、Z分别为压缩机的切向、径向、轴向。各测点具体位置在下文2.1节中详细说明。
从图3和图4以及与图1对比可以看出:
(1)涡旋压缩机振动位移远小于单缸转子压缩机的振动位移,且振动位移主要由压缩机运行频率的1倍频贡献;
(2)涡旋压缩机的振动位移主要以径向和切向振动为主,轴向振动仍是最小振动,在做激励载荷反求时忽略轴向振动;
(3)随着运转频率增大,径向振动位移呈增大趋势,而切向振动位移呈减小趋势。
综上,涡旋压缩机激励载荷特性以径向振动和切向振动为主,且在高频运行时,径向振动更为显著。

图3 涡旋压缩机60 Hz振动位移及频谱特性

图4 涡旋压缩机不同运行频率上焊点振动位移
1.2 涡旋压缩机载荷反求原理
对于3 对极的涡旋压缩机,其电机激励力主要为6 倍频及其谐波,而振动位移峰值均为1 倍频,如图3(b)所示,其他所有高频激励均不做考虑,故其激励扭矩、径向力和轴向力主要由气体激励和离心力产生,然后分别通过静盘-支架-外壳和动盘-曲轴-支架-外壳两条路径向外传递引起压缩机振动。按照图5所示的简化激励反求方法获得压缩机的载荷特性,考虑到轴向力对分析的影响较小,忽略轴向力的影响。
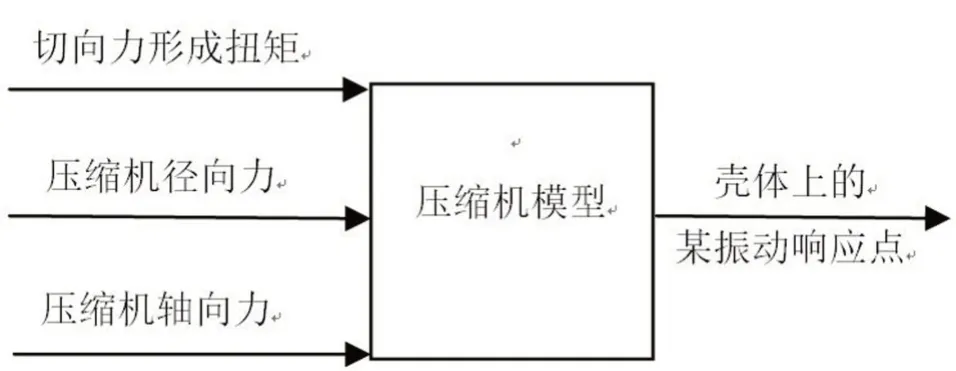
图5 压缩机载荷识别方法示意图
本文主要采用传递矩阵法对涡旋压缩机受到的激振力和力矩进行反求。传递函数中未考虑旋转方向,只考虑平动自由度。压缩机上的n个响应点的振动位移可以用下列传递矩阵表达:

其中:fx,fy,fz,Mx,My,Mz——各方向的激振力和激振力矩;ux1,uy1,uz1,uxn,uyn,uzn——压缩机表面第1个和第n个响应点各方向的振动位移;Hx1fx为激励力fx作用到ux1的传递函数,,其他类似。
对于涡旋压缩机而言,忽略轴向力影响。不平衡惯性力为一个空间变化的径向力,其运动轨迹为圆。切向气体力导致的力矩为轴向力矩。涡旋压缩机表面的各响应点的振动位移可表示为

若已知振动位移响应和传递函数,其激振力可表示为
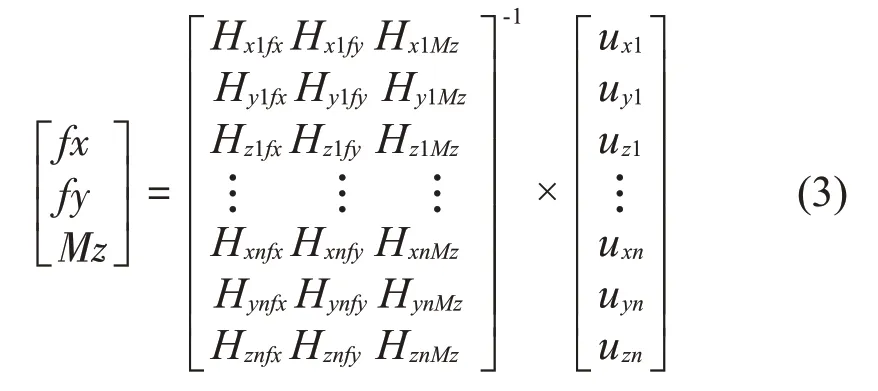
根据上述原理,若要得到反求的激励载荷,那么首先要得到振动位移响应和传递函数。本文中振动位移响应通过压缩机单机试验测试得到;传递函数中包含两部分,分别是径向力传递函数和切向气体力导致的轴向力矩传递函数,利用有限元仿真分别通过添加单位径向力和单位轴向力矩提取。
2 激励反求实现过程
2.1 涡旋压缩机振动响应测试
吸气管和排气管是涡旋压缩机与空调系统直接连接位置,但在激励反求载荷过程中,壳体上的测点是内部激励力最近反映测点。故在不确定测点位置情况下,选择测点如下:
根据涡旋压缩机激励特性和传递路径,壳体高度方向选择图2中所示的压缩腔、上焊点、电机、下焊点所在高度,并在周向上测试互相垂直角度逆时针均布4点的振动位移。0度具体位置可参考图7示意图,设吸气管顺时针方向两机脚中心45度位置为0度角。以上全部测点共计16点。
测试工况:采用空调系统名义制热工况,如表1所示,压缩机装上自身配用的减振垫。将其放置在处于半消声室地面中央的刚性平台上(不带固定螺栓),压缩机用非刚性连接管接入置于半消声室外的代用制冷系统。按照30 Hz、60 Hz、80 Hz、90 Hz~130 Hz 间隔10 Hz 测试不同运行频率下振动位移情况。

表1 压缩机测试工况
振动位移采用LMS Test.lab测试软件和PCB振动加速度传感器进行测试。最终可得到振动位移响应如下:

2.2 涡旋压缩机有限元模型
论文中关注的涡旋压缩机激振力主要是根据压缩机表面响应点的振动位移求得,且主要是低频成分,即130 Hz 以下。如图6所示。压缩机第一阶柔性模态频率为轴承转子支撑组件模态,为看清振型,隐藏压缩机壳体。其固有频率为400 Hz以上,很难被激发,在建模时,可忽略压缩机内部零部件。
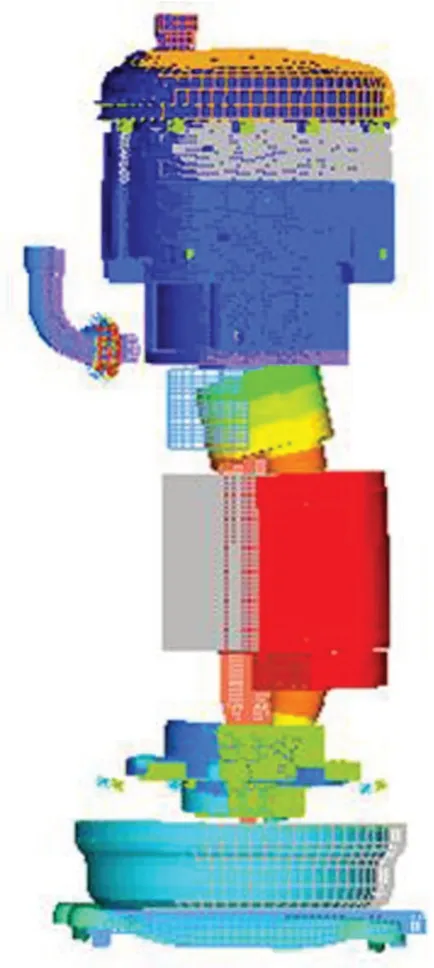
图6 涡旋压缩机第1阶柔性模态(519 Hz)
如图7所示。压缩机的有限元模型采用中空模型,内部零部件作为质量点添加在压缩机重心位置。力和力矩的位置作用在质心上,质心通过rbe3 单元分解在上下焊点所在的平面上。压缩机减振垫固定在地面上。力矩方向为沿电机轴垂直向上。径向力通过两个互相垂直作用在质心且时间相位相差90度的力实现,如图7中黄色和蓝色箭头所示。

图7 压缩机载荷识别有限元模型
2.3 涡旋压缩机力和力矩激励下频率响应分析
利用MSC 有限元分析软件中的频率响应分析模块得到传递矩阵。
如式(5)所示,先施加单位径向力得到单位径向力的振动位移响应。将单位力作用在压缩机重心位置,获取各响应点的振动位移。已知径向力的运动轨迹是圆,为了模拟该径向力,在有限元中,需要添加两个相互垂直幅值相等相位相差90 度的两个力合成。X方向作为参考相位,相位为0 度,Y方向的相位为90度。那么有:
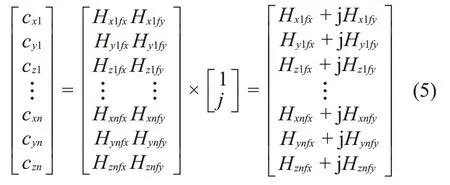
然后如式(6)所示,施加单位力矩得到单位力矩下的振动位移响应,有:

将式(5)、式(6)代入式(3),可得反求的激励载荷为
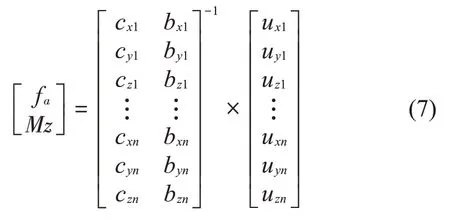
其中:fa为径向力的幅值,其也是X方向和Y方向幅值。
2.4 变频涡旋压缩机不同运行频率响应
涡旋压缩机不同运行频率下振动位移响应不同,而不同运行频率下的传递函数为同一矩阵,故将不同运行频率下振动位移代入式(7),可求得不同运行频率下的激励激振力和力矩。本文中可求得运行频率30 Hz、60 Hz、80 Hz、90 Hz~130 Hz间隔10 Hz的激振力和力矩。
空调管路系统中,压缩机激励力和激励力矩需添加所有运行频率下的激励,故采用最小二乘法拟合得到。
3 结果讨论与分析
在反求压缩机激振力时,对于传递矩阵法而言,传递函数越全越多,得到的激振力就越准确。但考虑实验测试布点的限制,不可能测试无限多测点。本文讨论在反求误差较小的情况下,响应点位置和个数选择要求。并在确定测点后采用该方法利用吸气管和排气管上的振动响应结果分别采用测试结果与反求结果对比分析进行验证。
首先选择壳体上的全部16 个测点作为振动响应测点,采用激励反求载荷得到结果如表2。
从表2中看出,激励反求力远大于力矩数值,通过对比单独施加上述反求力矩和力的同点振动响应之比看,如表3所示,力矩只对切向振动有一定影响,激励反求径向力的作用远大于力矩的作用,结果讨论反求时,增加假设忽略力矩,只考虑反求径向力的误差。

表2 16点响应激励反求载荷

表3 单独施加反求力矩与反求力的振动响应比值
3.1 不同振动测试位置和点数对结果的影响
考虑到不同位置,包含不同角度和不同轴向高度对结果的影响,分为以下几个方案进行对比:

表4 不同响应点方案
各方案采用激励反求方法得到的激励力和力矩如图8和图9所示。以16 点反求结果为基准,各方案横向进行对比。另外,由于力矩数值很小,主要以激励力对比为主,力矩作为辅助对比。

图8 不同响应点方案反求激励力随频率变化曲线
从图8和图9中可以看出:
(1)反求激励力与16 点差异从小到大排序:方案1≈方案2≈方案4<方案3<方案5,其中,方案5的随频率变化趋势线与其他方案差异较大;
(2)不同方案反求激励力的最大力即130 Hz 激励力排序:方案5<方案2<16点(基准)<方案1<方案4<方案3,因所求得的激励力是要在空调系统上作为压缩机的激励源给管路系统的,故激励力比实际施加的稍大更合理,这样对管路系统的要求会稍更严苛,但也不能相差太大,以此为考虑,方案1 和方案4更合理;

图9 不同响应点方案反求激励力矩随频率变化曲线
(3)反求激励力矩与16 点结果差异从小到大排序:方案1<方案5<方案4<方案2<方案3,其中,方案3的力矩在高频运行频率下结果为负,完全不合理;
(4)综合以上各点,方案1(12个测点)是最接近16 点结果的,其反求的激励力误差在13%以内,力矩也是所有方案中与16点结果差异最小的,说明测点越多,包含各角度和主要位置的点越全,结果越准确;
(5)其他条件相同,角度不同方面对比,方案2(0度三点)与方案3(90 度三点)反求激励力结果分别处于16点结果的两侧,说明不同角度响应点反求激励力差异较大,基于此,采用同时包含0度和90度的方案4(0度2点、90度2点)反求激励力与16点误差在12%内,其也是除方案1(12点)外最合理的方案;
(6)其他条件相同,轴向高度位置不同对比,方案4明显优于方案5,主要原因是方案4采用的是上焊点和下焊点位置,而方案5 采用的是上焊点和静盘压缩腔位置,方案4 考虑了前文所提的两条主要传递路径,且两测点距离较远,包含的不同位置的特性更全;
(7)综上,在考虑角度和轴向高度位置及测点个数对结果的影响后,最终选择方案4(0度2点、90度2点)为最终激励反求测点。
3.2 只考虑径向力对结果的影响
因涡旋压缩机激励反求的力矩作用相对激励力来说非常小,故忽略力矩,只考虑径向力进行激励反求,结果如表5所示。

表5 激励反求时有无力矩对比
从表5看出,在其他条件不变的情况下,单径向力的激励力比力+力矩的力稍大,在运行频率80 Hz以上偏大10%以内,运行频率越低,误差越大。主要是因为涡旋压缩机主要由不平衡惯性力和切向气体力导致的轴向力矩导致,对于同工况压缩机来说,切向气体力导致的轴向力矩在不同运行频率下无变化,而不平衡惯性力则满足式(8),其与运行频率平方成正比,运行频率越高,不平衡惯性力越大,相对地其作用占比也越大。所以,低频运行时主要是力矩和力同时作用,高频运行时则是不平衡惯性力起主要作用,运行频率越高力矩的影响越小。

其中:m、r、ω分别为轴系总质量、轴系偏心量、压缩机运行圆频率。
对于空调系统中来说,涡旋压缩机管路运行应变问题主要出现在高频运行状态,故激励反求时只需要考虑径向力即可。亦即涡旋压缩机激励力反求时,最终方案为:单独施加径向力+方案4(上下焊点0、90度共4点)。
3.3 最终方案反求结果与试验结果对比(吸排气管)
采用单施加径向力的激励载荷反求方法求得已有运行频率测点的激励力的结果如图10所示。
图10中拟合曲线采用二次多项式拟合,与测点对应好,其变化特性与式(8)一致,力与转频的平方成线性关系,从侧面证明该激励反求方法的合理性。
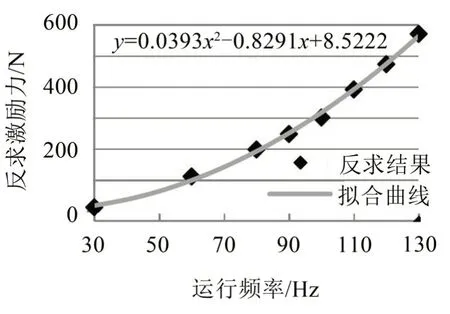
图10 运行频率范围最终方案激励力曲线
将采用单径向力反求的激励力施加在压缩机质心,通过频率响应分析仿真得到吸气管和排气管的振动位移,将其与试验测试的结果进行对比,如图11所示。从图11中可以看出:
(1)吸排气管振动位移随运行频率变化趋势仿真结果与试验结果一致,且排气管振动除30 Hz 测点外,其他与仿真结果误差在19%以内,吸气管则是仿真结果整体比测试结果偏大在28%以内,可能与反求激励力本身偏大有关,表5中可体现;
(3)吸气管仿真结果显示从30 Hz~60 Hz 间振动先减小后增大,主要是因为在33 Hz 以下压缩机减振胶圈系统固频对振动有放大作用,而试验时未测试该运行频率范围故未体现。
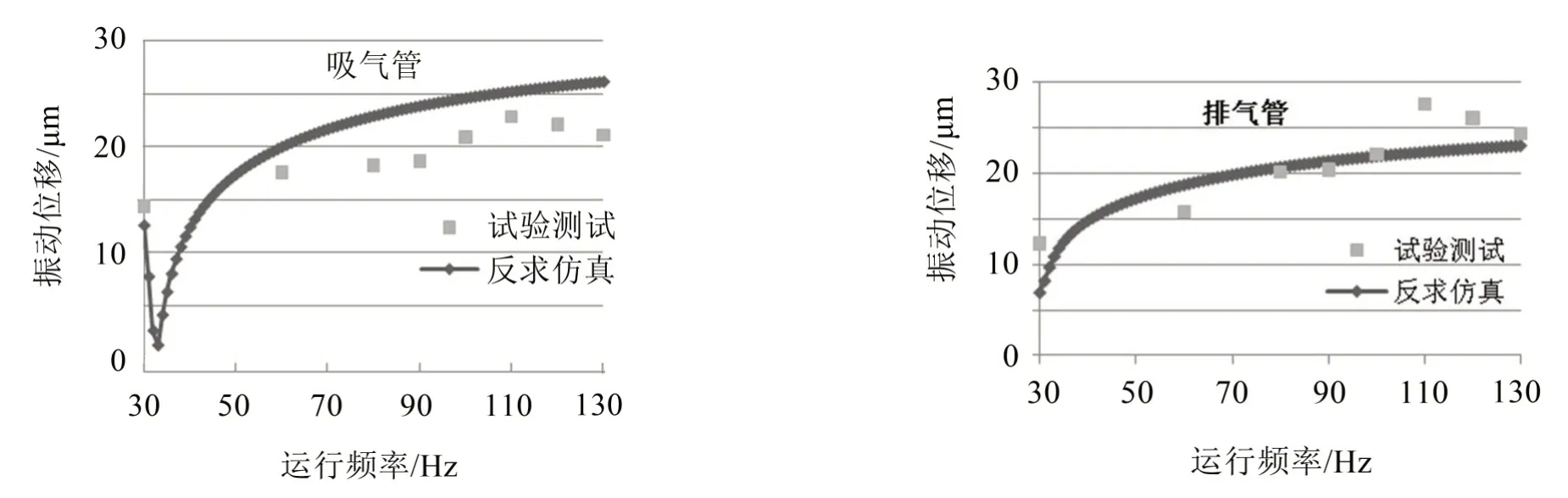
图11 吸排气管振动位移反求仿真与试验对比
4 结语
涡旋压缩机在匹配空调系统时,其振动会通过吸排气管对空调系统管路应力应变产生较大影响,为了得到对空调系统振动激励的大小,本文提出了通过振动位移响应反求涡旋压缩机激励载荷的方法,并对反求时振动响应测点位置、测点个数进行了分析与探讨,最终得到了某型号涡旋压缩机激励反求力和力矩的大小及添加方式。
结果显示,涡旋压缩机与转子压缩机有较大差异,其激励载荷主要以不平衡离心力为主,可忽略力矩的影响,且激励载荷与运行频率的平方成线性关系,运行频率越高,不平衡离心力越大。另外,以激励反求得到的结果为载荷,通过MSC频率响应分析仿真吸排气管的振动位移响应,将其与吸排气的试验结果对比,发现整个运行频率范围内结果一致性较好,验证了激励载荷反求方法的准确性。
