基于2.5维有限元-2.5维瑞利积分薄板声振性能研究

郎仕伟，邓铁松，圣小珍

(1.西南交通大学 牵引动力国家重点实验室，成都610031；2.上海工程技术大学 城市轨道交通学院，上海201620)

薄板是加筋板、层合板等复杂结构的基本单元，如高速列车组合地板中的外地板结构，在设计选材时，通常会考虑相同质量下隔声性能更好的材料[1]。因此，对薄板声振性能的研究有助于进一步了解和掌握各种复杂结构的隔声机理。

国内外学者针对薄板的隔声量做了一系列研究，Prasetiyo 和Thompson[2]建立了半无限薄板的声振解析模型，并调查了不同入射角度对隔声量的影响。Reynders 等[3]基于有限元-统计能量混合法，建立了空腔-板-空腔结构的薄板隔声模型，与实测结果的对比表明，其与传递矩阵法和波传播法得到的隔声量在中频吻合得更好。王笃勇[4]使用矩形管道模型，利用有限元软件ANSYS和Virtual.Lab Acoustics计算了无限大单层板和双层板的隔声量，并与波传递法得到的结果进行了对比。赵志高等[5]利用有限元-边界元法，分析了薄板声辐射功率与板厚以及激振力频率的关系；任亭亭[6]利用均匀分布法和周期结构分析法研究了无限大双层薄板的声学特性；霍新祥等[7]利用有限元声学软件ACTRAN得到了不同材料属性、几何参数及边界条件下矩形薄板在全频段的隔声量；黎胜等[8]还采用有限元-边界元法研究了平面声波由空气经加筋板向水中传播的特性。以上研究中，薄板为无限或有限结构，只能单一考虑结构的模态特性或波动特性。而组成列车地板、船舶船体、飞机舱体等的薄板单元，纵向尺寸远大于横向尺寸，可假设为无限长薄板，为典型的波导结构，在横向表现出模态特性，同时在纵向表现出波动特性。国内外学者对于这种无限长薄板声振性能的研究甚少。

2.5 维有限元法和2.5 维瑞利积分(2.5DFE-2.5D Rayleigh’s Integral)就是一种适合波导结构动力学分析的方法，最早用于预测轨道结构的动力学响应[9-10]，只需建立和求解截面的有限元模型，通过波动理论来表征位移场在垂直截面方向的传播规律，能有效克服传统有限元、边界元法在高频响应分析中的缺陷，提高计算效率。因此，本文基于2.5 维有限元和2.5维瑞利积分建立了无限长薄板声振模型，研究了结构的频散特性和隔声性能，讨论了入射角度、阻尼损耗因子和板厚对薄板隔声性能的影响，对由薄板单元组成的复杂板结构的减振降噪具有一定的理论指导意义。

1 2.5D FE-2.5D Rayleigh’s Integral理论

基于既考虑面内运动又考虑出平面运动的薄板理论和Hamilton 原理可得到2.5 维结构的振动控制方程[11]为

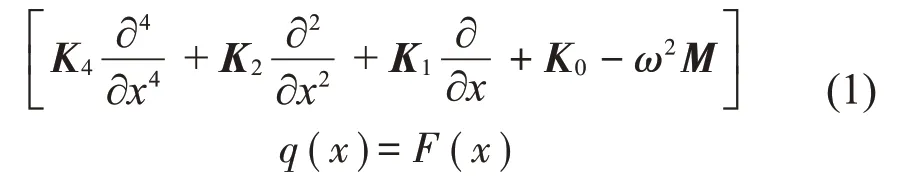
其中：q(x)为结构截面的节点位移列向量，若采用3节点2.5维壳单元，可表示为

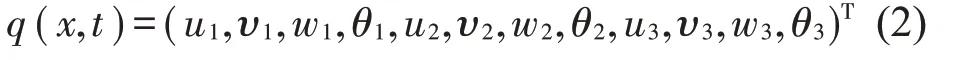
其中：ui和υi为节点的面内位移，wi为节点的出平面位移，θi为节点绕x轴的转动位移，矩阵Kn和M分别为刚度和质量矩阵，且矩阵K4，K2，K0和M为对称矩阵，K1为反对称矩阵，F为对应的节点力向量。对式(1)两边进行傅里叶变换得到波数域下的控制方程为

当波导结构与流体相互作用时，考虑三个耦合条件：(1)声压作用于结构；(2)接触面上结构的法向速度与流体法向速度相等；(3)将2.5D Rayleigh积分配置节点于接触面上。结构在力激励F~和声压激励条件下，通过上述三个条件可得到耦合系统的控制方程：

其 中：K=[(-iκ)4K4+(-iκ)2K2+(-iκ)K1+K0]，ρ0为流体密度；方程(4)对应第一个耦合条件，表示接触面上的声压作用于2.5维结构上的等效节点力；方程式(5)对应第三个耦合条件，和分别为边界节点的速度势向量和法向速度向量，n为边界的法向量，H和G是由2.5D Rayleigh积分配置节点时产生的矩阵为入射声压；方程式(6)对应第二个耦合条件，I为单位矩阵，C2为将有限元节点位移转换为边界节点位移的矩阵。

2 验证

本节中，以一块宽1 m、厚6 mm 的无限长薄板结合文献[2]的解析方法，就结构的频散曲线和隔声量验证了2.5DFE-2.5D Rayleigh’s Integral 的准确性。该薄板如图1所示，通过约束两端节点的平动位移实现简支约束，材料属性如表1所示。

2.1 频散曲线的验证

图1 无限长薄板的示意图

表1 薄板的材料属性

其中：ω为频率，κ为无限长方向波数。式(7)可通过给定频率ω得到特征波数κ或给定波数κ得到特征频率ω，从而得到薄板的频散曲线，如图2所示。并与文献[2]中的解析解进行了对比。

图2 无限长薄板的频散曲线

图2中波数为零时所对应的频率称为薄板结构的cut-on 频率（即二维截面平面应变问题的固有频率），具体值见表2。由表可知，2.5DFE 比文献[2]多出两阶cut-on频率，正好是薄板的前2阶面内波对应的cut-on频率。

2.2 隔声量的验证

平面声波斜入射至无限长薄板，入射角度按球坐标系定义，如图3所示，其中，夹角α和γ分别为方位角和仰角。

图3 平面入射波在坐标系中表示

在入射声波激励下，薄板的隔声量定义为

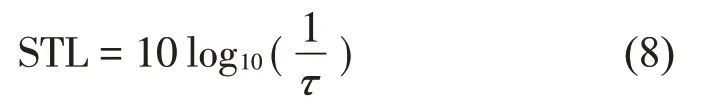
其中：τ是声功率透射系数，表示为

其中：Wtrans和Winc分别为无限长薄板单位长度透射声功率和入射声功率。入射声功率可表示为

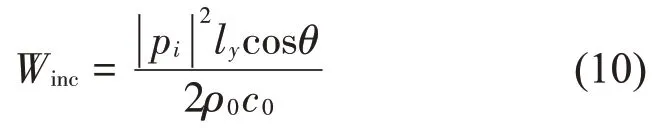
其中：θ为入射平面波矢量在薄板上投影与波矢量的夹角，可由入射角α和γ表示。透射声功率可表示为

为排除单元尺寸对隔声量的影响，确保模型验证的准确性，首先讨论了单元大小对薄板隔声的影响，如图4所示（声波以γ=90°、α=45°斜入射）。从图4可看出，在10 000 Hz以下，当在薄板1 m宽度内单元数大于30 时，其隔声量收敛；其它角度入射条件下，单元尺寸对隔声量的影响规律与该斜入射情况保持一致，不再赘述。因此，为提高计算效率，在后续的验证和计算中，薄板均按此单元大小进行网格划分。

声波以γ=90°、α=90°（即垂直薄板入射）斜入射时，本文隔声数值仿真结果与文献[2]的对比如图5所示。由图5可知，二者计算结果吻合很好；隔声低谷频率对应于无限长薄板的cut-on 频率（见表2），即图2中各出平面弯曲波频散曲线与y轴的交点频率。其它角度入射条件下，验证结果与该入射角度情况保持一致，不再赘述。

表2 2.5DFE和文献[2]的cut-on频率对比/Hz

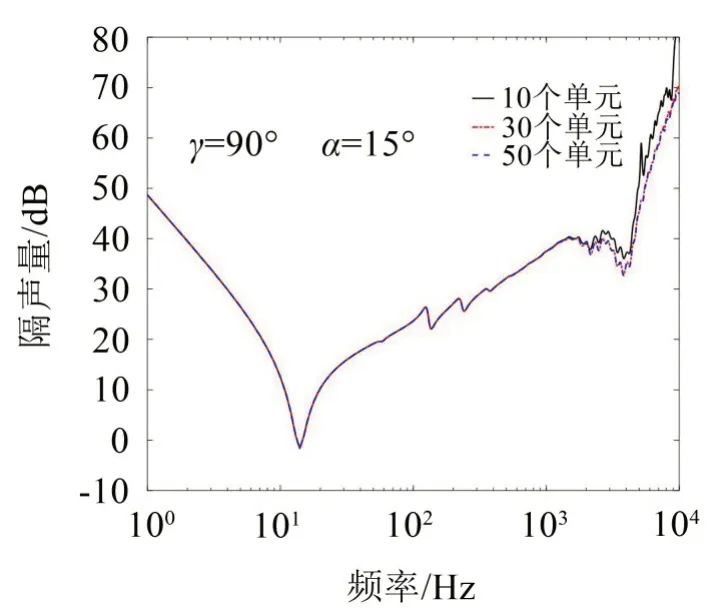
图4 当γ=90°，α=45°时，单元尺寸对隔声量的影响

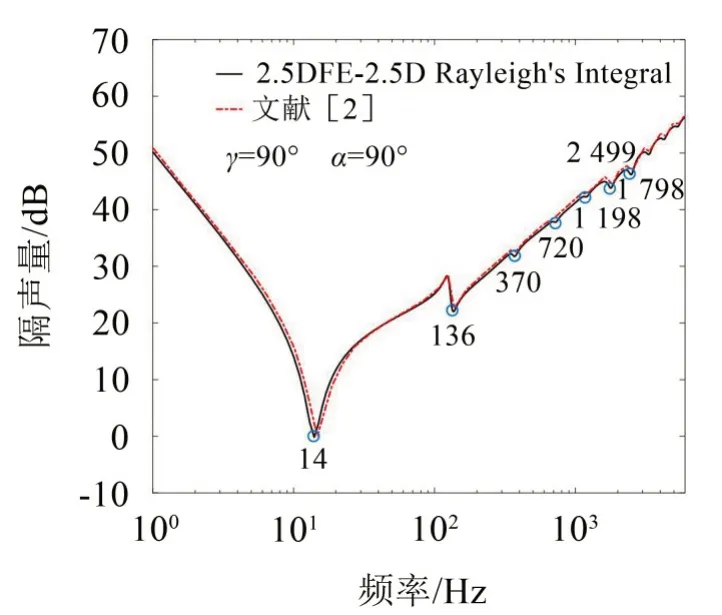
图5 当γ=90°、α=90°时，2.5DFE-2.5D Rayleigh’s Integral隔声仿真结果与文献[2]的对比

因此，结合频散特性和隔声的验证结果可知，本文建立的2.5DFE-2.5D Rayleigh’s Integral 模型是准确有效的，可用于无限长薄板甚至复杂波导结构的声振特性研究和减振降噪设计。

3 无限长薄板的声振性能

本节基于前面建立的2.5DFE-2.5D Rayleigh’s Integral 模型进一步研究前述无限长薄板的频散特性及波动特征，讨论平面声波入射角度、阻尼损耗因子和板厚对其隔声性能的影响。

3.1 频散特性及波动特征

无限长薄板的频散曲线如图2所示。每条频散曲线代表一种特征波在结构中传播。红色频散曲线代表出平面的弯曲波，在薄板横向表现出弯曲模态特征。例如，图6列出了图2中前3条红色频散曲线对应弯曲波的截面变形情况。

由于2.5DFE-2.5D Rayleigh’s Integral 模型中考虑了薄板的面内运动，其得到的频散曲线包括结构的面内波。例如，图2中红点1和蓝点2所在两条频散曲线代表薄板的面内波，其波动俯视图和截面变形如图7所示。由图7可知，面内波不发生面外位移，面内两方向位移耦合形成在无限长方向上传播的前2阶压缩波。

图6 前3阶弯曲波截面变形

3.2 入射角度的影响

以下研究声波分别沿无限长方向（α=90°）和沿横向（γ=90°）斜入射时，另一入射角对无限长薄板隔声量的影响，分别如图8和9 所示。由图8可知，最后一个较大隔声低谷频率为吻合频率，为入射声波频散平面内投影与平板第1阶弯曲波在高频处的交点频率，例如，当声波以α=90°、γ=20°入射时，图8和图9中圆圈标记处对应的频率；当入射角度γ增加时，吻合频率向高频移动，且吻合频率以下频带隔声量变大；除隔声吻合低谷频率外，其它隔声低谷频率对应薄板奇数阶弯曲波频散曲线与声波频散曲线平面投影的交点频率，例如，当声波以α=90°、γ=20°入射时，图8和图9中叉标记处对应的频率。这是因为，偶数阶弯曲波截面振型为反对称，其辐射声场在远场点处的声压趋于零。

由图10可知，当声波沿横向斜入射时，隔声曲线走势与声波沿无限长方向斜入射时相似，但曲线呈现更多峰值。这是因为，当声波沿横向斜入射时，整个耦合系统转化为二维平面问题，结构横向模态更容易被激发，隔声低谷频率对应图9中的cut-on频率。

3.3 阻尼损耗因子的影响

提高结构阻尼能有效抑制结构的振动，从而影响结构的振动声辐射和隔声规律，其对单一入射角度下和混响场隔声量的影响如图11所示。混响场隔声量定义为

图7 面内波的波形

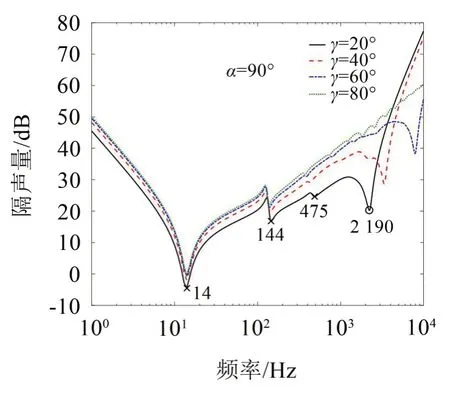
图8 当α=90°时，入射角度γ对隔声量的影响

图9 当α=90°、γ=20°时，声波频散面内投影与薄板

图10 当γ=90°时，入射角度α对隔声量的影响

其中：τd为混响场声功率透射系数，定义为

其中：θlim为积分下界角，取值依入射情况而定。本文计算时θlim取值为0°，积分取为2°。

由图11可知，隔声低谷附近的隔声性能受阻尼损耗因子的影响较大，随阻尼损耗因子的增加，隔声低谷周围的隔声量逐渐提高；此外，在混响场情况下，当频率高于临界频率（混响场隔声量最后一个明显低谷频率，即图中圆圈标记处）时，增加阻尼能大大改善结构的隔声量，其原因是把不同入射角的低谷都提高了。

3.4 板厚的影响

增加板厚既能增加板的质量，又能提高板的刚度，必将影响无限长薄板的隔声量。图12为薄板厚度由3 mm增加至9 mm，其对γ=90°、α=45°斜入射条件下和混响场隔声量的影响情况。由图12可知，薄板厚度对隔声曲线的刚度控制区、质量控制区及吻合频率之后区域均存在很大的影响。在刚度控制区，由于弯曲刚度随板厚增加而变大，隔声量相应提高；在质量控制区，由隔声的质量定律可知，当板厚或面密度加倍时，隔声量提高约6 dB；在高于吻合频率或临界频率的区域，隔声量随板厚增加而增加；由于薄板整体刚度随板厚增加而变大，导致隔声曲线“声学短路”区域（第1 阶低谷与吻合频率或临界频率之间的频带）缩小，图中圆圈标记处为吻合频率。

4 结语

本文基于2.5 维有限元法和2.5 维瑞利积分(2.5DFE-2.5D Rayleigh’s Integral)建立了无限长薄板声振模型，研究了薄板的频散特性及波动特征，同时，讨论了入射角度、阻尼损耗因子和板厚对隔声性能的影响，主要结论如下：

图11 阻尼损耗因子对隔声量的影响

图12 板厚对隔声量的影响

(1)无限长薄板在有限尺寸方向表现出模态特性，在无限长方向表现出波动特性，特征波包括面内压缩波和以横截面弯曲振型波动的弯曲波；

(2)随入射角度的增加，无限长薄板隔声吻合频率向高频移动，且吻合频率以下频带隔声量变大；

(3)增加薄板的阻尼损耗因子有助于提高隔声低谷附近频带及吻合频率之后频带的隔声量；

(4)增加板厚能有效提高无限长薄板在整个频段的隔声性能，隔声“声学短路”区域随板厚增加而缩小。

(5)该方法适用于复杂的无限长波导结构，在高频声振研究中，较传统有限元-边界元法计算的效率更高，具有广泛的应用前景。