基于同步压缩短时傅里叶变换的微型无人机识别*
2021-02-25孙延鹏屈乐乐
孙延鹏,赵 越,屈乐乐
(沈阳航空航天大学 电子信息工程学院,沈阳 110136)
0 引 言
近年来,微型无人机由于其简单易操控的特性在航拍、监测、农业和测绘等领域广泛应用,在带来便利的同时也引发了许多问题,如对空中交通管理的潜在威胁,以及无人机滥用引发的民事纠纷甚至刑事犯罪的概率也大大增加[1-2]。因此,出于增强无人机使用的规范性、保护人民群众的隐私及生命财产安全以及在禁飞区可以对无人机进行有效监测的目的,应对不同类型无人机进行精确地分类从而增强无人机使用的规范性。雷达具有全天时全天候工作的优势,在雷达目标识别中基于微多普勒效应的微型无人机分类是重要的研究方向。微多普勒效应指的是雷达检测物除平动多普勒频率之外因振动、旋转等微运动[3]而产生的额外频率调制的物理现象[4]。
近年来,微多普勒特征被应用于识别无人机领域[5-11]。文献[5]利用提取的微多普勒信号特征对微型无人机和空中鸟类进行识别。文献[6]提出融合多普勒图像的卷积神经网络进行无人机分类。文献[7]表明正则化二维复对数光谱分析可以用于提高无人机的识别率。文献[8-10]则提出利用多基地雷达对无人机进行分类,实验结果表明分类精度高于单基地雷达。文献[11]提出的节奏速度图(Cadence-velocity Diagram,CVD)分析不依赖于无人机的初始相位,极大提高了对多架微型无人机的检测能力。上述方法多是基于短时傅里叶变换(Short-Time Fourier Transform,STFT)得到信号的时频图像,但由于受到海森堡不确定准则的限制,导致时频聚集性欠佳,并且提取的时频图像特征均为单维度特征,描述的信号特征不够全面,影响无人机识别准确率。
不同于STFT的时频分析方法,本文采用同步压缩短时傅里叶变换(Synchrosqueezing Short-Time Fourier Transform,SSTFT)的方法进行雷达回波信号的时频分析。SSTFT是由Thakur[12]提出的一种时频分析方法,通过对短时傅里叶变换获得的时频谱进行同步压缩处理,令能量聚集到瞬时频率附近,有效提升了时频谱能量的聚集性。因此本文提出基于SSTFT的微动特征提取实现无人机分类识别,相较于常见的依赖短时傅里叶变换的识别方法具有更高的识别准确率。
1 实验设置及数据采集
实验采用K频段连续波雷达系统,载频24 GHz,基带采样频率128 kHz,发射功率16 dBm,天线增益15 dBi。
实验选用直升机、四旋翼无人机以及六旋翼无人机三种不同类型无人机,模型如图1所示。

图1 三类无人机模型图
实测实验时的场景图如图2所示。无人机与雷达传感器中心之间的初始距离为1 m,实际测量回波信号时每类无人机重复测量30次,每次6 s,共测得有(6 s)×(3类无人机)×(30次测量)=540 s数据。

图2 实测场景图
对雷达采集接收到的信号依次进行去均值及滤波处理,其中滤波器选择为低通滤波器,参数设置为通带截止频率5 kHz,阻带截止频率10 kHz,可以有效滤除信号中的噪声及雷达载波,在保留信号特性的基础上使信号平滑消减干扰因素。将每个测量的回波数据分割成18个分段,每段长度为0.3 s。在0.3 s时长内的数据点长度足以保证回波数据中可以包含若干个周期的雷达回波反射信号,确保可以获得精确的微多普勒调制参数。每一类无人机的数据总数为(18个分段)×(30次重复)=540。
2 基于微动特征的无人机分类
2.1 基于SSTFT的回波信号时频分析
对回波信号进行SSTFT时频分析可以获得与STFT方法相比能量较为集中的时频谱图,且该方法属于线性时频分析工具,不存在交叉项的困扰,有利于后续提取微动特征。
基于SSTFT的时频分析方法步骤如下:
雷达接收到的信号是待测无人机上所有散射点的回波,因此雷达接收到的微多普勒回波信号可以表示为[13]
(1)
式中:n是移动散射体的总数;ai是第i个散射体的反射系数;φi(t)=4πRi(t)/λ是第i个散射体的相位调制,λ为雷达发射信号的载波频率对应的波长,Ri(t)是第i个散射体距雷达的距离;η(t)为加性噪声。
首先对信号s(t)进行短时傅里叶变换,时频谱可表示为
(2)
式中:s(u)是雷达接收到的微多普勒回波信号,g(u)是短时傅里叶变换的窗函数,t是窗函数滑动的位置,ω是角频率。
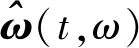
(3)
最后依据瞬时频率,对时频图进行重排,即同步压缩,可表示为
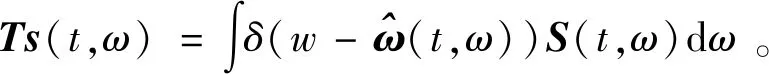
(4)
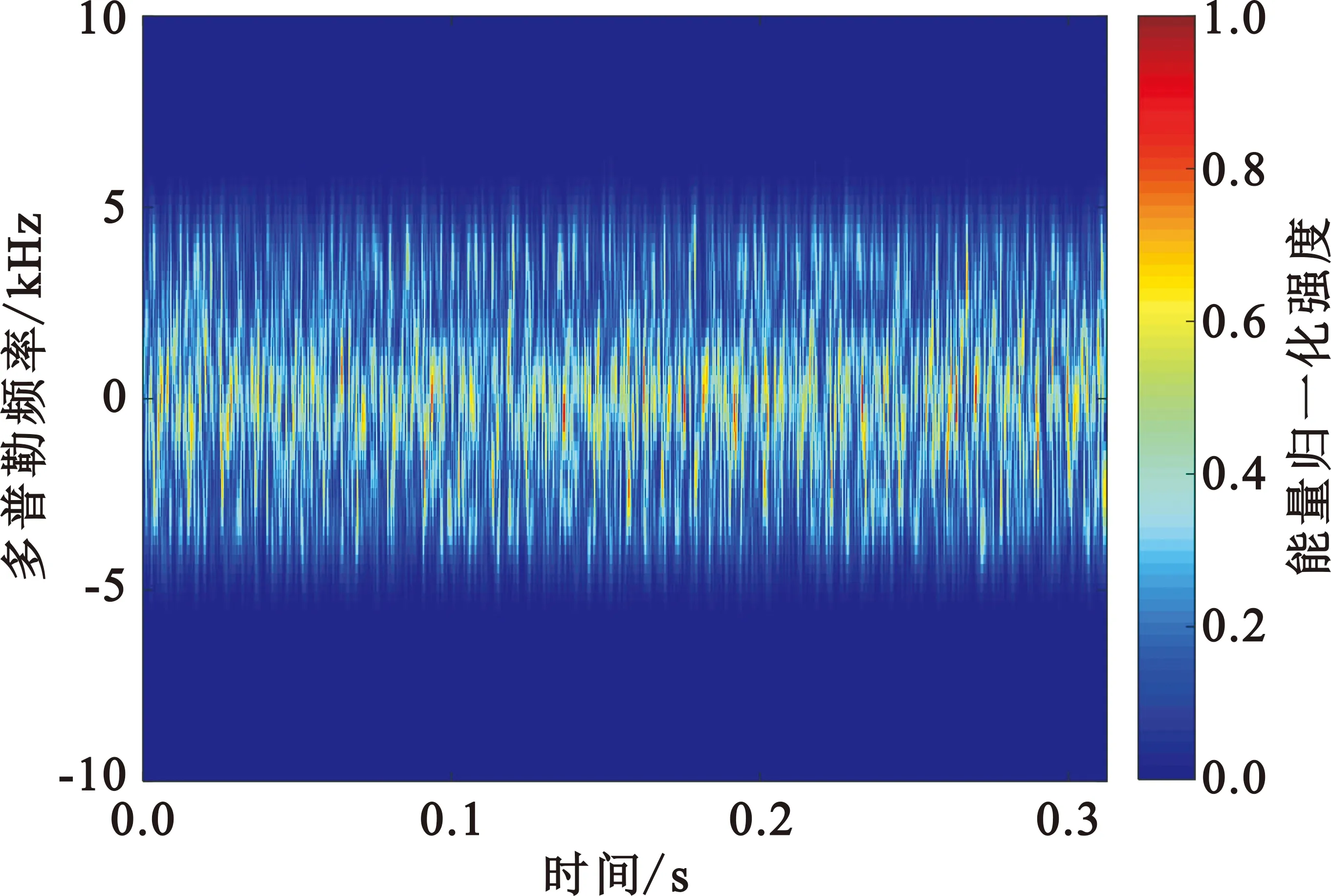
图3和图4分别为三种无人机的STFT和SSTFT时频谱图像。通过对比时频谱可以看出SSTFT的能量集中性优于STFT,尤其在采样时间较短的情况下,SSTFT时频谱的瞬时频率轮廓畸变明显小于STFT,并且具有更高的时频可读性,从而提高了所提取特征的准确性。从时频谱中可以更加直观地看出,不同微型无人机信号的时频图像形状和分布具有差异更加明显,因此采用SSTFT进行时频分析对于后续在时频图中提取有效特征用于微型无人机识别起到了关键作用。
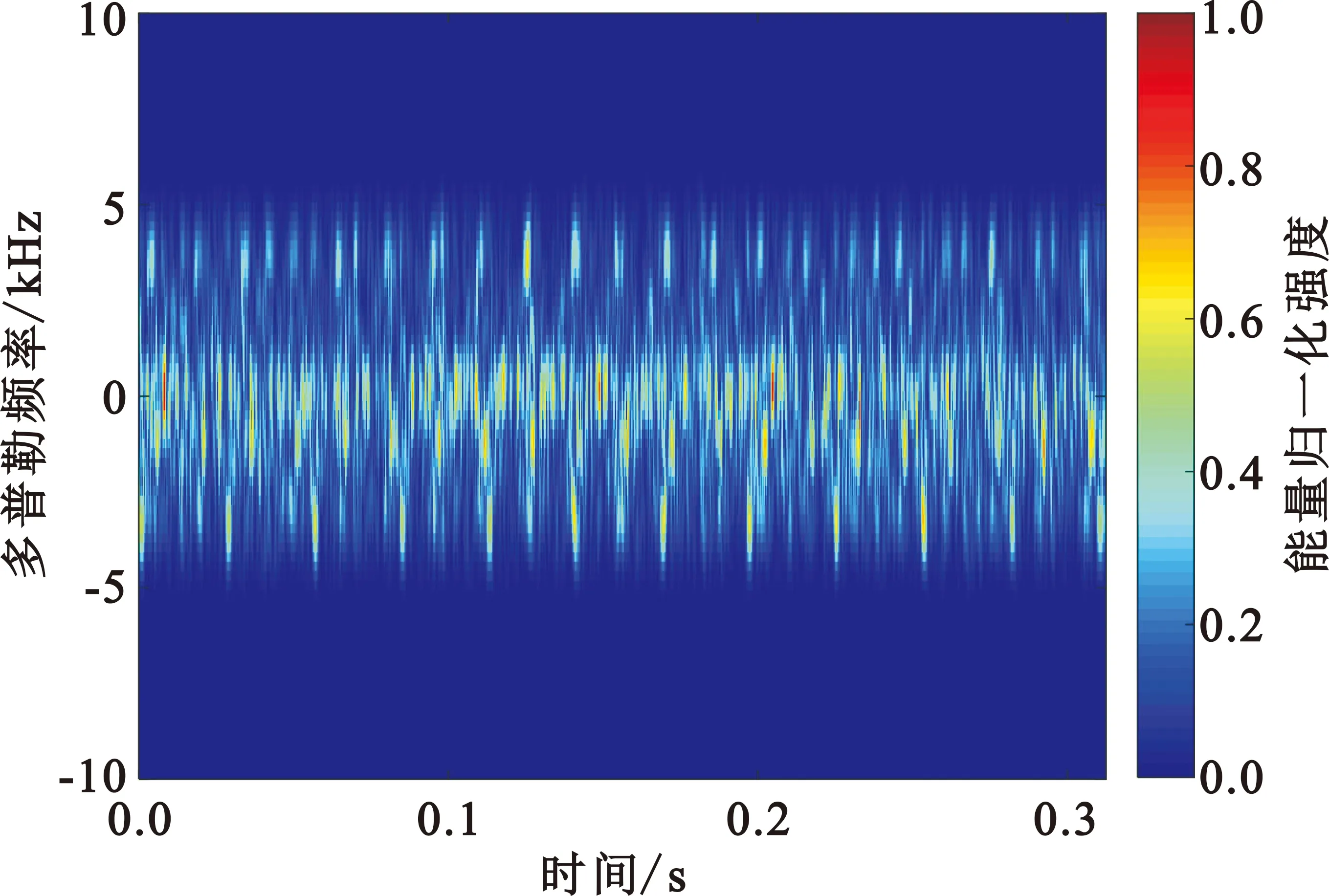
(a)直升机
(b)四旋翼
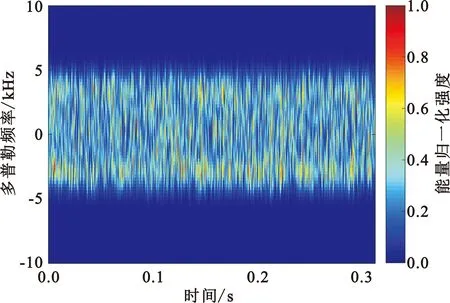
(c)六旋翼图3 三类无人机的STFT的回波信号时频谱
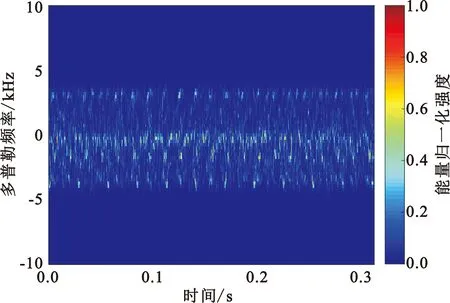
(a)直升机
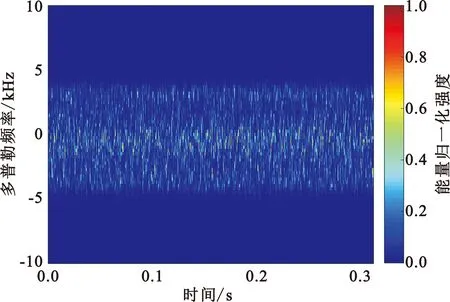
(b)四旋翼
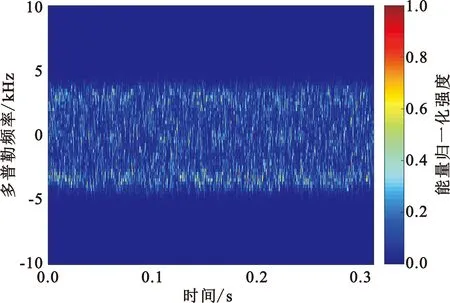
(c)六旋翼图4 三类无人机的SSTFT的回波信号时频谱
2.2 目标特征提取与选择
2.2.1 基于CVD提取频率变化特征
目前基于CVD进行目标检测和分类的文献只是提取能量最高的峰值和相匹配的速度特征作为特征向量[14]。文献[11]提出对CVD沿频率轴进行叠加得到节奏频率谱图(Cadence-Frequency Spectrogram,CFS)的提取方法,不依赖于旋翼的初始相位,是时间-频率谱图中多普勒频率周期特性的一般描述。因此本文提取CFS最高峰峰值位置以及去除峰值外的CFS的均方差结果作为频率变化特征,其中最高峰峰值的位置体现了旋翼的转速,均方差体现了频率变化的复杂程度,更加深入地描述了CVD的特征。CVD特征提取算法流程图如图5所示。

图5 CVD算法流程图
三类无人机的CFS处理结果如图6所示,可以看出三种无人机CFS结果两两不同。其中,四旋翼由于其具有较高的旋转速度,使得CFS结果的最高峰位置较远;而直升机由于其只具有一组旋翼,使得最高峰后的CFS结果平滑。通过最高峰位置及CFS结果的均方差,可以有效对旋翼进行分类。相较于只通过最高峰位置及所具有能量进行判别的方法,通过回波信号频率变化的复杂度及主频率大小,对于无人机种类可以更好地从其旋转特性上进行判别,其效果理论上明显优于利用旋转速度及回波能量等单一变量的识别。
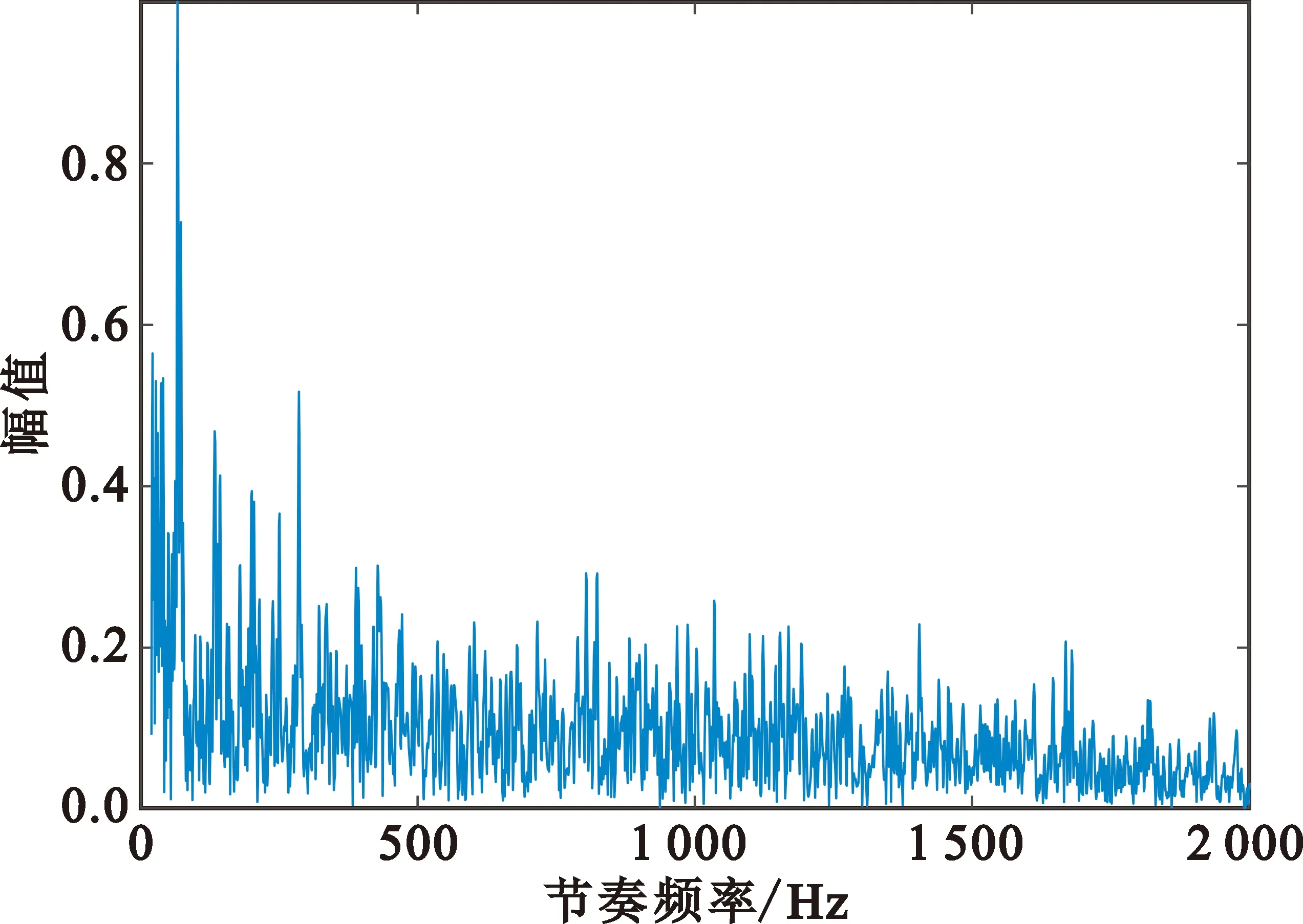
(a)直升机

(b)四旋翼
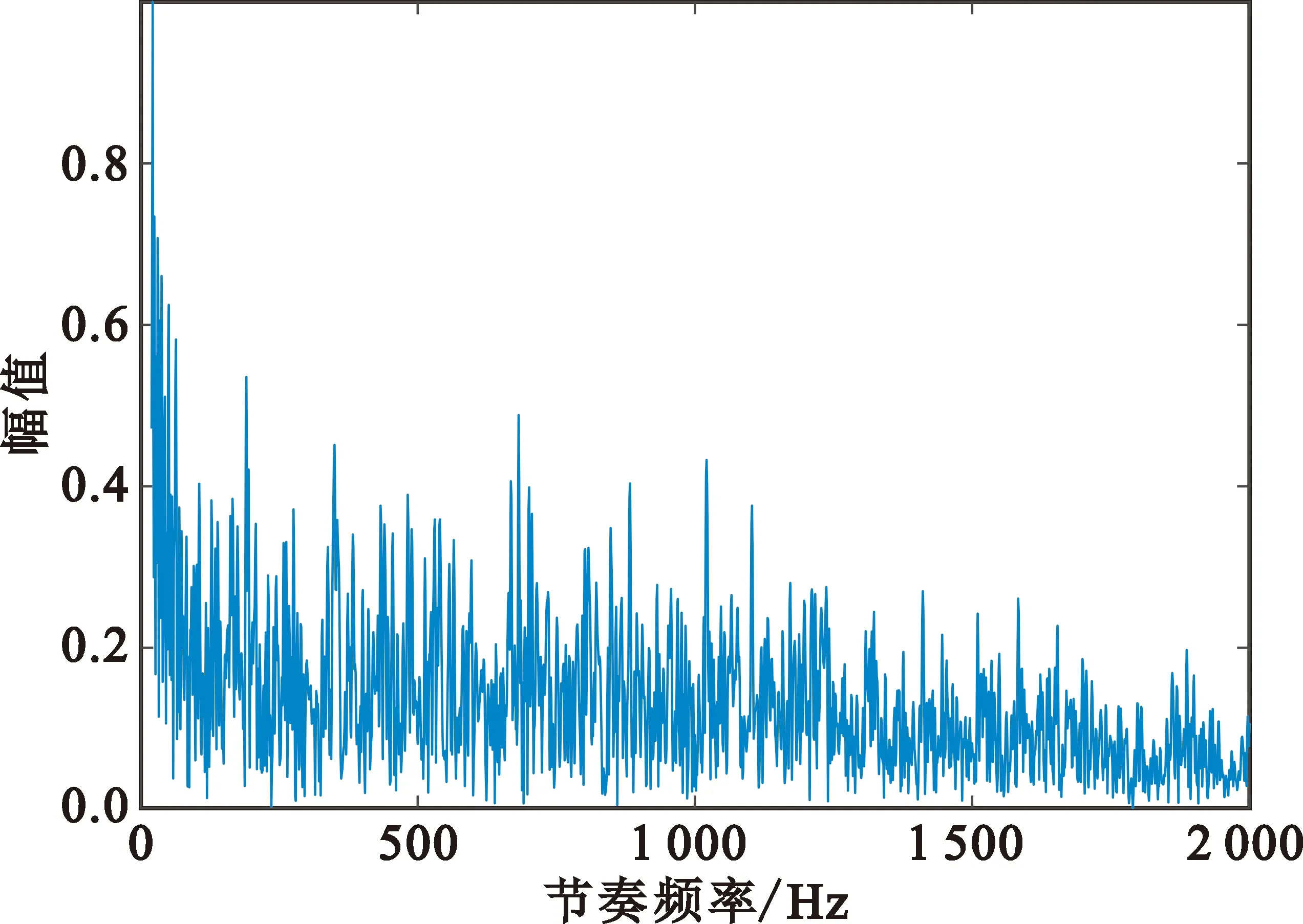
(c)六旋翼图6 三类无人机的CFS
但仅从回波信号频率变化的维度对旋翼进行分类存在一定不足,当无人机在加速或转向等状态的情况下,CFS最高峰位置可能出现变化,并且利用CFS结果均方差分析无人机旋翼数易受噪声干扰。因此,本文补充时频图的三维熵作为时频特征从多维度对无人机进行分类识别,获得准确率更高的识别方法。
2.2.2 基于时频图三维熵提取特征
在信号处理中,熵值的大小可以表示系统分布的有序性,进而反应信息量的大小。由于不同种类微型无人机旋翼数目的区别,导致时频谱分布均匀性存在差异。基于此种情况,通过香农熵反应时频谱离散程度,通过奇异值熵反应时频谱代数特征,通过范数熵反应时频谱能量的时间分布情况,利用三维熵可以完整表达时频谱能量分布、集中程度以及复杂程度。因此,可以将三维熵作为时频特征实现对不同类型无人机的分类。熵特征提取算法流程图如图7所示。

图7 熵特征提取算法流程图
将时频分布原始图像转换为灰度图像,采用维纳自适应滤波器去除灰度图像的噪声点,以改善图像质量。将图像处理后的时频图分块划分成n个子区域,ai(i=1,2,…,n)是时频灰度图中各个子区域的均值,时频图特征序列定义为A={a1a2…an},通过对A的不同计算获得三维熵。
(1)香农熵特征提取
香农熵又称作信息熵,可以作为时频谱复杂情况的度量。香农熵越大表示数据变量的不确定性越大,说明时频谱越复杂,无人机旋翼数目越多。
用n维概率矢量p=(p1p2…pn)来表示集合中各事件出现的概率,pi(i=1,2,…,n)满足0≤pi≤1且∑pi=1,则香农熵可定义为
(5)
(6)
式中:B是A的L1范数。
(2)奇异值熵特征提取
灰度矩阵中信息的相关性可以通过稳定性较高的奇异值表征出来。不同无人机的时频灰度图的奇异值大小不同,奇异值熵可以反映出时频图中旋翼的相关性,进而可以推测出旋翼数目,实现对无人机的分类。
将无人机的时频灰度图进行奇异值分解得到的奇异值λi(i=1,2,…,L)定义为时频灰度图的奇异值谱。依据信息熵理论,奇异值熵定义为
(7)
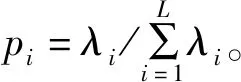
(3)范数熵特征提取
范数熵是对信号的能量分布进行定量描述的有效参数。由于
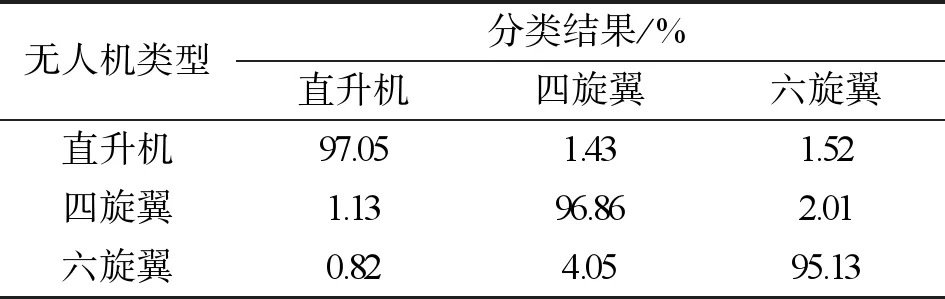
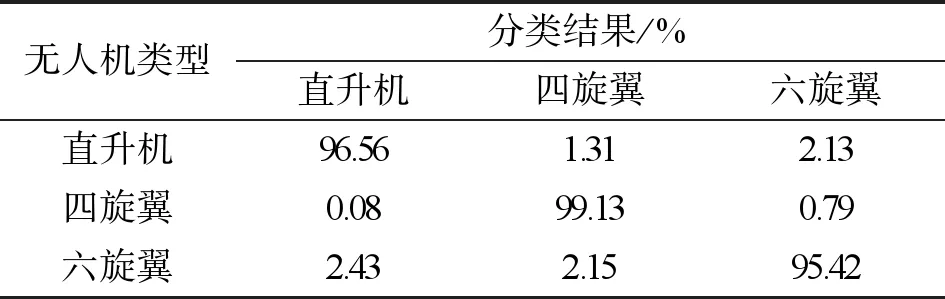
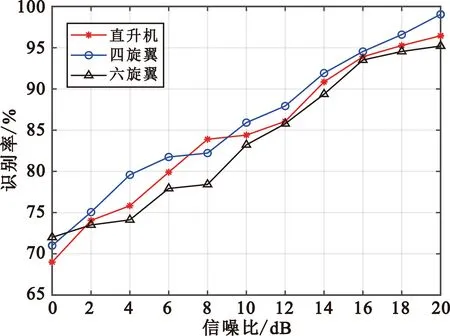
Ei=|ai|p,i=1,2,…,n,1 (8) 则范数熵可表示为 (9) 信号能量分布越分散,范数熵越大;反之,熵值越小。 在完成数据预处理及特征提取后,选择最适宜的分类器可以最大限度提高目标识别的正确率。本文选择SVM分类器对无人机类型进行识别分类。SVM分类器是基于结构风险最小原理和核技巧,通过将原始特征向量映射到高维空间从而进行分类。SVM分类器具有较强的泛化能力,并且由于其支持向量数目决定计算复杂程度,从而可有效避免“维数灾难”。 相较于现有识别方法的输入,本文分类识别过程中所采用的输入数据为多维度联合特征,该联合特征用一维向量x=(b1,b2,b3,b4,b5)表示,其中b1为CFS最高峰位置表示无人机旋转主频,b2为去除峰值外的CFS的均方差表示无人机旋翼复杂程度,b3为时频谱香农熵表示时频谱离散程度,b4为时频谱奇异值熵表示时频谱代数特征,b5为时频谱范数熵表示时频谱能量的时间分布。通过多维度特征联合的方式可以令SVM从多个维度对数据进行分类识别,降低干扰对识别准确性的影响,有效提高了系统识别能力。 将样本集X={x1x2…xn}与对应标签Y={y1y2…yn}输入到SVM中进行训练及应用。在SVM对数据集进行处理过程中,常用核函数有线性核、多项式核函数以及径向基核函数。在实际应用中当特征维数高并解决线性可分问题时选择线性核;多项式核函数多用于非线性且小数量级分类;而当特征数小而样本数目可观时常采用径向基核函数。本文识别时特征数目为5且样本数可观,选择径向基核函数作为SVM的核函数为最优,采用“一对一”训练方式来完成分类器训练。 综上所述,本文构建的微型无人机联合特征分类识别算法流程如图8所示。 图8 联合特征分类识别算法流程图 每一类无人机信号的数据总量为540,为评价该方法分类性能,随机选取每类信号的30%数据作为训练集,剩余70%数据作为测试集,通过训练及测试获得分类性能如表1~3所示。 表1 仅使用CVD特征的无人机分类结果 表2 仅使用三维熵特征的无人机分类结果 表3 联合特征的无人机分类结果 从表1~3可看出联合特征分类的结果优于仅用CVD或仅用三维熵特征分类的结果,这是因为联合特征是从多维度表征回波信号。因无人机初始相位的随机性受其旋翼位置的影响较大,而本文基于CVD提取的频率变化特征是不依赖相位的。但由于频率变化受环境噪声的影响,因而会降低分类的准确率。引入三维熵后,由于三类无人机的旋翼数量不同,使得微型无人机的时频谱分布不同,三维熵从不同方面对三类无人机的时频谱分布复杂度进行定量描述,因此联合特征提高了微型无人机分类的准确率。 从表3中数据可以看出,六旋翼的识别错误概率最高,直升机的识别能力也存在一定的劣势,主要原因是由于直升机与六旋翼的旋转主频十分接近,在环境噪声强度较高而三维熵特征不十分明显的情况下,导致识别出错率更高;并且四旋翼和六旋翼的频率变化复杂程度较为接近,导致六旋翼在依靠CVD特征时的识别效果较差。由于直升机的时频谱分布相对另外两者而言较为集中,使得四旋翼和六旋翼在依靠三维熵进行识别时识别率较低。在未来的研究中可以采用深度学习方法,对无人机进行分类识别。通过计算机自主提取特征,避免手动筛选特征导致的特征不全从而影响识别能力。然而,利用深度学习进行分类的方法分类速度相对较低,需进行适当考量。 通过在不同信噪比下对所提方法进行识别能力测试,验证方法的识别性能。将雷达接收到的信号与高斯白噪声进行加性混合,信噪比定义为信号与噪声之比,即 SNR=10lg(P(s)/P(n)) 。 (10) 式中:P(s)和P(n)分别表示信号平均功率及噪声平均功率。 在30%训练样本条件下,将信噪比范围设置为0~20 dB,步进为2 dB,每一信噪比下均采用200次蒙特卡洛实验,由此得到的微型无人机平均识别率如图9所示。 图9 不同信噪比下三种无人机识别率 由图9可以看出,在信噪比大于14 dB时,无人机的识别率可以保持在90%以上。这是因为本文利用SSTFT算法获得时频谱,由于算法压缩特性,面对噪声干扰可以有效在压缩过程中将其能量消减,从而降低噪声对信号处理及特征提取过程的干扰。 为了进一步说明本方法的优越性,在同等条件下,将本文所提方法与文献[10]和文献[11]方法进行对比,对三种无人机的平均识别率实验结果如表4所示。 表4 实验结果对比 表4说明了本文所提方法在识别准确率上有了一定的提高。文献[11]中CFS的最高峰值及位置受噪声的影响比较大,K-means分类算法对噪音和异常值比较敏感;文献[10]中时频分析方法的时频分辨率不高且利用主成分分析提取的特征不能够完整地表述信号的有效信息;而本文所提方法利用SSTFT可以得到更精确的时频表达,从多维度提取有用特征信息,从而更有利于后续无人机的分类。 本文基于SSTFT提出了一种新的特征提取方法用于微型无人机分类。基于实测回波信号的实验结果表明,采用SSTFT提高了数据处理过程抗噪声性能,并从不同维度进行联合特征提取进一步提高了微型无人机分类的准确率,可达到97.03%。在下一步工作中,将增加对八旋翼以及多架无人机同时出现的分类研究,以使该算法拥有更为广阔的应用前景。2.3 SVM分类识别

3 实测数据结果分析
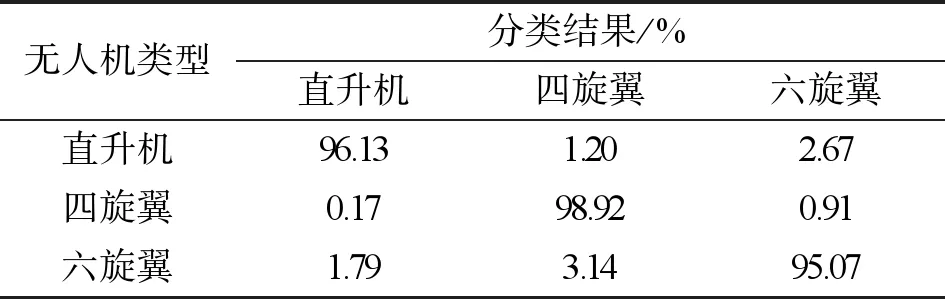
3.1 不同噪声水平下的识别率分析
3.2 不同算法对比的识别率分析

4 结束语
