基于贝叶斯框架下大坝服役性态综合评估方法

张 涛，苏怀智

(1.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学 水利水电学院，南京 210098)

1 研究背景

水库大坝是我国国民经济的重要基础设施，在防洪、发电和航运等方面上发挥着巨大作用[1]。目前我国已经建成水库大坝9.8万余座，是世界上水库大坝最多的国家[2]。

大坝面临着自然气候变化、运行条件复杂等风险作用，对大坝服役性态的综合评估和决策管理提出了较高的要求[3]。大坝服役性态受多种随机性因素的影响[4]，其在服役过程中受到环境(气温、降水等)、荷载(水压、自重等)及突发性灾害(洪水、地震等)等外部因素的共同作用[5]。另一方面，位移、应力及渗漏等时变量的非线性、非稳态性特征也是大坝性态的集中体现[6]。总而言之，如何厘清随机性因素之间的关系，挖掘其中的关键影响因素并判别影响程度，从而更全面、有效地进行分析和评估，对大坝健康服役具有重要意义。

大坝服役性态的评估一直是坝工领域的热点问题。例如，吴中如[7]运用模糊理论及数理统计，对大坝服役性态进行了有效地评估；苏怀智等[8]基于广义帕累托模型以超限测值样本代替极值样本拟定了大坝性态的预警指标；王子敬[9]基于多种概率分布对大坝服役性态进行估计并将结果进行对比。近年来，随着计算机技术的发展和机器语言的广泛使用，各种新的模型相继出现。Su等[10]提出结合证据理论和集对理论，融合多源时空信息的性态诊断模型；胡江等[11]将MF-DFA(多重分形消除趋势波动分析)方法应用在大坝安全监测序列分析和整体性态评估中；游健等[12]提出了基于改进层次分析法的大坝性态安全诊断云模型。大坝服役性态是一个复杂多变的过程，现有模型存在轻主观经验重客观数据的现象，仅限于数据的机器学习方法容易过拟合。另一方面，大坝工程是人类经验不断累积的结果，经验的融入更能挖掘数据中无法体现的隐性变量，优化复杂评估体系。

贝叶斯网络是最近几十年发展起来的系统建模方法，是一种系统地描述随机变量之间关系的语言。其基本的思路是将人们的经验知识作为先验信息融合到实际模型中，即综合利用模型信息、数据信息及先验信息来进行分析评估，是一种专家主观经验和客观定量分析相结合的评估方法。贝叶斯网络已广泛应用于工程的风险诊断和性态评价之中。程江洲等[13]基于贝叶斯框架描述了水力发电系统间复杂关系并进行动态风险评估；刘阳等[14]基于模糊理论与支持向量机理论分别从主客观评估边坡地震失稳规模；杨咪等[15]提出的基于熵权的贝叶斯模型在水质评价中的得到了应用。贝叶斯网可以把复杂的评估体系分解成一系列相对简单的模块，从而大大降低了大坝性态评估的复杂性。此外，贝叶斯网络是概率论和图论相结合的产物，通过节点和节点间有向弧(因果关系)，可以探究大坝系统中各失效模式之间的串联、并联及串并联关系，并构建具有多失效模式的大坝性态评估模型。贝叶斯网络节点是由随机因素组成，每个随机因素的时间序列又充分考虑了因素的时变性。因此，基于贝叶斯框架下大坝的综合评估方法能够有效地融合主客观知识，厘清各种随机因素之间的关系，考虑各因素的时变特性。与此同时，也给出了失效概率等级划分及处理方法，是一套全面且系统的评估模型。

2 大坝服役性态综合评估方法

基于贝叶斯网络框架的大坝服役性态评估方法主要包括明确网络结构、确定失效概率、评估结果及分析3个方面。①贝叶斯网的构建是进行大坝性态分析与评估的基础环节。其主要通过朴素贝叶斯分类器并结合实际经验将大坝按失效路径确定评估指标，再用贝叶斯信息准则(BIC)评分[16]进行修正，得到优化的网络结构。目的在于挖掘大坝运行过程中潜在的影响因素及其串并关系。②失效概率的确定是框架的核心部分。其主要通过模糊综合评价理论[17]确定先验概率，再用熵权法[18]确定各指标条件概率，最后运用贝叶斯估计模型进行概率推理，确定失效的后验概率。③评估结果分析主要从主观与客观、整体与部分、静态与动态3方面说明了结果的有效性，同时依据失效概率划分的评估等级表[19]，对大坝的服役性态进行评估定级并提供安全决策。

2.1 确定服役性态评估网络结构

为了大坝服役性态评估网络结构表现更直观，采用朴素贝叶斯模型。朴素贝叶斯模型是一个包含一个树节点和多个叶结点的树状贝叶斯网。如图1所示，树节点是失效指标，叶结点是随机变量。

图1 朴素贝叶斯分类器Fig.1 Naive Bayesian classifier

通过贝叶斯信息准则(BIC)评分对网络结构进行修正。基本思想是在依据最大似然估计附近把对数似然函数展开，然后将计算转化为一个多元正态分布函数在极值点的邻域积分，具体表达式如式(1)。

式中：Δ为网络结构；D为实测数据样本；θ*为参数向量θ的最大似然估计；参数向量θ由d个独立参数构成；m为样本量。

式(1)中右边第1项度量结构与数据的拟合度；第2项是模型复杂度的罚项，避免产生过拟合。根据经验确定指标网络，结合BIC评分对网络结构的优化，确定最终的大坝服役性态评估网络结构。

2.2 确定服役性态评估网络参数

大坝服役性态评估网络参数包括2部分，即失效的先验概率分布和条件概率分布。

2.2.1 先验概率分布

先验概率分布采用模糊综合评价方法来确定，主要步骤如下。

(1)获取评估语言：针对待评的大坝，搜集影响其性态的因素，并根据具体情况将各因素划分为若干等级，给出评估等级集，即备择集M。根据文献[20]建议将评语等级设为安全(M1)、较安全(M2)、中等(M3)、较危险(M4)、危险(M5)5个等级，备择集如式(2)。

M={M1,M2,M3,M4,M5} 。

(2)

(2)确定模糊隶属函数：专家经验的评估语言，需要转化为数学语言，这里用到的是模糊隶属函数的概念，用模糊隶属函数映射评估语言。具体隶属函数如式(3)所示。

(3)

式中：U(x)为三角形隶属函数；a,b,c为参数，视不同的评估语言而定，如“安全(M1)”评语时a,b,c分别取0,0.2,0.4，依次类推。

(3)确定模糊概率：模糊概率的确定采用最值设置法[21]。根据图2得到左、右有效数为：

图2 最值设置法示意图Fig.2 Schematic diagram of setting maximums

PR(Z)=sup[U(x)∩Umax] ；

(4)

PL(Z)=sup[U(x)∩Umin] 。

(5)

式中：PL(Z)为左有效数；PR(Z)为右有效数。

由式(4)、式(5)计算模糊概率PM为

PM=(PR+1-PL)/2 。

(6)

为了平衡不同专家评估结果的差异性，根据具体情况设定权重集ω，即得到加权后的模糊概率。

通过Onisawa公式[22]将加权后的模糊概率转化为失效的先验概率Pc,k为先验概率指数，PM为模糊概率。

(7)

(8)

2.2.2 条件概率分布

条件概率分布是大坝性态失效指标与随机变量之间条件概率关系网络，描述各随机因素之间影响程度。本文使用熵权法求解，其计算步骤如下。

(1)建立m个随机变量，n个指标的判断矩阵，即

R=(rij)m×n；

(9)

(2)归一化处理得到归一化矩阵，即

B=(bij)m×n。

(10)

(3)确定大坝性态失效指标的熵为

(11)

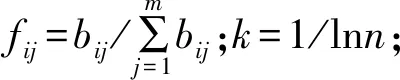
(4)大坝性态失效指标的熵权为

(12)

(5)各叶节点(随机变量)对树节点(失效指标)的影响采用熵权法确定权重。指标值与实测值之间的权重应用几何概率的概念，采用距离法，用代表指标与所选变量标准之间差值绝对值倒数进行计算，即

(13)

式中：Lij=|i-j|(i,j=1,2,…,4)。

根据式(9)—式(13)求得条件概率网。

2.2.3 风险推理

对于大坝服役性态评估贝叶斯网络N=(Δ,θ)，认为θ为随机变量，关于θ的专家经验知识表示成先验概率分布P(θ)。再经过客观实测数据D=(D1,D2,…,Dn)影响后，用似然函数L(θ|D)来归纳，根据贝叶斯估计有

根据上述分析过程，得到兼顾专家经验和实测数据的失效概率。

2.3 大坝服役性态评估等级划分标准

根据相关文献，对失效概率进行等级划分，具体如表1所示。根据评估等级，确定大坝的服役性态情况并采取相关措施。具体如下：1级，可以正常服役；2级，需要实时监测，定期维护；3级，需要采取相关措施降低风险，避免风险持续上升；4级，风险可能发生，需要实时排险维稳；5级，加大检修力度，做好预警准备。

表1 失效概率等级划分Table 1 Rating of failure probability

3 大坝服役性态评估实现流程

依据贝叶斯理论框架，对大坝服役性态评估实现流程主要如下。

步骤1:利用结合经验的朴素贝叶斯分类原理及BIC评分优化，确定贝叶斯网络结构Δ。

步骤2:利用模糊综合评价理论确定基于专家经验的先验概率P(θ)。

步骤3:统计随机变量的相关参数，结合熵权法原理，得到基于客观实测数据的条件概率网L(θ|D)。

步骤4:利用贝叶斯估计确定失效的后验概率P(θ|D)。

步骤5:根据失效概率划分等级，评估服役性态。

具体贝叶斯框架如图3所示。

图3 大坝服役性态的贝叶斯框架Fig.3 Bayesian framework of dam service behavior

4 工程案例

某水库枢纽工程由拦河坝、泄洪隧洞、溢洪道、发电引水钢管和发电厂房等建筑物组成。拦河坝为混凝土双支墩肋墩坝(又称大头坝)。坝顶轴线长度331 m，坝顶宽度4 m，最大底宽72 m，坝顶高程204 m，防浪墙顶高程205.2 m，最大坝高83.1 m。该工程竣工于1960年，存在的问题主要有：防洪标准低，不能满足规范要求；大坝基础变形较大，存在贯通上、下游的断层和裂隙，透水性大；坝垛裂缝严重，削弱了垛墙的整体性，恶化了垛墙的应力状态等。

4.1 综合评价网络结构

本文根据该坝监控实测数据选择了水位差X1、降雨量X2、气温差X3、坝前水温X4、纵向水平位移X5、横向水平位移X6、垂直位移X7、地基沉降X8、裂缝宽度X9、地下水位X10、渗流量X11、坝体温度X12、锚索应力X13、钢筋应力X14，共14个随机变量。根据专家经验分成4个指标，分别为环境量Y1，变形指标Y2，渗漏指标Y3，应力指标Y4。并用BIC评分结果调整，具体的网络结构见图4。

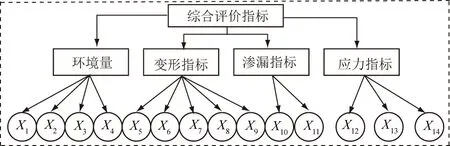
图4 综合评估的贝叶斯网络Fig.4 Bayesian network for comprehensive evaluation

4.2 综合评价网络参数

4.2.1先验概率分布

根据模糊函数综合评价模型确定随机变量的先验分布。对于不同的随机变量，以专家的评估语言作为样本的输入。

以地基沉降X8为例(其它变量类似)，选择4位专家的评语M=(M1,M1,M1,M2)，权重ω=(0.3,0.3,0.2,0.2)。由式(3)—式(8)可计算出失效的模糊概率PM=0.216 7，先验概率Pc=0.000 294。对X1—X14都进行上述过程，获得失效的先验概率如表2所示。

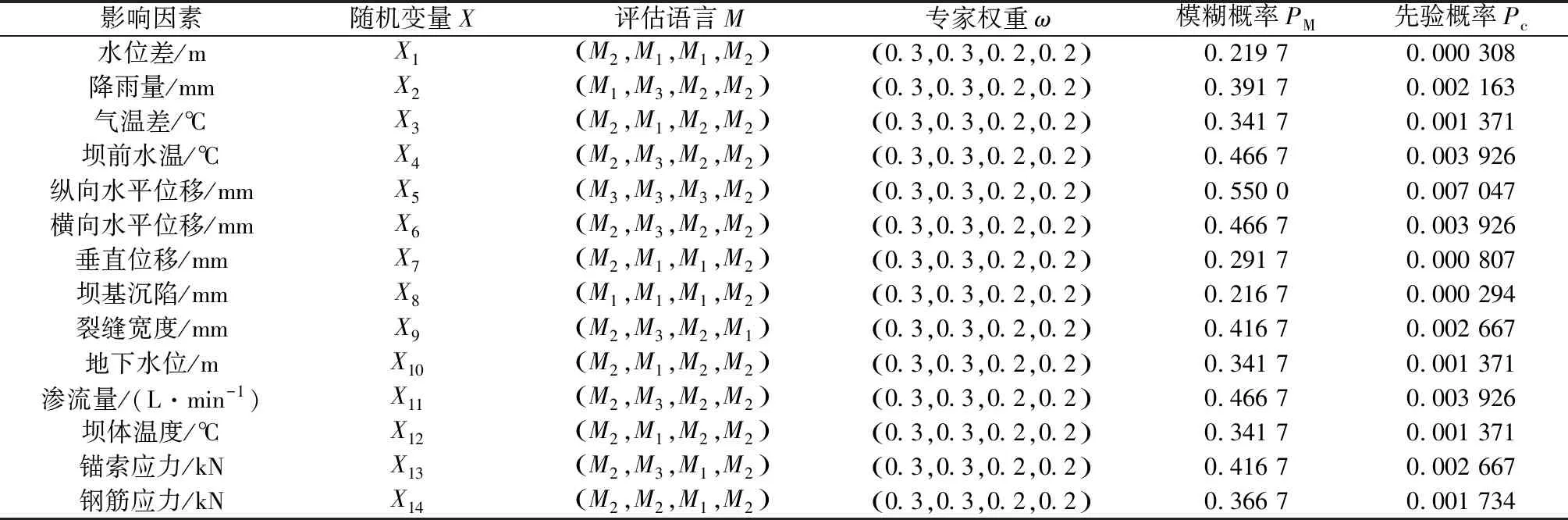
表2 评估语言与先验概率Table 2 Evaluation language and prior probability

4.2.2 条件概率分布

图5 某混凝土坝地基沉降测点分布Fig.5 Layout of measuring points for foundation settlement of a concrete dam

对于X1—X14这14个变量均采用此方法，计算结果如表3和图6所示。根据熵权法和距离权重法，求得条件概率表(CPT)。具体结果见表4和表5。

表3 变量及样本统计Table 3 Variables and statistics of samples

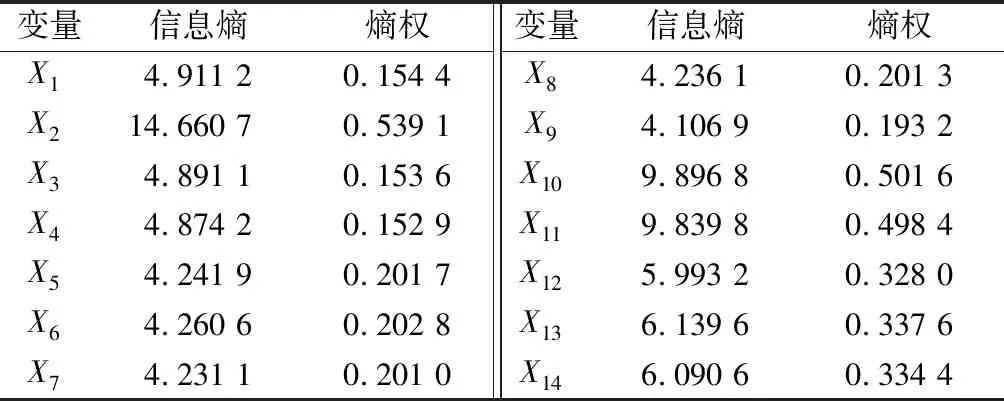
表4 指标的熵及熵权Table 4 Entropy and entropy weight of indicators

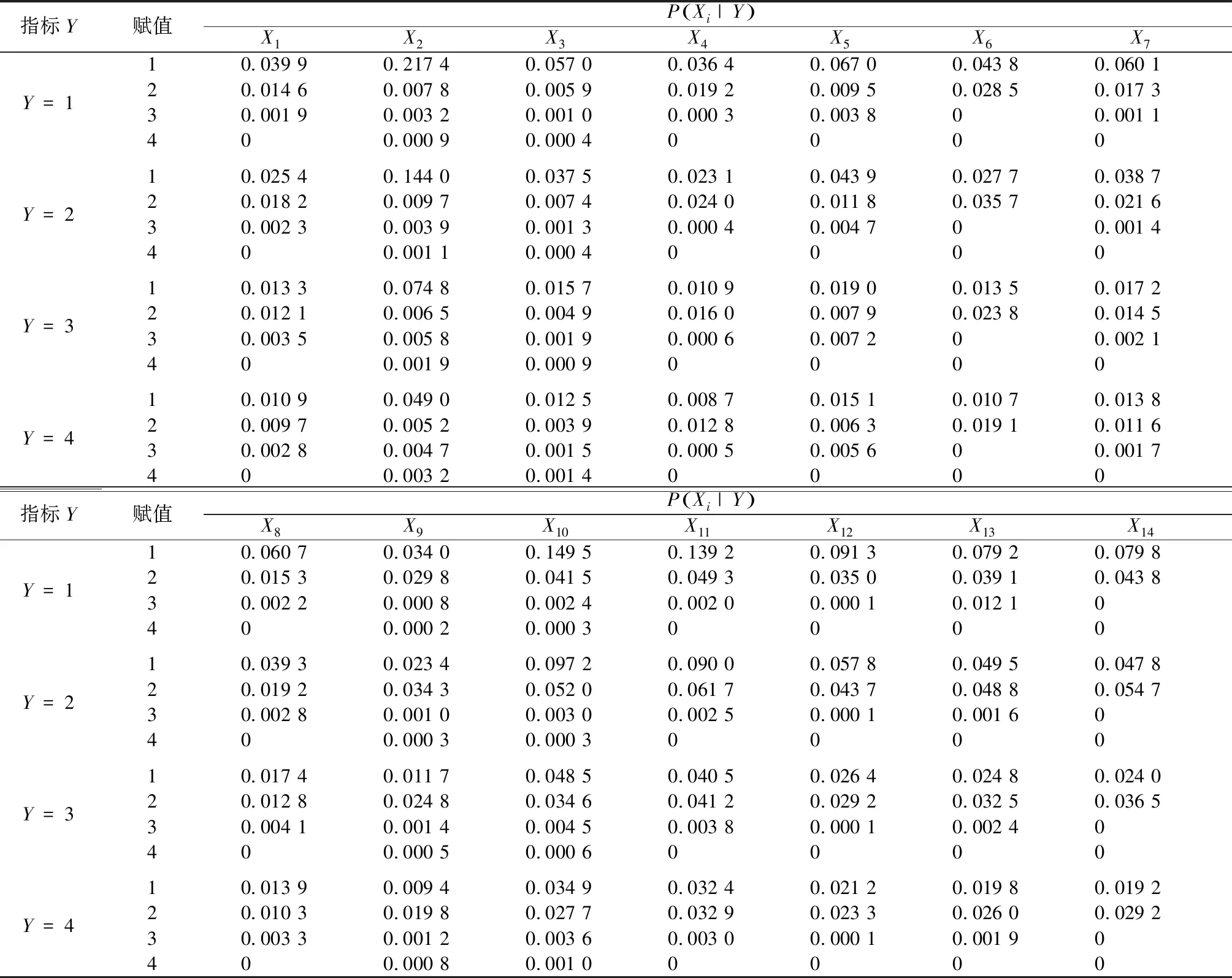
表5 条件概率Table 5 Conditional probability

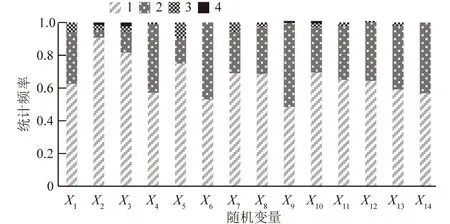
图6 随机变量偏移统计Fig.6 Statistics of random variable migration

4.3 评估结果

4，5)。由于无法明确客观经验和实测数据所占比重，这里视为同等重要。根据表2的先验概率和表5的条件概率可以得到各个指标的失效概率。结合失效概率等级表，得到的选择指标等级如表6所示，对于不同的等级相应采取不同的决策措施。对于不同指标赋予不同权重，这里简化成4个指标影响程度均等，这样可以从宏观上定性判断此混凝土坝所处的服役性态。

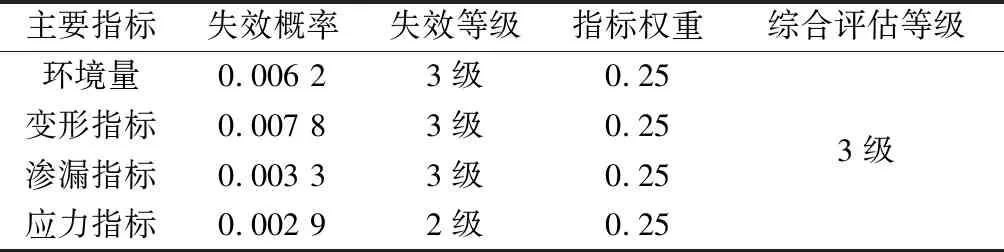
表6 主要指标的风险等级Table 6 Risk levels of major indicators

4.4 结果分析

4.4.1 主观与客观相结合

简化了相关性不强的随机因素，运用BIC评分优化结构能够充分考虑样本数据的特性。基于专家经验的模糊评价理论，能够挖掘数据中的隐变量，以先验概率量化专家的模糊语言。

由表2专家经验结果可以看出：坝体纵向水平位移的失效概率最大，横向水平位移和渗流量次之，说明水平位移和渗流是专家先验评估较危险的随机因素。另一方面，依据实测数据的生成的条件概率表使得贝叶斯推理完全按照概率论进行，具有客观性。

由表4及表5可知降雨量对大坝影响较为明显。虽然两者得出的结论不一致，但是换个角度考虑更有其道理，由于降雨量的输入才导致位移的开展和渗流的加剧。专家经验着重现象，实测数据着重原因。

4.4.2 整体与部分相结合

基于贝叶斯框架大坝服役评估方法，从整体上来看，能够融合该混凝土坝多测点、多随机因素的时间序列。将各指标下的失效概率按权重求和即可以得到综合评价指标，根据结果可以整体上了解大坝的服役性态并给出相应的决策。

由表6可得到此混凝土坝安全等级为3级(需要采取相关措施降低风险，避免风险持续上升)。另一方面，依据失效概率表达的各种随机因素能够清晰地反映各级失效程度，有助于找出主要失事路径。例如环境量中的降雨量造成失效概率较大，这与安全鉴定结果中采取设置更高的防洪标准，增加溢洪道的泄流能力等措施相一致；又再如变形指标的失效概率较大，与鉴定报告中加强变形的监测，控制坝体及坝基裂缝，避免库水位一直处于高水位等一致。

4.4.3 静态与动态相结合

依据贝叶斯估计的原理，对于多项似然函数，其共轭分布族是狄利克雷分布[16]。

在大坝稳定服役阶段，假定其先验分布是β分布，可得下一个样本的贝叶斯估计。当样本量很少时依赖于专家经验，当随着样本数据的增多，失效概率依赖于样本。图7反映失效概率的动态变化过程，当证据(实测数据)增多且没有风险因子加入时，失效概率趋于稳定。4个指标的失效概率分别收敛于0.006、0.007、0.003、0.003。

图7 失效概率变化曲线Fig.7 Change curves of failure probability

5 结 论

本文以贝叶斯网络为主要框架，提出了一种结合专家主观经验和客观实测数据的大坝性态评估方法。主要得出的结论如下：

(1) 根据模糊综合评价法可以量化专家经验，防止数据出现过拟合现象；采用熵权和距离权给予不同权重，使条件概率推理更具可靠性。二者结合可以给出既满足经验又考虑实测数据的失效概率。

(2)利用贝叶斯网络可以有效地厘清影响因素之间的关系，依据失效概率表达的服役性态可以明确失效程度。二者结合有助于工作人员清晰地评估性态，采取合理措施规避风险。

(3)根据模型的结果，可以推断出案例中的混凝土坝综合评级为3级(中等风险)。其中变形指标的失效概率(3级)最大，应该加大变形监测，采取措施控制变形的持续开展，这与实际安全鉴定结论基本一致。

本文采用的方法只是提供一种融合多元信息的评估模式，实际运行过程中失效概率的确定远不止如此，涉及大坝的内部机理和外在影响，需要进一步探究。