求解二维装箱问题的强化学习启发式算法*
2021-02-25阳名钢陈梦烦杨双远张德富
阳名钢,陈梦烦,杨双远,张德富
(厦门大学 信息学院,福建 厦门 361005)
二维带形装箱问题是指将一组矩形小物品装入一个具有给定宽度、但是高度无限的矩形箱子中,这些矩形只能按照固定方向放置,不能相互重叠,且必须完全装入箱子中.问题的目标是使得使用的高度尽可能的低.
二维装箱问题是经典的组合优化问题,在各行各业中都有着非常广泛的应用.如在石材切割中,物品是小块的石材,箱子则对应待切割的完整石板,目标是使石材的利用率更高.由于装箱问题广泛地存在于各个领域,高效的求解算法有助于公司节省材料和减少资源浪费,提高生产和工作效率,帮助更合理利用有限的资源.多年来,二维带形装箱问题(2DSPP)被众多国内外学者研究以获得更快更优的解决方案.与其他组合优化问题一样,2DSPP 可通过精确算法、近似算法(启发式和元启发式)或者混合算法等来求解[1].
精确算法可以找到问题的最佳解决方案,但在较大的问题实例上通常需要花费大量的时间.Hifi[2]基于分支定界过程提出了一种精确算法用于解决带状切割和包装问题,该算法在可接受的执行时间内解决一些中小规模问题实例.Martello 等人[3]提出了一种新的松弛方法,该方法可产生良好的下界,基于此下界构造出较好的启发式算法.Kenmochi 等人[4]设计了一个基于分支规则和边界操作的分支定界算法.Côté 等人[5]提出了一种基于Bender 分解的精确算法,该方法可以在有限的计算时间内解决中小规模的基准实例.大多数精确算法都是基于分支定界策略或者混合整数线性规划,但是因为装箱问题的复杂性,当问题实例增大的时候,不可避免地导致计算量的指数级增长,耗时增加.故大部分精确算法仅在小规模的数据集上表现良好,对于解决大规模的问题实例,更多的研究重点则倾向于使用近似算法来解决.
启发式算法虽然无法保证获得的解是最优的,但是它能在合理的时间范围内给出良好的解.启发式被认为是解决大规模组合优化问题的有效解决方案,因此在装箱领域中十分流行.大多数启发式算法都包含构造性过程,即每次将一块添加到现有的部分解决方案中.1980 年,Baker 等人[6]为了构造合理的装填顺序,就提出了左下(bottom-left,简称BL)启发式算法.该算法每次取出列表中的第1 个矩形,放入容器最左最低的可用空间.Chazelle等人[7]对BL 算法进行了改进,提出了左下填充算法(BLF).算法首先确定即将被放入的矩形合适的所有位置,然后选择其中最低位置.Huang 和Liu[8]提出了基于欧氏距离的确定性启发式求解算法.Burke 等人[9]提出了最佳填充算法(BF),该算法会动态地在列表中搜索放入可用空间的最佳候选矩形.Leung 等人[10]提出了适合度策略,该策略用于决定哪个矩形要填充到指定位置.
元启发式算法常见的有模拟退火(SA)、遗传算法(GA)、蚁群算法(AC)和禁忌搜索算法(TS)等,大多数研究者会结合构造性启发式和元启发式算法来解决二维带形装箱问题.Jakobs[11]在提出的遗传算法中,使用一个特定的交叉算子和变异算子来交换某些元素的位置,并使用BL 算法解码解决方案.Hopper 和Turton[12]混合BL 方法与3 种元启发算法(遗传算法(GA)、模拟退火算法(SA)、朴素演化(NE))和局部搜索启发式算法.其他作者[13,14]也提出了多种结合遗传算法的方法来解决2DSPP.He 等人[15]提出了动态归约算法求解面积最小的装箱问题.Wei 等人[16]开发了一种基于配置文件的构造启发式算法的禁忌搜索算法.Alvarez-Valdés[17]提出了一种针对带状包装问题的贪婪随机自适应搜索程序(GRASP).Zhang 等人[18]提出了基于随机局部搜索的二分搜索启发式算法.Leung 等人[19]提出了两阶段智能搜索算法(ISA),该算法基于简单的评分规则选择矩形放入,该评分策略中设置了5 个分值(0~4).在简单随机算法(SRA)[20]中使用了具有8 个分值的评分规则,并引入了最小浪费优先策略.Chen 等人[21]提出了新的算法框架CIBA,提出了角增量的概念,只包含了4 个评分值,用于在选择矩形的时候评价矩形.Chen 等人[22]基于评分规则以及角增量的基础上,再结合分层搜索的思想,提出了一种混合启发式算法.这些不同的评分规则设计的大致思路都是想实现更平坦平滑的布局,以此来减少空间的浪费.值得注意的是: Chen 等人[22]研究了解的不同初始化策略,如贪心策略,最后在6 种贪心策略中选择最好的初始序列,取得了不错的效果.
深度学习算法在分类、回归任务和图像识别等方面取得了非凡的成功,但是将机器学习用于组合优化问题的求解,进展仍然缓慢.1985 年,就有学者在组合优化问题中使用神经网络用于优化决策,该论文使用Hopfield 网络解决小规模的旅行商问题(TSP)[23].组合优化问题大部分都是序列的决策问题,例如旅行商问题就是求解访问城市顺序的问题.Vinyals 等人[24]设计了一种非常适合用于求解组合优化问题的神经网络,指针网络(PointerNetwork,Ptr-Net),该模型使用注意力机制[25]作为指针来选择输入序列中的某一个元素输出.作者将该模型应用在解决旅行商问题上.Bello 等人[26]采用了Actor-Critic 算法来训练Ptr-Net 并在多达100 个节点的TSP问题上获得最佳结果.受到Bello 等人[26]工作的启发,Nazari 等人[27]提出了一个强化学习解决车辆路径问题的端到端框架,该框架中简化了指针网络,采用Actor-Critic 算法训练模型.Kool 等人[28]提出了基于注意力机制的模型,并用该模型求解了各类型的TSP 和VRP,以及其他组合优化问题.Hu 等人[29]提出了新型的3D 装箱问题,受到深度强化学习(DRL),尤其是指针网络在组合优化问题上的应用启发,使用DRL 方法来优化要装填的物品的顺序,结合启发式算法,将网络的输出序列转换成解决方案,用于计算奖励信号,实验结果优于之前精心设计的启发式算法.
可以看到,强化学习在组合优化问题上的研究和应用处于初步研究阶段,性能还不是很好,但是新的思路不断涌出,研究人员也都在尝试能设计更好的模型来解决组合优化问题.目前,强化学习框架的研究大多只在小规模的数据集上获得较为良好的解,如果问题规模增大,信息量爆炸,网络存储能力有限,可能无法获得理想的解.
本文研究了如何利用强化学习来生成一个好的初始解,最终提出了强化学习启发式算法,计算结果表明,提出的方法超过了当前最优秀的算法.最后,也研究了不同初始化策略的影响.
1 启发式算法
由于强化学习需要奖励机制,本文利用构造性算法获得的高度作为奖励机制.矩形的选择方法是整个构造性启发式算法的关键.本文采用文献[22]提出的矩形选择策略——δ评分规则.算法1.1 详细地介绍了基于δ评分规则和红黑树的构造性启发式算法的过程.算法中将迭代放置所有的矩形,在每次选择一个放置空间时,会先判断放置空间是否可用,否则会进行cave smooth 操作,将不可使用的空间合并到y坐标差异较小的相邻cave.详细的构造性启发式算法的介绍见文献[22].
算法1.1.构造性启发式算法.

文献[22]提出的混合启发式算法HHA 取得了不错的结果,但是需要一个好的初始解.本文用强化学习帮助HHA 找到一个更好的初始解.在此给出 HHA 的算法流程,见算法 1.2.其中涉及的函数如构造性算法ConstructiveHeuristic、分层搜索HierachicalSearch 等,见文献[22].
算法1.2.HHA 框架.


2 强化学习启发式算法
2.1 强化学习求解框架
启发式算法通常会存在冷启动的问题,每次运行算法都需要重新开始缓慢的爬山搜索来寻找最优解,无论算法运行过多少次,并不能对后续的运行和搜索产生任何帮助.传统的启发式算法不存在学习或者保存原先经验的能力,而强化学习则可以做到.强化学习是机器学习的一个重要分支,它的算法框架如图1 所示:Agent 是智能体,它会根据所接收的环境状态(state)采取相应的动作(action),环境会根据采取动作给予Agent 不同的反馈(reward);然后,Agent 根据反馈的情况调整和修正自己的行为.Agent 会反复地与环境互动进行探索和学习,目的是使获得的奖励最大.因此,我们考虑使用强化学习的方法,通过训练模型来学习装箱经验,为启发式算法寻找一个较优的初始序列,从而优化冷启动的问题.那么这就需要一个网络模型,能够学习根据输入的物品序列输出一个初始装箱序列.
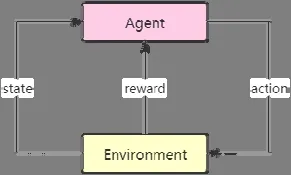
Fig.1 Reinforcement learning graph图1 强化学习示意图
指针网络非常适合解决输出序列强依赖输入序列的问题.而二维装箱问题也可以看成是序列到序列的问题,它的装箱序列完全来自输入的物品,因此可以利用指针网络来学习输出一个合适的装箱初始序列.对于训练好的网络模型,其优势在于当输入全新的数据时,模型可以根据学习到的经验给出一个较理想的初始序列,好的初始序列不仅可以加快启发式搜索算法的响应速度,还可以节省爬山消耗的时间,提高算法性能.
2DSPP 主要有两个决策变量:(1) 矩形物品放入箱子的顺序;(2) 物品摆放的位置.算法1.1 可以用于解决输入物品的序列如何放置物品的问题,而提出的强化学习方法用于优化物品的放入顺序.
本文提出的框架是使用强化学习训练好的模型为启发式方法提供初始的装箱序列,改善冷启动问题.具体的框架图2 所示.强化学习方法是一种自我学习驱动的过程,该过程仅依赖输出序列所计算获得的奖励值来训练网络.网络模型(即图 2 中的 Net)采用简化版的指针网络输出一个初始的装箱序列,然后调用ConstructiveHeuristic(即算法1.1)计算该装箱序列所获得的解,将该解获得的高度值作为奖励信号来验证网络的可行性,根据奖励值不断的调整网络,使网络能以最大的概率输出较好的装箱序列.训练好的模型将为HHA提供初始序列,整体的算法本文称为强化学习启发式算法(reinforcement learning heuristic algorithm,简称RLHA),详细的算法流程见算法2.1.
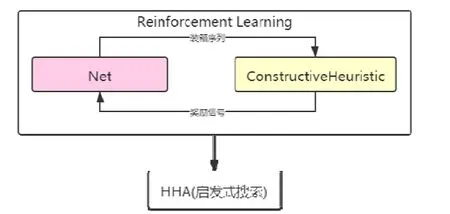
Fig.2 Reinforcement learning heuristic algorithm framework图2 强化学习启发式算法框架
算法2.1.强化学习启发式算法.

2.2 网络模型
网络模型使用的是简化版的指针网络,该模型结构与Nazari 等人[27]使用的结构一致,其框架考虑了静态和动态的元素.针对二维装箱问题,我们仅考虑了静态元素,因为装箱问题与VRP 不同,2DSPP 不存在动态的元素,比如VRP 的配送点除了坐标,还有配送点的货物量,这个值是会动态改变的.模型由循环神经网络(GRU)和注意力机制组成,每一步把输入元素的嵌入(embedding)直接作为解码器的输入,解码器的输出会传递给注意力机制,获得输出的概率分布.Nazari 等人[27]认为: 循环神经网络编码器增加了额外的复杂性,因为只有当输入需要传递顺序信息的时候才需要循环神经网络.比如文本翻译,需要知道词的先后顺序才能准确翻译.但是在组合优化中输入集并没有顺序之说,任何随机排列都包含与原始输入相同的信息.因此在简化版指针网络中,忽略了编码器,直接使用了嵌入层(embedding layer)代替编码器.本文同样使用了简化版指针网络,因为通过这种修改减少了计算的复杂性,提高了性能.
本文的网络模型如图3 所示,该模型由两个部分组成.首先,嵌入层(embedding)对输入的序列嵌入映射成D维的向量空间,使用的是一维卷积层对输入进行嵌入;右边是解码器保存序列的信息,它将利用注意力机制将解码器的隐藏状态和嵌入的输入指向一个输入元素.

Fig.3 Network model图3 网络模型示意图
设输入集为X={xi,i=1,…,N},其中,xi=(wi,hi)是个元组,表示每个物品的宽度和高度.Xt表示在t时刻所有输入的状态集合.从任意的输入X0开始,使用指针y0指向该输入,每一次解码时刻t,yt+1将指向当前可用的输入Xt中的一个,并将其作为下一个解码器的输入.如此重复,直到所有的序列都被输出.整个过程将产生一个装箱序列,高度同输入相等为N,Y={yt,t=1,…,N}.模型是要找到随机策略π,使得在满足问题约束的同时最小化损失目标的方式生成序列Y.我们要做的就是:使得π尽量的接近最优解π′,尽量以百分百的概率生成最优解.使用概率链规则分解生成序列Y的概率P(Y|X0)表示如下:

在解码器的每一步,使用注意力机制生成下一个输入的概率分布.设是嵌入式输入i,ht是解码器在t时刻隐藏层的状态,对齐向量ait表示输入的序列在下一个解码时刻t中的相关程度,公式如下:

这里的对齐模型采用concat 映射,“;”表示拼接两个向量.上下文向量ct计算公式如下:

结合ct和嵌入式输入,然后使用softmax函数归一化结果可得:

2.3 模型训练
2.3.1 Actor-Critic
为了训练网络模型,本文采用强化学习的方法.我们使用基于策略梯度的强化学习来优化网络参数θ.策略梯度的思路是:使奖励越大的动作出现的概率变大,通过反复训练,不断地调整网络参数.本文选择Actor-Critic的方法来训练网络,相比传统的策略梯度下降方法,它有以下优点:(1) Actor-Critic 使用了策略梯度的方法,可以在连续动作或者高维的动作空间中选择适合的动作,采用值函数的方法是做不到的;(2) Actor-Critic 相比单纯的策略梯度的方法,它结合Q-learning 的做法,使得Actor-Critic 可以做到单步更新,比起单纯的策略梯度的回合更新效率更高.
Actor-Critic 是由两个网络Actor(执行者网络)和Critic(评论者网络)组成,如图4 所示.Actor 网络是基于概率选择动作,Critic 网络基于Actor 网络选择的动作评价动作的优劣,Actor 网络根据Critic 网络的评价修改行为的概率.它将值函数和策略梯度两种强化学习算法优点结合,使得算法可以处理连续和离散的问题,还可以进行单步更新.

Fig.4 Actor-Critic network structure图4 Actor-Critic 网络结构

设Actor 网络为π(s),则其网络参数θ的梯度公式表示如下:
其中,ω是Critic 网络V(s)的网络参数,它的网络参数梯度公式如下:

在公式(7)和公式(8)中:N是样本实例,Rn表示第n个样本实例获得的奖励值,表示第n个样本实例所有输入的状态集合,是Critic 网络的输出.Rn是当前获得的奖励值,由启发式算法根据网络输出序列计算获得.是优势函数,它表示在的状态下采取动作的优劣.如果优势函数的结果是正的,则会增加 该动作出现的概率,否则降低概率.
Actor-Critic 的算法流程如算法2.2 所示,我们使用θ和ω分别表示是Actor 和Critic 的网络参数.在第4 行,我们将样本分成N输入网络; 第7 行~第10 行是使用简化的指针网络以及注意力机制获得下一个输出的概率分布,每次选择一个物品,停止的条件是当所有物品都被输出.第11 行计算该输出的奖励值,R(·)是奖励计算函数,也就是算法1.1 计算装箱的高度将作为奖励信号Rn.第12 行、第13 行将计算相应的奖励以及策略梯度.最后,根据计算的梯度更新两个网络.Critic 网络将使用Actor 网络输出的概率分布来计算嵌入式输入的加权和.该网络具有两个隐藏层:第1 层是使用relu 激活函数的稠密层,另一个是具有单个输出的线性层.最后对两个网络进行更新.
算法2.2.Actor-Critic 算法流程.


2.3.2 探索机制
强化学习的探索机制会直接影响采样的性能,本文在模型的训练阶段,会通过根据概率分布按概率进行随机采样下一步作为输出.在测试期间采用的是贪婪的方法,选择概率分布中概率最高的输出.
3 计算结果
为了验证强化学习启发式算法并评估其有效性,本小节将进行一系列实验分析.首先阐述了实验数据的生成方法,然后对实验环境和参数设置进行说明,最后对实验结果进行分析.
3.1 实验数据
由于现有的标准数据集都是较为零散且实例的数量较少,目前缺少较大量的装箱问题的数据集来用于强化学习模型的训练,因此本文采用了Bortfeldt 和Gehring[30]提出的装箱数据生成算法以及Wang 和Valenzela[31]提出的装箱数据生成算法.
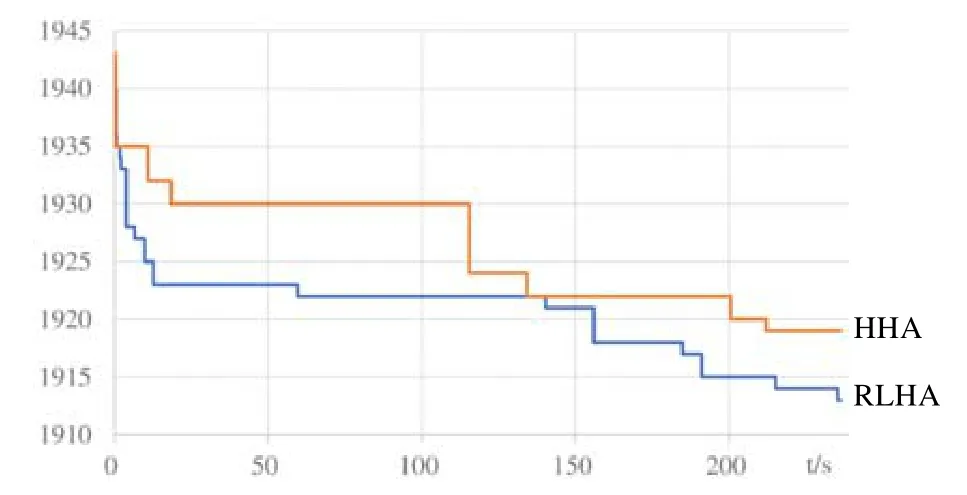
Bortfeldt 和Gehring[30]生成数据的思路是:通过一些参数,控制生成的矩形的数量、大小、宽高比以及面积比等.该算法生成的数据是非零浪费率的,因此我们无法知道生成的数据的最优解.算法3.1 是该算法的流程,该算法需要输入6 个参数:wC表示矩形条的宽度;n表示矩形总个数;nt表示要生成的矩形的种类; Δg和ρg这两个参数是用于计算矩形的最大边长和最小边长;最后,seed是随机种子.γ是异质性比,等于nt/n.首先,算法根据输入的参数计算生成矩形的边长范围[dming,dmaxg],然后根据随机种子初始化随机数生成器.再循环nt次生成nt个类型的矩形rects,矩形长宽的范围介于[dming,dmaxg].最后,循环n次生成n个矩形rect_list,rect_list依照rect_list[i]=rects[i%nt],0≤i 算法3.1.数据生成算法1. Wang 和Valenzela[31]生成数据的算法思路是: 通过将一个大的矩形不断地进行分割,分割成满足一定面积比(γ)和宽高比(ρ)的小矩形.这种思路生成的数据集是属于零浪费类型的,装箱的最优解由输入参数控制.具体的算法流程如算法3.2 所示.该算法输入的参数有4 个:n表示生成小矩形个数,H表示待分割矩形的高度,γ和ρ控制生成矩形的面积比和宽高比.算法一开始根据输入的参数随机选择宽度W,然后在第3 行~第18 行进行n-1次切割,生成n个矩形.首先,随机选择满足面积小于2m/γ的矩形进行切割,m是矩形序列中最大矩形的面积.在第7 行~第13 行,根据不同的条件选择切割方向.第13 行~第18 行根据不同的切割方向,在可切割的范围内随机选择切割点,并把生成的两个新矩形加入列表中. 算法3.2.数据生成算法2. 本文使用算法3.1 和算法3.2 共生成1 000 000 组的数据用于训练模型,共3 种矩形块数:(1) 矩形块数为200生成400 000 组数据;(2) 矩形块数为100 生成300 000 组数据;(3) 矩形块数为50 的块数共生成300 000 组数据.同时生成100 000 组数据集作为测试样本.通过随机种子生成较大的训练数据集,是为了能尽可能地涵盖不同的样本,使得模型能学习到丰富的样本. 强化学习模型主要通过pytorch 实现,实验运行环境如下:Ubuntu 16.04 LST,处理器为Intel Core E5-2620 v4,处理器频率2.10GHz,内存62G,显卡为NVIDIAGeForceRTX2080Ti,显存为11G. 在实验中,我们使用了1 000 000 组的训练数据和100 000 组的测试数据.在实验过程中,每批训练的样本量是128,解码器中GRU 的隐层单元数量为128,输入数据也将被嵌入到128 的向量中.本文使用Xavier[38]初始化方法对Actor 和Critic 网络进行初始化,使用Adam 优化器,学习速率为0.0001,同时,为了防止过拟合的问题,使用了L2 范数对梯度进行裁剪.在解码器中使用了0.1 的dropout,dropout 可以比较有效地缓解过拟合的产生.模型在单个GPU 上训练1 000 个时期. 训练好的模型将为HHA 提供初始解,接下来,我们将把RLHA 和目前优秀的启发式算法GRASP[17],SVC[32],ISA[19],SRA[20],CIBA[21]和HHA[22]算法进行实验对比,验证算法的效果.每个算法将在所有的数据集上运行10次,每个实例的运行时间限制为60s,部分大规模数据集运行时间会超过60s.对比算法的实验结果直接取自原文献(原文献中的参数设置都是原作者通过实验选择的最优参数),以保证算法对比的公平性. 为了验证RLHA 的有效性,我们将训练好的模型框架同当前著名的启发式算法进行对比分析.本节进行对比分析的实验数据一部分来自标准的数据集,为了更合理地说明RLHA 的性能,另一部分是由算法3.1 和算法3.2 生成的数据.由于训练的数据集与强化学习的算法性能还是存在一定关联的,因此另一部分实验分析将在数据生成算法生成的数据上进行,可以更客观的展现算法的性能. (1) 标准数据集的对比分析 我们将在C[12],N[9],NT[33],2SP[17],BWMV[34,35]和Nice&Path[36]这6 个标准数据集上进行实验(见表1),对比7个算法的实验效果,用粗体标出最佳解的数据.之所以没有考虑标准数据集ZDF[37]的原因在于:这个数据集存在大规模的实例,目前强化学习模型在处理大规模的实例时,运行时间会过长.由于计算能力和运行时间的限制,这两个包含大规模问题实例的数据集就不做实验分析. Table 1 Benchmark data表1 标准数据集 从表2 的实验结果可以看出,RLHA 在N 数据集上的表现同HHA 表现一样.N 数据集是一个零浪费率的数据集,我们的算法在大部分实例上都已经取得最优解,因此两个算法在这个数据集上表现并无差别.RLHA 在2SP 数据集上的表现与HHA 获得的结果持平.出现这个情况的原因可能与该数据的特点有关系,该数据矩形个数较少且存在一些比较特殊的实例,需要更精细的策略来改善.我们的启发式设计的规则在这个数据集上的表现可能陷入了瓶颈,因此并没有取得更优的结果.对其余数据集,RLHA 均超过了 HHA,在所有数据集的表现,RLHA 均显著超过了其他5 个算法. RLHA 在C,NT,BWMV,Nice 和Path 上的表现都比HHA 略提升了一些,虽然提升的幅度不大,但是可以看到,强化学习模型的加入的确提升了实验结果.这也可以说明强化学习模型能有效地改进启发式获得解的质量. Table 2 Computational results on benchmark data表2 标准数据集的实验结果 值得注意的是:由于目前现有的针对组合优化问题提出的神经网络模型[26-28]在解决TSP、VRP、装箱等问题时,其数据集规模大部分都是针对少于200 个节点的问题实例.这是由于处理大规模实例的数据集时会导致模型训练的时间过长.由于实验条件等限制,本文训练数据集的矩形块数分别是50,100,200.本文的强化学习模型与解决问题的规模是无关的,也就是说,可以把训练好的模型用于不同规模的数据集上.我们将训练的模型用于处理矩形块数为1000~5000 的数据集Nice 和Path,从表2 中Nice 和Path 的实验结果可以看出:虽然模型并没有训练过矩形块数大于200 块的数据集,但是训练之后的模型在中小规模的数据集上的表现也有一定的提升.这也说明模型可以根据保存的装箱经验,为启发式算法提供一个有效的初始解序列,帮助算法更好地运行,提高算法性能. (2) 生成数据集的对比分析 表3 是生成数据集的明细,分别生成矩形块数为50,100,200 以及1 000 的数据集各100 组,用于对比实验的数据集.由于算法3.1 生成的数据集的最优解不确定,因此这里分别将算法在这4 组数据上运行,将获得的最优解的装箱高度的平均值作为比较指标.表4 为实验的结果,avg_height表示装箱高度的平均值,更优的解将用粗体标出. Table 3 Details on generated data set表3 生成数据集明细 Table 4 Computational results on generated data set表4 生成数据集实验结果 上节实验结果表明,HHA 和RLHA 显著的超过了其他7 个算法.这节只将两个最好的HHA 和RLHA 算法进行对比.表4 是HHA 和RLHA 在4 组数据集上获得的平均装箱高度的数据,从中可以看出:在数据集Test50上,HHA 和RLHA 获得平均装箱高是一样的.这是因为在较小的数据集上,两个算法框架的搜索能力都足够,因此实验表现一样.在数据集Test100,Test200 和Test1000 上,RLHA 的表现均优于HHA 的表现,说明了训练的强化学习模型能使HHA 获得更好的性能. 图5 是Test200 某个实例上分别运行RLHA 和HHA 的结果,两个算法分别运行240 秒,每秒钟输出当前获得最优解的值.图中横坐标是时间(s),纵坐标是最优解的值,也就是装箱的高度.从图中曲线趋势我们可以观察到:RLHA 获得的初始解比HHA 获得的初始解更好,虽然开始优势并不是特别明显,但经过一段时间的运行,RLHA 能较快地朝更好的解方向发展,这也说明输入序列对启发式算法的影响.中间部分RLHA 同HHA 一样,都处在一个较为缓慢的搜索状态.在运行后期,RLHA 获得的装箱高度不断地下降,虽然HHA 也取得了一些不错的进步,但是RLHA 的效果优于HHA.因此也可以看出:RLHA 能较有效地改善启发式冷启动的问题,并能提高算法的搜索性能. RLHA 是使用强化学习获得初始序列,而HHA 是使用6 种排序方法[39](见表5 中的方法1~方法6),并选择最好的序列,表2 和表4 的计算结果表明,RLHA 的性能超过了HHA.为进一步研究初始化方法的影响,我们再增加了一种随机初始序列方法.为测试不同初始化方法的影响效果,我们采用典型的BWMV 数据(该数据包含500个实例).表5 给出了8 种产生初始序列方法的计算结果,从中可以看出:随机初始序列方法效果最差,使用强化学习获得初始序列,效果明显超过其他7 种方法. Table 5 Computational results on different initialize methods for BWMV表5 不同初始化方法计算BWMV 的结果 强化学习启发式算法框架中,我们创新性地使用强化学习的方法来改善启发式算法冷启动问题.强化学习模型仅使用了启发式算法计算的装箱值作为奖励信号,来训练网络,最后输出给定分布中最优的序列.使用简化版的指针网络来输出装箱序列,该网络简化编码器部分的网络,节省了一大部分的计算能力,提高了效率.采用Actor-Critic 算法来训练网络,由于Actor-Critic 可以单步更新,比起单纯的策略梯度的回合更新效率更高.实验部分,本文通过数据生成算法生成了训练模型的数据集.在714 个标准问题实例和400 个生成的问题实例上测试RLHA,实验结果显示,RLHA 获得了比当前著名启发式算法更好的解.这也表明了训练的强化学习模型能为HHA 提供更好的初始的装箱序列,有效地改善冷启动的问题.将来的工作就是在改进框架的基础上对启发式算法进行进一步的改进.同时,将强化学习应用于别的NP 难问题的求解,总结出一般性的求解框架,并进行更多的应用. Fig.5 Comparison of running time图5 同时间运行对比
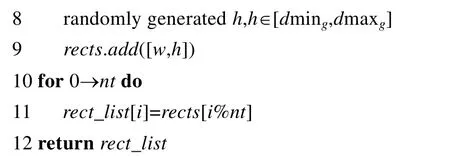

3.2 实验环境和参数设置
3.3 实验结果




3.4 不同初始化方法的影响

4 结 论