双层Boussinesq模型非线性波浪模拟研究

饶永红，刘忠波，梁书秀，李 欣

(1.中国人民解放军91053部队，青岛 266100； 2.大连海事大学 交通运输工程学院，大连 116026； 3.大连理工大学 海岸和近海工程国家重点实验室，大连 116023)

波浪是近岸水域主要的水动力，掌握波浪资料对建筑物结构设计、泥沙运动、海床演变十分重要。作为一种水工构筑物，潜堤常用于促淤保滩，潜堤的存在使局部水深减少，浅水更有利于产生高次谐波，过浅时波浪将发生破碎，损耗大量波能，减小了堤后波高。波浪与潜堤相互作用问题的研究是海岸工程界和学界关注的课题，工程界多关注采用什么样的结构型式更有利于减少堤后波浪，学界多关注如何精准地描述波浪在潜堤上的演变过程。

潜堤上的波浪传播变形是复杂的水动力过程，其涉及波浪反射、变浅效应、反变浅效应甚至波浪破碎等现象。为了研究潜堤上的波浪传播变形特性，众多国内外学者利用理论解析、物理模型试验或数值模型模拟等多种方式开展研究。Beji和Battjes[1]、Luth等[2]、Ohyama等[3]、邹志利等[4]开展了不同的物理模型试验来研究波浪传播变形，试验数据被用来验证各类数值模型。时莹等[5]基于前坡1:15、后坡1:5潜堤的物理模型试验，考察了SWAN 模型对潜堤上波浪演化的模拟能力，发现谱平均周期计算值明显偏小，频谱模拟出现高频高估、低频低估现象，三波非线性项的计算精确度影响了模型在近岸浅水区谱平均周期和频谱的模拟能力，需更多改进。史宝凯等[6]基于δ-SPH方法，通过在控制方程中引入介质阻力项，建立波浪与多孔潜堤相互作用的数值波浪水槽，数值模拟与物理模型试验结果较好。基于典型的势流理论，Boussinesq方程是一种常用的波浪数值模拟工具，然而不同的Boussinesq方程模型，存在多种表达形式，理论、性能存在明显差异，所以，模拟波浪水动力的精度也不同(Madsen和Fuhrman[7]；Brocchini[8]；Kirby[9]；张尧等[10]；琚海军等[11]；孙家文等[12])。波浪演化研究的重点为波面位移和波浪速度，前者用于计算波高、平均水位(增减水)和非线性波浪参数，后者是计算水工建筑物波浪力荷载的依据。精确模拟波面演变的全过程，需要数值模型具有优良的色散性能(相位)、非线性(描述和差频和高次谐波波幅)和变浅性能(变浅波幅)，而精确模拟波浪速度场则要求模型具有良好的速度垂向分布特征。Liu等[13]给出的多层Boussinesq方程，在色散性、非线性以及速度分布特征等方面理论适用水深得到较大的拓展，该模型已被应用到滑坡兴波、浅水非线性长波、聚焦波、深水双色波、流函数强非线性波浪和陡坡潜堤上的波浪传播变形等[14-17]。

然而，多数Boussinesq方程模型以波面位移为主要研究内容，对波浪水平速度和垂向速度未进行深入研究，在研究潜堤上波浪传播问题时，也仅以相关试验来考察模型的适用性。Liu等的多层Boussinesq方程[16]，理论上具有良好的线性和非线性性能，但研究仅限于用一些理想情况或以试验为依据讨论方程的适用性。本文以Liu等的双层Boussinesq方程模型[13]为研究对象，考察模拟1:4坡度潜堤上非破碎波浪演变的能力；为验证模型精度，开展了相应的物理模型试验。研究内容包括：(1)该模型对潜堤上强非线性波浪波面演化的模拟能力；(2)方程能否精确模拟波浪速度场。

1 数值模型

1.1 控制方程

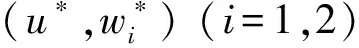
(1)在自由水面处，满足以下运动学和动力学边界条件

(1)

(2)

(2)自由面处与静止水位处的速度关系表达式为

(3)

(4)

(3)静止水位处的速度与上层计算速度之间满足关系式

(5)

(6)

(4)在连接上下两层水体处，满足速度相等条件，即

(7)

(8)

(5)在水底处，海底为不可穿透的运动学边界条件，即

(9)

(10)

式中：下标x表示变量对空间x求导；g为重力加速度；h是静止水平面下的水深；色散系数α1和α2分别取值为0.172和0.328。

1.2 任一水深处的水平速度和垂向速度

(11)

(12)

(13)

(14)

(15)

(16)

式中：zα1=-α1h；zα2=-(2α1+α2)h

表达式(11)、(12)至(15)、(16)给出了水平和垂向速度的表达式。当水深z位于区间[-h, -2α1h]时，采用表达式(11)、(12)进行求解；当z位于区间[-2α1h,0]，采用(13)、(14)求解；当波面高于静止水位z=0时，采用(15)、(16)计算速度。

1.3 数值模型的求解

本文模型最高空间导数是2，比开源程序FUNWAVE对应方程的空间导数少1[18]。为此，本文模型在时间格式上采用与FUNWAVE源程序一样的混合4阶Adams-Bashforth-Moulton(ABM)格式。在预报阶段，先利用显示3阶Adams-Bashforth格式计算方程(1)与(2)，可获得水面位移和自由水面处水平速度的预报值；进一步依次求解方程(3)、(5)和(7)可得3个水平速度的预报值，进而求解方程(9)、(8)、(6)和(4)得到4个垂向速度的预报值。在校正阶段，采用4阶Adams-Moulton时间差分格式求解方程(1)和(2)，可求得水面位移和自由表面处水平速度的校正值，而其他速度校正值的求解过程类似预报阶段。当所有变量的校正值与预报值的误差控制在0.000 1内，当前计算结束，否则重新赋值给各个变量后继续进行迭代求解。

图1 方程的无因次相速度Fig.1 Non-dimensional phase celerity of the model

为了避免地形反射波浪引起造波板的二次反射，在数值模型中，引入了Hsiao等[19]的内波造波技术，且在计算域两端边界设置海绵层来吸收波浪[18]。

1.4 模型的理论性能

为了展示方程相速度与速度场的模拟精度，图1给出方程的无因次相速度，图2给出kh=0.5、1、3和6时方程解析速度场与Stokes线性波解析解的比较，对应的沿水深积分速度误差见图3。其他非线性特征的计算精度可参阅Liu等的文献[16]。

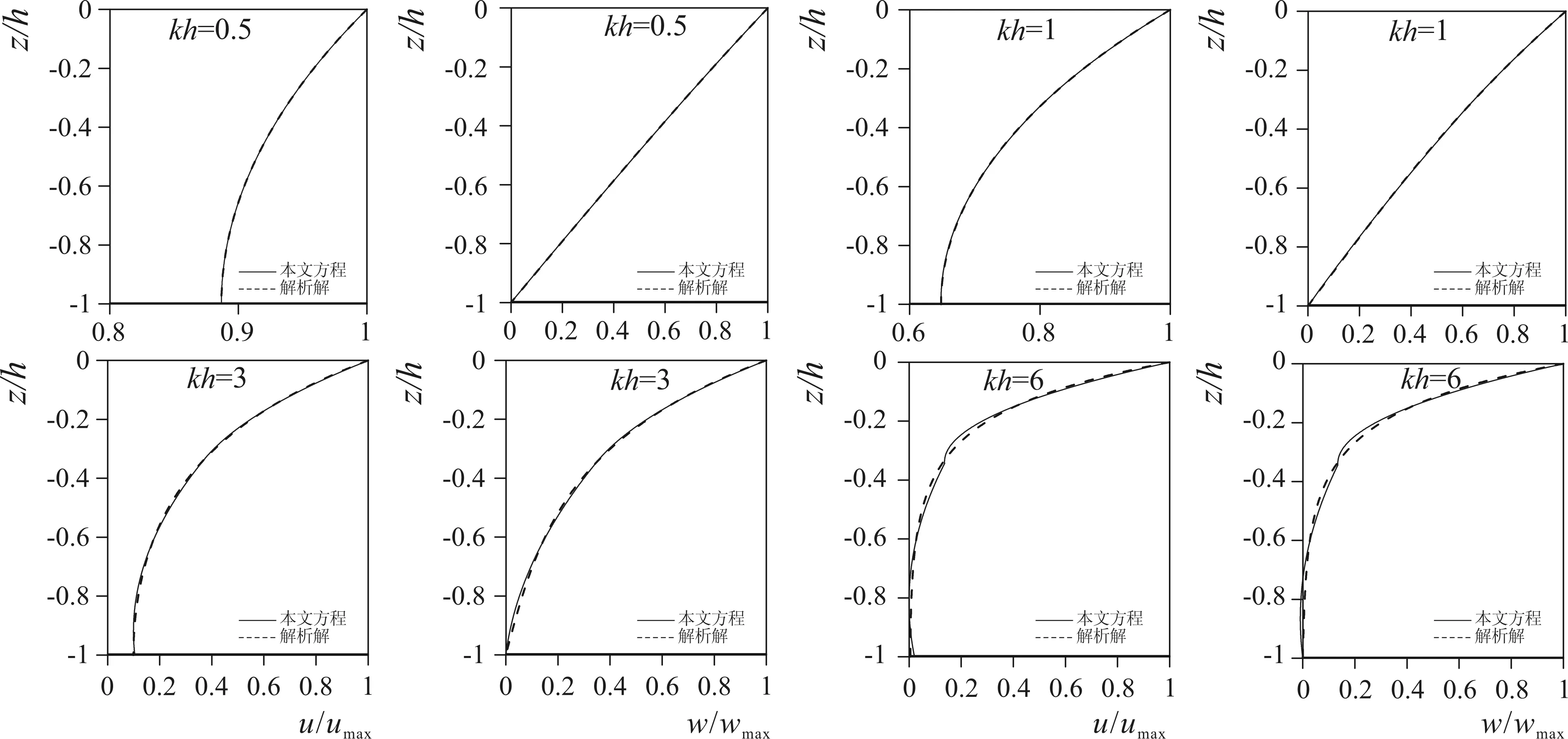
图2 方程的速度分布Fig.2 Velocity profile of the model

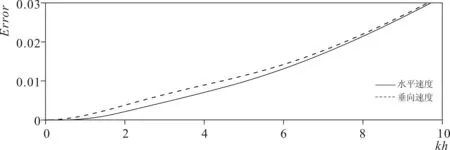
图3 沿水深积分的速度误差Fig.3 Error of the integrated velocity along vertical water depth

表1 波浪要素Tab.1 Wave parameters

2 物理模型简介

物理模型试验在长50 m、宽1.2 m、深1.2 m的波浪水槽中进行，图4为模型布置示意图。试验采用规则波，研究迎浪面和背浪面坡度均为1:4潜堤上的波浪传播变形。水槽水深h为0.5 m，潜堤上方水深h1为0.15 m，潜堤前趾距离造波板15 m。浪高仪设置在距离造波板x=12 m、15.7 m、16.7 m、18.1 m、19.1 m、20.1 m、21.1 m、22.1 m、23.1 m、24.1 m和 25.1 m处。试验中采用超声多普勒流速仪(ADV)测量瞬时流速，垂向方向上布设在静止水位下0.06 m处，水平位置至造波板的距离依次为x=17.4 m、19.1 m和20.232 m。波面位移采样间隔0.017～0.024 s，波浪速度的采样间隔为0.025 s，设置约采集10个波的样本长度。试验中，通过多次重复不同波高(以0.005 m为间隔)入射条件，观察潜堤上波浪是否会发生破碎，从而确定出非破碎强非线性波浪工况，具体见表1，表中k=2π/L，L为波长，A为波幅。

图4 试验布置示意图(单位：m)Fig.4 Sketch of the experimental layout

3 结果比较和讨论

数值模拟中，整个计算长度为60 m，采用0.01 s的时间步长和0.03 m的空间步长。内部造波的中心线设在x=10 m处，对应于试验造波机的0点位置，模拟中前后边界处均设置9 m长海绵边界层吸收波浪。

3.1 波面位移和谐波幅值

以x=12 m处测得的波面位移作为表1入射条件的校核标准，数值模拟中的波浪要素与表1给定的目标值一致。波面位移计算值与试验结果的对比见图5、图6和图7，两者符合程度高。观察其中x=15.7 m和x=16.7 m处的波面位移过程可知，规则波在潜堤前坡上传播时，波浪以锁相波形态存在；而在平坡段(潜堤上方)常水深传播时，浅水容易释放出更多高次谐波，它们在潜堤后坡(x=19.1 m)由于水深增加变为自由波，并以各自相速度传播，因此，坡后出现更为复杂的波浪形态。此外，伴随波浪周期的增大，潜堤上方无因次水深减小，更容易激发出更多的高次谐波，图7中x=18.1 m处出现明显的三次峰就是佐证。

图5 波面时间历程对比 (T=1.4 s, H=0.055 m)Fig.5 Comparisons of the computed surface elevation and the experimental data (T=1.4 s, H=0.055 m)

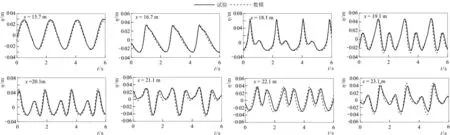
图6 波面时间历程对比 (T=1.8 s, H=0.05 m)Fig.6 Comparisons of the computed surface elevation and the experimental data (T=1.8 s, H=0.05 m)

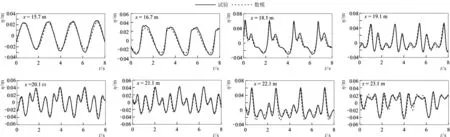
图7 波面时间历程对比 (T=2.2 s, H=0.045 m)Fig.7 Comparisons of the computed surface elevation and the experimental data (T=2.2 s, H=0.045 m)

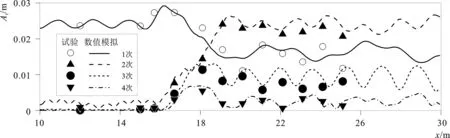
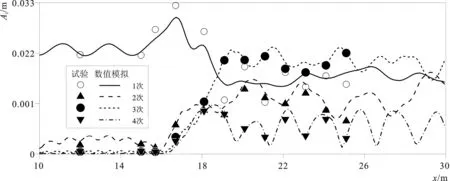
对三组工况的波面位移进行傅里叶分析，得到各次谐波幅值见图8、图9和图10。由图可见，整体上和试验结果吻合良好，且随着波浪周期逐渐增大，高次谐波的幅值快速增加。在潜堤后方(x≥19.1 m)，工况1幅值大小顺序是基频、2倍频、3倍频和4倍频；工况2幅值大小顺序是2倍频、基频、3倍频和4倍频；而工况3幅值大小顺序是3倍频、基频、2倍频和4倍频。进一步统计潜堤后方(x≥19.1 m)7个测点处的各次谐波幅值，并取各点平均值，结果显示，周期1.4 s工况中2倍、3倍和4倍频谐波的幅值平均值依次为基频的0.74、0.11和0.08倍，周期1.8 s工况中该倍数依次为1.50、0.49和0.13，周期2.2 s工况中该倍数依次为0.71、1.31和0.38。其中，工况3的波浪周期和波长最大。堤上相对水深最浅，说明浅水更有利于波-波能量由低频向高频传递，导致堤后3次谐波幅值最大。

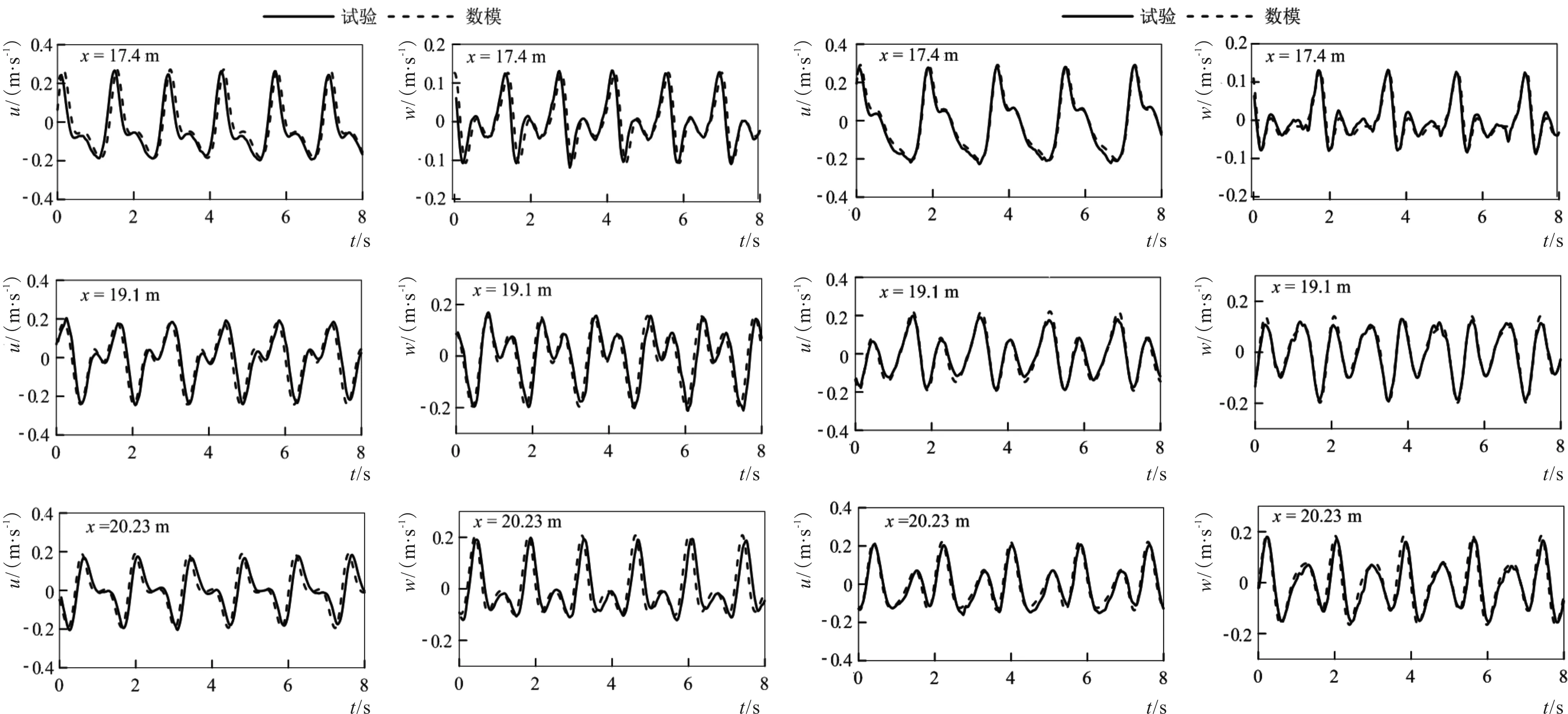
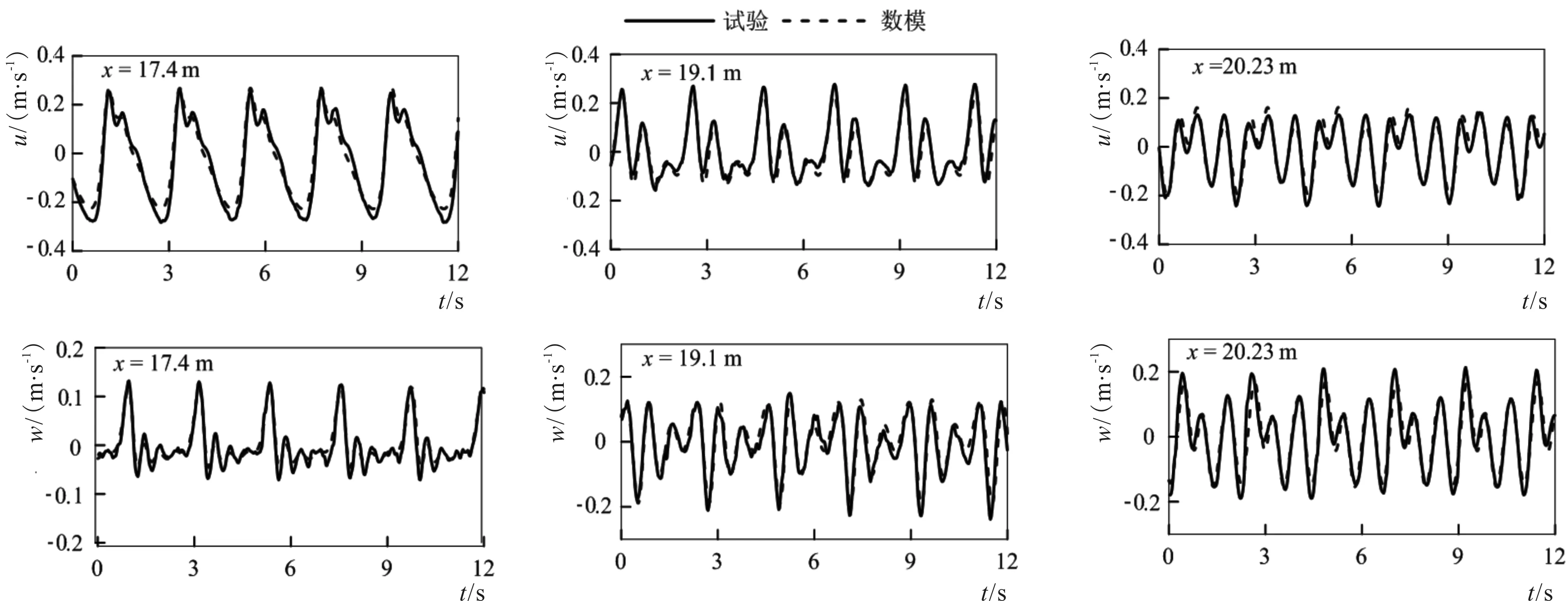
图13 计算流速与试验结果的比较 (T=2.2 s, H=0.045 m)Fig.13 Comparisons of computed velocity and the experimental data(T=2.2 s, H=0.045 m)

3.2 波浪速度

物理模型试验测量了波浪水平速度和垂向速度过程，利用三点光滑(中间值权重0.5，相邻点权重为0.25)进行滤波处理。将计算波浪流速与滤波后试验数据进行比较，详见图11～图13。由图可见，无论是水平速度还是垂向速度，两者流速过程的相位和峰谷值均吻合良好。

3.3 波浪非线性特征分析

对表1的三组工况，采用数值模型计算了最大波峰面高度(ηmax)、最大波高(Hmax)、波长(L1，L2，L3)和最大波峰处的水平速度(uη)。这里L1为浅水线性波长，用Stokes线性波色散关系求解得到；L2为浅水非线性波长，用数值模拟结果分析得到；L3为与流函数波浪对应的波长，分别将1.4 s、1.8 s和2.2 s周期对应的Hmax输入流函数波浪波长数值逼近程序计算得到。计算结果见表2。表中，Hmax/h1为浅水非线性参数，U=HmaxL2/h13为厄塞尔数。由表可见，在潜堤上的平坡浅水水域，波高与水深比在0.539～0.599范围内，属于强非线性波浪，厄塞尔数在68.46～229.79，当每组工况的特征参数超过表2所列临界值之后，波浪将发生破碎。

表2 波浪特征和非线性参数临界值Tab.2 Computed results of wave features and wave nonlinear parameters

4 结论

本文针对双层高阶Boussinesq方程，建立了基于预报-校正-迭代的有限差分数值模型。利用数值模型，模拟了迎浪面和背浪面坡度均为1:4潜堤上强非线性波浪的传播变形，给出了不同位置点的波面位移和速度(传播方向上的水平速度和垂向速度)时间历程。为探究模型的模拟能力，开展了相应的波浪物理模型试验，并确定了强非线性波浪工况。通过以上研究，主要结论如下：

(1)在潜堤上浅水区域，波高与水深之比在0.539～0.599，属于强非线性波浪。本文试验工况的厄塞尔数在68.46～229.79。

(2)针对不同周期的强非线性波浪工况，双层Boussinesq方程模型计算了堤前、堤顶和堤后的波面位移、水平速度、垂向速度，与试验结果吻合程度较高，充分展现了数值模型良好的非线性波浪模拟能力。

(3)随着波浪周期逐渐增大，高次谐波的幅值增加较快，在堤后超过了基频波的波幅，尤其是周期2.2 s工况，3倍频谐波幅值最大，超过了基频和2倍频，这充分说明了浅水更有利于高次谐波的产生。