忆阻基本性质模拟仿真研究
2021-02-25何都益
许 黎,何都益,蒋 强,黄 果
(乐山师范学院 a.电子与材料工程学院;b.图书馆、档案馆;c.人工智能学院,四川 乐山 614000)
0 引言
2008年,惠普实验室Dmitri B.Strukov[1]领导的研究小组在Nature上发表论文“The missing memristor found”,为忆阻的真实性提供了现实依据。论文一经发表,在全世界范围内引起了轰动,忆阻吸引了大量科研人员的关注,掀起了一股研究忆阻的热潮。2010 年,Sung Hyun.Jo[2]等人提出,忆阻器的行为机制与人脑的神经突触很相似,具有高连通性和高密度、高效的计算功能,通过电压的变化可改变忆阻器的阻值,记录现状信息。外界电压消失再恢复后忆阻可直接回到记忆状态,有类人脑功能。因此可运用于人脑传感系统,来收集和传导神经系统的信息。美国南卡罗来纳州大学的科学家Yuriy V.Pershin[3]利用忆阻器构造出了简单神经网络。忆阻器的集成微单元可用来模拟突触,使系统中的每个设备都能和其他设备交互。忆阻具有高速度和高密度的特点,它可将电子器件的功能浓缩到纳米级的微小空间,构成的交叉矩阵也可以以极高的密度作为一个功能独立的单元组织起来,因此可能被用于CPLD 及FPGA的设计中。与以往的存储器相比,忆阻有几个优点:非易失性、可扩展性良好以及有效的无泄漏电流。2012 年,段书凯、胡小方[4]等人基于忆阻的这个特点,提出了混合纳米CMOS 技术,采用忆阻替代RS 触发器实现了10-9米级别兼容现代计算机系统的二进制存储器。Massimiliano Di.Ventra[5]在忆阻器非线性的特性的基础上提出了忆容和忆感的概念。之后Dalibor Biolek[6]等人设计出忆容器和忆感器的SPICE 模型,并提出这些忆阻器衍生器件可应用到机器学习、自发行为等方面的研究。Mineo Kaneko[7]等人应用忆阻器设计出低功耗的数字可编程延时元件。Sangyun Shin[8]等人通过控制脉冲参数控制通过忆阻器的磁通量,从而控制忆阻阻值,即通过脉冲编码忆阻器。这种方法可用于设计可编程增益放大器,通过脉冲变化来改变磁通量从而产生增益效果。忆阻的电阻具有可变性质,故可以用于可编程电阻方面。忆阻器在图像处理、信号处理、算术运算和模式识别等方面也有着巨大的应用潜力。因此忆阻的记忆特性将对生物工程学、通讯工程、计算机科学、神经网络、电子工程等产生极其深远的影响。由此可见,忆阻作为遗失的第四类元件,与其他三类基本元件一样,有着极其远大的应用前景,忆阻的发现和最终的应用将会大大改变我们的生活。对忆阻的研究也极为迫切和重要。
致力于忆阻研究的学者正在持续壮大,国外对忆阻的研究相对较多,日趋成熟;但目前为止,国内研究忆阻的学者却为数不多,有关忆阻的资料也很少,理论仍不系统、不完善。本文参考大量外文文献,首先对忆阻的定义、分类以及性质进行归纳综述,并对忆阻的性质利用MATLAB 进行模拟仿真重现;再对近年来学者提出的诸多忆阻模型进行归纳,将忆阻划分为三种理论模型,并对不同模型进行研究,模拟仿真其性质。
1 忆阻的定义及性质
众所周知,电路系统中有四个基本禀赋变量,见图1。
如图1 所示,电路的四个基本变量为电压v(t)、电流i(t)、磁通φ(t) 和电荷q(t),将{v,i,q,φ}称为电路的基本禀赋变量,这四个基本禀赋变量有六种组合:{(v,φ),(v,i,),(q,v),(i,q),(φ,i),(φ,q)};其中组合(v,φ),(i,q) 之间的关系为[1,9-10]:
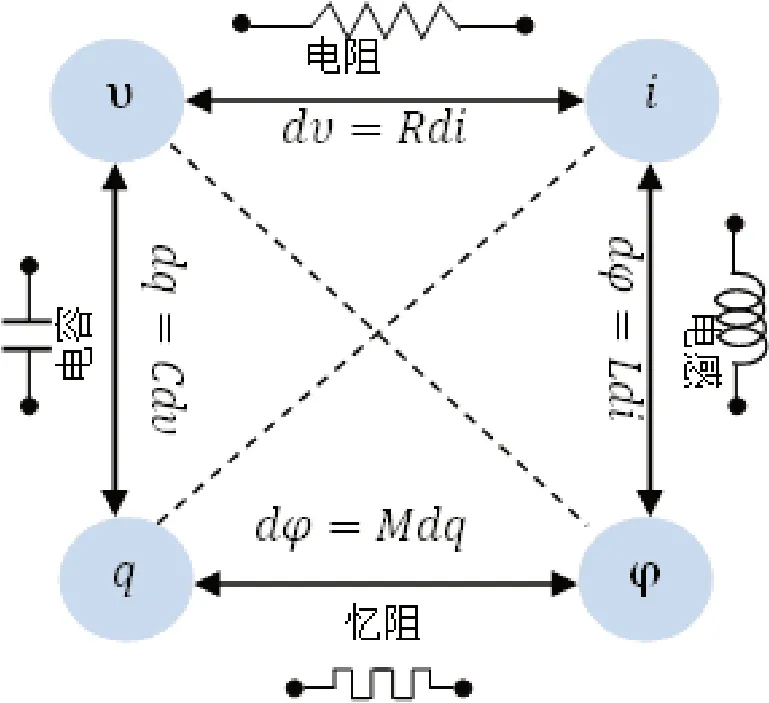
图1 四种基本电路元件及其禀赋关系

它们之间是一种非代数关系,在图中以斜虚线表示。另外三种组合为:(q,v),(v,i,),(φ,i) ;为严格的代数关系,对应了电路的三种经典基本元件——电阻R、电容C 和电感L:

在图中用三条粗黑直线表示。
最后还剩下一对变量对(φ,q),1971 蔡少棠从逻辑相容性、公理完备性和形式对称性等多方面考虑,提出它们之间应存在如下禀赋关系,即

从而得到了一个完整的“基本电路元件四边形”。这种禀赋关系也引入了第四个基本电路元件——忆阻,它是一种具有记忆功能的非线性电阻元件,用符号M 表示:


W 为忆阻的忆导。
忆阻分为两种类型:荷控型忆阻和磁控型忆阻[10]。当M(φ,q) 为电荷的单值函数时,忆阻为电荷控制型忆阻,简称荷控型忆阻;当M(φ,q) 为磁通的单值函数时,为磁通控制型忆阻,简称磁控型忆阻。它们的特征曲线如图2 所示:

图2 忆阻特性曲线
图2(a)的斜率为磁通量随电荷的改变率,即

为忆阻,因此M(q) 为q(t) 的非线性函数。忆阻具有与电阻一样的量纲,单位为:欧姆(Ω) 。
图2(b)的斜率为电荷随磁通量的改变率,即

为忆导。忆导具有与电导一样的量纲,单位为:西门子(S)。
2 忆阻的性质及模拟仿真
判断一个器件是否为忆阻,基本标准是看这个器件是否满足如下三个本质特征[11]:
a)当忆阻被一个双极性周期信号驱动时,其V-I 图为一条在原点紧缩的磁滞回线,且周期性响应;
b)磁滞旁瓣面积从临界频率开始,随着激励频率的增加而减少;
c)当激励频率趋近于无限大时,磁滞回线收缩为一个单值函数。
为验证忆阻的本质特征,构建一荷控忆阻为:M=aq(t)+b,a,b为常量,q(t)为流经忆阻的电荷,是时间的函数,取决于流经忆阻的电流;选用驱动信号为正弦电流:I=Imaxsin(ωt),其中Imax为电压振幅,ω为角频率。令a=-60,b=160,Imax=0.1A,ω=2π,利用Matlab 模拟得到该忆阻V-I图,如图3 所示:从图3 可以看出,V-I 图为一条在原点紧缩的磁滞回线,且周期响应。
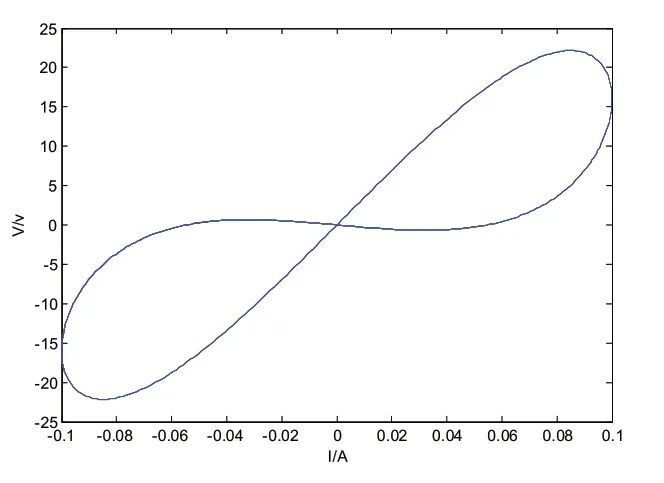
图3 忆阻V-I 图
改变驱动电流频率,其余参数保持不变,模拟得到如图4 忆阻V-I 图:
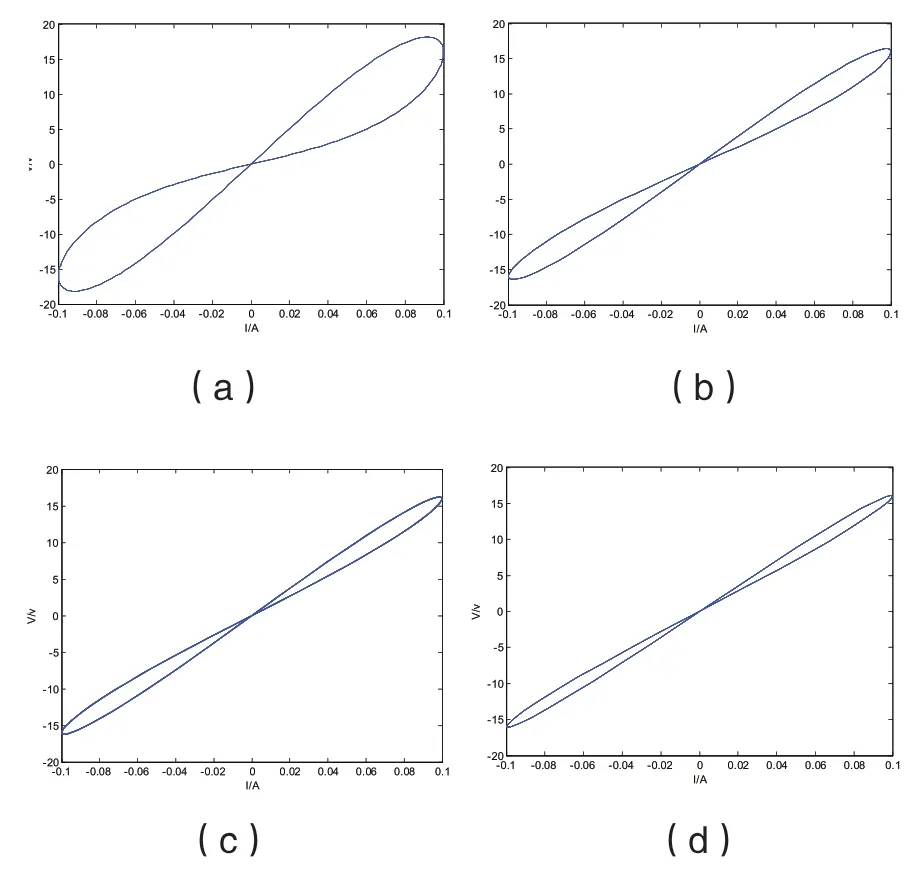
图4 忆阻M=aq(t)+b 磁滞旁瓣面积随激励电流频率变化的V-I 图:(a)ω=2 π 时,元件V-I 图;(b)ω=5 π时,元件V-I 图;(c)ω=7 π 时,元件V-I 图;(d)ω=10π 时,元件V-I 图
即,V-I 图磁滞旁瓣面积随着激励频率的增加而减少。
继续增加驱动电流频率,忆阻V-I 图变化如图5 所示:从图5 可以看出,当激励频率继续增加,磁滞旁瓣面积持续减小;当激励频率趋近于无限大时,磁滞回线收缩为一个单值函数,如图5(d)所示。

图5 忆阻M=aq(t)+b 激励频率趋近于无穷时V-I 变化图:(a)ω=15π时,V-I 图;(b)ω=20π时,V-I 图;(c)ω=30π时,V-I 图;(d)ω=100π时,V-I 图
如若已知一元件为忆阻,则必具有图3、图4、图5 的三个基本特征;反过来,若一元件具备这三个特征,则可判定其为忆阻。
3 忆阻的数学理论模型及性质研究
随着忆阻研究的发展,多种忆阻模型被相继提出:2007 年,James C.Scott[12]用有机化合物构造出了忆阻器;2008 年,加州大学的Yuriy V.Pershin 和Massimiliano Di.Ventra 提出了自旋电子忆阻器器件;2009 年,XB.Wang[13]提出自旋忆阻器;2012 年,D.J.Kim[14]用铁电隧道结构造出了忆阻器,同年,Ioannis Vourkas 和Georgios Ch.Sirakoulis[15]提出阈值开关忆阻器;2013 年,Shahar Kvatinsky 等[16]提出了电压/电流自适应忆阻器;2014 年,Ahmad Muqeem.Sheri[17]等提出了基于Al/Pr0.7Ca0.3MnO3(PCMO)的忆阻器;2015 年,Shinhyun Choi[18]提出基于TaOx的忆阻器;2017 年,Yang Zhang[19]提出基于Ag/AgInSbTe/Ta(AIST)的忆阻器,以及Gang Dou[20]提出基于Sr0.95Ba0.05TiO3(SBT)的忆阻器等等。为了便于研究忆阻特性,一些忆阻的仿真模型也相继被提出:Dmitri B.Strukov[1]根据流经忆阻器电荷量与元件掺杂区域宽度的关系提出了线性杂质漂移忆阻模型;Makoto Itoh[21]提出一种分段线性的忆阻器模型,其本构变量 q 和 φ 的关系是分段线性的;陆益民[22]等人提出一种磁控忆阻器模型,并使用该模型构造出Van der pol 振荡器;俞清[23]等人提出了一阶有源广义忆阻模型。Alon Ascoli[24]提出一种广义边界条件的忆阻器模型;包伯成[25-26]等人更是利用二极管桥,放大器等元件搭建了模拟忆阻的等效电路模型。
参考大量相关资料,学者提出的忆阻模型可归纳为三种数学理论模型:分段线性函数[27]、二次非线性函数[28-29]和三次非线性函数[30-32]。下面将对这三类忆阻模型进行深入探讨和研究。
分段线性函数是被人广泛认可的忆阻数学理论模型,分段线性荷控忆阻数学关系如下:
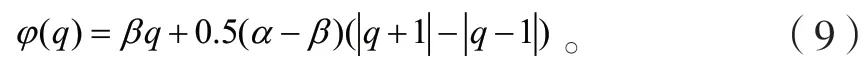
相应的忆阻为:

分段线性磁控忆阻数学关系为:
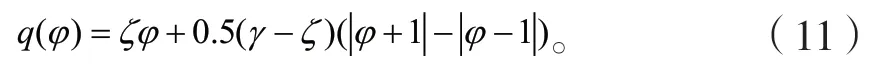
相应的忆导为:
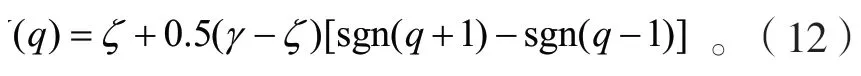
其中,α,β、γ、ζ为正常数,且α≠β,γ≠ζ;sgn(n)为符号函数。则其特征曲线如图6 所示:
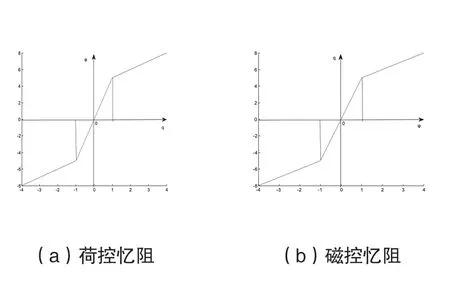
图6 分段线性忆阻特性曲线
二次非线性磁控忆阻数学模型为:

与此对应的忆导为:

三次非线性磁控忆阻的数学模型为:

忆导为:

同样γ ,ζ都为正常数。
可得非线性磁控忆阻的特性曲线和忆导关系曲线如图7 所示:

图7 二次非线性磁控忆阻特性曲线与忆导关系曲线
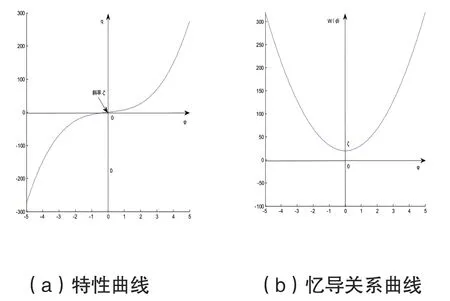
图8 三次非线性磁控忆阻特性曲线与忆导关系曲线
从图7(b)可以看出,忆导有负值,因此二次非线性磁控忆阻为有源磁控忆阻,可以等效为一个无源忆阻和负电阻。
设ζ=0.5mS,γ=30S/Wb2,忆阻内部初始条件φ0=0Wb,驱动电压为V=Vmaxsin(ωt),其中Vmax为电压振幅,ω为角频率;当Vmax=2V,ω=2π时,因为磁通量由忆阻两端的电压决定,利用Matlab 代换出磁通量的时间函数从而模拟得到二次非线性磁控忆阻电压与时间图及电流与时间图,见图9:

图9 二次非线性磁控忆阻电压时间图和电流时间图
从图9 可以看出,电流与电压频率相同,但是电流时间图的波形发生改变。
当电压振幅或者角频率改变,其余参数保持不变时,利用Matlab 数值仿真得到二次非线性磁控忆阻的V-I 图,见图10:
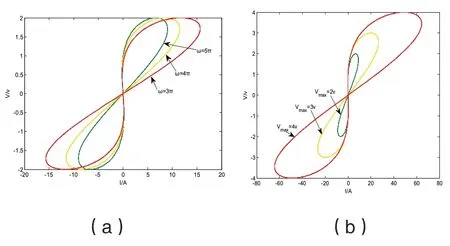
图10 二次非线性磁控忆阻不同条件下的V-I 图:(a)电压振幅恒定 Vmax=2v,角频率不同时的V-I 电压时间图;(b)角频率恒定 ω=2 π,电压振幅不同时的V-I 图
从图10 可以看出二次非线性磁控忆阻V-I 图为一条在原点紧缩的磁滞回线,且磁滞旁瓣面积随着驱动电压频率的增加而减小,符合前面所阐述的忆阻通性;不仅如此,当改变驱动电压振幅时,磁滞旁瓣面积随着驱动电压振幅的增加而增加。
选用参数:ζ=0.5mS,γ=30S/Wb2,忆阻内部初始条件φ0=0Wb,驱动电压Vmax=2v,ω=2π时,利用Matlab 数值仿真得到三次非线性磁控忆阻电压与时间图及电流与时间图,见图11:从图11 可以看出,电流频率仍然与电压频率相同,电流的波形发生改变,且对比图9(b)与图11(b)发现三次非线性磁控忆阻的电流图波形与二次非线性电流图波形类似,但又有稍许不同。
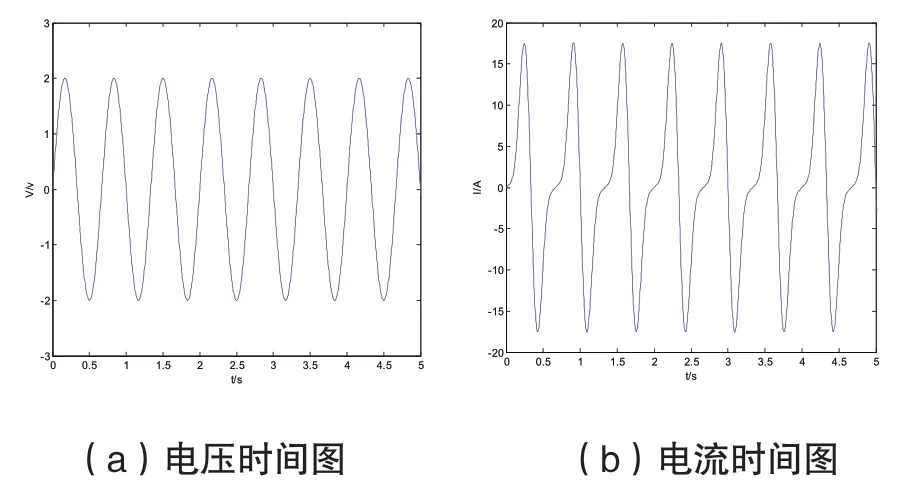
图11 三次非线性磁控忆阻电压时间图和电流时间图
当电压振幅或者角频率改变,其余参数保持不变时,利用Matlab 数值仿真得到三次非线性磁控忆阻的V-I 图,见图12:
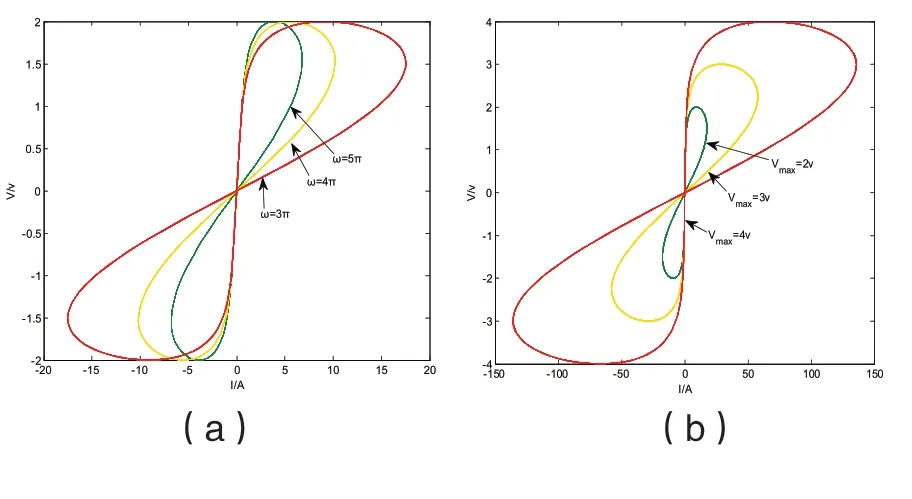
图12 三次非线性磁控忆阻不同条件下的V-I 图:(a)电压振幅恒定 Vmax=2v,角频率不同时的V-I 电压时间图;(b)角频率恒定 ω=2 π,电压振幅不同时的V-I 图
因此三次非线性磁控忆阻V-I 图与二次非线性磁控忆阻V-I 图具有相似性质,同样三次非线性磁控忆阻仍然具有忆阻共性。
在这三种理论模型中,非线性忆阻最能简单表达电荷与磁通量之间的非线性关系,因而广泛被学者认同和应用。
4 结论
忆阻是近年来一个新兴的研究方向,由于发展历史相对较短,许多理论不成熟、不完善、不系统。本文参考大量的外文文献,对忆阻的诸多理论进行归纳、综述,并对忆阻的重要性质进行程序模拟仿真重现。将忆阻模型归纳为三种数学理论模型:分段线性函数、二次非线性函数和三次非线性函数,并对这三种理论模型进行详细阐述,模拟得到每种理论模型的特性曲线以及忆导关系曲线。对其中性质较为复杂的二次和三次非线性磁控忆阻性质进行研究,数值仿真了其电流时间图、电压时间图以及参数变化时的V-I 图;从仿真图可以看出,二次和三次非线性磁控忆阻的电流频率都与电压频率相同,电流的波形类似且都发生改变,V-I 图的磁滞旁瓣面积都随着驱动电压频率的增加而减小,符合忆阻通性,不仅如此,磁滞旁瓣面积还都随着驱动电压振幅的增加而增加。
