三体船波浪增阻与纵向运动数值模拟及试验研究

2021-02-25李昂李云波

哈尔滨工程大学学报 2021年1期

李昂，李云波

(1.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001； 2.上海海事大学海洋科学工程学院，上海 201306)

三体船在合理的主片体布局下，相比于单体船和双体船，在中高航速下具有良好的阻力性能。而在耐波性方面，由于2个侧片体的存在，三体船也具有优良的稳定性以及耐波性能，成为极具应用前景的新船型。海上航行的船舶通常会遭遇波浪，船舶在波浪中的增阻会导致主机功率的增加。如何精确地预报船舶在波浪中的增阻非常重要。在过去的几十年里，波浪增阻以及船舶运动问题已经通过模型试验以及数值计算方法进行了广泛的研究。

模型试验方法包括对60系列[1]和S175集装箱船[2]、Wigley船型[3]以及KVLCC2船型[4]的波浪增阻问题的研究。对于三体船型波浪增阻的试验研究相对较少。基于势流理论方法研究波浪增阻问题可以主要分为远场方法[5]、近场方法[6]以及Rankine源法[7]。随着计算机技术的迅速发展，CFD技术在预报船舶波浪增阻以及运动方面得到广泛的应用，基于粘流理论的CFD数值计算方法考虑了粘性效应，能够计算船舶的大幅运动。国内外研究学者对单体船型进行了大量的CFD计算研究[8-11]，分析了航速、波浪周期、波幅等参数对波浪增阻及运动的影响。吴乘胜等[12]对高速三体船波浪中运动与增阻进行了数值计算研究，分析了侧片体对主船体阻力增加的影响。陈悦等[13]对高速三体船在规则波中的波浪增阻及纵向运动进行了数值仿真研究，并通过与模型试验结果进行对比验证其方法的有效性。国内外对于航速、波陡等参数变化对三体船迎浪规则波中运动带来的非线性的影响研究较少。

本文针对某三体船型在迎浪规则波中的波浪增阻以及纵向运动进行了数值计算和模型试验研究，分析了三体船不同航速下迎浪规则波中波浪增阻和纵向运动响应特性。采用重叠网格和运动域网格方法分别对不同航速下三体船波浪增阻及纵向运动响应进行了数值计算，并通过与船模水池试验结果进行对比分析，探讨了不同网格划分方法对数值计算结果的影响。研究了不同波陡波浪参数对三体船波浪增阻及纵向运动的非线性影响。

1 CFD数值计算方法

1.1 基本控制方程

计算中整个流场属于三维、两相、黏性的不可压缩流体流动。对于湍流的模拟采用雷诺平均法，控制方程为：

(1)

(2)

(3)

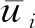
1.2 CFD数值波浪水池

为了模拟三体船周围流场，考虑到计算效率以及计算精度，本文建立了图1所示的长方体计算域。具体计算域的参数设置为：船前1倍船长，船艉3倍船长，船侧1.5倍船长，自由液面以上1倍船长，自由液面以下2倍船长。整个流体计算域关于三体船中体中纵剖面对称，将三体船中体中纵剖面所在平面取为对称平面，侧边边界条件也设置为对称平面。入口、顶部以及底部边界条件设置为速度进口，出口边界条件设置为压力出口。为了避免波浪传播到计算域尾端产生回流而影响整个流场的分布，对波浪进行消波处理，消波区的长度设置为1倍船长。

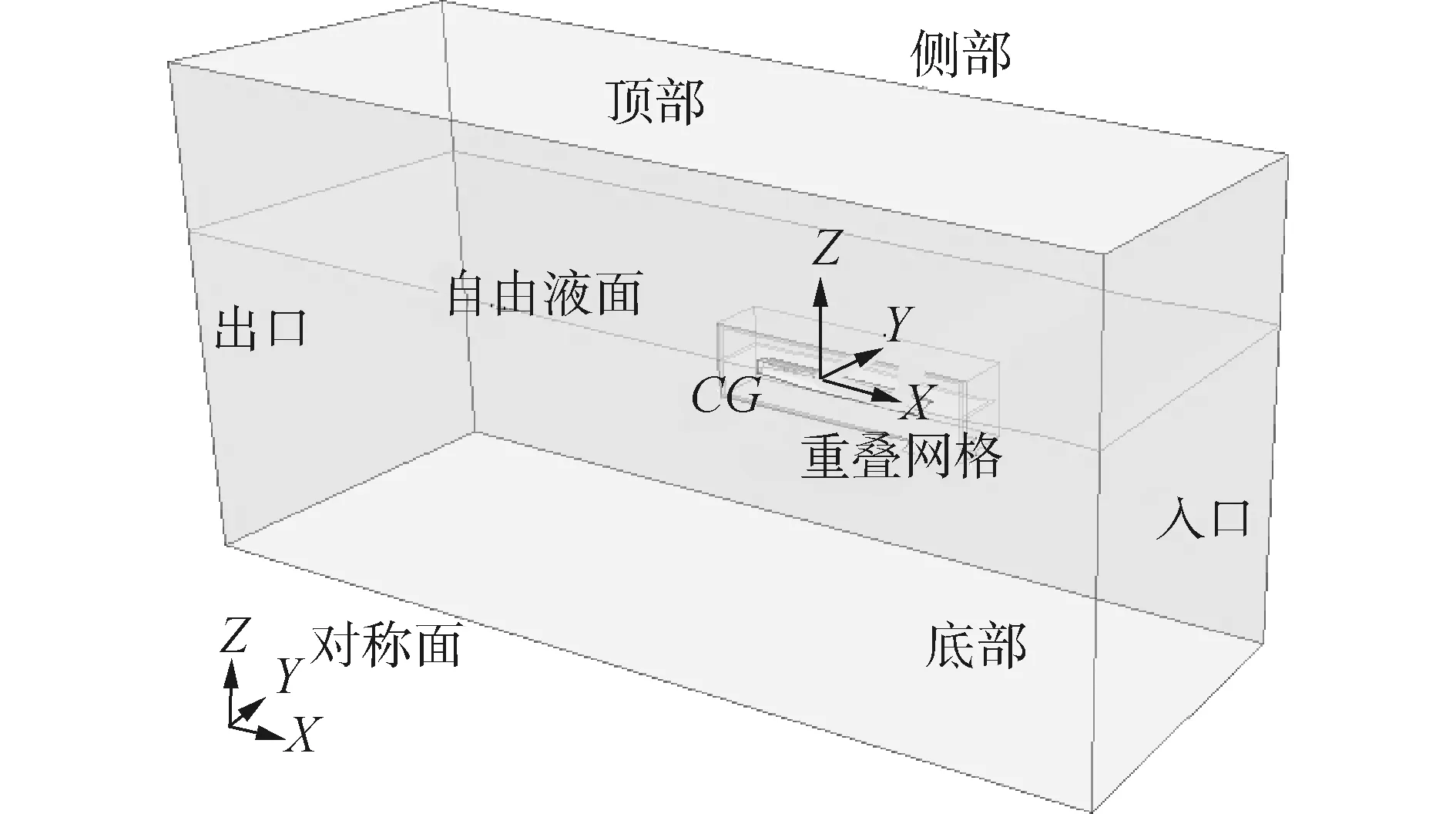
图1 计算域及边界

1.3 数值计算网格模型

网格划分对于模拟细节流场的计算精度以及迭代的收敛性具有较大影响。本文使用重叠网格方法和运动域网格方法对三体船不同航速下静水中阻力及迎浪规则波中纵向运动进行了数值计算。

重叠网格是将物体各运动单元单独划分网格，再嵌入到另一套网格当中，各个子域网格存在重叠、嵌套或覆盖关系，流场信息通过插值的手段在重叠区域边界进行交换和匹配。在运动域网格方法中，整个流体计算域被处理为一个运动的整体。图2为船舶运动过程中，重叠网格以及运动域网格示意图。可以发现，三体船航速较高时，纵向运动响应幅值较大导致自由液面网格变形，导致数值计算精度下降。

图2 重叠网格及运动域网格示意

重叠网格重叠域的尺寸设置为：船前0.15倍船长，船侧、船后及水线以上和水线以下分别为0.2倍船长。为了能够精确捕捉自由液面，在自由液面处进行了网格加密。对于不同波长下三体船波浪增阻及运动的数值计算，计算域的网格划分也有所不同。对于较短波长，对自由液面以及船体周围进行网格加密。图3和图4所示是当傅汝德数Fr为0.353时，波长船长比λ/L=0.50和λ/L=1.60时自由面的网格示意图。在整个波长范围内的数值计算当中，保证单位波长下70～100个网格，单位波高下14～20个网格。

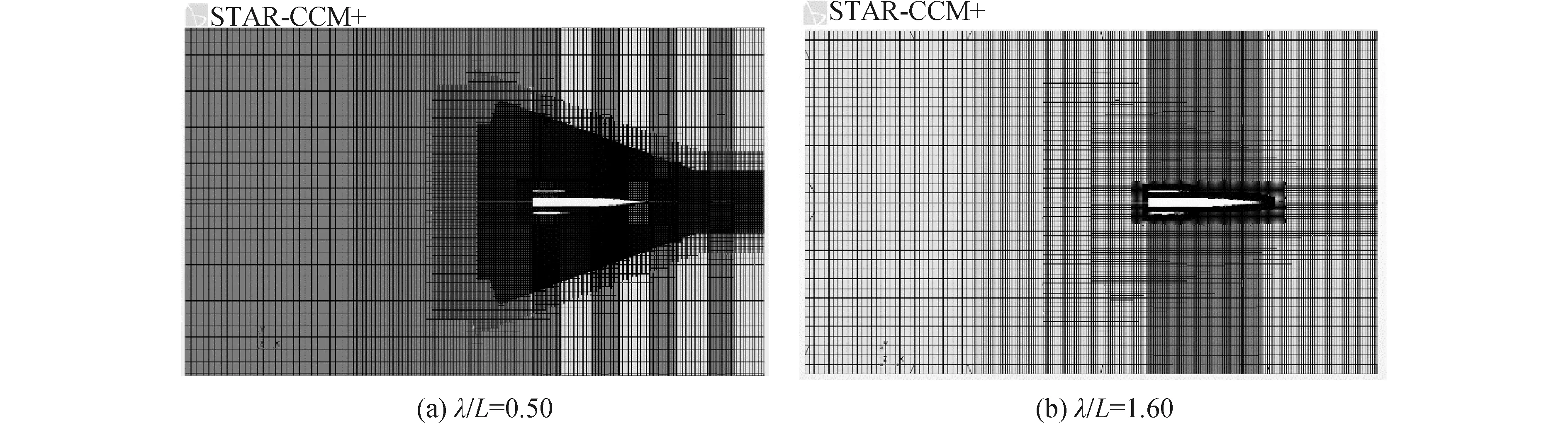
图3 自由面网格划分示意图

2 船模水池试验

2.1 三体船模型参数

三体船模型的主尺度参数如表1所示。其模型示意图如图4所示。

表1 三体船模型主尺度参数

图4 三体船模型示意

2.2 波浪参数及船模试验工况

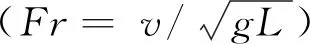
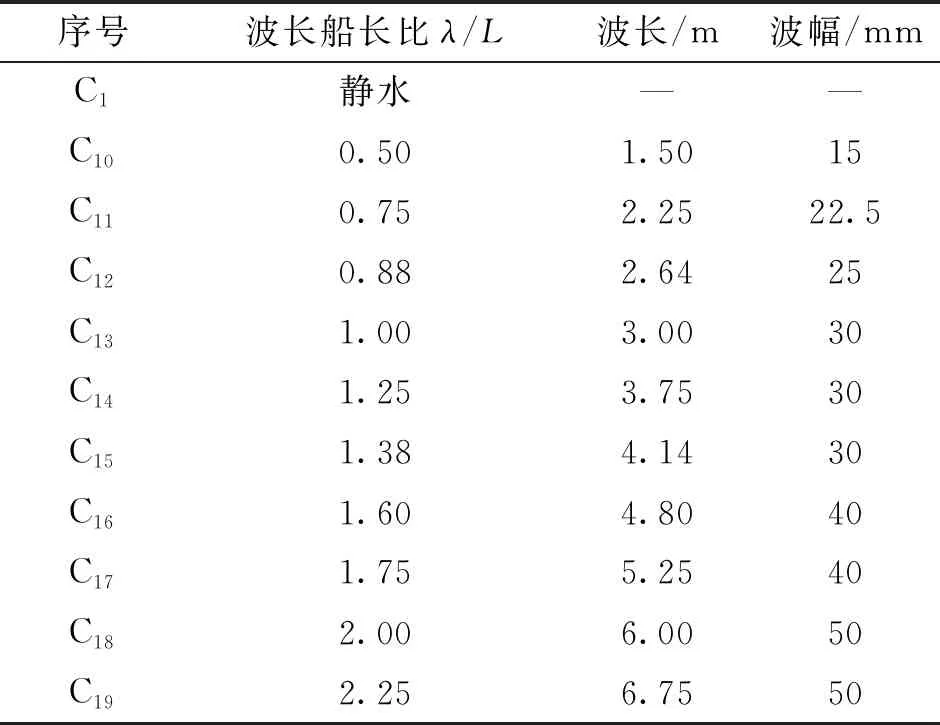
表2 波浪参数(Fr=0.628)

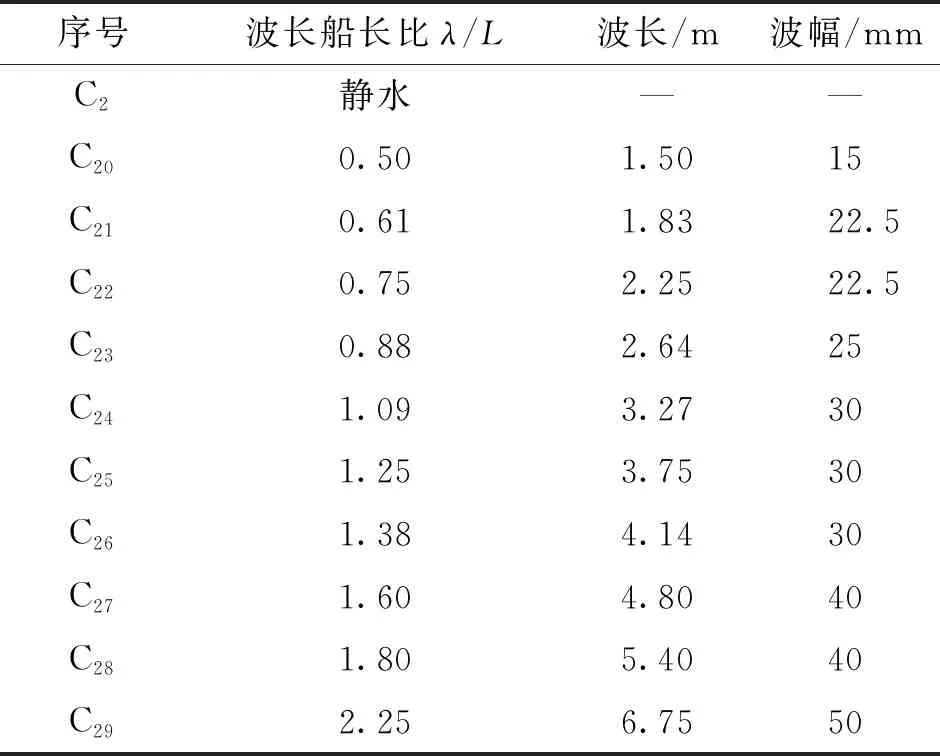
表3 波浪参数(Fr=0.353)

3 数值计算和船模试验结果分析

3.1 三体船静水阻力

为了研究不同网格划分方法对三体船迎浪规则波中波浪增阻及纵向运动响应的影响，本文首先使用重叠网格方法和运动域网格方法对三体船静水阻力进行了数值计算，得到三体船不同航速下法静水阻力计算结果。静水阻力数值计算结果同模型试验结果对比见表4和表5。

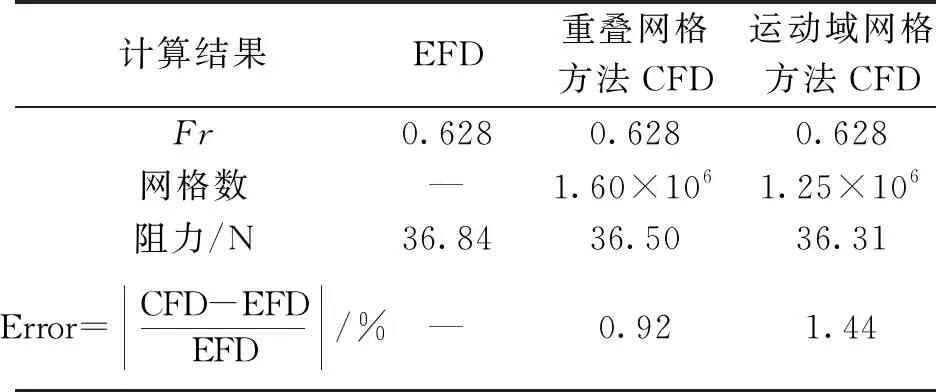
表4 三体船静水阻力(Fr=0.628)

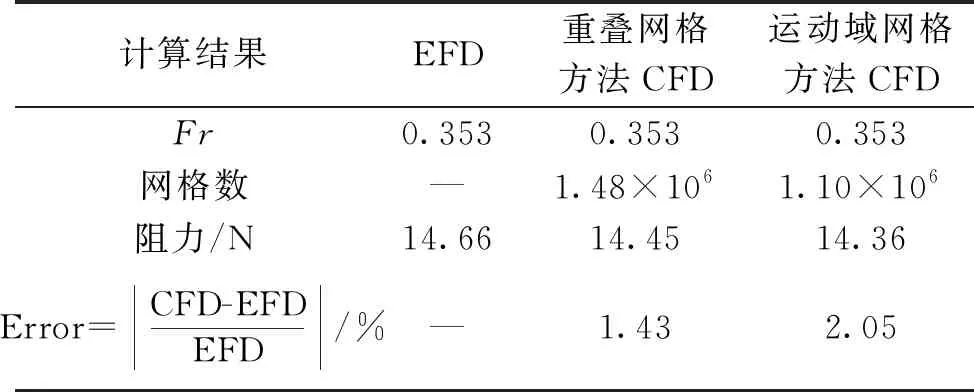
表5 三体船静水阻力(Fr=0.353)

表4所示是使用重叠网格方法和运动域网格方法得到的三体船傅汝德数0.628航速下静水阻力数值计算结果和模型试验结果。表5所示的是使用重叠网格方法和运动域网格方法数值计算得到的三体船傅汝德数0.353航速下静水阻力结果和模型试验结果。有研究表明，船体表面边界第1层网格的无量纲厚度y+值取100可取得较为理想的计算结果[14]。图5所示的是本文研究中三体船船体表面边界第1层网格的无量纲厚度y+沿主、侧体的分布图。整个三体船船体表面边界第1层网格的无量纲厚度y+值在60～140。

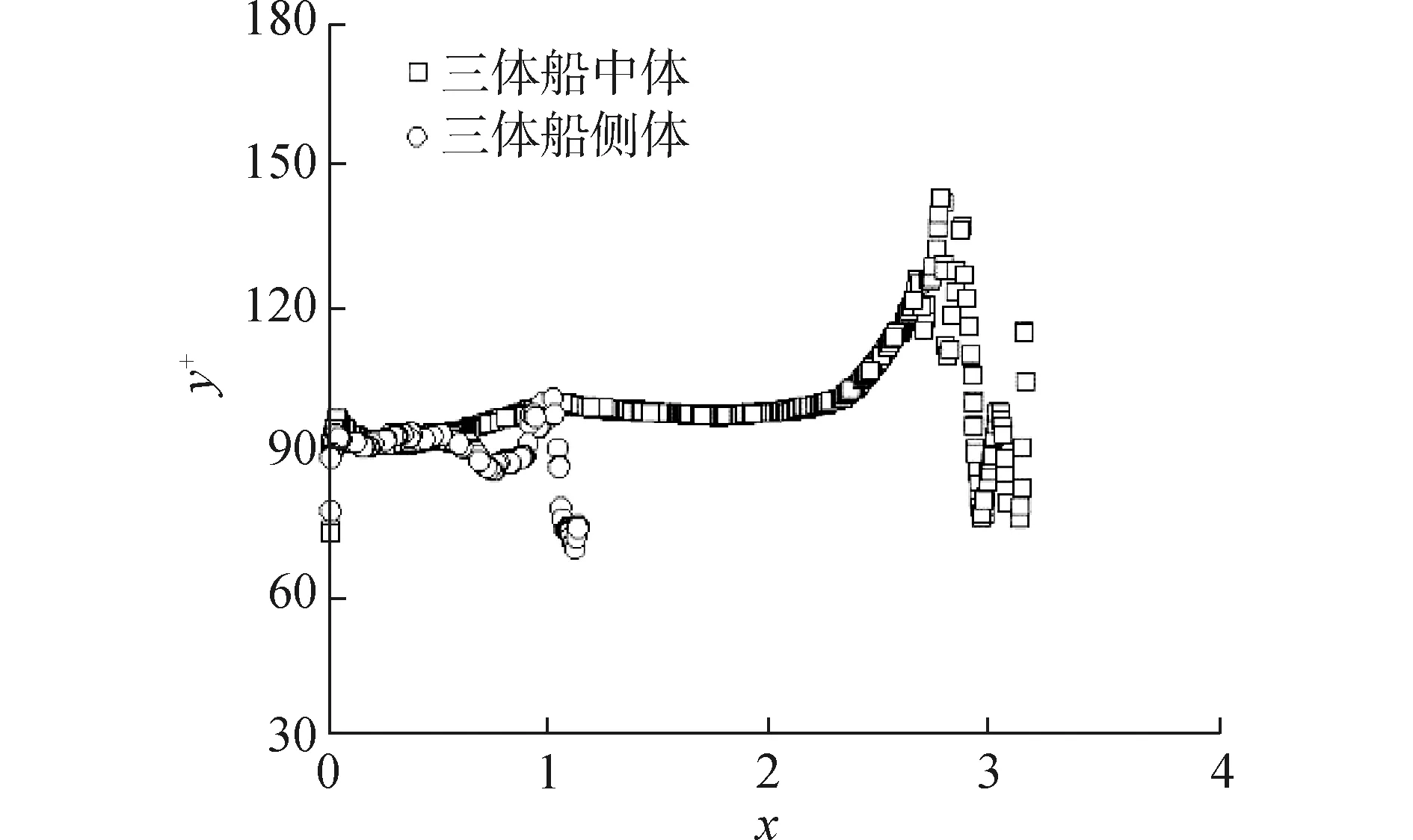
图5 船体表面y+分布

经过分析比较不同傅汝德数下三体船静水阻力数值计算结果与试验结果，重叠网格以及运动域网格方法都可以较为准确地计算三体船不同傅汝德数下的静水阻力。使用重叠网格方法得到的三体船静水阻力计算结果在不同傅汝德数相比于运动域网格方法与模型试验结果误差更小。

3.2 数值造波及三体船波浪增阻与纵向运动

为了得到三体船的波浪增阻及纵向运动响应，并探讨不同网格划分方法对数值计算结果的影响。本文使用重叠网格方法和运动域网格方法数值计算了三体船在不同航速下迎浪规则波中的运动响应以及总阻力。通过计算不同波浪参数条件下三体船的总阻力与静水阻力的差值，得到三体船在迎浪规则波中运动时的波浪增阻。为了验证数值计算域中所造波浪的精度，在三体船船前0.5倍水线长处设置波高监测点[15]，图6所示的是波长船长比λ/L=1.38时，波高监测点数值计算得到的波浪幅值时历曲线。经过傅里叶级数表达得到的一阶波浪幅值为0.028 4 m，与理论波幅的误差为5.33%。

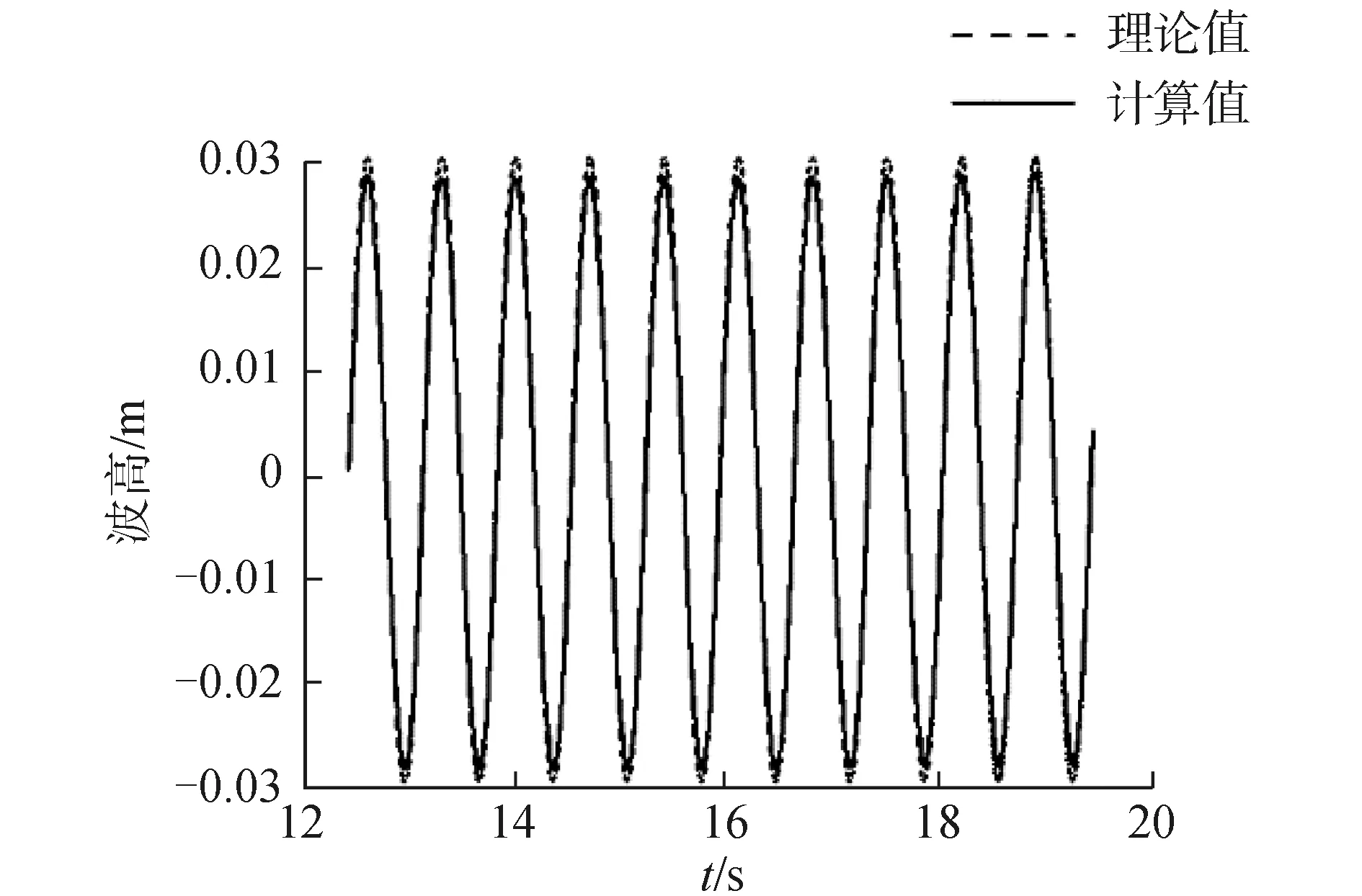
图6 波高检测点波幅时历曲线

使用重叠网格方法以及运动域网格方法数值计算得到的三体船不同航速下升沉、纵摇运动响应曲线以及波浪增阻计算结果与模型试验结果如图7～图12所示。

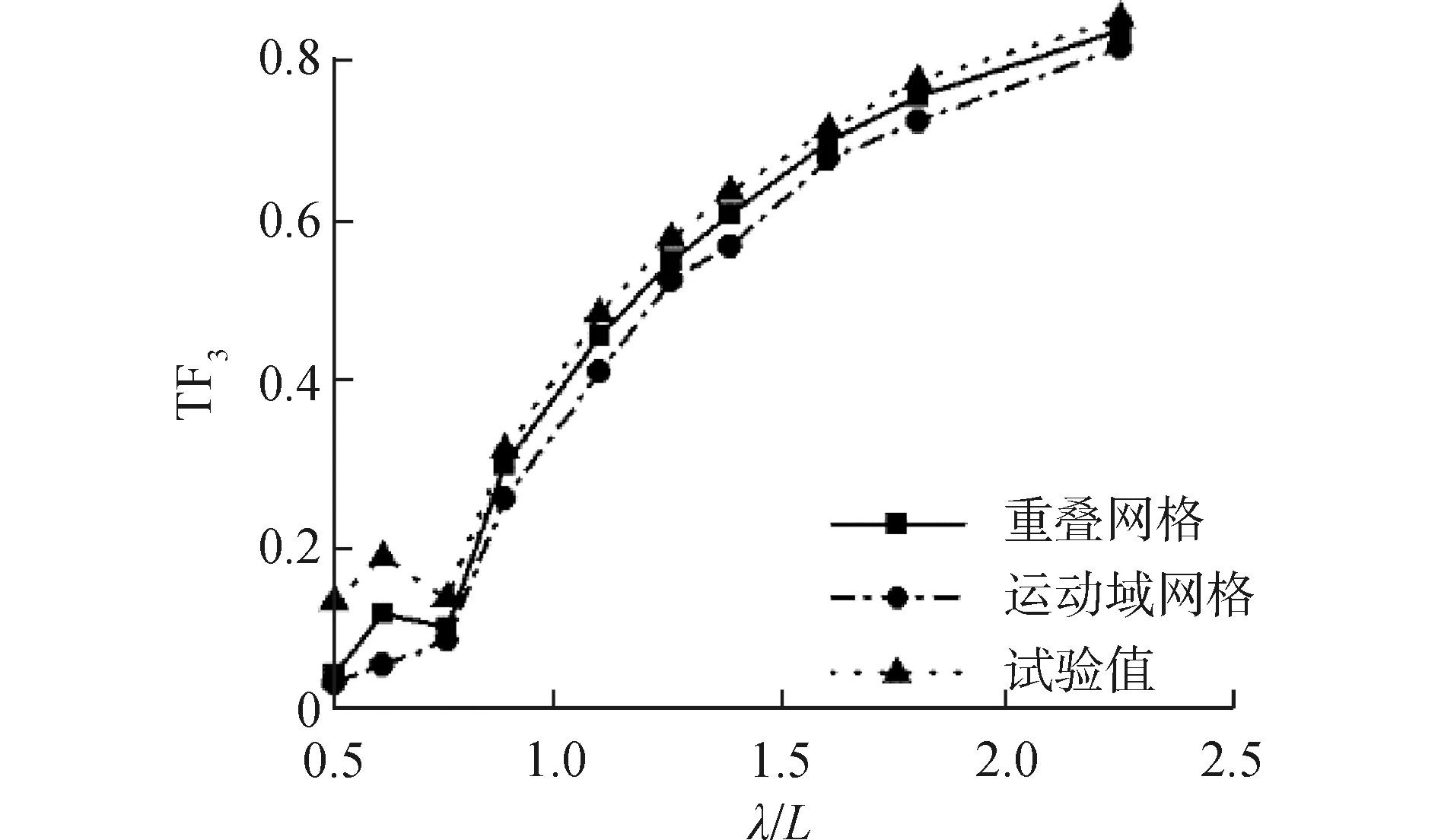
图7 较低航速三体船升沉运动响应曲线(Fr=0.353)

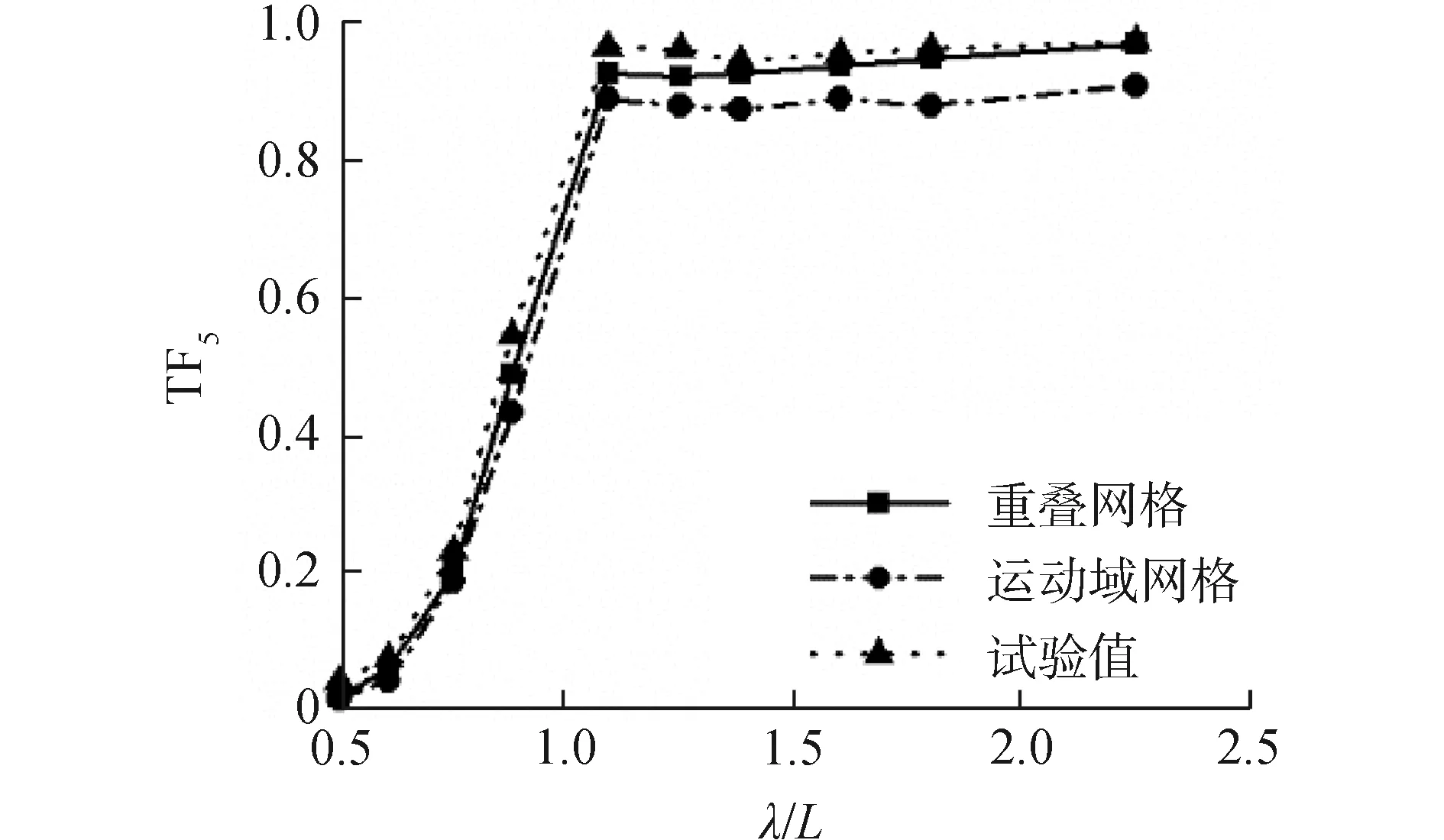
图8 较低航速三体船纵摇运动响应曲线(Fr=0.353)

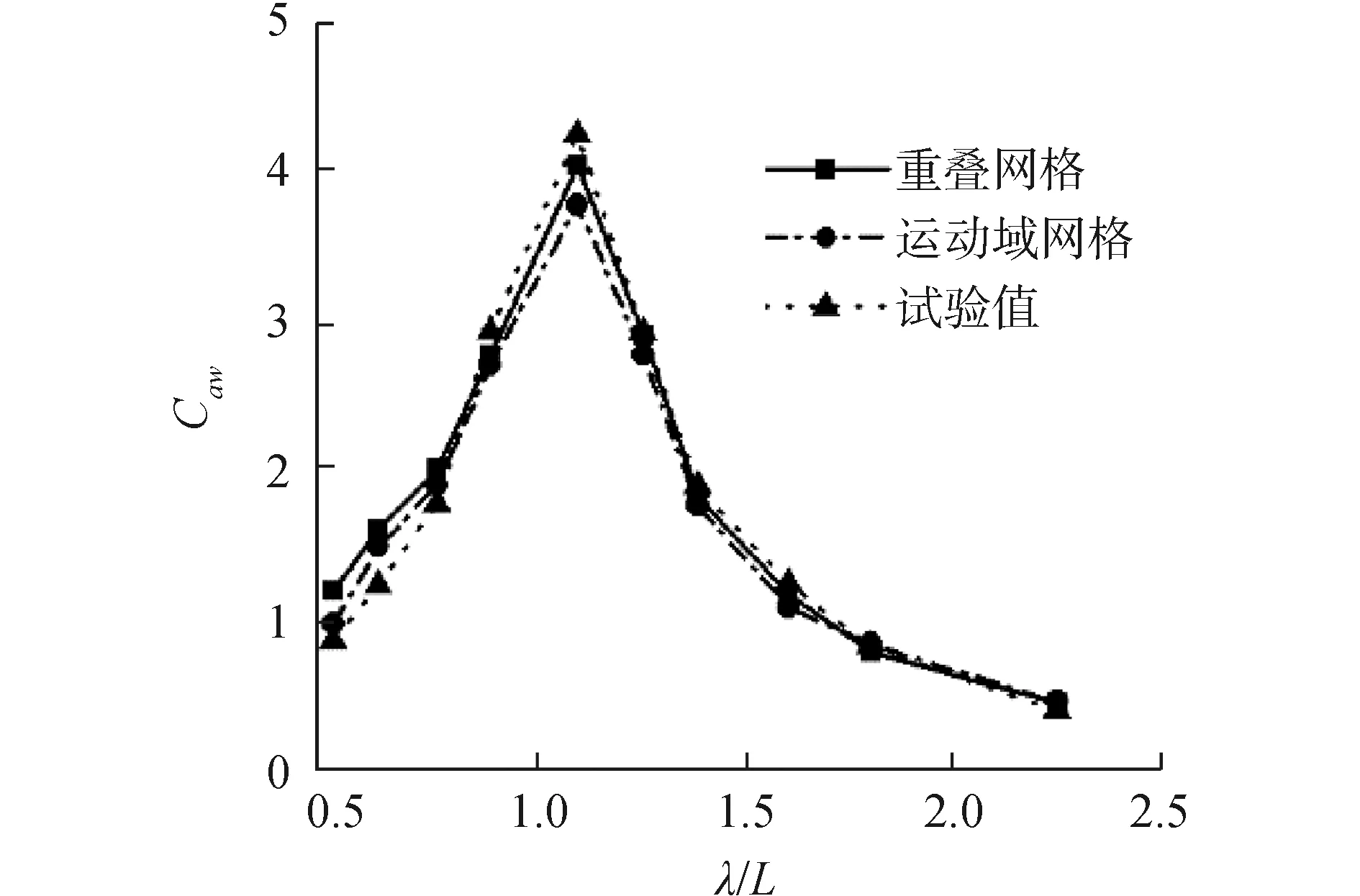
图9 较低航速三体船波浪增阻曲线(Fr=0.353)

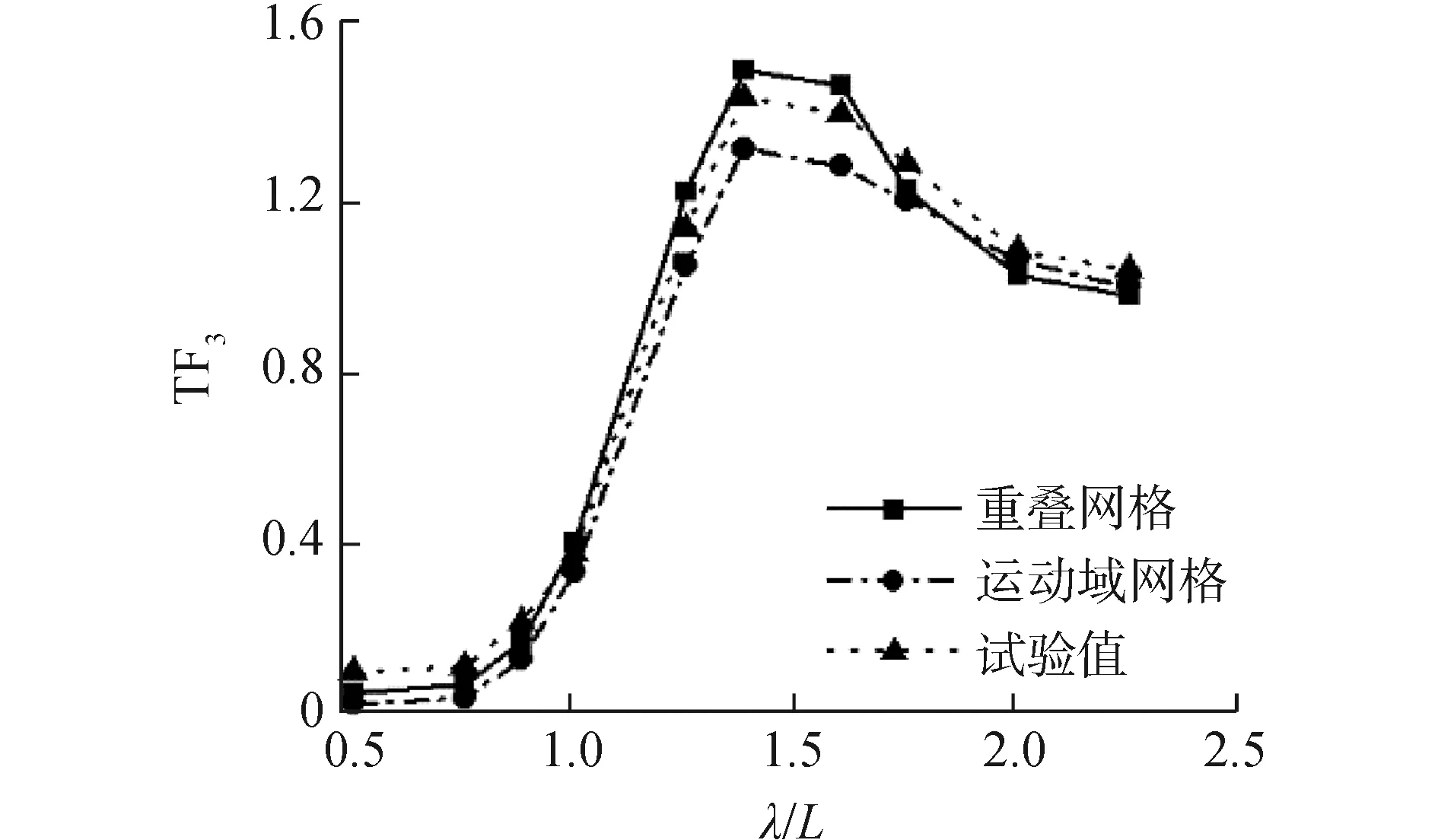
图10 高速三体船升沉运动响应曲线(Fr=0.628)

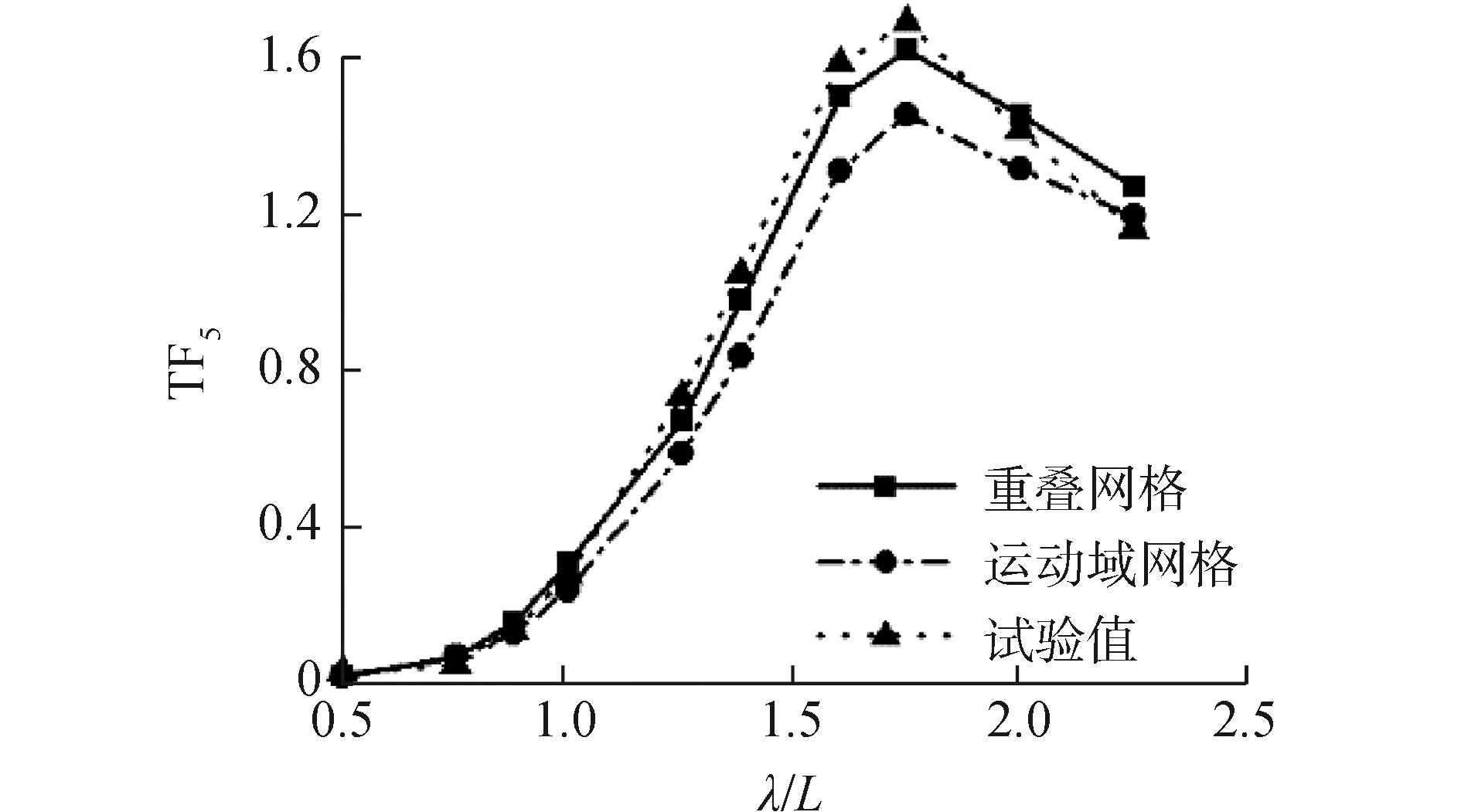
图11 高速三体船纵摇运动响应曲线(Fr=0.628)

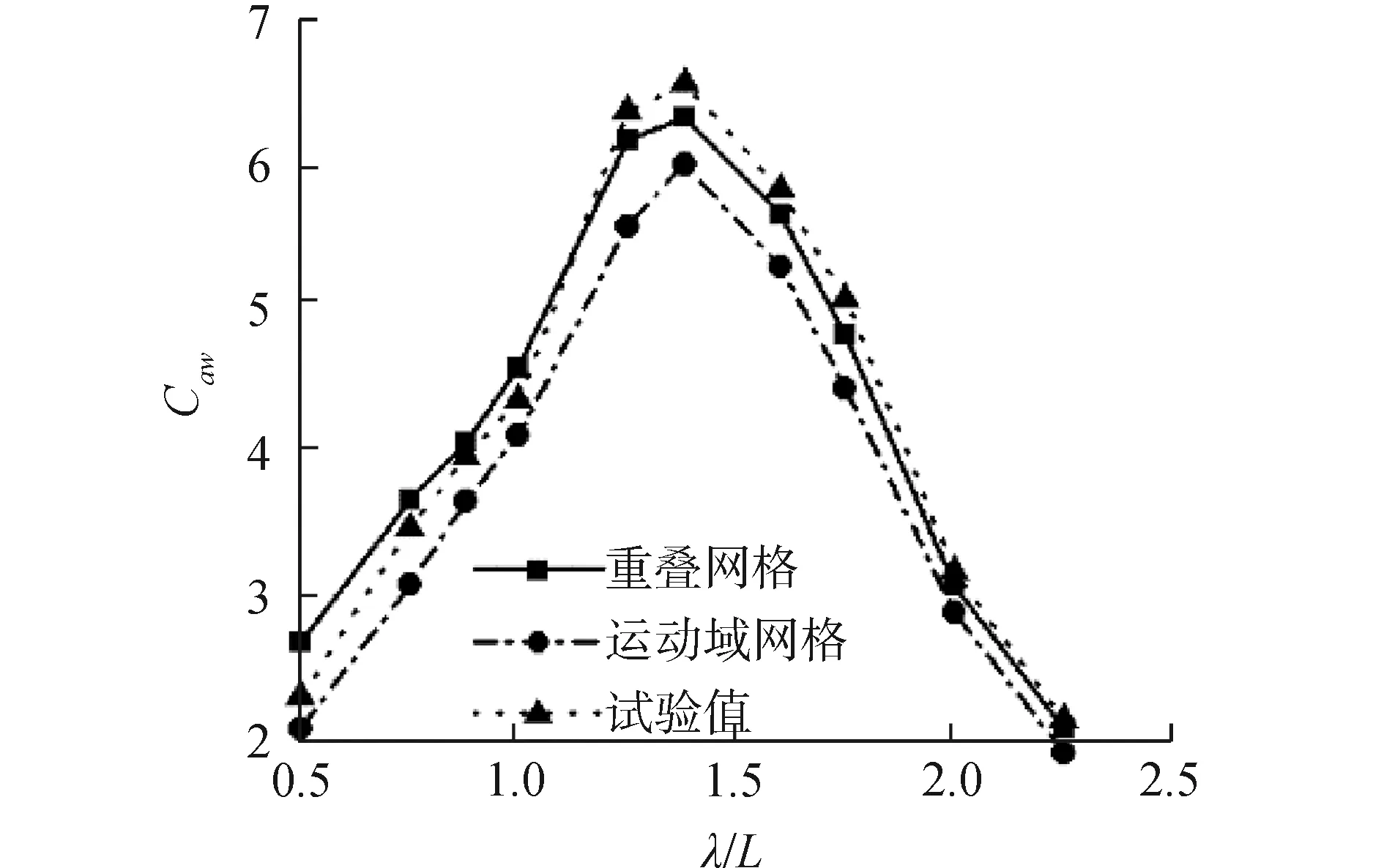
图12 高速三体船波浪增阻曲线(Fr=0.628)

图7～12分别表示三体船在迎浪规则波中数值计算和模型试验的升沉、纵摇运动响应以及波浪增阻曲线。三体船迎浪规则波中升沉、纵摇运动响应的无因次化公式表示为：

(4)

(5)

式中：Za表示升沉运动响应幅值；φa表示纵摇运动响应幅值；ζa表示规则波波幅；k表示波数。

通过三体船在迎浪规则波中的总阻力减去三体船在静水中的阻力，得到三体船在波浪中的增阻。波浪增阻的计算公式及其无因次化公式为：

(6)

(7)

图7～9表示的是傅汝德数为0.353时迎浪规则波中升沉、纵摇运动响应及波浪增阻。数值计算结果与船模试验结果对比可见，使用重叠网格方法与运动域网格方法得到的三体船升沉、纵摇运动响应以及波浪增阻与船模水池试验结果有相同的变化趋势；使用运动域网格计算方法并没有捕捉到在波长船长比λ/L=0.61附近出现的小峰值点；使用运动域网格计算方法得到的纵向运动响应幅值以及波浪增阻相比于重叠网格计算方法得到的纵向运动响应幅值及波浪增阻较小，重叠网格方法数值计算结果误差更小。

图10～12是傅汝德数为0.628时迎浪规则波中的升沉、纵摇运动响应及波浪增阻。由数值计算结果与船模试验结果对比可见，使用重叠网格方法与运动域网格方法数值计算得到的三体船升沉、纵摇运动响应以及波浪增阻与船模水池试验结果有着相同的变化趋势，在运动幅值出现的波长船长比(λ/L=1.60)附近的共振区内，由于三体船纵向运动响应幅值较大，运动域网格计算方法中自由面网格的变形较大，数值计算误差相对较大。得到的升沉、纵摇运动响应幅值相比于重叠网格计算方法较小，使用重叠网格计算方法得到的数值计算结果误差更小。从三体船波浪增阻曲线来看，在整个波长范围内，使用运动域网格计算方法得到的波浪增阻误差较大。综上，重叠网格方法更适于计算高航速三体船纵向运动响应及波浪增阻。因此，后续探讨波陡对三体船波浪增阻及纵向运动的影响时，均采用重叠网格计算方法。

3.3 波陡对三体船波浪增阻及纵向运动的影响

本文对λ/L=0.50和λ/L=1.60波长、傅汝德数0.353和0.628，研究了三体船波浪增阻和纵向运动与波陡(H/λ)的关系，具体波浪参数见表6和表7。数值计算得到的不同航速、不同波长下三体船波浪增阻及纵向运动响应曲线以及波陡对三体船波浪增阻及纵向运动影响见图13～18。

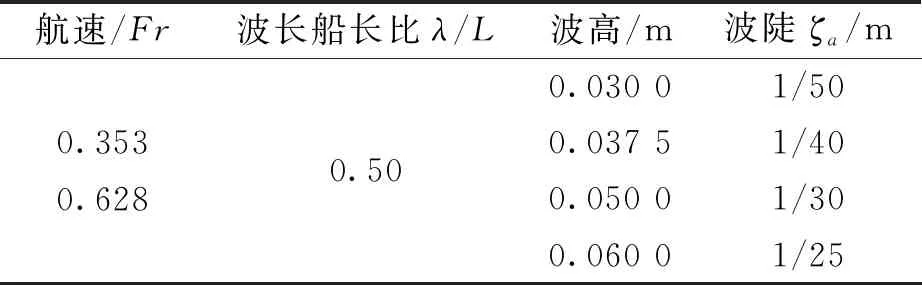
表6 波浪参数(λ/L=0.50)

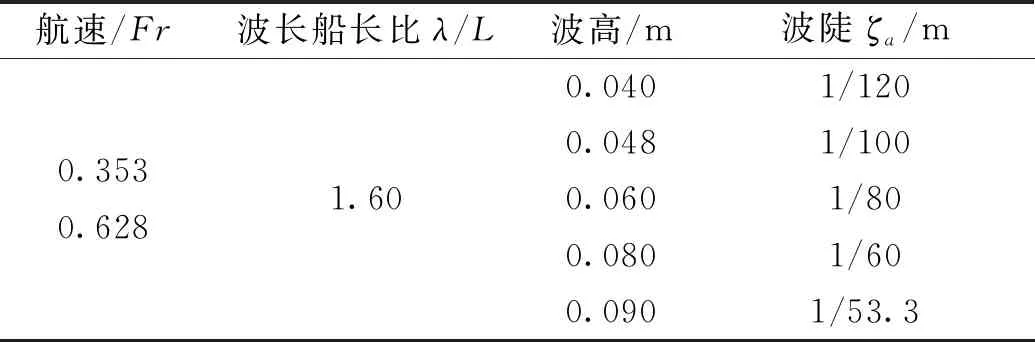
表7 波浪参数(λ/L=1.60)

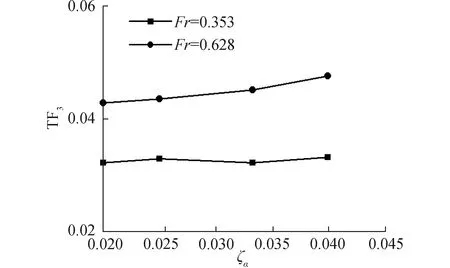
图13 小波长不同波陡升沉运动响应曲线

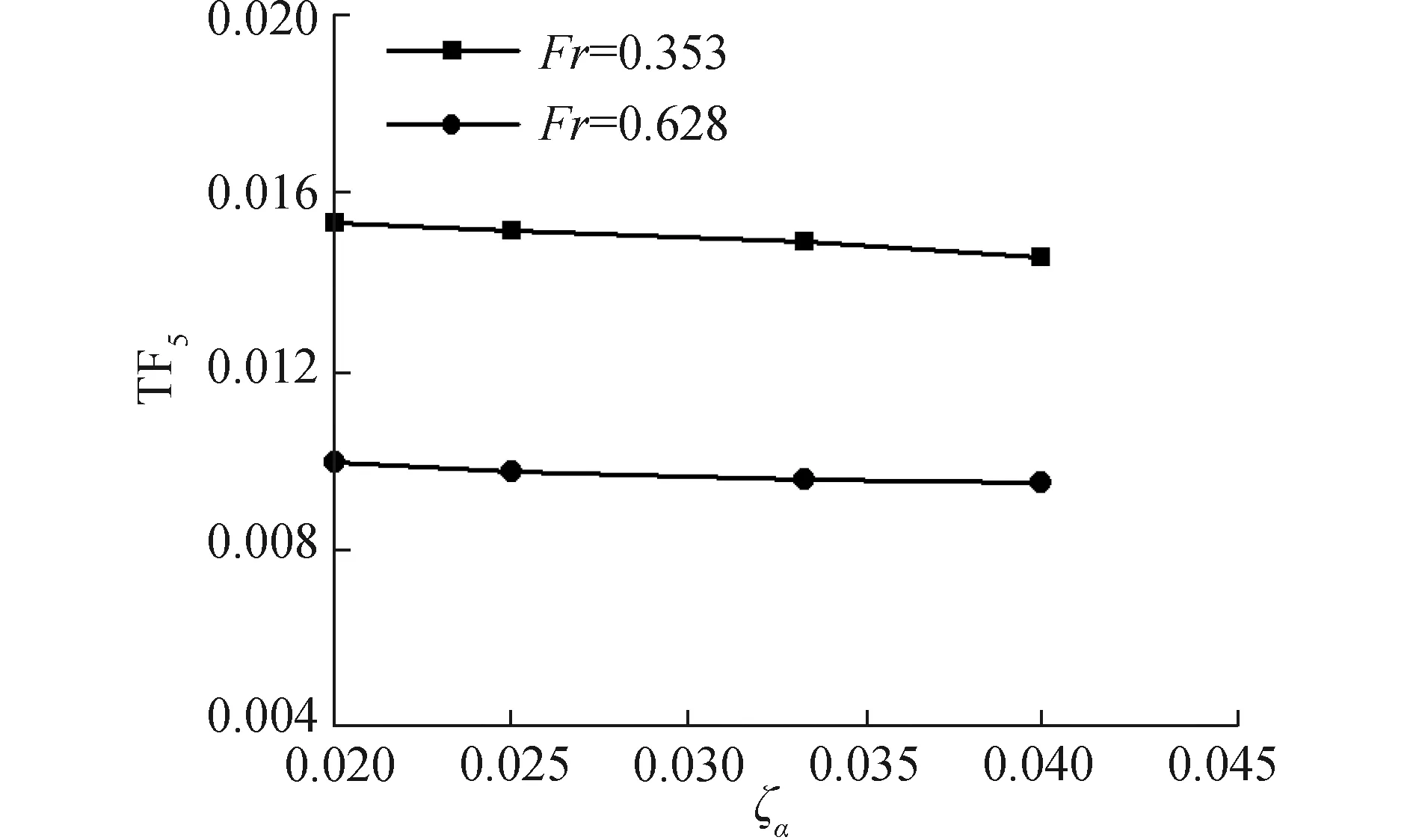
图14 小波长不同波陡三体船纵摇运动

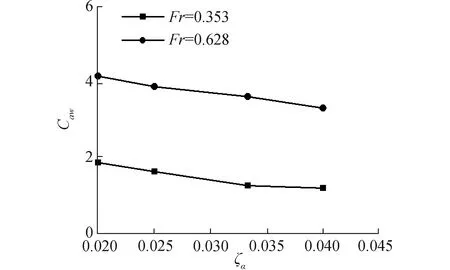
图15 小波长不同波陡三体船波浪增阻曲线

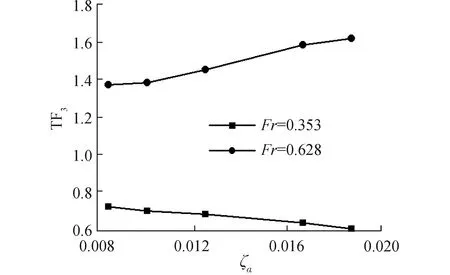
图16 大波长不同波陡升沉运动响应曲线

图13～15表示的是傅汝德数为0.353和0.628下短波λ/L=0.50中三体船升沉、纵摇运动响应以及波浪增阻随波陡变化的数值计算结果。由图13可得，三体船在较低航速升沉运动响应随波陡的增加变化不大，较高航速升沉运动响应结果随波陡的增加而增加，表现出高航速下的非线性；图14表示在不同航速下，三体船纵摇运动响应随波陡增加的变化不大，有减小的趋势。高航速三体船在短波λ/L=0.50中波陡变化并没有对纵摇运动产生强烈的非线性影响；由图15可见，高航速时，三体船的波浪增阻系数较大，随着波陡的增加，波浪增阻系数在不同航速下都有减小的趋势，表现出明显的非线性特征。

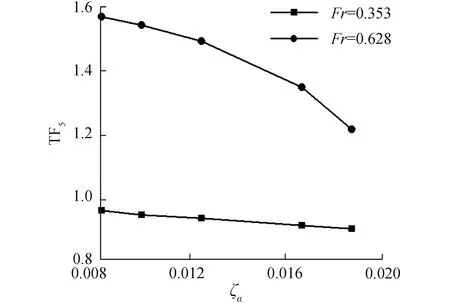
图17 大波长不同波陡纵摇运动响应曲线

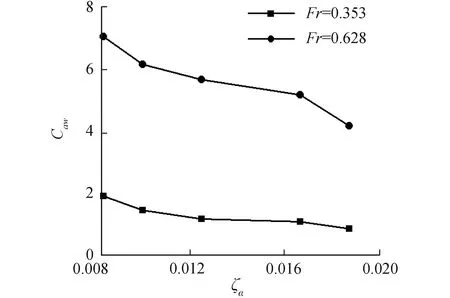
图18 大波长不同波陡波浪增阻曲线

图16～18表示的是傅汝德数为0.353和0.628航速下得到的在长波λ/L=1.60中三体船升沉、纵摇运动响应以及波浪增阻随波陡变化的数值计算结果。图16表示三体船在较低航速，升沉运动响应随波陡的增加有减小的趋势，相比于短波λ/L=0.50非线性增强，对于较高航速，升沉运动响应结果随波陡的增加而增加，表现出高航速下的非线性，并相对于短波λ/L=0.50非线性更加明显；图17表示三体船在较低航速，纵摇运动响应结果随波陡的增加有减小的趋势，同短波λ/L=0.50类似，非线性特征并不明显；对于较高航速时，纵摇运动响应随着波陡的增加有明显的减小，表现出强烈的非线性特征；图18表示高航速时，三体船的波浪增阻系数较大，随着波陡的增加，波浪增阻系数在不同航速下均有减小的趋势，表现出较强的非线性，相比于短波λ/L=0.50，非线性特征更加明显。