基于粒子群优化案例推理的RH终点温度预测

2021-02-25江典蔚刘惠康曹宇轩杨成威

仪表技术与传感器 2021年1期

江典蔚，刘惠康，曹宇轩，杨成威

(1.武汉科技大学信息科学与工程学院，湖北武汉 430081；2.宝钢股份中央研究院武汉分院，湖北武汉 430080)

0 引言

钢铁产业作为国民经济的支柱产业，占据着极其重要的地位，随着时代的进步，科技的创新，传统炼钢技术与产品已经越来越难以满足如今多元的需求。对于炉外精炼国内钢铁厂目前还基本采用人工操作的方式，RH炉作为炉外精炼的关键部分，若能精确的预测出当前温度则可以减少冶炼周期，降低不必要的成本和能耗。由于RH炉在冶炼过程中，需要考虑到各式各样的因素，因此有必要深入分析影响RH炉钢水终点温度的各种因素；删除影响较小的因素，实施属性约简，然后面向一定的数据驱动模型来优化影响因素的权重；最后，基于被处理后属性和权重值，再由能量守恒从而建立钢水终端温度预测模型，以实现RH钢水终点温度的预测。本文主要采用多元线性回归来简化过于庞杂的属性，利用粒子群算法优化影响因素权重[1]，从而利用粒子群优化案例推理来预测钢温，并与多元线性回归、BP神经网络和一般案例推理的预测结果进行比较。

1 粒子群优化案例推理方法

一般案例推理(CBR)基于相似度计算，缺乏问题影响因素的选择方法和属性权重的计算方法，直接限制了其在解决具体问题时的准确性[2]。因此本文提出利用多元线性回归和粒子群优化来解决这一问题。

1.1 一般案例推理方法

案例推理作为一种通过搜索相似历史案例来获取解决方案的数据挖掘方法，在机械、航天、医疗、冶金等领域得到了广泛的应用。一般的案例推理方法由以下4个步骤组成。

一般基于案例的推理方法实现过程如图1所示。案例搜索和重用是一般案例推理的基本步骤。首先，需要处理案例库和问题集的数据。数据处理采用0-1归一化处理方法，具体如下：

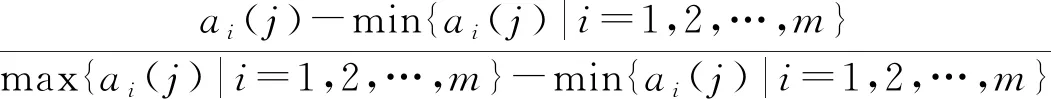
(1)

式中：max{ai(j)|i=1,2,…,m}为数据中的最大值；min{ai(j)|i=1,2,…,m}为数据中的最小值；ai(j)为数据归一化前的值；si(j)为数据归一化后的值。

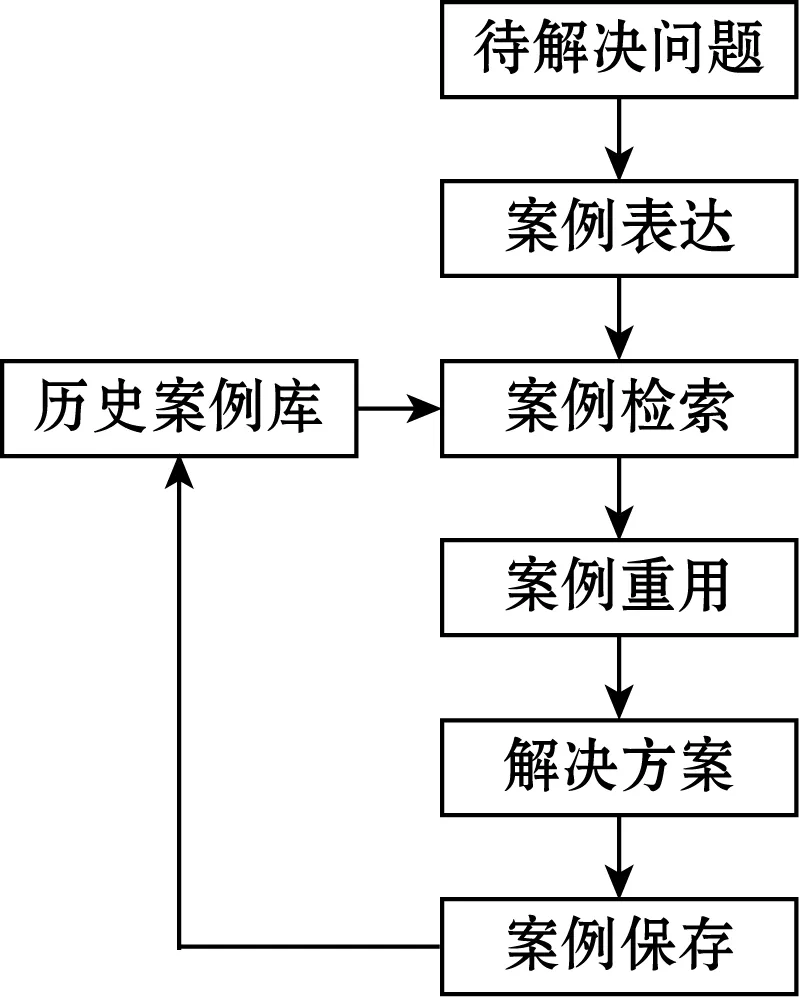
图1 一般案例推理方法的实现过程

然后，确定相似度计算方法。本文采用优化后的灰色关联相似度。假设问题的情况是S0，现有的案例库是{Si|i=1,2,3,…,m}，m是现有案例的数量，那么在n维空间中设置的现有案例中，S0与每个Si之间的灰色相似度为：

(2)

式中Gd[s0(j),si(j)]为S0和Si在特征向量的第j个特征的灰度距离，

(3)

式中Gs[s0(j),si(j)]为S0和Si在特征向量的第j个特征上的关联系数，

Gs[s0(j),si(j)]=

(4)

式中：ζ∈[0,1]为分辨率系数，一般采用ζ=0.5；wj是特征向量的第j个特征的权值，一般CBR中采用平均权值法获得每个特征的权量。

最后，通过灰色关联相似度计算得到相似的案例，选择相似度最大的前m种情况的结果，最终钢水终点温度按公式(5)计算：

(5)

式中：Gi为m种情况下案例i的相似度；Ti为这些情况下案例i钢水终点真实温度。

1.2 用粒子群优化后的案例推理方法

在一般案例推理方法的基础上，基于粒子群优化的案例推理方法被设计用于优化属性的选择和权重。

1.2.1 粒子群优化案例推理方法的计算过程

基于一般CBR的实现过程，对案例检索进行如下改进：

(1)属性约简：基于实际数据，采用多元线性回归方法对复杂的因素进行线性回归。回归系数的绝对值越大，其权值也就越高。本文在预测RH钢水终温时，保留了回归系数大于0.1的影响因素。

(2)权重优化：将一般案例推理方法与粒子群算法相结合，对保留属性的权重进行优化，目标是多个区间的整体预测精度最高。

(3)相似度计算：基于约简属性和优化权重，通过前面的灰色相似度计算出历史事件与待解决事件之间的相似度，选择相似度最高的事件作为检索结果。其过程如图2所示。

图2 粒子群优化案例推理方法的实现过程

1.2.2 粒子群优化案例推理方法中粒子群优化算法的实现

在基于案例推理的应用中，案例检索结果的准确性在很大程度上取决于相似度计算方法中属性权重的确定方法，但目前尚无可靠的属性权重确定方法。常见方法存在两个缺点：一是独立于具体问题，依赖于数理统计；另一个原因是，该方法受人类经验支配，不能保证客观性。为了得到更准确的结果，本文提出以具体问题为导向，利用粒子群优化算法确定案例推理方法中属性的权重。

1.3 粒子群算法简介

粒子群算法(particle swam optimization，PSO)是由美国的Kennedy和Eberhart在1995年提出的一种仿生优化算法。由于粒子群算法有着各种优点，包括参数少、收敛速度快、易于实现等吸引了众多研究人员的关注。它已迅速发展并广泛应用于人工智能，神经网络，控制论，函数优化等领域。

粒子群算法的流程图如图3所示。

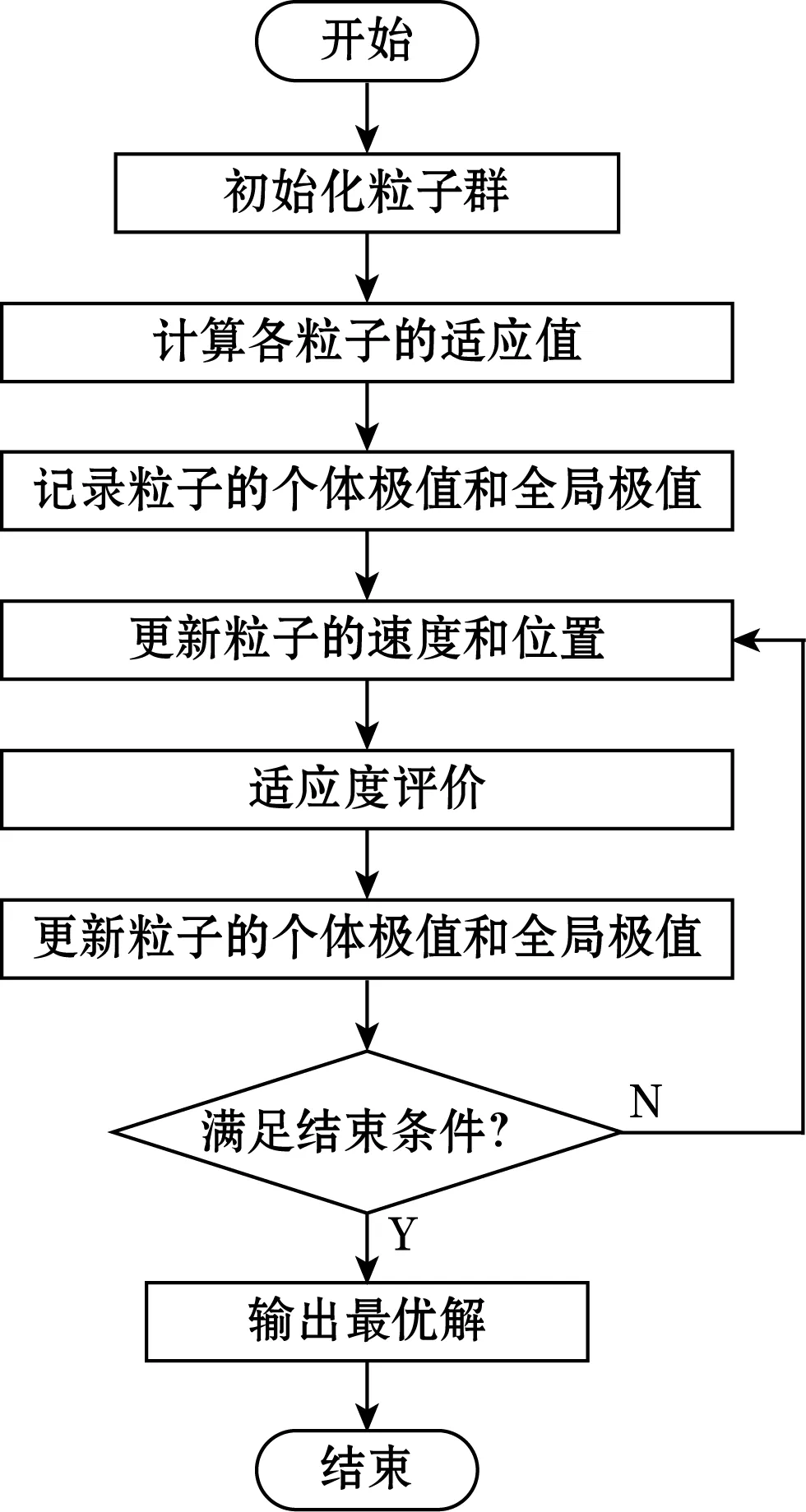
图3 粒子群算法流程图

PSO算法是源于鸟类觅食的现象，在有食物的地区，鸟类随机分布在这个区域。因为鸟群不知道食物的确切位置，找到食物的最简单方法是在距离食物最近的视线范围内寻找鸟类，最终进行整个鸟群的觅食活动。粒子群优化算法正是基于上述模型，能方便解决最优解问题，算法将鸟群中的每一只鸟抽象为搜索区域里的粒子，小鸟的航速和当前位置可以看作是粒子的速度和位置矢量，根据每个粒子自身的飞行信息以及整个粒子群的飞行信息来确定飞行的方向和距离，从而接近全局最优解。

2 系统模型的建立

建立数据库存储相关数据，分析后对温度算法进行实时更新。因此，可以通过输入(调用)钢水初始温度、添加脱氧剂量、到站氧含量、添加合金量、加工时间等来预测钢水的温度趋势，并使用RH炉的计算方程。

温度预测模型的基本方法是通过输入一级机部分的数据计算出最终钢温。由于连接了二次通讯接口，理论上可以根据站内钢水的情况模拟RH炉的精炼效果。

2.1 影响因子筛选

在整个RH冶炼中，可以认为在整个钢包中，钢水的温度平均分布在里面。在RH冶炼期间，会发生各种物理或化学变化，都会对钢温产生干扰，故需综合考虑多种因素。操作因素和非操作因素影响实际生产过程中钢水终点的温度，操作因素是指精炼过程需要采取的工艺操作，包括氩气消耗、真空室烘烤温度、总处理时间、到站钢水温度、处理开始钢水温度、加脱氧剂量、到站含氧量、吹氧量、加合金量等。非操作因素是指不可控因素，例如钢包状况以及真空室中钢水的导热和散射热等。各影响因素数据统计分析结果如表1所示，所有的影响因素都作为案例推理方法的案例属性。

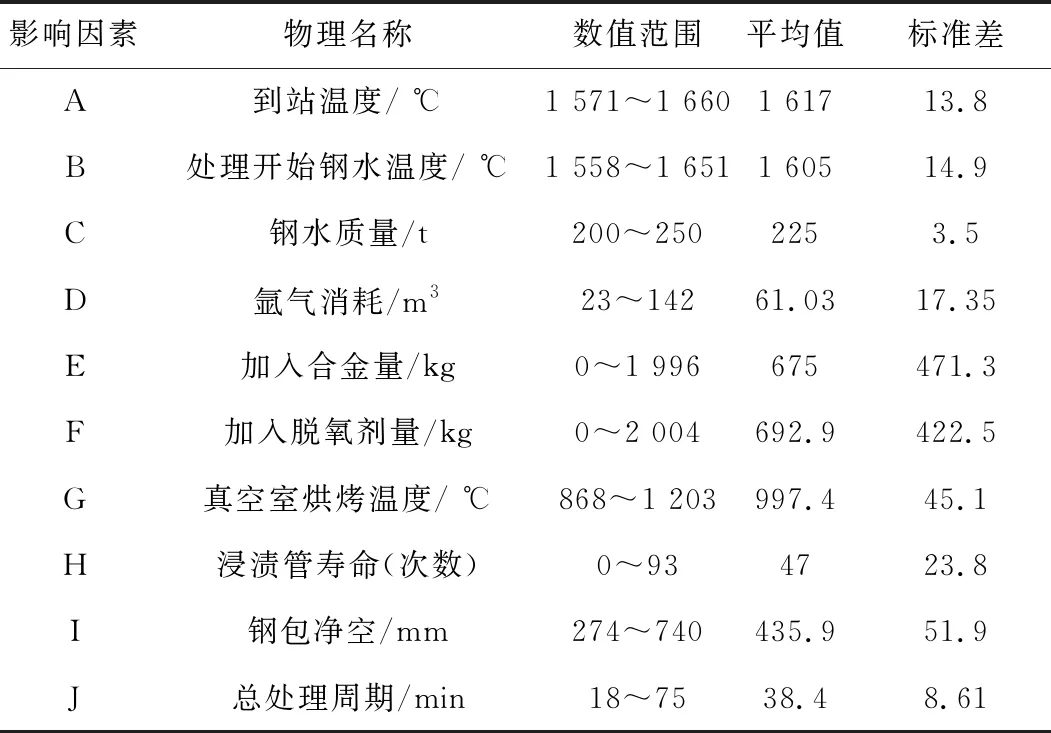
表1 RH精炼钢水终点温度的影响因素数据统计结果

对案例库数据进行多元线性回归，得到如表2所示结果。

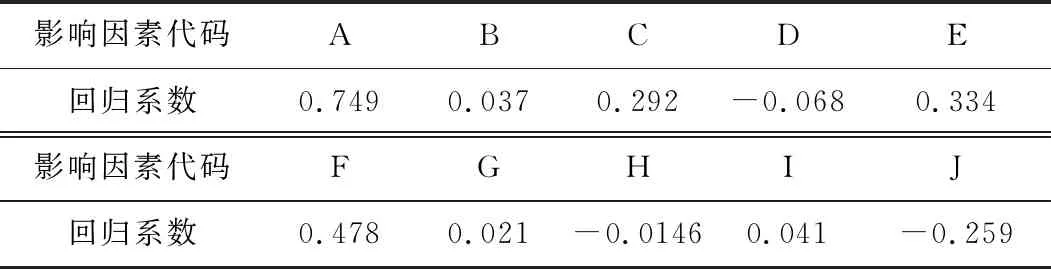
表2 各种影响因素的多元线性回归系数

为了提高案例推理方法的预测精度，采用多元线性回归方法对属性进行约简，并采用粒子群优化方法对属性权重进行优化。根据表2中的线性回归系数，保留回归系数大于0.1的影响因素，代码分别是A、C、E、F、J。

基于上述因素，预测温度可以表示为：

T预报=T0-ΔT

(8)

ΔT=ΔT1+ΔT2-ΔT3+ΔT4-ΔT5

(9)

式中：T0为到站钢液温度，℃；ΔT为过程温降，℃；ΔT1为与时间有关的温降，℃；ΔT2为加入铁合金造成的温降，℃；ΔT3为由于脱氧产生的温升，℃；ΔT4为其它因素造成的温降，℃；ΔT5为吹氧升温， ℃。

2.2 影响因子分析

2.2.1 自然温降造成的影响

受周围环境影响造成的温度变化最难预料，这是由于在生产过程中，钢水会附着在炉壁上结节。另外，真空炉内的各个部件对钢水有着温度互换的过程，且该过程不易统计处理。本文对现场数据的统计分析表明，真空室引起的温降主要与时间有关，即钢包的热损失与处理时间成正比，随着时间的增长，钢水温度减少的越多，可总结如下表达式：

ΔT1=K1×t处理时间

(10)

式中：K1为自然温降系数，℃·min-1，与吹氩流量有关，一般为1～1.2 ℃/min；t处理时间为RH处理时间，min。

2.2.2 加入合金对温度造成的影响

为了在RH处理期间达到钢液组合物的标准，应在碳氧剔除干净后进行合金化。加入的合金有一部分不参与脱氧，主要用于调整钢水中相关成分，为简化分析过程，将该合金看成能吸收热量的冷材料，投入钢炉中，产生的温度变化与添加的合金量成比例。然而，铝既是脱氧剂又是组成元素。在计算合金化温度下降时，将不加考虑地单独计算用于脱氧的铝。合金加入温降表达式为：

ΔT2=∑(Wi×K2i)

(11)

式中：Wi为合金的加入量，kg；K2i为合金温降系数，℃ · t-1，各合金温降系数如表3所示。

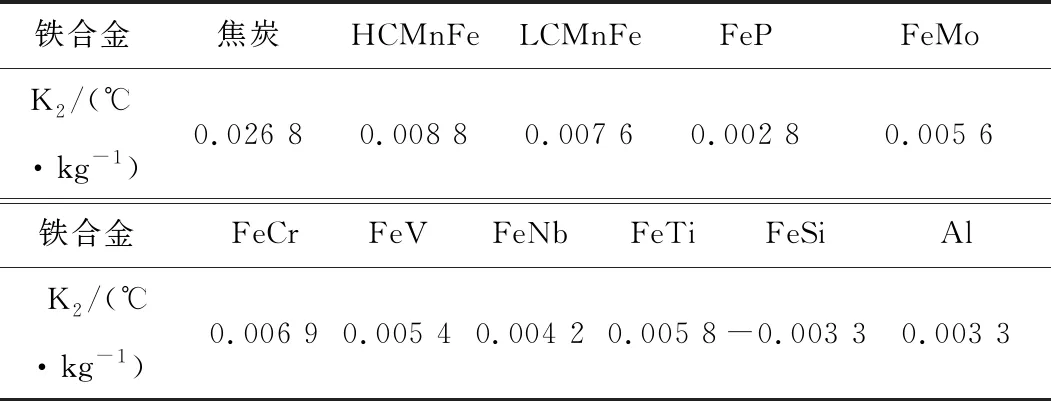
表3 各合金温降系数表

2.2.3 脱氧对温降造成的影响

在完成真空脱碳后，下一步是除去游离氧。生产工艺中一般采用铝来去除钢液中的氧，该过程会产生大量的热。铝脱氧反应方程如下：

2[Al]+3[O]=(Al2O3)
ΔH=-1218.799 kJ/mol

(12)

则脱氧升温可以表示为：

(13)

简化上式

ΔT3=[O]终点×K3

(14)

式中：[O]终点为钢水游离氧含量；K3为脱氧造成的温度变化，℃；铝脱氧K3值为3.5 ℃/100 ppm(1ppm=10-6)、其他K3值为2.5 ℃/100 ppm。

2.2.4 其他因素造成的影响

生产热处理中，罐的状态影响主要体现在蓄热和散热上。根据生产标准，由于烘烤和使用条件的不同，不同罐况的温度条件不同，因此罐况的条件是分级的。 A，B和C标志用于不同的罐况条件，并且有不同的温度下降，温降表达式为：

ΔT4=K4×t处理时间

(15)

式中：K4为钢包温降系数，℃·min-1，与罐况条件有关，钢包温降系数如表4所示；t处理时间为RH处理时间，min。

表4 各钢包温降系数表

2.2.5 吹氧对温度的影响

随着时间推移，温度会不断下降，一旦超过设定的阈值时，需要对其加热，即将氧气吹入钢水中以释放大量热量，并使热量与铝反应以加热钢水。吹氧和加铝所放出的热量由式(12)、式(16)计算。事实上，吹入的氧气并非全部参与反应，并且一些作为废气被耗尽，这需要考虑吹氧效率，根据钢厂现场实践，吹氧效率为70%。

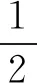
(16)

从以上分析可知，吹氧和添加铝造成的影响为：

ΔT5=6.4×VO2/W钢水

(17)

式中VO2为吹氧量，m3。

3 实验结果与分析

3.1 实验结果

通过某钢厂的生产数据，离线验证了模型的计算结果。收集310组热生产数据，其中200组作为操作指导模型和预处理的案例库数据，110组作为测试数据。为了比较不同方法的预测精度，基于该数据采用多元线性回归、BP神经网络和一般案例推理方法分别对RH钢水终点温度进行预测。

用参考文献[3]中多元线性回归模型，以终点温度为因变量，以初始温度、处理时间、加入合金量、含氧量、加脱氧剂量为自变量，建立Y=b0+b1X1+b2X2+b3X3+b4X4+b5X5模型，输出集相关性如图4所示。

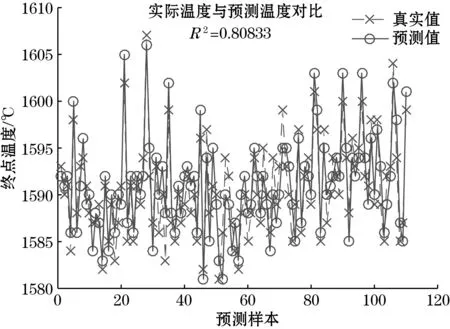
图4 基于多元线性回归的钢水终点温度预测结果

使用Matlab语言编程实现BP神经网络的计算过程[4]，包括输入层、隐藏层和输出层，其中输入层有15个节点，隐藏层有5个节点，输出层有1个节点，最大训练次数为500次，输出集相关性如图5所示。

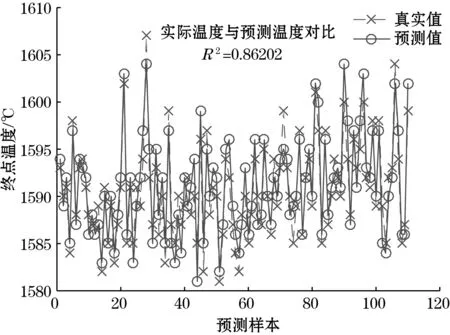
图5 基于BP神经网络的钢水终点温度预测结果

使用Matlab语言编程实现案例推理计算过程[5]，根据2.1节所述方法，将数据进行0-1归一化处理后，再采用改进的灰色关联相似度，其中的属性权值使用平均权值，输出集相关性如图6所示。

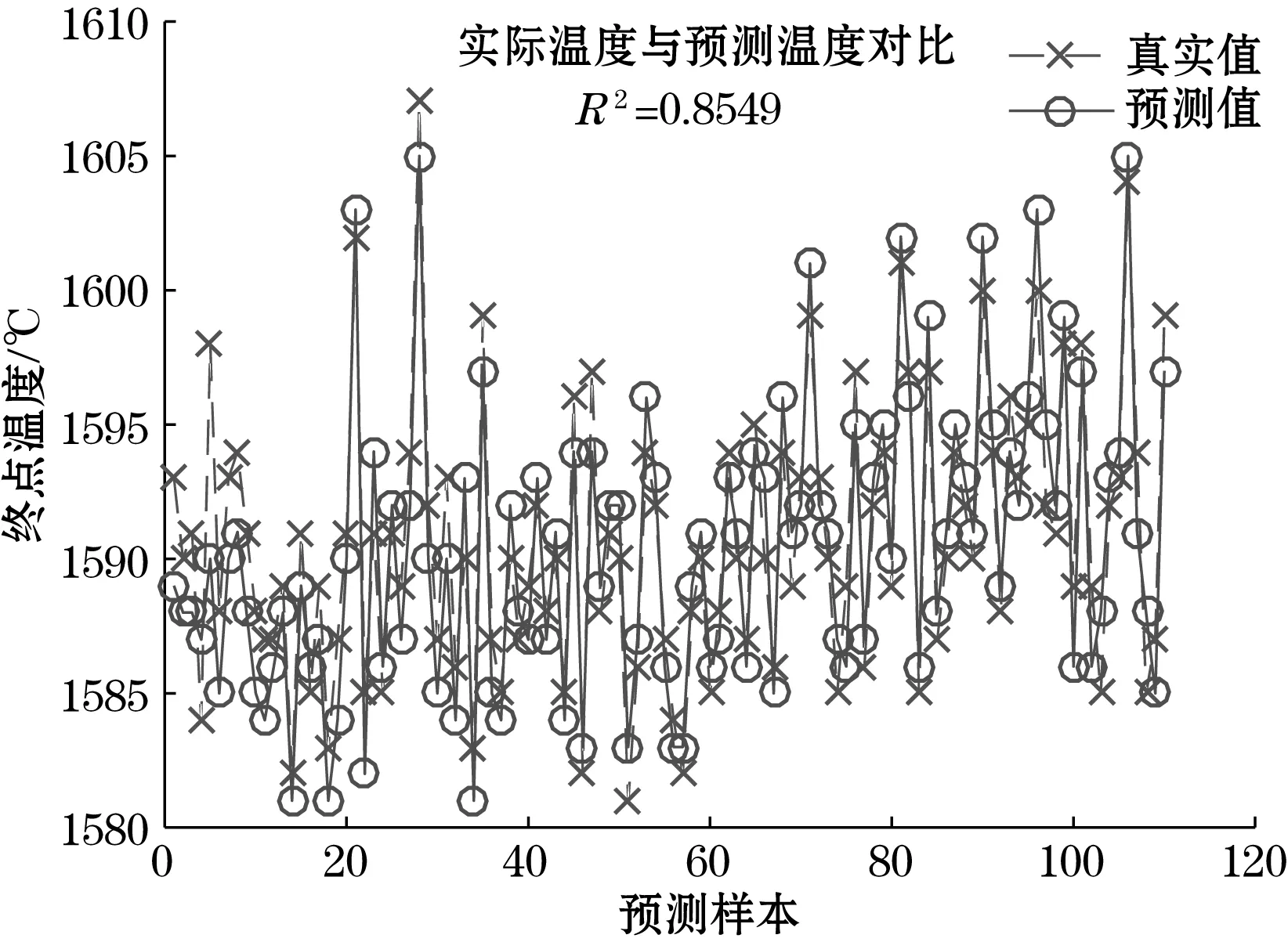
图6 基于一般案例推理的钢水终点温度预测结果

根据本文2.2.1节所介绍算法的实现过程，对属性权重进行优化。首先，将RH精炼钢端温度的影响因素的权重作为变量并满足约束条件：所有因素的权重之和为1；任意一个因素的权重大于0。

最后，通过MATLAB实现PSO优化算法和案例推理计算过程，所需参数设置如下：学习因子c1=c2=2，粒子群体个数N=40，最大迭代次数maxgeneration=100。该计算过程的演化曲线如图7所示。通过优化计算得到的权系数为[0.046 8，0.287 9，0.283 9，0.144 0，0.237 4]。

图7 PSO优化适应度变化曲线

基于约简的属性和优化的权重，利用灰色关联相似算法对RH精炼钢水终点温度进行预测，预测精度如图8所示。

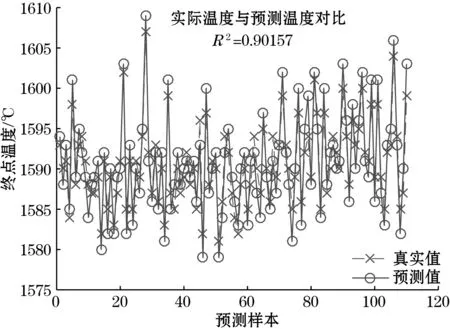
图8 基于PSO优化案例推理的钢水终点温度预测结果

3.2 分析

预测结果汇总如表5所示，表中可以看出，基于粒子群优化案例推理的准确率比多元线性回归高9.32%，比BP神经网络的准确率高3.95%，比一般案例推理的准确率高4.67%。从以上实验可以看出，基于粒子群算法优化属性权重的案例推理能够有效提高预测精度，高于一般基于事例推理和BP神经网络等方法，为RH过程的精确控制提供了有力的支持。