指数幂运算性质是怎样得出的

高田田 陈豫眉

数系扩充的核心问题是定义运算的法则和性质，其基本原则是确保原有的运算法则及其性质仍然适用于新的数集.虽然教材中给出了指数幂运算的性质，但并没有给出严格证明.下面，笔者对指数为整数、有理数、无理数的指数幂运算性质进行证明.

一、整数指数幂

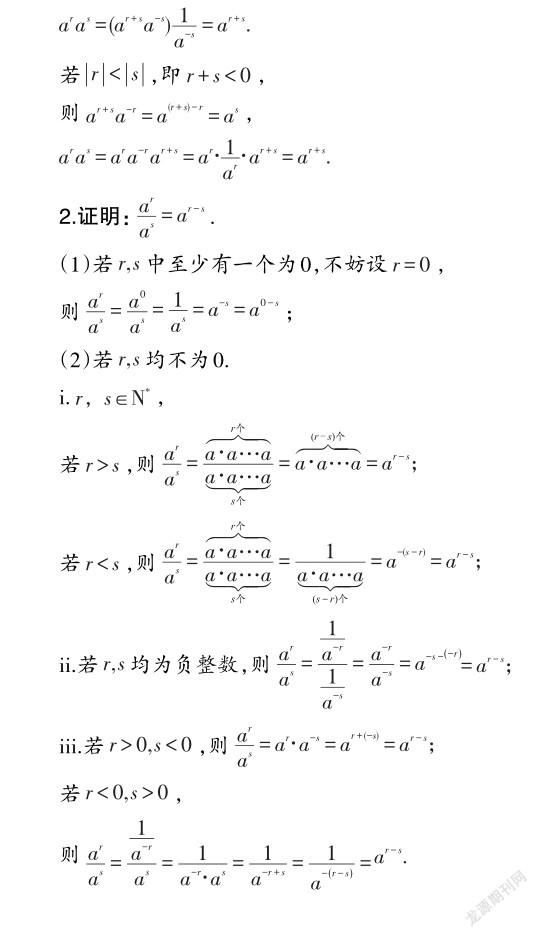
逆用指数幂的运算性质解题，要通过指数的运算推理出幂的运算.当指数做加减法运算时，幂做乘除法运算；当指数作乘法运算时，幂作乘方运算.

进行指数幂的运算很容易出现错误，同学们要识别清楚指数幂的底数、指数是否相同，明晰各种指数幂运算性质之间的区别和联系，然后合理运用指数幂的运算性质来进行求解.

同底数幂运算性质的区别与联系如上表.

我们对于指数幂的研究，并不仅限于对指数的范围的扩充，更要明確指数幂的意义及其运算的性质.在对指数为实数的指数幂运算性质进行证明的过程中，同学们不仅能充分体会到数学的严谨性，还可以感受到数学思想方法的一致性和逻辑的连贯性.

（作者单位：西华师范大学数学与信息学院）