前后悬架刚度比值及车辆行驶速度对乘坐舒适性影响的研究
2021-02-24陈子禺吾泽胤蒋佳辰李培庆
陈子禺 吾泽胤 蒋佳辰 李培庆
(1.杭州容大智造科技有限公司,杭州 310000;2.浙江科技学院机械与能源工程学院,杭州 310000)
0 引言
随着汽车工业的高速发展,进一步提升车辆动力学各个参数性能已成为研究车辆各项行驶指标的重点要求及重要组成部分[1-2]。而主动悬架系统的设计与研究更是成为车辆电气化、智能化的主要指标,研究悬架可以直接或间接的影响车辆的行驶安全性和操作安全性以及乘坐舒适性[3-4]。
而目前对于乘坐舒适性的研究主要集中在对车辆悬架系统特性的研究上。国外学者AMA Soliman 采用阻尼可调悬架的四自由度1/2 车辆模型,通过可调阻尼悬架降低车辆的垂向加权加速度均方根值,提高汽车行驶平顺性,但未分析阻尼对汽车速度的影响[5]。
?
国内研究人员李飞等人通过分析路面激励参数、悬架系统参数、悬架系统响应三者之间的耦合关系,设计了悬架系统线性化模型和有效映射悬架系统响应特性的模型[6]。王文飞等人通过对粗糙水泥路面下不同车型乘坐性能的主客观分析,识别主观及客观差异点;从路面激励传递路径出发,分析簧上、簧下振动量,提出了一种调整悬架前后偏频比的优化乘坐舒适性方法[7]。杨万安等人提出了基于PBRI 进行乘坐舒适性控制时在路径规划、车道选择、道内调整和车速控制四个不同层级下的应用策略,并展望了相应的个性化定制和应用场景[8]。刘伟等人设计了一种基于改进遗传算法NSGA-Ⅱ的悬架系统多目标优化策略,从而在改善汽车行驶平顺性的同时兼顾操作性[9]。李小龙等人通过对某段路面的研究得出一种平顺性预测模型,该模型通过平顺性预测打分与台架主观评估打分进行对比和一致性分析得出[10]。利用MATLAB和Simulink 模块建立汽车主、被动悬架模型,对车辆悬架系统进行动力学仿真,研究车辆行驶稳定性和乘坐舒适性[11-12]。还有一少部分学者致力于研究汽车座椅对于乘员的影响,对不同类型驾驶员的体压数据进行了统计分析或者是对座椅尺寸参数、结构及材料三个方面进行的探讨与演技[13-15]。
上述研究成果对于进一步研究车辆行驶平顺性有着较大的理论基础支持,但较少的学者与研究人员从车辆动力学参数着手研究分析,通过悬架上给定参数指标动力学响应特征的变化来研究悬架上参数对于车辆行驶稳定性的影响,并通过调节各参数的优化方案,进一步提升汽车乘坐舒适性。
1 道路及车辆模型的建立
1.1 道路模型
由于车辆模拟所研究的路况为一般道路上的振动规律,故采用路面功率谱密度Gq(n)作为仿真分析的系统输入。
国际化标准组织在文件ISO/TC108/SC2N67 中提出的《路面不平度表示方法草案》和国家标准GB7031 中都建议路面功率谱密度Gq(n)用下式作为拟合表达式:
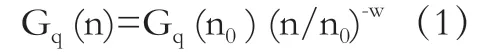
式中,n 为空间频率,m-1,为其波长λ 的倒数,表示每米长度中包含的波长数;n0为参考空间频率,m-1,一般取n0=0.1m-1;Gq(n0)为路面不平度系数,m3,表示参考空间频率n0下路面谱值,w 为频率指数,是双对数坐标上斜线的斜率,通常取ω=2。
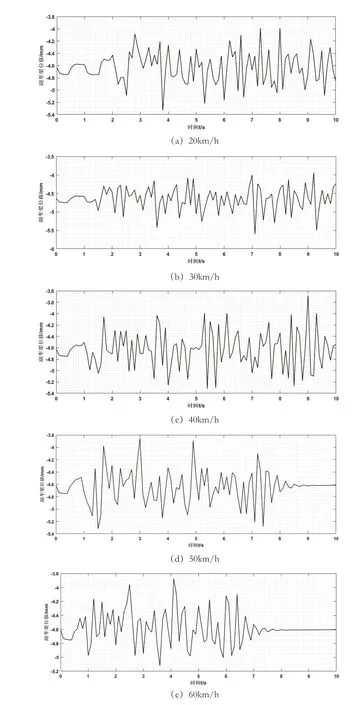
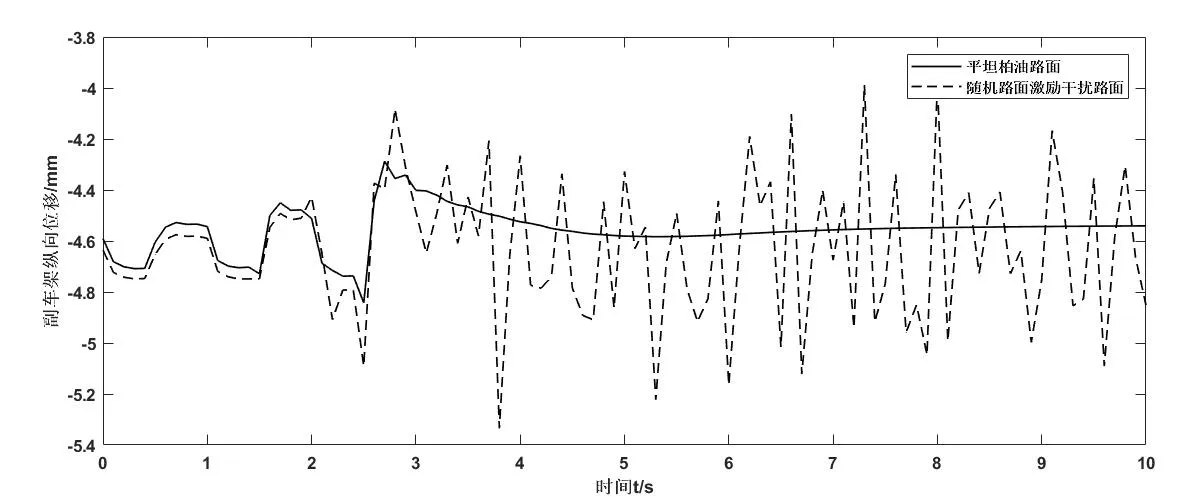
由于根据路面不平度分级标准如表1 所示,可把路面分成八个等级,其中还包括各级路面不平度系数Gq(n0)的范围以及0.011 m-1 函数Gq(n)描述路面的统计特性,仅与路面距离和表面不平度有关,与车速无关。所以为了便于分析,通常把空间谱密度函数转换为时间频谱函数,设车速为v,则空间和时间谱之间的转换关系为: 式中,f 为时间频率,Hz。 将(1)式代入(2)中可得: 当ω=2 时,式(3)可以表示为: 同样可得到时间频域内的路面不平度垂直速度和加速度的谱密度公式为: 当前我国事业单位的会计核算方法无法满足事业单位经费管控的需求。由于我国事业单位的自身特点和性质,管理者及相关人员对事业单位的会计核算重视不足,目前的会计核算方法只是用于简单的核算和记录,对财务数据的分析和运用能力不足,间接使得事业单位整体的财务信息得不到及时、全面、有效的反映。整个会计核算体系不健全,会计工作相对滞后,与事业单位发展之间要求的矛盾愈发增大。 随即将所得谱密度公式输入Adams/car 中 的road build 模 块 中,从而生成路面不平度激励。所形成模拟道路如图1 所示,该条道路将用于车辆的动力学仿真,目的时模拟随机道路所产生的激励。 图1 道路模型 在测试和优化时应用二分之一车辆振动模型,如图所使用模型将车辆的车身设为一个刚性杆,杆的质量为m,表示全车身质量的前半部分质量或后半部分质量。其纵向质量惯性矩为Ix,是车身质量惯性矩的一半。左车轮和右车轮质量分别为m1和m2(两质量通常相等)。轮胎刚度用参数kt表示,轮胎的阻尼比减振器的阻尼小得多,所以,为了方便计算,可以忽略轮胎阻尼。车辆的左、右车轮悬架通常是对称的,所以两侧的阻尼和刚度均相等,设阻尼为c,刚度为k。但对于二分之一车辆模型,车辆的前部的k、c 和kt和后部的k、c 和kt并不相同。 图2 二分之一车辆振动模型 对于前部或者后部装有扭转刚度为kR的防侧倾杆车辆,采用简单的模型,防侧倾杆的扭矩MR与侧倾角φ 成正比。 应用拉格朗日方法求二分之一车辆振动模型的运动方程为: 其中K 和V 为系统的动能和势能,其分别为: 从上式运动方程可得: 由此可得车辆动力学模型运动方程式,将该方程输入进Adams/car中的车辆模型中得到整车模型如图所示。车辆其余标准参数如下表所示: ? 图3 整车模型 对于研究车辆乘坐舒适性,主要通过振动源、乘坐感觉和车辆动力学响应特性三种方向进行深入研究,本文将以车辆动力学响应特性为研究对象,对于悬架刚度进下分析,车辆振动模型如图2 所示,由于车辆所受到的激励是从路面传递到车身,并且通过悬架系统传递,故从悬架刚度着手研究。 其中n 为悬架弹簧的有效圈数,D 为悬架弹簧中心直径,F 为弹簧所受的载荷,λ 为弹簧所受载荷F 时所产生的变形量,G 为弹簧材料的切变模量,C 为弹簧的旋绕比,又被称作弹簧指数。 由上式可知悬架弹簧刚度越大,整车悬架刚度越大,必然使得驾乘舒适性变差,而由于前后车轴所受的簧上载荷不同,前后悬架的刚度也略有不同。综上所述,研究前后轴悬架刚度之比有利于调整整体悬架表现,总而有利于提高乘坐舒适性。由上式可知,可通过改变悬架弹簧的圈数n 或中心直径D 来调节悬架的刚度。 而随着车辆行驶速度的变化,在车辆遇到振动时,车辆的俯仰运动程度也随之变化,从而间接影响了乘员的乘坐舒适性,对于多数车辆来说,垂直方向和俯仰方向的运动有耦合,故可通过图2 所示的车辆振动模型进行如下分析: 由车辆模型运动方程分析可知: 由于x1、x1分别为前轮和后轮的运动坐标,故当车辆发生前后俯仰运动时,车身前后轮坐标不断发生变化,由此影响俯仰角φ 的变化,而俯仰角φ 的数值变化直接导致车身整体的变化,从而使得乘员乘坐舒适性降低。综上,将车辆行驶速度作为另一项改进指标可以更好的研究车辆行驶稳定性,即乘坐舒适性。本文将车辆行驶速度分为五个类别,即20km/h—60km/h,间隔10km/h 的速度等级进行仿真试验。 采用初始车辆模型在所设定的道路上进行模拟仿真,由于初始车辆模型前后悬架刚度已知,故前后悬架的比值为3:4。将仿真车辆参数、道路模型参数输入后进行车辆动力学仿真。 首先得到车辆在平坦柏油路面上和随机干扰路面上,车辆以20km/h速度行驶,得到车辆副车架纵向位移的仿真数据及图表如下图所示: 由图可知,车辆刚起步时有轻微的振动,在第3s 之后,车辆副车架垂向位移趋于平稳。进一步试验车速在30km—60km/h 的情况下车辆动力学响应图,均为在车辆行驶第3s 以后车辆行驶状态趋于稳定。 下一步将路面模型替换为本次试验所用模型,再以不同速度等级,即20—60km/h 进行动力学仿真实验,得到不同速度情况下车辆副车架的纵向位由上图可知,在不改变参数指标的情况下,不同的试验组所产生的副车架垂向位移曲线各不相同,且振动幅度较为明显,即五种情况下副车架位移极大值和极小值相差明显,乘坐体验较差。 图4 平坦路面和随机干扰路面下副车架垂向位移曲线图 根据前文仿真分析结果可知,改变车辆悬架刚度的前后比值,并让不同悬架参数的车辆在与之前实验相同的速度条件下进行车辆动力学仿真实验。由于试验车辆的前后悬架刚度比值为1:1,现假设前悬架刚度值不变,改变后悬架刚度以改变整车悬架前后刚度比值,故将后悬架的刚度比值改为前悬架的1.1—1.5 倍。将其换算为Adams/car所使用的参数有效圈数n 与中心直径D,进行调整参数后的模拟试验仿真。由此得到调整前后车辆的副车架纵向位移变化关系,取出每一种情况下车辆的副车架位移极值,利用MATLAB 进行函数拟合,得到副车架位移量随着前后悬架刚度比和车速两种变量变化条件下的三维曲面图。 在方案调整以后副车架的Z 向位移量减小,从而传到车身上的振动幅度减小,进而使得乘员乘坐舒适性提高。 而通过后处理得出车辆俯仰角变化情况,通过40km/h 速度条件下的车辆俯仰角度变化对比曲线图可知,俯仰角在方案调整后也有了一定的减小,车身的前后俯仰运动趋势也有了明显的改善。 通过上述仿真结果可以得出,满足整车悬架系统正常运行的情况下,适当调整前后悬架刚度比值,且调整为1:1.3-1:1.4 之间,即后悬架刚度为39N/mm-42N/mm 之间。并且在适当的速度范围内,即车辆行驶速度为30km/h 至40km/h 范围内行驶,可以有效的改善乘员的乘坐体验,进而增加乘客乘坐舒适性。 图5 试验道路上的不同车速情况下副车架纵向位移曲线图 为了不断追求更高要求的乘坐体验,提高乘坐舒适性,本文以轻型乘用轿车为例,进行了改变整车前后悬架系统刚度的比值,以及在其在不同速度条件情况下行驶的仿真实验。将所需的车辆静态参数和动态运动方程由Adams/Car 软件建立车辆仿真模型,并且通过软件内道路构建模块进行试验所需道路模型的建立,通过间接的改变后悬架刚度的值来改变前后悬架系统刚度的比值,并同时得到了各个比值条件下不同速度等级的车辆动力学响应特征,实现了多目标化的仿真试验。最后通过利用MATLAB 进行函数拟合,所得图像便于观察改变参数指标后对于车辆副车架上的位移量变化,从而得到研究中的所使用的两项指标具有影响车辆的乘坐舒适性和稳定性的作用。 该研究方法也可适用于今后汽车主动悬架的开发中,对于悬架动力学参数影响的判定指标提供一方面的理论依据,也为汽车整体乘坐舒适性研究,且主要从事研究动力学响应特征的相关内容提供了方向。该研究内容也为不断提高汽车整车乘坐体验提供了参考和借鉴。(文责自负)
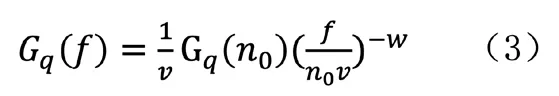
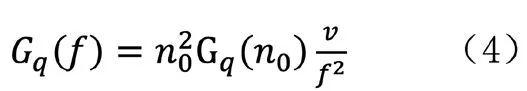
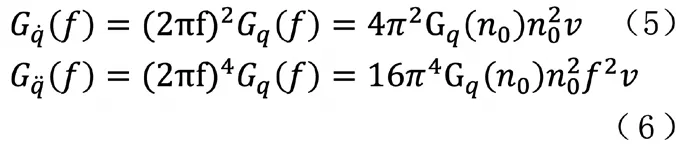

1.2 车辆模型

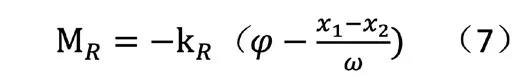
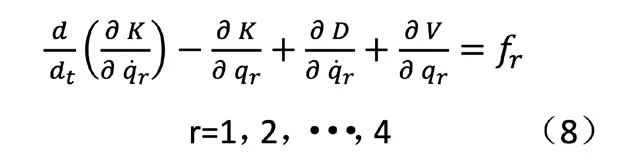
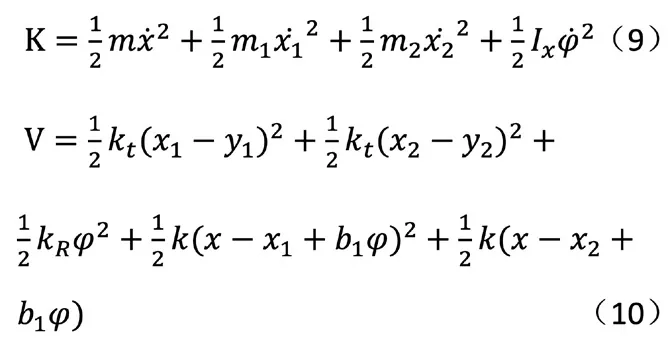
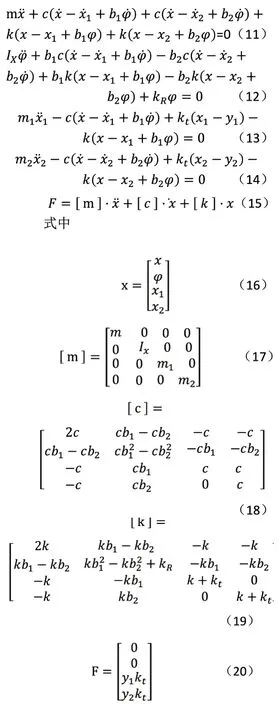
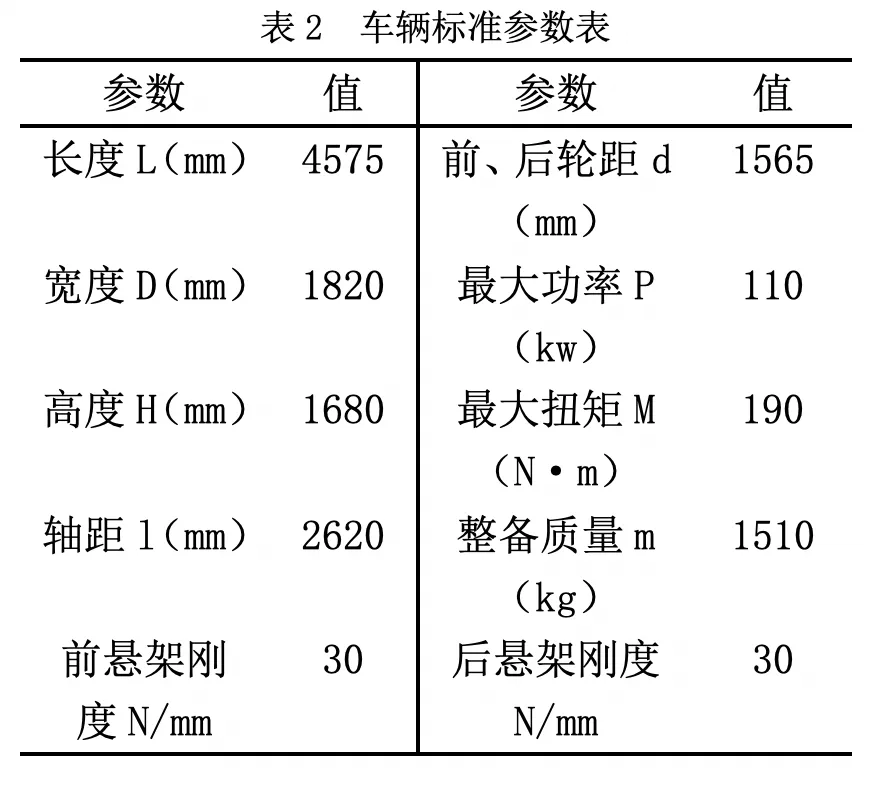
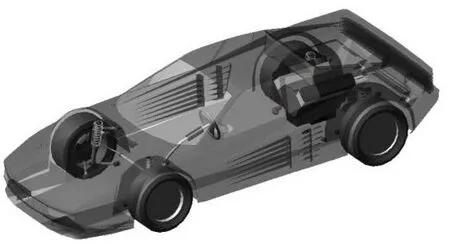
1.3 仿真分析
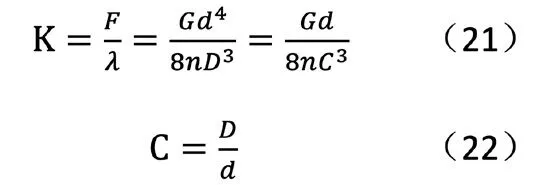
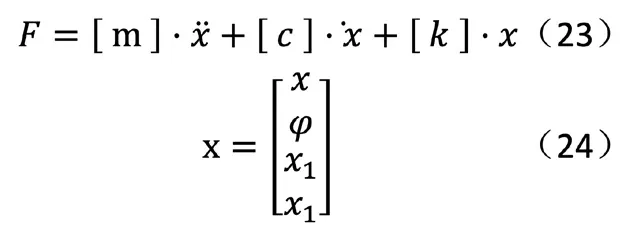
2 调整前仿真及分析
3 调整后仿真及分析
4 结果
5 结束语