500 m口径球面射电望远镜电液促动器系统空化影响的数值研究

2021-02-24秦亚璐王留根赵静一王启明

中国机械工程 2021年2期

关键词：齿轮泵电液空化

秦亚璐蔡伟王留根雷政赵静一王启明

1. 燕山大学机械工程学院，秦皇岛，066004

2. 中国科学院国家天文台，北京，100101

3. 秦皇岛燕大一华机电工程技术研究院有限公司，秦皇岛，066004

0 引言

500 m口径球面射电望远镜(five-hundred-meter aperture spherical radio telescope，FAST)是我国建成的世界上口径最大、灵敏度最高的具有主动反射面的单口径球面天文望远镜[1-2]，其主动反射系统是采用2225个促动器通过索节点拉动4450块反射面进行主动变位的工作方式来实现天体观测的，指向精度可达到8″。为保证其指向精度，实现FAST电液促动器可靠性增长和优化设计，需要对FAST电液促动器进行可靠性试验。FAST电液促动器数量较多，对单个促动器的噪声等级要求严格，系统噪声的可靠性试验尤为重要。

目前国内外对液压系统振动和噪声的研究主要集中于数学精确模型的建立、试验法和数值法。随着计算机技术的发展和噪声计算模型的完善，数值法被广泛应用于流体噪声的研究。闫政等[3]对系统油源的压力脉动特性进行仿真测试及试验验证，从噪声角度得出系统噪声的变化趋势和压力脉动一致的结论。浙江大学流体传动及控制国家重点实验室提出柱塞泵动态模型的建模思路，对流量脉动的测试原理进行了数学分析[4]。刘春节等[5]利用全空化模型对典型的液力机械柱塞泵进行了数值模拟。OBERAI等[6]、JIANG等[7]、WANG等[8]考虑固体结构和声源场的耦合，对流场噪声进行了仿真分析。然而，利用数值模拟分析液压系统吸油口管径和空化对液压系统噪声影响的相关研究成果报道较少。

本文建立了阀块吸油管路和FAST电液促动器中齿轮泵的仿真模型，并利用动网格技术对不同吸油管径条件下泵体内的压力脉动情况进行数值计算，获得了不同管径的吸油管路中的流场压力分布、齿轮泵内部压力脉动和空化程度随吸油口压力的变化规律，为FAST电液促动器的可靠性优化设计提供支持。

1 FAST电液促动器液压系统工作原理

1.1 FAST电液促动器液压系统

如图1所示，FAST电液促动器由步进电机1、双向齿轮泵2和其他流量阀组成，主要功能包括差动、小负载随动、保压、伸出和缩回。促动器伸出时，二通阀4.1关闭，同时二通阀4.2开启，齿轮泵转动，齿轮泵与溢流阀YL3之间管道内油液压力升高，液控单向阀5打开，促动器无杆腔在负压作用下通过二通阀4.2从油箱中完成吸油。促动器缩回时，二通阀4.1关闭，二通阀4.2开启，齿轮泵反转，高压油通过液控单向阀5进入促动器油缸有杆腔，控制促动器缩回。需要小负载随动时，齿轮泵停止转动，液控单向阀5关闭，二通阀4.1和4.2均开启，促动器有杆腔和无杆腔均和油箱相连，实现小负载随动。促动器差动时，齿轮泵反转，二通阀4.1开启，二通阀4.2关闭，促动器有杆腔和无杆腔通过二通阀4.1相通，实现差动功能。节流阀13用于防止促动器在受到拉伸时动作过快。溢流阀YL3.1为开启液控单向阀5的背压阀，YL3.2用于调节系统压力，YL3.3为安全阀。促动器与地锚铰接，另一端有杆腔根据地理位置不同分别采取不同的连接方式，地锚点距离反射单元较近时采用促动器伸出杆通过下拉索与索网节点连接，利用FAST促动器的闭环系统精确控制伸出位置，实现天体观测。

1.步进电机 2.双向齿轮泵 3.溢流阀 4.电磁换向阀 5.液控单向阀 6.单向阀 7.温度传感器 8.液压缸 9.位移传感器 10.压力传感器 11.测压口 12.油箱 13.节流阀

1.2 FAST促动器试验台

图2 FAST电液促动器试验台

在FAST正常观测时，促动器在下拉索的弹性变形产生的拉力作用下，始终处于被拉的状态。如图2所示，根据促动器工作特点，FAST电液促动器试验台主要可分为配重部分、支架部分、促动器、控制器、信号采集和输入部分，利用配重部分模拟促动器在观测过程中受到的下拉索的拉力，通过信号采集和输入部分控制促动器动作[9]。

1.3 FAST电液促动器噪声试验数据

如表1所示，现场6台电液促动器在工作时的噪声等级大多高于60 dB，且促动器回程噪声一般要高于促动器伸出过程产生的噪声。根据系统工作原理，齿轮泵在促动器伸出过程中，吸油侧的油液由有杆腔通过液控单向阀5流至齿轮泵吸油口，由于促动器始终受拉力，所以伸出过程中，流至齿轮泵吸油口的油液为高压油液，不存在吸空。促动器在回程过程中，齿轮泵主要通过单向阀DF2从油箱吸油，由于单向阀DF2需要一定的开启压力，并且油液存在一定的沿程损失，故造成吸空。试验样机在低速运行的缩回阶段出现振动噪声现象，出现故障时的跟踪曲线截图见图3。

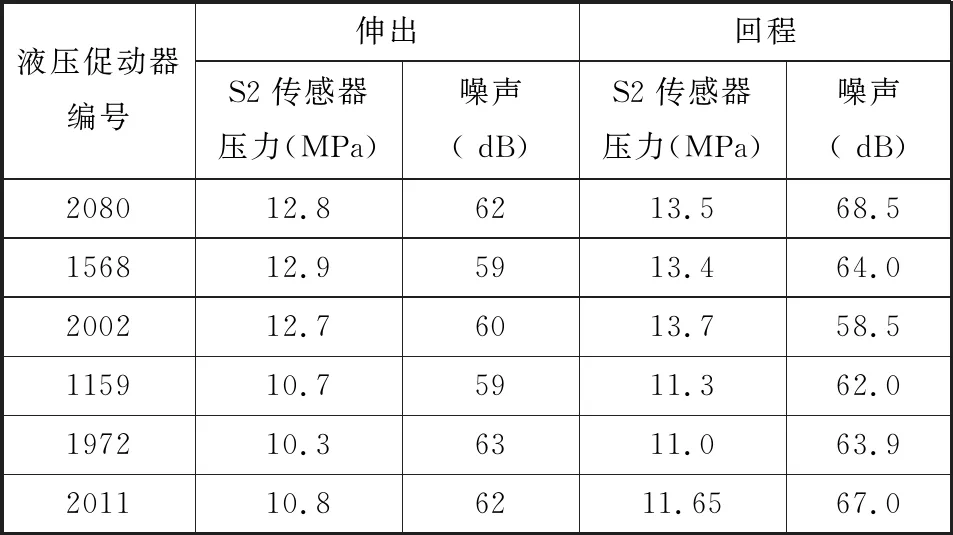
表1 电液促动器运行中的压力与噪声数据采集

2 基本理论和数学模型

液压系统空化是指流体压力低于空气分离压或者饱和蒸气压时，吸入的油液中出现气相的现象，主要发生在系统油源的吸油侧。在FAST电液促动器系统中主要产生在双向齿轮泵的吸油侧。依据亨利法则，在大气压作用下，会有部分空气溶解在油液中。溶解态的空气对油液影响较小，不会引起泵的吸空，但是当油液压力降低时，部分溶解态的空气转变为游离态或者油液中溶解的水蒸气产生大量蒸汽泡，以直径0.25～0.5 mm的气泡形式悬浮于油液中，产生空化现象[10-12]。

2.1 控制方程

空化仿真流体域内的流体应满足通用控制方程，质量守恒方程的具体形式如下：

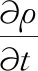
(1)

其中，ρ为油液密度；u为流体的速度矢量；Sm为连续方程的广义源项。动量守恒方程的具体形式如下：

(2)

其中，S为动量方程广义源项；μ为层流动力黏度；p为流体压力；等号左边第一项为当地加速度项，等号左边第二项为对流加速项，等号右边第一项为应力张量的散度，表示作用在单位流体体积上的表面力[13-15]。

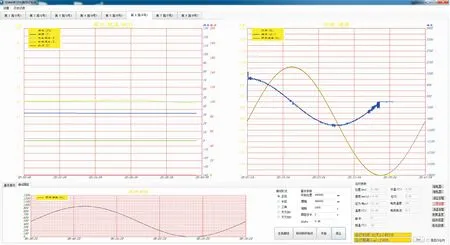
图3 出现故障现象时的截图

2.2 气穴模型

在空化过程中，流体域内为混合相，由液体和蒸汽组成，由于气泡的形成和塌缩使得液体相和蒸汽相之间发生质量转移，液体和气体之间的传质过程通过气体输运方程约束。空化模型的局限性在于流体域内的混合相只允许一种产生空化。流体的液相方程和蒸汽相方程分别为

(3)

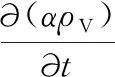
(4)

其中，α为气体体积分数；ρV为气相的密度；ρL为液相密度；uV为气相的速度；Re、Rc分别为单位时间与气泡的生长和塌缩有关的传质源项；R为净相变率，即Re-Rc。联立式(3)、式(4)混合液体方程得

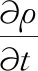
(5)

混合相密度为

ρM=αρV+(1-α)ρL

(6)

α=3nπr3/4

(7)

则净相变率为

(8)

式中，n为空泡数；r为空穴半径；pB为气泡表面压力。

3 数值模型

3.1 几何建模及网格划分

分别取FAST电液促动器阀块吸油管路部分和双向齿轮泵内部流场为流体域建立几何模型，其中，双向齿轮泵模型的主要结构参数见表2。

表2 双向齿轮泵主要结构参数

建立FAST电液促动器阀块吸油管路和双向齿轮泵的结构几何模型。由于促动器吸油管路立体分布在阀块内，如图4所示，在网格划分时采用三维网格。考虑计算网格数量和网格质量，模型采用六面体结构化网格划分[16]。

图4 阀块吸油管路三维图与齿轮泵内部装配图

促动器吸油管路模型网格数量为44 444。由于双向齿轮泵需要开启多相流和动网格设置，为提高计算效率，在网格划分时采用二维网格划分，为保证动网格计算结果收敛性，动网格区域采用三角形网格。齿轮泵最终网格数量为97 624，最终网格划分如图5所示。

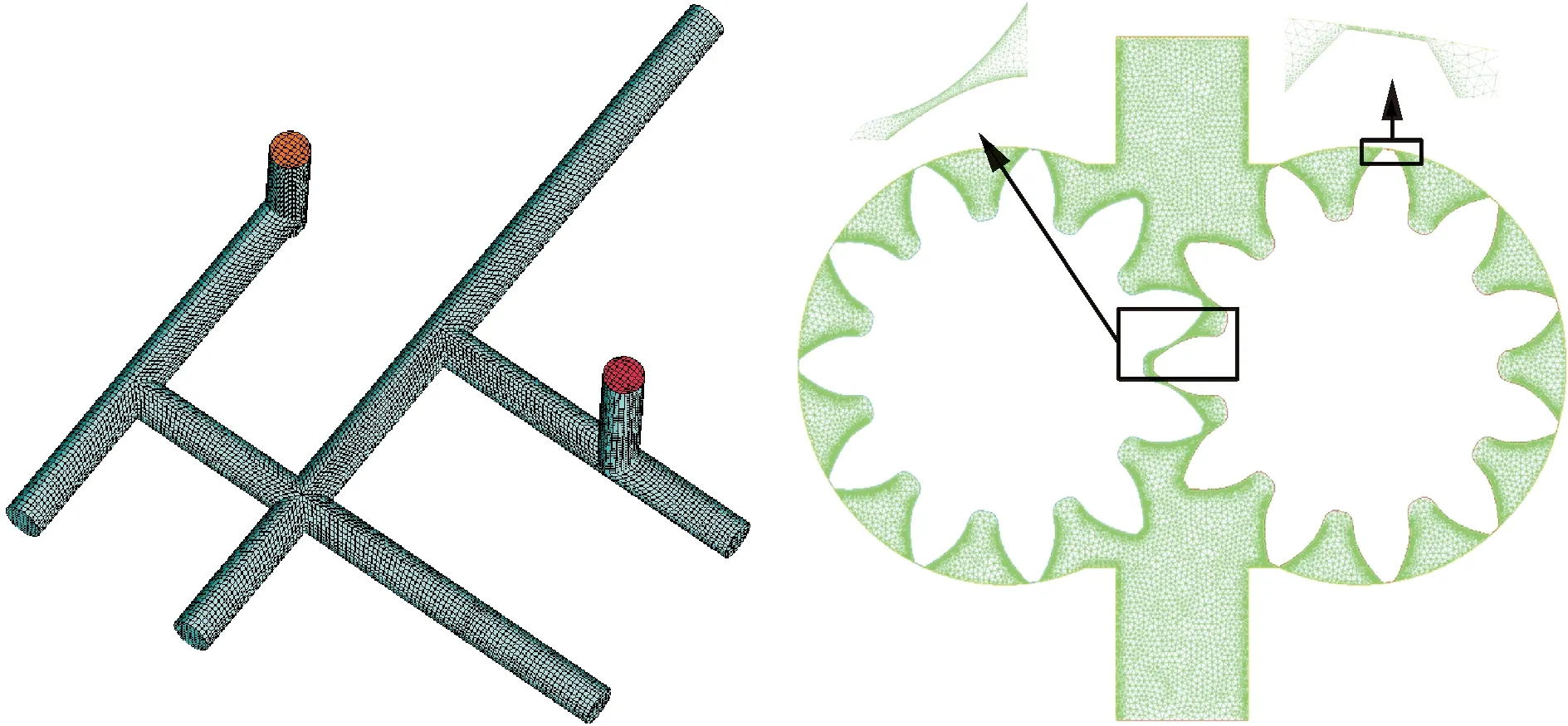
图5 FAST电液促动器阀块吸油管路和齿轮泵网格划分

齿轮泵的效率分为容积效率和机械效率两部分，仿真时主要从容积效率方面验证仿真模型的正确性，其中，容积损失主要包括齿轮端面间隙泄漏、径向间隙泄漏、齿面接触(啮合点)泄漏三个方面，在二维仿真模型中，需考虑径向间隙泄漏和齿面接触泄漏。根据相关标准，当齿轮泵中心距小于50 mm时，齿轮泵齿轮啮合侧隙安装间隙为0.085 mm，失效间隙为0.20 mm。模型中齿顶距离内壁0.02 mm，啮合间隙为0.05 mm，为避免过小间隙的存在使网格数量急剧增加，如图5所示，采用一种高度智能化的高质量网格产生软件ICEMCFD(integrated computer engineering and manufacturing code for computational fluid dynamics)对齿顶径向间隙和啮合间隙进行局部网格加密。

3.2 流动模型

在对FAST电液促动器阀块吸油管路和双向齿轮泵进行数值模拟时，湍流模型均采用标准LES模型[17]。双向齿轮泵的空化模拟采用多相流中的Mixture模型，其中油液为主相，蒸汽为次相，发生空化的为蒸汽相。

3.3 边界条件

设置吸油管路入口为压力入口，边界条件值为一个标准大气压；设定出口为质量流量出口，边界条件值根据促动器伸出时的速度设置；流体域其他边界设置为wall。系统油源设置吸油口为压力入口，边界条件值根据吸油管路出口压力设置，出口为压力出口，边界条件值根据促动器工作压力设定；设置齿轮轮廓为wall，采用UDF编程控制齿轮轮廓边界绕中心旋转，根据促动器步进电机转速设置转速。

3.4 方法验证

本文通过容积变化法计算外啮合齿轮泵理论瞬时流量，如图6所示。齿轮泵排油腔主动轮和从动轮上的齿廓由m、n、g、k、g′、n′、m′所围成，齿轮转动，齿廓mn和m′n′运动使得排油腔中的体积变小，gk和g′k使得排油腔中的体积变大。前者压缩的体积大于后者扩大的容积，从而可不断地将油液排出。根据图6，当齿轮转动Δφ角度时，则齿廓mn和m′n′运动使得排油腔缩小的体积为

(9)

式中，b为齿宽；ra为齿顶圆半径；rf为齿根圆半径；Δφ为齿轮转动角度。

图6 齿轮泵工作原理

同理，由于齿廓gk和g′k的转动，排油腔增大的体积

(10)

其中，ρ1、ρ2分别为啮合点k到主动轮圆心O1和从动轮圆心O2的距离。则可得齿轮泵理论瞬时流量表达式：

(11)

式中，ω为齿轮运转角速度。

(12)

式中，rw为节圆半径；Lpk为p点与k点之间距离。

由于是渐开线齿轮，则有

f=Lpk=rbφ

(13)

式中，φ为转角；rb为基圆半径。

将式(12)和式(13)代入式(11)，得齿轮泵理论流量qV的计算公式：

(14)

图7所示为本文数值模型仿真结果与齿轮泵瞬时理论流量曲线进行的对比结果，可以看出，齿轮泵转速为600 r/min时，齿轮泵瞬时理论仿真流量平均为0.68 L/min，仿真模型流量均值为0.62 L/min，理论值与仿真值接近，模型的容积效率为91.17%。

图7 理论流量与仿真流量对比

3.5 试验流量

根据设计的系统多元件并行可靠性试验装置方案，搭建了图8所示的试验装置，其中包括电机控制器、PLC、冷却器、液控单向阀、换向阀、溢流阀、流量计和简易伺服电机等元件。

图8 齿轮泵流量试验台

齿轮泵的试验流量数据见表3，可以看出，齿轮泵转速为600 r/min时，齿轮泵的初始容积效率平均为92.9%，加载流量平均值为0.613 L/min。

本文通过对比模型计算流量与理论计算流量和试验流量结果，验证了模型的正确性，因此，该模型能够较为准确地描述齿轮泵内部流场的瞬态数值模拟。

表3 齿轮泵试验数据记录表

4 结果与分析

4.1 吸油管流场压力分布

对不同管径下促动器阀块的吸油管路进行数值模拟，得到不同管径下吸油管路流场的压力场，原直径的吸油管压降流场图见图9。

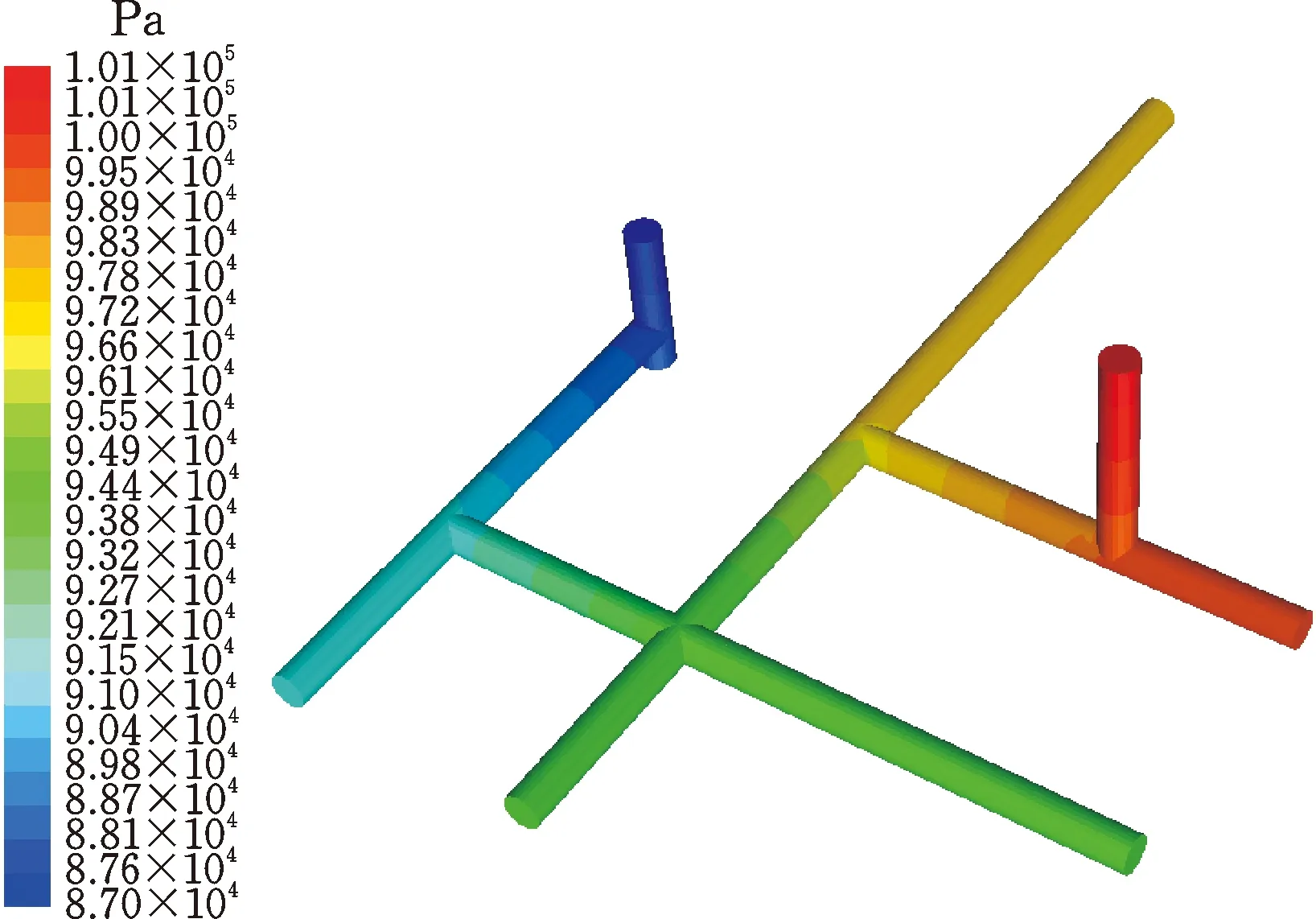
图9 原管径下吸油管流场压力

扩大吸油管直径，分析不同管径下吸油管内的压力场，得到不同管路扩大系数下吸油管内的压力场和速度场，见表4。由表4可知，随着管路扩大系数的增大，吸油管路压降逐渐减小，管路的最大流速也逐渐降低。

表4 不同管路扩大系数下的管路压降与最大速度

4.2 双向齿轮泵基本流场特征

通过对齿轮泵流场进行空化数值模拟，设置泵的吸油口压力为100 kPa，得到齿轮泵泵体内流场的气相体积分数分布随时间的变化，如图10所示。齿轮泵内流场中气相产生于齿从齿谷中退出的位置，t在0.3～0.9 ms之间，随着啮合处分离，由于齿从齿谷中退出时所产生的低压低于工作液的饱和蒸气压而形成气穴。气相中心的位置不断向吸油口运动。t=0.9 ms以后，两齿完全脱离啮合，此时低压腔的压力流场气相在进油口的压力下，对齿脱离齿谷所产生的低压区进行补充，气相所占区域体积变小颜色变浅，并最终在t=1.2 ms时几乎完全消失，此时有气相在新脱离啮合的齿面处产生。

(a) t=0.3 ms

4.3 气相变化规律

不同吸入压力下气相体积分数变化趋势计算结果如图11所示。根据表4，对比管径扩大系数从1变化到1.4时的计算结果，进出油口产生的压降降低80 kPa。

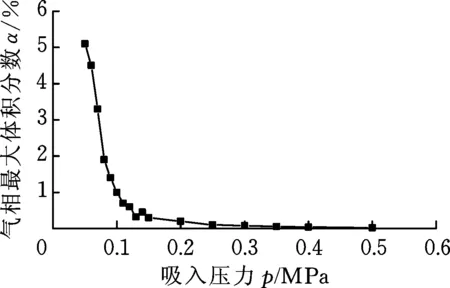
图11 不同吸入压力下最大气相体积分数变化趋势

在0～500 kPa之间分别设置不同的齿轮泵吸油口压力，转速为2000 r/min。从图11中可以看出，随着吸油侧压力的增大，流场中最大气相体积分数减小，这是因为齿从齿谷中退出时，随着齿轮的旋转，吸油腔体积突然增大，在啮合区域形成低压区。当吸油侧压力较小时，由于吸入压力不足，造成油液不能及时填充低压区，低压区的油液中溶解的气体由于低压区的压力小于空气分离压力而析出。但是随着吸入压力的继续增大，流场中最大气相体积分数减小的趋势逐渐趋于平缓但并未消失，主要原因是齿轮泵齿腔内油液在工作过程中总是经历高低压的迅速转换，而油液中气体的析出和消解这两个过程很难在一瞬间完成，所以即使吸入压力较大，流场中在齿从齿谷中退出的时候仍有空气析出。吸入压力从50 kPa变化到130 kPa的过程中，齿轮泵内部流场的气相体积分数急速减小，吸入压力大于130 kPa后气相体积分数逐渐稳定。

图12所示为不同转速下最大气相体积分数变化趋势，设置齿轮泵的转速分别为500 r/min、1000 r/min、1500 r/min、2000 r/min、2500 r/min、3000 r/min、3500 r/min、4000 r/min、4500 r/min。图13所示为转速1500 r/min与4500 r/min时气相体积分数随时间的变化趋势。

图12 不同转速下平均气相体积分数变化趋势

图13 1500 r/min和4500 r/min转速下气相瞬时体积分数

从图12中可以看出，在同一吸入压力下，随着双向齿轮泵转速从500 r/min到2000 r/min逐渐提高，流场中最大气相体积分数缓慢上升，并在2000 r/min到3500 r/min时保持稳定，转速大于3500 r/min时，气相最大体积分数又再次升高，但整体数值变化较小，说明齿轮泵的吸空主要取决于吸油口压力，当转速大于3500 r/min时，空化现象加剧。

由图13可知，气相的瞬时体积分数是随齿轮转动而周期变化的，其变化周期约等于相邻两次齿脱离齿谷的时间，在转速1500 r/min的一个出现周期内，4500 r/min大约出现了三次波峰。这和转速相差三倍相吻合。由图13可以看出，1500 r/min和4500 r/min每个周期结束时，气相体积分数接近于零，说明油液对低压区进行补充及时，气相在低压区被油液补充以后消失，但在转速大于4500 r/min的仿真试验中，出现气相虽有周期变化趋势，但在整个周期中一直存在。

4.4 压力脉动变化规律

图14所示为不同吸油侧压力下双向齿轮泵压油口监测点处的压力脉动值的频域分布。

对监测点采集到的压力脉动值进行快速傅里叶变换(fast Fourier transform,FFT)，得到压力脉动的频域分布。齿轮转速为2000 r/min时，转频为33 Hz，齿轮齿数Z=11，则齿轮泵的齿频为363 Hz，对比图14中在不同吸油侧压力下齿轮泵压力脉动的频域分布可以看出，不同的吸油口压力pin下，出油口的压力脉动主频均为齿频的二倍频即726 Hz，且随着吸油口压力的增大，主频幅值逐渐减小。当吸入压力大于130 kPa时，压力脉动变化不再增大。

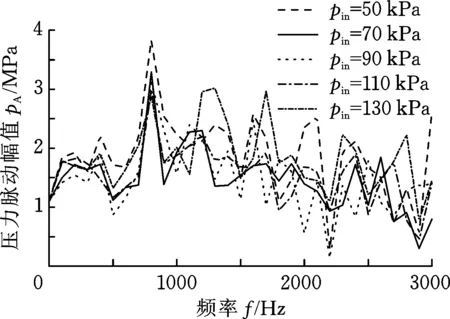
图14 不同吸油侧压力下双向齿轮泵压油口监测点处压力脉动值的频域分布

4.5 试验验证

结合图14和图11可知，系统空化程度、压力脉动值趋势保持一致，且与系统的转速和吸入压力有关。空化出现时，流场中出现气泡的成长和溃灭过程，同时气泡受到压缩和膨胀，增加流场压力脉动，进而产生更高的噪声。通过改变吸油管路直径增加齿轮泵吸入压力，进而减少系统的振动和降低噪声，图15所示为对阀块吸油管路进行扩大后的跟踪曲线。