基于磁通恒定的多相感应电动机起动过程分析

王 健，吴新振

基于磁通恒定的多相感应电动机起动过程分析

王 健，吴新振

（青岛大学电气工程学院，山东 青岛 266071）

传统的控制方式在低、中频条件下对多相感应电机进行起动时，由于定子电阻和漏感压降不能忽略，起动过程中的起动电流波动较大，致使多相感应电动机在起动过程中的稳定性能较差。本文以三套三相绕组在空间上互差p/9电角度构成的九相感应电动机为研究对象，对传统的控制方式在低、中频条件下进行了优化。基于DSP+FPGA芯片编程，采用探测线圈反馈九相感应电动机的真实电动势，通过直接控制电动势，并根据电动势与频率的比值为常数的原则，保持电机磁通恒定，以此来起动九相感应电动机。通过实验证明，采用该控制方式起动的九相感应电动机具有更好的稳定性能，优化了九相感应电动机的起动过程。

控制；九相感应电动机；探测线圈；DSP；FPGA

0 前言

与传统的三相感应电动机相比，多相感应电动机具有转矩脉动更小[1]、容错性更高[2,3]、可控的自由度更高[4]等优点，因此多相感应电动机被广泛地应用于舰船推进等领域[5]。

目前，在感应电动机的调速系统中，控制方式因无需反馈、简单易实现、节省成本等优点被广泛应用。同时，控制方式也存在诸多的问题，传统的起动方式粗略地认为定子相电压s≈g，根据定子相电压与频率的比值为常值的原则来进行起动，因其在低、中频条件下定子电阻和漏感压降不能忽略，使其在起动过程出现起动电流过大、电流振荡等问题[6]。

对于电机在空载和轻载条件下易发生的振荡问题，文献[7]详细地阐述了感应电机控制方式中引起持续振荡的诸多因素，譬如定子电阻的大小、死区时间的长短、转子电阻的大小、转动惯量的大小等，这些因素均会影响感应电机在轻载情况下的电流振荡，导致电机起动性能较差。

针对感应电机控制方式下起动过程的起动电流较大问题，文献[8]通过对电流进行解耦，提出了一种分别控制d、q轴电流的方法，该方法能够有效地降低电机的起动电流。文献[9]基于电流解耦的方法，对控制进行了死区补偿，能够有效地改善电流，在低频工作下也能达到提升转矩的效果。

本文以三套三相绕组在空间上互差p/9电角度构成的九相感应电动机为研究对象，针对其起动问题，采用控制方式对电机的起动过程进行了优化，在电机起动时，通过探测线圈对感应电动机的真实电动势进行信号的采集、处理并反馈，由Matlab上位机、DSP、FPGA对其进行算法编程，将反馈电动势信号作用于起动过程。相较于传统的控制方式，该方法能有效地解决起动电流过大问题，且该方法无需解耦，简化电机的起动算法。最终用实验证明，该起动方式相比传统的起动具有更好的稳定性能，有效地减小了电机的起动电流。

1 九相感应电机的数学模型

本文研究的九相感应电动机的转子为鼠笼结构，物理模型如图1所示。其在自然坐标系下的数学动态模型由磁链方程、电压方程、电磁转矩方程和运动方程四部分组成[10]。在研究其数学模型时，我们作如下的假设：（1）忽略空间谐波；（2）忽略磁路饱和；（3）忽略铁心损耗；（4）不考虑频率变化和温度变化的影响。

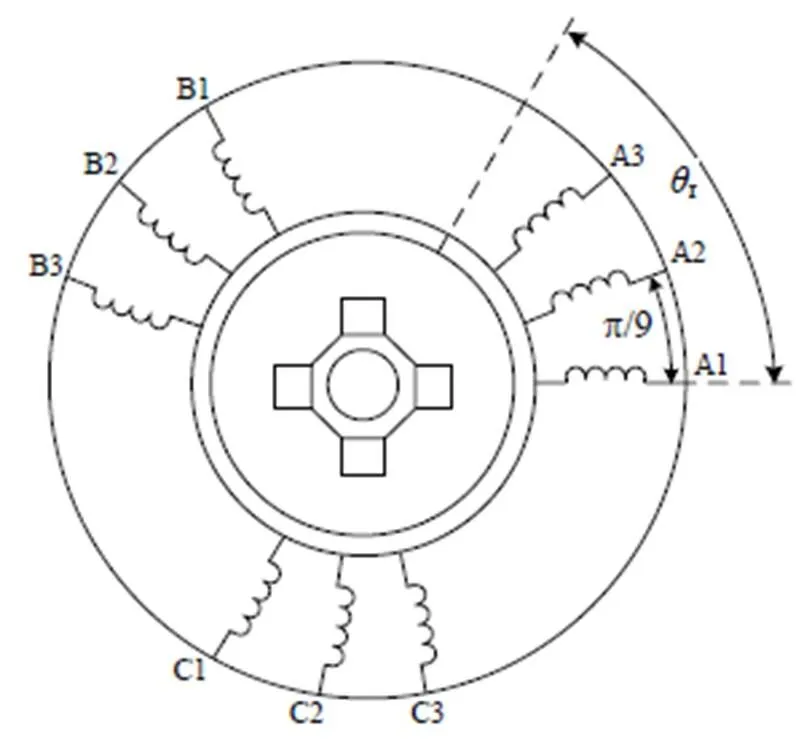
图1 九相感应电机物理模型

（1）磁链方程

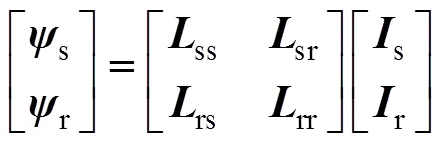
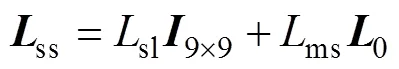
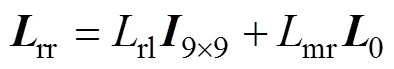
上述两式中，九阶矩阵0为：

对于定、转子的互感矩阵，则有：

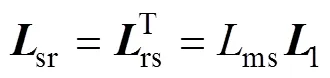
上式中，九阶矩阵1为：

（2）电压方程

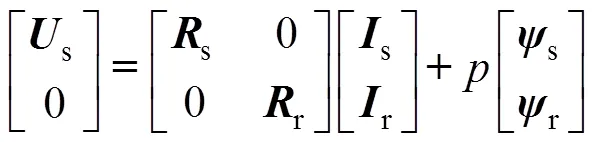
（3）电磁转矩方程

（4）运动方程

2 基本原理

2.1 传统V/f控制方式的电流不稳定问题

采用折合算法后，电机转动之后的T型等效电路如图2所示。

图2 电机转动之后的T型等效电路

根据图2可知：

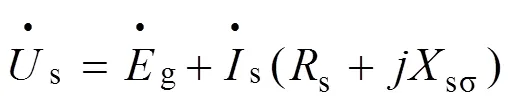
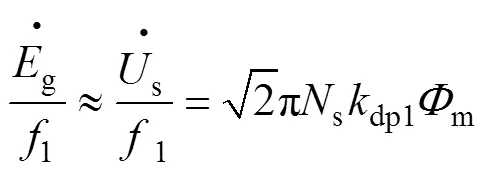
而绕组产生的总磁动势为：

其中，为电机的相数；m为励磁电流；为电机极对数；1为绕组匝数。

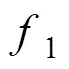
2.2 探测线圈反馈电动势

优化后的电机起动控制框图如图3所示。控制原理如下：通过Matlab上位机给定参考转速ref，在DSP中求得当前转速相对应的频率，根据额定条件下的感应电动势81.1754V与额定频率50Hz的比例关系，求得当前频率对应的理论电动势有效值*。探测线圈的输出电势与电机绕组实际感应电动势的比例系数为，得到真实感应电动势的有效值，其数值大小为t。将反馈的真实感应电动势有效值与理论电动势有效值进行比较，经过比例环节，求得实际输出电压out，最终九相变频柜在DSP+FPGA的作用下生成SPWM来控制开关管的开通、关断，为九相感应电动机提供九相交流电压，电机起动。

图3 优化后电机起动控制框图

2.3 比例系数k的计算

功率绕组上的实际感应电动势与探测线圈输出电动势的差异体现在两个变量：每相串联匝数和基波绕组系数dp1。而探测线圈是一个整距集中线圈，基波绕组系数dp1=1。对于功率绕组上的基波分布因数d1，由于各线圈是分布的，基波分布因数d1就相当于基波电动势相对于采用集中线圈（dp1=1）时应打的折扣，故基波分布因数是一个小于1的数，求得dq1=0.9577。

功率绕组上的感应电动势与探测线圈输出电动势的转换比例系数为：

其中，1为气隙每极基波磁通量；1为电机每相串联匝数；2为探测线圈绕组匝数。已知2=1/4，代入公式可得出：=3.83064。

3 仿真验证

根据上述式（1）~（9）推导得出的动态数学模型，在Matlab/Simulink平台中搭建九相感应电机模型，电机参数见表1。供给幅值为85V，相位差为p/9的九相电压，实现九相感应电机的起动。

表1 九相感应电机基本参数

根据对传统起动控制方式下的九相感应电机仿真结果进行分析，发现电机从0s时刻开始，逐渐提速，在0.6s左右达到额定转速。图4所示为九相电流中的A1相电流，电机在起动过程中的低、中频段电流较大。故传统的控制方式在起动电机时是存在一定缺陷的，为证明本文所提方法的可靠性，接下来将对传统控制方式和控制方式分别进行实验验证。

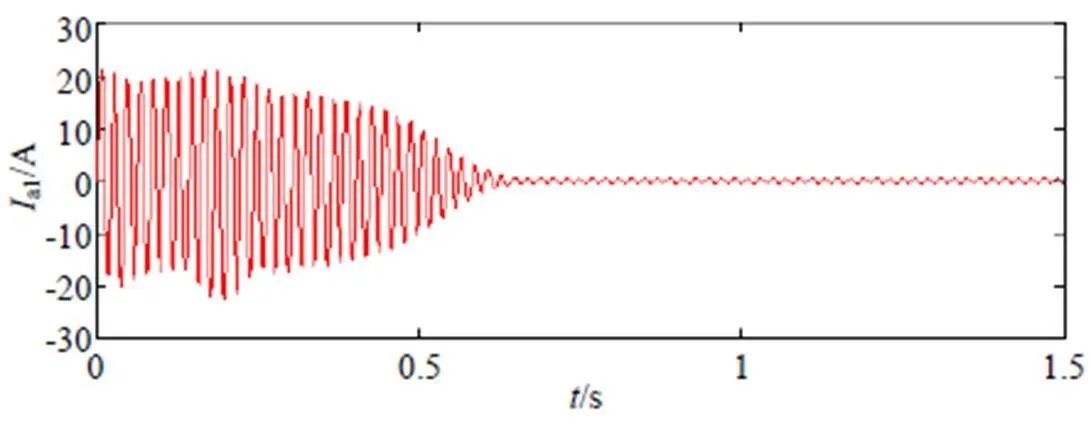
图4 A1相电流

4 实验验证

4.1 实验平台

为验证优化后的控制方式相比于传统的控制方式具有更好的稳定性能，对九相感应电动机进行空载实验，九相感应电动机如图5所示，基本参数见表1。

图5 九相感应电动机

由电网接入可调直流电源柜，直流柜发出所需额定相电压85V，并为九相变频柜供电，由Matlab输入参考转速、电压调制比、转速上升时间等参数，然后通过变频柜中的控制单元DSP+FPGA编程实现九相电流的输出，为九相感应电动机提供相位差为p/9的交流电，由录波仪记录实验波形，实现电机空载实验，电机转速通过转矩转速测量仪观测。

4.2 实验结果分析

为了增强对比性，证明优化后的控制方式起动稳定性更强，分别进行了传统的控制电机起动空载实验，以及优化后的控制电机起动空载实验，并通过录波仪记录九相感应电动机的起动过程。图6所示为探测线圈采集的九相感应电动机电动势信号，在式（14）中，已经得到了探测线圈采集的电动势与感应电机功率绕组上的电动势的比例转换关系，将其经过一个简单的软件滤波后转化为电机真实电动势反馈到控制环节，起动电机。

在传统的/起动实验和本文/起动实验中，使用电流钳对九相电流中的A1相电流a1进行观测。相较于仿真结果，实验中对转速的上升时间进行了控制，为更好的观测起动过程，实验中的起动时间会比仿真中的长。图7所示为传统的/控制方式起动九相感应电动机的过程，不难发现，采用传统的/控制方式起动九相感应电动机时，在低、中频情况下电流出现明显的不稳定状态，会产生较大的冲击电流，起动效果不理想。

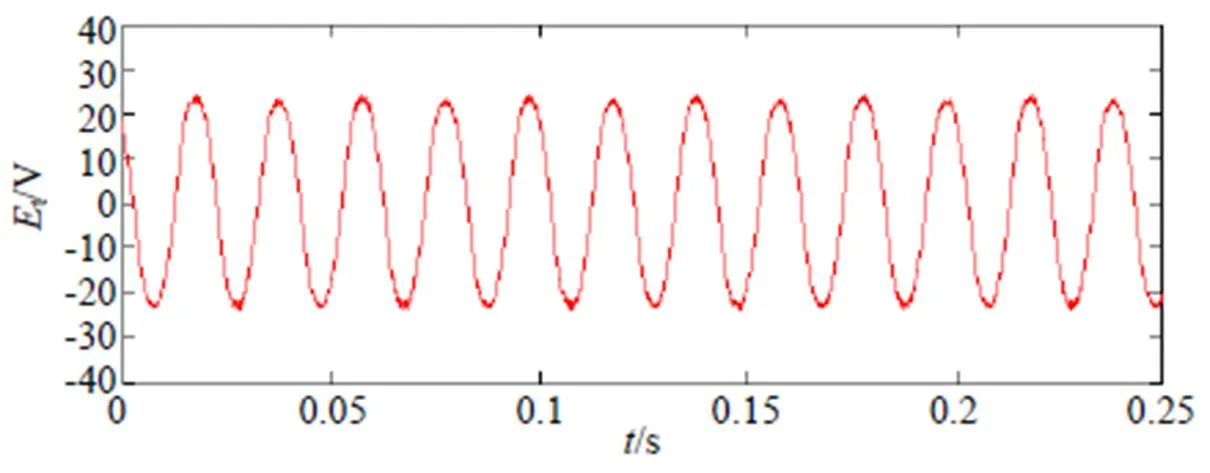
图6 额定转速时探测线圈采集的电动势

图7 传统的V/f起动电机过程

图8所示为本文提出的优化后的/控制方式起动九相感应电动机的过程。显然，相比于传统的/控制方式，在起动九相感应电动机时，优化后的控制方式具有更好的起动稳定性能，能够有效地减小冲击电流，使得电机在低、中频起动电机过程中更加平稳。

图8 优化后的E/f起动电机过程

5 结论

本文针对传统的/控制方式出现的起动电流过大问题，以九相感应电动机为研究对象，通过探测线圈反馈电机的电动势，采用了/控制方式以保持磁通恒定来起动电机，该方法无需电流解耦，控制简单。为证明其相比于传统的/控制方式具有更优异的性能，分别对/控制方式和优化后的/控制方式进行了空载实验比较，最终实验表明：经优化后的/控制方式在九相感应电动机起动的过程中，具有更稳定的起动性能，能够减小电机在起动过程中的起动电流，有效地优化了电机在低、中频条件下的起动过程。

[1]Pandit J K, Aware M V, Nemade R V, et al. Direct Torque Control Scheme for a Six-Phase Induction Motor With Reduced Torque Ripple[J]. IEEE Transactions on Power Electronics, 2016, 32(9):7118-7192.

[2]Munim W N W A, Duran M J, Che H S, et al. A Unified Analysis of the Fault Tolerance Capability in Six-Phase Induction Motor Drives[J]. IEEE Transactions on Power Electronics, 2017, 32(10):7824-7836.

[3]Liu Z, Wu J, Hao L. Coordinated and Fault-tolerant Control of Tandem Fifteen-phase Induction Motors in Ship Propulsion System[J]. IET Electric Power Applications, 2017, 12(1):91-97.

[4]Levi E. Advances in Converter Control and Innovative Exploitation of Additional Degrees of Freedom for Multiphase Machines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1):433-448.

[5]黄泽森，谢卫，杜彦清. 船用五相感应电动机的矢量控制研究[J]. 微特电机, 2019, 47(6):73-77.

[6]王天雷，张京玲，等. 异步电机V/f调速轻载振荡抑制方法研究[J]. 微特电机, 2017, 45(1):73-76.

[7]陈伟，金辛海，蔡亮，徐殿国. 异步电机V/f控制系统轻载稳定性仿真研究[J].中国电机工程学报, 2013, 33(S1):211-218.

[8]李洪亮，姜建国，周中正. 异步电机V/F控制系统起动和某频段振荡问题[J]. 电机与控制学报, 2017, 21(1):90-97.

[9]邝志坚，钟汉如. 异步电机V/F控制方法的死区补偿[J]. 工业仪表与自动化装置, 2016(5):96-99.

[10]沈佳，谢卫，屈鲁. 九相感应电动机调速系统的建模与仿真[J]. 电机与控制应用, 2015, 42(7):44-48.

Analysis of Starting Process of Multi-phase Induction Motor based on Constant Flux

WANG Jian, WU Xinzhen

(College of Electrical Engineering, Qingdao University, Qingdao 266071, China)

When the traditionalcontrol method starts a multi-phase induction motor under low and intermediate frequency conditions, the starting current during the start-up fluctuates greatly due to the stator resistance and leakage inductance voltage drop, which causes poor stability of the multi-phase induction motor during starting. This paper takes nine-phase induction motors composed of three sets of three-phase windings in spatially differentp/9 electrical angles as the research object, and optimizes the traditionalcontrol method under low and intermediate frequency conditions. Based on the DSP+FPGA chip programming, the detection coil is used to feed back the real electromotive force of the nine-phase induction motor. The nine-phase induction motor is started by directly controlling the electromotive force and according to the principle that the ratio of the electromotive force and the frequency is constant to keep the motor flux constant. It is also proved by experiments that the use of this control method to start a nine-phase induction motor has better stability and optimizes the starting process of a nine-phase induction motor.

control; nine-phase induction motor; detection coil; DSP; FPGA

TM346

A

1000-3983(2021)01-0024-05

2020-07-19

王健（1996-），青岛大学电气工程学院在读硕士研究生，研究方向为多相感应电机控制。