中子通量测量系统可靠性

孙凌宇, 李鑫宝, 刘 策, 朱丽莉, 吕晓玲

(河北工业大学机械工程学院， 天津 300131)

20世纪70年代至今，中国的核电事业已经有了四十多年的迅猛发展，已建成的核电站包括广东大亚湾核电站、江苏田湾核电站和浙江秦山核电站等大型核电站，其装机容量近1 100万kW。2007年,国务院正式批准了国家发展改革委员会上报的《国家核电发展专题规划(2005—2020年)》，根据国家政策方针的指引，中国核电站的建设步伐还会越迈越大，计划将要进行的核电工程建设将有近30个。

然而纵观中国乃至世界的核电发展历程，一旦发生事故，将会有大量放射性核素不可控地释放，导致严重甚至是毁灭性的后果，所以核电的建设和使用需要倍加慎重。近有日本的福岛核电站事故，远有乌克兰的切尔诺贝利核电站事故，不仅对核电的声誉造成了很大的负面影响，还加重了人民乃至政府对核电安全性的担忧与恐慌，在美国甚至还曾出现过反对核电建设的游行。由此可见，核电能否可靠安全的使用，是决定核电能否顺利发展的重要因素。

核电能否被安全使用受诸多因素的影响，但最重要的一点，是设法保证核电站的正常运行，准确地监测出堆芯的各种运行状态参数，为反应堆操纵员操控反应堆功率提供依据；同时一旦有事故发生，能够及时可靠地应对，防止事故的继续扩大，基于此类需求，堆芯运行状态监测仪应运而生。堆芯运行状态监测仪通过对反应堆内温度和水位的连续在线监测和分析，能够实时监测堆芯的功率分布和运行状态，而对于核电站这种十分重要且异常精密的设施，用于准确监测出堆芯的各种运行状态参数的仪器的可靠性就异常重要。而目前核电行业中，核级设备并没有完整的可靠性分析鉴定的流程和方法体系，因此对于堆芯运行状态监测仪的可靠性分析需要进一步的深入研究和完善。随着可靠性学科的发展，学者们提出了许多相关的可靠性分析方法，如张鸿等[1]针对民航发动机设计阶段可靠性数据较少的缺点，将现有可靠性计算模型进行改进，从而准确估算可靠性指标；吕文红等[2]基于大数据分析构建动态有向网络模型，论述了交通运输网络可靠性进展；雒卫廷[3]通过改进应变模态对数控机床滚动轴承可靠性检测，成功获取不同测点的检测结果，提高了检测准确率。

在以往的可靠性分析中，对于类似于堆芯测量(reactor in-core,RIC)系统这种大型电子设备，常用的分析方法有蒙特卡洛方法[4-5]、可靠性方块图(reliability block diagrams,RBD)框图法[6]、故障树分析法[7]、Markov方法[8-9]以及GO法[10-11]。而这些方法的缺陷也很明显，蒙特卡洛方法需要实现建立合理的概率模型，再基于随机数的统计模拟得到系统可靠性，它对零件失效分布没有规则，不能清晰地表明系统状态的转移情况[12]；RIC系统是一个复杂的多时序多状态机电系统，其从正常运行到完全失效的过程中呈现多个状态，而对于RBD框图法和故障树分析法等常规的可靠性分析理论中所讨论的正常状态、完全失效的二元化分析方法，不能够完全体现堆芯运行状态监测仪在运行过程中可用度等各可靠性指标的变化。在研究多状态系统可靠性分析中，Markov模型和GO图模型是常用的可靠性建模方法。Markov模型从研究系统状态的角度出发，其所建立的模型涵盖了从正常运行到完全失效之间的工作状态，并考虑了各个模块组件的状态对应了系统处于什么状态；GO图从系统的原理出发，通过研究各个模块的原理和作用，可以构建出系统的GO图模型，从模块的可靠性推广至系统的可靠性，并通过模块的失效率等数据求出系统的可靠性指标，这两种模型应用于RIC系统的可靠性分析具有显著的研究价值和意义。

因此，现综合运用Markov法和GO法，提出一种新的方法来对中子通量测量系统的硬件可靠性进行分析。最后，以预制RIC系统作为算例，对其系统的硬件可靠性进行分析。使堆芯运行状态监测仪的可靠性分析结果更加严谨且符合实际状况，同时也对提高堆芯运行状态监测仪的可靠性、安全性和各种故障的诊断等都具有重大的意义，也为类似的核级仪器[13]的可靠性分析提供依据。

1 中子通量测量系统简介

堆芯运行状态监测仪属于核级专用仪器，主要用来对核电站堆芯的中子通量、水位等参数进行实时的测量，是核反应堆安全测量不可或缺的重要仪器。该监测仪系统的主要功能包括对反应堆内的中子通量、温度和水位进行测量，其中各功能模块按照信息传送角度又可以分成信息的测量、信息的传输以及信息的处理。

整个系统分为两个部分，分别为深入压力容器内堆芯的探测传感器部分和位于压力容器外的信号处理端，传感器部分主要由中子-温度探测组件和水位探测组件组成，信号处理端压力容器外的中子信号处理机柜与水位信号处理机柜,压力容器内外环境大不相同，容器内是高温高压高辐照的环境，压力容器外是厂房环境。中子通量信号通过堆芯一体化测量组件，将传感器信号送入服务器中，再经由通讯站传入分布式系统(distributed systems,DS)中；水位信号通过相关的水位调理之后送入事故后监测系统，同时实时显示堆芯内水位和中子通量状况，给相关工作人员提供重要的数据支持。因中子监测子系统为RIC系统最重要的组成部分，故着重研究中子监测子系统的可靠性。

中子监测系统主要监测堆芯出口温度、中子通量和压力容器上封头温度。堆芯出口温度监测子系统用于监测燃料组件出口处的冷却剂温度，用于严重事故处理规程，堆芯出口温度测量仪表的量程应该满足0～1 200 ℃。同时堆芯中子监测子系统通过测量一系列沿反应堆堆芯高度布置的7个自给能探测器(self-powered neutron detector, SPND)同时产生的信号实现堆芯中子通量的在线连续测量。其主要通过深入压力容器内堆芯的中子-温度探测器，其微弱信号经过电缆传输到后端信号处理机柜，并经过信号的放大、滤波等后进行信号处理，进行中子通量的实时监测。堆芯中子监测系统主要实现以下功能：①对SPND信号进行调理和采集，去除附加信号；②对SPND信号进行延迟补偿，消除延迟效应；③对延迟补偿后的SPND信号进行电荷累积计算；④测量SPND的绝缘电阻，补偿泄漏电流并判断探测器是否故障；⑤将延迟补偿前后的信号和累积电荷值送至堆芯监测机柜，为其提供计算依据。

堆芯中子测量系统主要包含中子-温度探测器和中子信号处理机柜，堆芯中子通量信号处理机柜主控机箱和附属的扩展机箱为核心模块，负责决策和输出控制，通信模块Ⅰ实现主控机箱与扩展机箱之间的通信，通信模块Ⅲ和网关实现与堆芯监测机柜间的通信，通信模块Ⅳ通过网关与SU服务器连接，实现维护和测试期间运行及维护过程的状态监控、信号显示及故障排查等功能，系统结构示意图如图1所示。

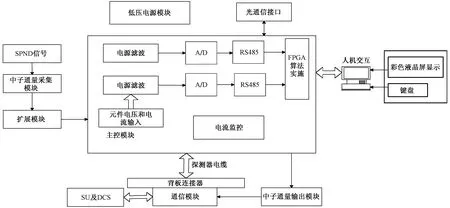
图1 中子通量测量系统结构示意图Fig.1 Structure diagram of neutron flux measurement system

2 中子通量测量系统可靠性模型

在进行可靠性分析时，先使用Markov模型对系统的状态进行划分，随后代入各个模块的可靠性数据得到每一模块的状态概率分布，然后根据中子通量测量系统原理图，构建出中子通量测量系统的GO图，再结合各个模块的状态概率分布，就可以计算出中子通量测量系统的状态概率分布，流程如图2所示。

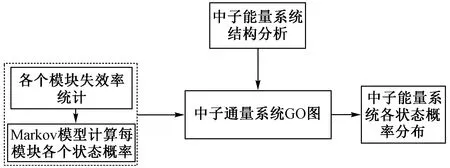
图2 中子通量测量系统可靠性模型流程图Fig.2 Flow chart of reliability model neutron flux measurement system

2.1 失效率计算

选用元器件计数法，在使用元器件计数法时，需要得知通用工作环境温度和常用工作应力条件下的失效率[14]，通用工作环境温度是指在不同环境条件下，各类器件在工作时通用的周围环境温度。堆芯运行状态监测仪用于对核反应堆内的各种参数进行测量，其机箱自身处于一种较平稳的工作环境温度。在元器件的标准中可以方便快捷地找到元器件在一些生产应用方面的质量控制水准，产品的质量档次的划分标准也是由此决定的，只有与产品息息相关的标准才是分级划分质量等级的依据。进行可靠性预计的标准参考文献[15]所提供的基础元器件失效率，并考虑到现场的环境温度、元器件选型、工艺技术等因素，按照失效率的数学模型计算得到。

依据著名的“澡盆曲线”[16]，在产品寿命期内元器件的可靠度一般呈现指数分布。各个元器件在模块的可靠性预计模型为串联模型，任何一个元器件失效将导致模块故障，数学表达式为

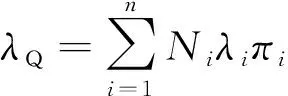
式(1)中：λQ为总失效率，10-6/h;λi为第i种元器件的通用失效率；Ni为第i种元器件的数量；n为产品的种类数；πi为第i种元器件的通用质量系数。

各个元器件代入上述的数学模型可得到各个模块的失效率如表1所示。

表1 各模块失效率计算结果

2.2 中子通量测量系统Markov状态空间模型

通过对中子通量测量子系统中模块的运行状态进行分析，将其划分为如下四个状态：正常运行状态(状态1)、隐性误动状态(状态2)、隐性拒动状态(状态3)和停运状态(状态4)。当模块中的自检装置没有检测出元器件的失效，则进入对应的隐性故障状态(包括隐性拒动和隐性误动)，当系统的隐性故障被触发后进入状态4，即停运状态。由此可得Markov状态空间模型如图3所示。

图3 中子通量测量系统Markov状态空间模型Fig.3 State space model Markov neutron flux measurement system

图中的参数说明：

(1)将RIC系统各个模块正常运行时的状态定义为状态1。

(2)当模块某些元件发生失效，但自检系统并未检查出时，模块处于误动状态，此时可能有两种情况：一种是隐性误动状态，定义为状态2；另一种是隐性拒动状态，定义为状态3。隐性误动可能会致使模块进入紧急状况并做出反应，隐性拒动会在有紧急状况时停止反应。此时模块虽然可以正常工作，但如果故障被外界的应力或电磁等干扰触发，模块会相应地进入失效状态。

(3)根据Markov过程理论，RIC系统对应模块从正常运作状态进入隐性误动状态与隐性拒动状态的转移率分别为λs、λD。

(4)在构建可靠性模型时，假设模块停运之后的修复率为μ1且经过修复之后可转移到状态1。

(5)RIC系统处于隐性故障时，如被定期检修发现，可被修复转移到正常运行状态；将对应模块由隐性拒动和误动转移到状态1的转移率分别设为μ2、μ3。

(6)RIC系统处于隐性故障时，可能被外界应力触发从而进入状态4。将对应模块从状态2和状态3被触发时进入停运状态的转移率分别设为设λe和λN。并且模块处于隐性误动状态时可能转移为隐性拒动状态，状态转移率设为λP。

2.3 Markov状态空间模型

根据图2中子通量测量系统Markov状态空间模型和Markov理论的无记忆性，可建立其状态空间方程，即

式(1)中：P为中子通量测量系统在ti时刻的状态分布；T为状态转移矩阵，其表达式为

转移矩阵数据关系式为

此处只关心P的稳态解，采用时间间隔数量趋于无穷时的平稳状态，即Markov过程将收敛于稳态概率值，此时有

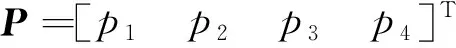
式(5)中：p1为对应系统正常运行的概率；p2为对应系统隐性误动的概率；p3为对应系统隐性拒动的概率；p4为对应系统停运的概率。

在式(3)中，q12、q22、q33、q44是与系统状态有关的指数分布，也是矩阵T的对角线元素，分别为

q11=-(λs+λD+λ) (6)

q22=-(λe+μ2+λD) (7)

q33=-(λN+μ3) (8)

q44=-μ1(9)

其状态转移矩阵可改写为

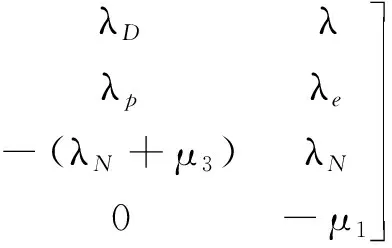
2.4 中子通量测量系统GO图模型

GO法是一种系统概率分析技术[17]，它采用图形演绎的方式，把系统原理图、流程图或工程图直接按一定规则翻译成GO图[18]，如图4所示。系统中的元件、部件或子系统统称为操作符，系统中各模块的逻辑关系在GO图中也用操作符和信号的流向来表示。本文采用GO图进行可靠性分析的步骤如下：

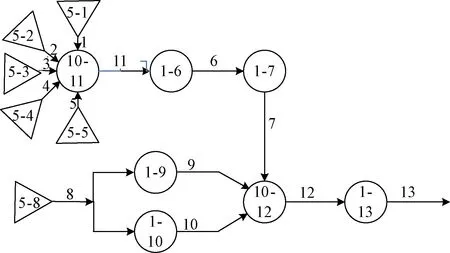
图4 中子通量测量系统GO图Fig.4 GO of neutron flux measurement system

(1)分析中子通量测量系统的基本原理，清楚各模块之间的逻辑结构。

(2)剖析模块功能及其输入和输出信号，明确它们之间的逻辑关系，从而确定对应模块的操作符，选择使用的操作符为第1、5、10类操作符。

(3)以信号流的顺序，根据系统逻辑的进程，分别连接各操作符生成GO图。

(4)按照第1、5、10类操作符的运算规则，依照信号流向得到系统的输出状态和状态概率。

本文方法的中子通量测量系统状态相对复杂，对于多状态系统[19]，用0，1，…，N等不同的数字来代表各操作符处于何种状态，各个状态相对应的概率为P(0),P(1),…，P(N)。其状态概率计算公式为

P(1)+P(2)+…+P(N)=1 (11)

因为已经通过建立Markov模型对各个模块等划分为了四个状态，将状态的分布看作模块所处状态的概率，所以用1、2、3、4四个状态值来代表模块所处不同的状态，概率定义为P(1)、P(2)、P(3)、P(4)。状态概率的计算公式可以表达为

P(1)+P(2)+P(3)+P(4)=1 (12)

中子通量测量子系统各模块与GO图中操作符的对应关系如表2所示。

表2 中子通量测量系统操作符

3 算例分析

通过建立中子通量测量系统的Markov状态空间模型[20]，得到各模块的状态概率，通过对状态划分进行分析，模块处于隐性故障状态时只要未触发仍可正常工作，因此中子通量测量系统的可用度定义为

A=p1+p2+p3(13)

代入GO图中进行计算，从而可以得知整个系统处于各个状态的概率。以信号采集模块为例，结合预制堆芯中子通量测量子系统运行情况，给出各参数取值如表3所示。

表3 信号采集模块Markov状态转移空间图参数

由图3的Markov模型，根据式(9)生成状态转移矩阵，即

根据式(12)计算出中子通量采集模块处于各状态的概率为：q1=0.975 75,q2=0.017 98,q3=0.006 24,q4=0.000 03。同样的，计算出其他模块处于各个状态的概率如表4所示。

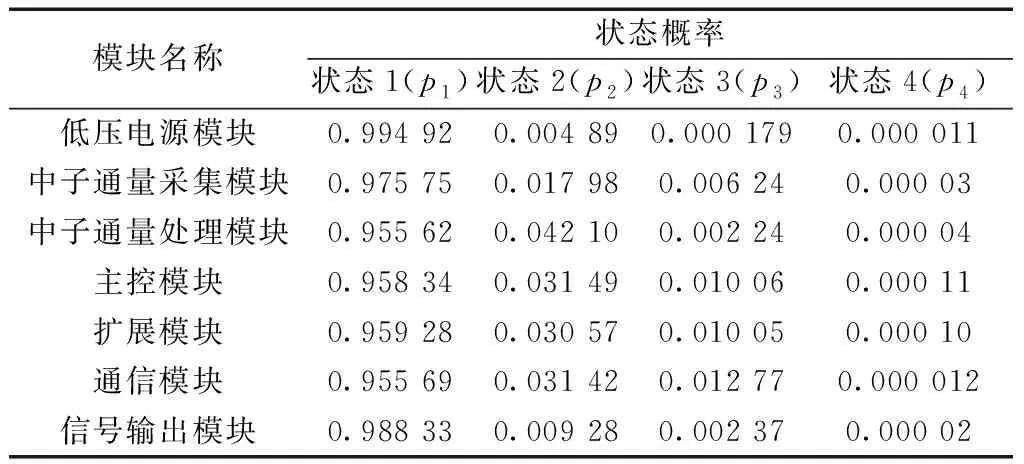
表4 中子通量测量系统各模块状态概率

得到各个模块在四个状态下的概率分布之后，将其代入RIC系统的GO图，并作为初始计算值计算得到中子通量监测子系统的系统状态概率，结果如表5所示。

表5 中子通量测量系统状态概率分布及可用度

经过计算可得预制中子通量测量子系统的可用度A=99.74%，且系统处于状态4(停运)的概率为0.361%，可靠性较高。从表4中子通量测量子系统状态概率分布来看，系统处于状态2、状态3的概率共为3.112%。但在实际运行时，因为会对系统进行定期检修，减少其触发隐性故障致使系统停运的可能性；因为自检系统存在可能无法察觉隐性故障而未统计系统处于状态2和状态3的情况，再实际运行中系统处于状态1的概率要更高一些，也验证了本文方法的正确性。

4 结论

针对目前堆芯运行状态监测仪结构复杂、可靠性要求日益苛刻的状况，创新性地将Markov模型和GO图进行结合，对RIC系统进行了可靠性方面的分析。首先利用Markov概念和随机过程方法，通过将系统从完全正常到停止工作之间的多种工作状态进行了划分，建立堆芯运行状态监测仪的Markov多状态可靠性分析模型，求出各个模块不同状态下的状态概率；然后利用GO法，根据系统原理建立GO图，进行系统可用度的计算，预计结果表明中子通量测量子系统的可用度为99.74%，满足系统可靠性的指标和项目设计要求。可靠性建模分析为RIC系统提供了定性的依据，具有重要意义。

经过分析和算例验证，中子通量测量子系统的可靠性较高，且使用本文方法可以求出中子通量测量系统处于各个状态的概率，也方便现场运行人员能够更加直观地观察系统运行状态，而非仅为烦琐且不甚准确的估计，本文方法还可以发现系统各模块的薄弱环节，为今后系统的改进和维护提供参考。