近代木结构柱-梁节点转动刚度及木材弹性模量的检测方法

刘剑珲, 徐 超, 欧阳煜

(上海大学土木工程系, 上海 200444)

历史保护木结构建筑的检测鉴定与加固设计中最大的困难在于: ①木结构节点构造复杂, 传力路径不明确, 在结构分析时无法确定木梁-木柱节点的转动刚度是0(铰接)、无穷大(刚接)或某一确定值(半刚性连接);②保护建筑不允许取样损坏, 无法确定木材的材料性能相关参数, 尤其是结构计算所需的弹性模量.基于此, 本工作对上海市历史保护建筑新泰仓库的木柱-木梁节点转动刚度及弹性模量的检测方法进行研究.

自20 世纪90 年代开始, 越来越多的专家学者围绕木结构建筑进行了详细的调查、周密的试验以及大量的科学分析.方东平等[1]在古建筑结构特性试验研究的基础上, 提出了木结构特征的三维有限元计算模型和分析方法, 第一次对古建筑木结构的斗栱和榫卯节点的力学性能进行定量研究.高大峰等[2-3]通过对木构架模型在水平反复荷载作用下的试验, 分析了中国古代木结构的变形特征及榫卯节点工作原理, 并通过榫卯节点的转动弯矩与转角试验数据, 确定了榫卯节点的转动刚度, 提出了结构在水平地震作用下的计算模型.姚侃等[4]通过对典型榫卯连接的力学分析和模型低周反复荷载试验, 研究了榫卯的半刚性连接特性和刚度退化的规律.杨艳华等[5]通过木结构榫卯节点模型试验, 得出影响连接刚度的主要因素是替木尺寸、榫头尺寸和卯孔对柱的削弱程度, 并利用最小二乘法对试验数据进行处理, 得出了榫头尺寸及卯孔对刚度影响的规律.赵鸿铁等[6]通过燕尾榫节点木构架的低周反复荷载试验, 得到弯矩-转角滞回曲线及骨架曲线, 以及榫卯节点半刚性连接特性和节点刚度退化的规律.谢启芳等[7]基于拟静力试验结果、节点力学平衡和变形协调等条件, 对燕尾榫节点弯矩-转角关系进行了理论推导, 提出以屈服点和极限点作为特征点的弯矩-转角双折线模型, 并给出特征点的计算公式.刘应扬等[8]通过对木框架足尺试件进行水平荷载试验, 并对梁柱节点足尺试件进行抗弯性能试验, 研究了梁柱节点的抗弯性能以及二者的传力机理和破坏模式.国外学者也不乏对古建筑木构架的研究.Lanius 等[9]对各种设有暗销的榫卯节点进行细致的研究, 并提出了节点和这类木结构的计算模型.Hanazato 等[10]研究了古建筑木材的材性及其对历史建筑力学性能的影响.Tanahashi 等[11]提出了梁柱节点的弹塑性模型(elasto-plastic pasternak model, EPM), 解决了古建筑木结构的静动力模拟问题.Judd等[12]通过试验分析了12 组不同连接角度下榫卯节点的抗拉力学性能, 得出连接角度减小可能增加节点强度但降低了结构延性, 以及当榫卯连接之间树纹相垂直时连接是最牢靠的结论.Artur 等[13]采用新旧栗木对传统木结构榫卯节点足尺模型进行试验, 并通过数值模拟对比分析了失效模型与极限荷载, 发现木材的抗压强度和接触面之间的法向刚度是影响极限荷载的主要因素.

由上可见, 目前对木结构节点的研究主要集中在传统木结构榫卯节点.上海地区解放前近代砖木工业建筑中的节点不同于中国传统的斗拱榫卯节点, 其木梁与木柱之间采用木梁+柱帽+木柱的连接方式, 相关研究较少.在历史保护建筑的保护工作中, 如何全面准确地做出结构既有承载力评定, 是不可或缺且意义重大的一环.本工作以上海市历史保护建筑新泰仓库中的木柱-木梁节点为研究对象, 提出了一种新的检测方法, 较好地解决了既有承载力检测鉴定与加固设计工作中遇到的主要问题.

1 试 验

1.1 木材物理特性及材性试验

参照GB/T 1933—2009《木材密度测定方法》和GB/T 1931—2009《木材含水率测定方法》, 在试验构件长度方向上截取尺寸为20 mm×20 mm×20 mm的7 个试件, 材料均采用花旗松-落叶松, 测得木材平均含水率为13.82%, 平均密度为0.54 g/cm3, 主要材性参数见表1.根据GB/T 1938—2009《木材顺纹抗拉强度试验方法》, 制作4 个标准试件进行顺纹抗拉强度试验, 材料均采用花旗松-落叶松, 测得木材顺纹抗拉弹性模量为12 598.48 MPa.根据GB/T 50329—2012《木结构试验方法标准》中的“附录B 木材顺纹受压应力应变曲线测定办法” 制作4 个试件, 材料均采用花旗松-落叶松, 试样尺寸为60 mm×60 mm×300 mm, 长度为顺纹方向, 测得木材顺纹抗压弹性模量为13 208.50 MPa.由试件顺纹抗拉试验、顺纹抗压试验测得的木材的弹性模量见表1.

表1 材性参数Table 1 Material parameters

图1 为本工作采用的木材本构模型[14], 其中σt、σc为受拉、受压屈服应力,εt、εc为受拉、受压屈服应变,εt,max、εc,max为受拉、受压极限应变,Et,t、Et,c为受拉、受压切线模量.

图1 木材本构模型[14]Fig.1 Constitutive model of the wood[14]

1.2 新泰仓库木柱-木梁结构静载试验

1.2.1 试验构件设计

选取新泰仓库二层一个典型的三跨木柱-木梁结构作为参照对象制作试验模型.在梁柱线刚度比值与原结构近似相等的大原则下, 取横截面与原结构的比例近似为1∶2;梁长度取为三跨相等, 与原结构的比例约为1∶3.5;柱的截面尺寸根据大原则确定, 与原结构的比例约为1∶2.2.木柱-木梁结构的缩尺模型如图2 所示.基于试验的资金有限等因素, 本工作对3 个木柱-木梁结构缩尺模型进行静载试验.

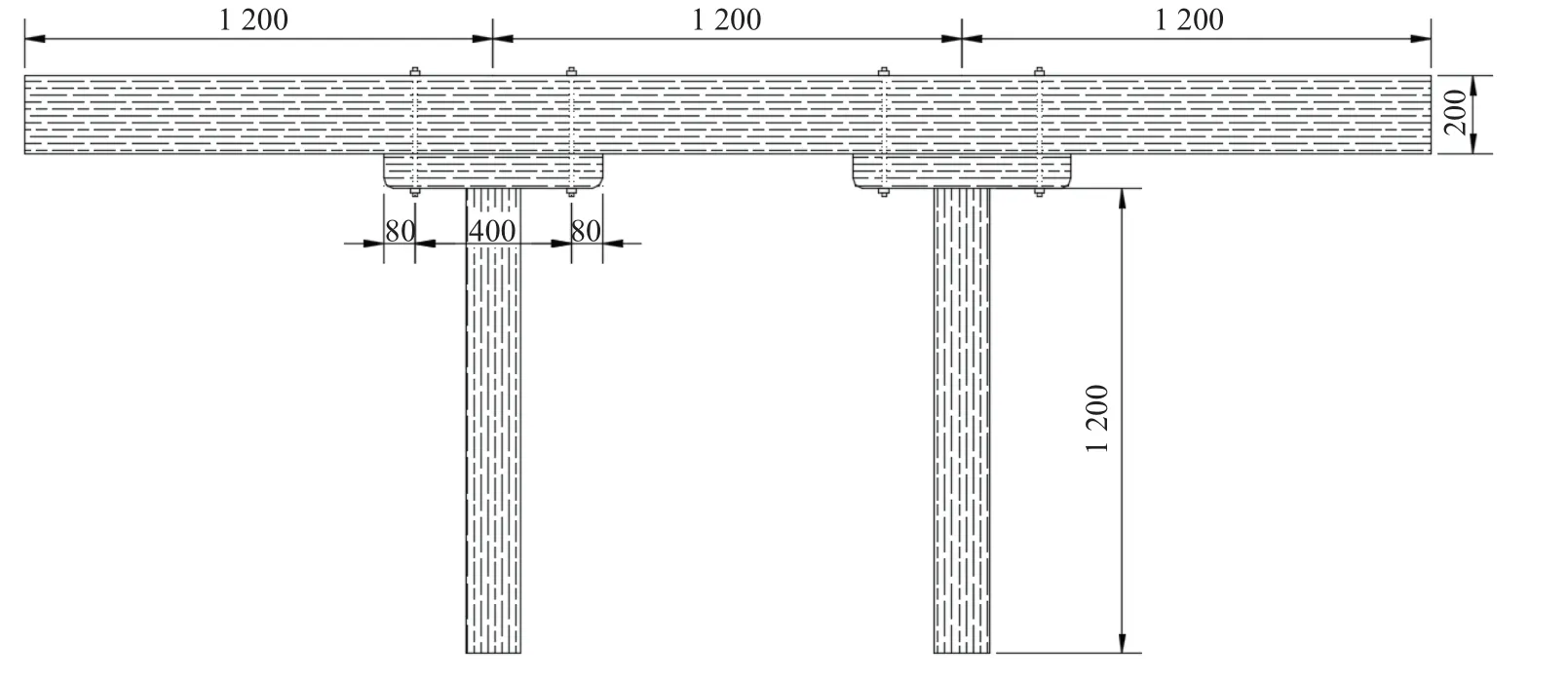
图2 木柱-木梁缩尺结构模型示意图(单位: mm)Fig.2 Schematic diagram of the wooden column-beam scale structure (Unit: mm)

木梁与木柱之间采用木梁+柱帽+木柱的连接方式, 柱帽孔洞的形状为长方体, 尺寸为80 mm×50 mm×30 mm, 长度方向与木梁长度方向一致;木梁以及柱帽的预钻孔径取值比螺栓直径大1 mm, 以保证节点顺利安装.相关构件的尺寸见表2.

表2 木柱-木梁构件尺寸Table 2 Component size of the wooden column-beam structure

1.2.2 试验加载方案

本工作采用电液伺服万能试验机在中跨木梁跨中位置顶部施加集中荷载, 示意图见图3.为防止在集中力施加过程中木梁顶部由于应力集中而过早损坏, 采用一块150 mm×150 mm的钢板作为加载垫板.根据实际工程受力情况, 木梁端部、木柱底端均为铰接.木柱下端采用刀口支座;木梁端部采用带刀口的钢板, 上下两块夹紧, 两块钢板以直径为30 mm 的螺栓锚固, 螺栓下部穿入预先准备好的地脚螺栓孔中, 以此形成铰支座.根据GB 50005—2017《木结构设计标准》的强度验算公式, 预测最大试验荷载集中力为114.3 kN.

图3 木柱-木梁缩尺结构的加载示意图Fig.3 Schematic diagram of loading of the wooden column-beam scale structure

试验采用分级加载: 第一级以5 kN/min 加载至30 kN, 持荷5 min;第二级以5 kN/min加载至60 kN, 持荷5 min;第三级开始以3 kN/min 的速度, 每次加载5 kN, 每级持荷10 min,直至结构破坏.构件破坏后, 以10 kN/min 匀速卸载, 直至试验机头与垫板完全分离.试验中位移传感器和应变片测点布置以及编号如图4 和5 所示.

图5 电阻式应变片测点布置图Fig.5 Layout of measuring point of the resistive strain gauge

2 试验结果及分析

2.1 主要试验结果

试件Test-01(见图6(a))以3 kN/min 加载至150 kN 后, 持荷10 min, 在持荷期间观察到中跨木梁挠度迅速增大, 在持荷到6 min 左右, 木梁沿着底部一个木节斜向上拉裂.试件Test-02(见图6(b))以3 kN/min 加载至165 kN 过程中, 在163 kN 时, 木梁底部木纤维拉断,随后沿着木梁侧面的木节斜向上拉裂.试件Test-03(见图6(c))以3 kN/min 加载至225 kN 过程中, 在221 kN 左右时, 构件发出剧烈崩坏声, 木梁底部木纤维整体拉断, 跨中挠度瞬间加大.木梁-木柱结构破坏形式均为梁跨中正截面受弯破坏.

图6 试件的破坏形式Fig.6 Failure modes of specimens

图7 为试验梁跨中荷载-位移曲线, 其中D-04 测点的位移已减去木柱竖向变形导致的支座位移.由于试件Test-01、Test-02 均有位于梁底面的木节, 承载力较低;而试件Test-03 的木节大部分位于梁顶面, 梁底面基本没有木节缺陷, 承载力较高.木节的存在对结构的承载力有着极大的削弱作用, 特别是当其位置靠近受拉区时, 尤为严重, 在实际工程检测中要密切关注木节所处位置带来的影响以及危害.另外, 试验中发现, 木梁的变形基本符合平截面假定.由图7(b)可以发现, 木柱发生较大的弯曲变形, 木柱中部有较大的侧向位移, 说明木柱-木梁结构的节点具有一定的转动刚度, 能够传递一定的弯矩, 导致木柱并非处于轴心受压状态.

图7 中跨梁试验曲线Fig.7 Test curves of the middle span beam

2.2 木材弹性模量上、下限值

将试验模型简化为图8 所示的力学模型.为简化计算, 不考虑木垫梁的作用, 将木梁简化为连续等截面矩形梁, 并将木柱-木梁节点处的螺栓连接、榫卯连接的作用综合等效为具有旋转刚度K的旋转弹簧.理论上, 当K为0 时为铰接, 当K为无穷大时为刚接, 实际结构的旋转刚度必然介于铰接、刚接之间.在实际工程中, 连接对转动约束达到理想刚接的90%以上,可视为刚接;在外力作用下, 柱梁轴线夹角的改变量达到理想铰接的80%以上, 可视为铰接;半刚接则介于二者之间.

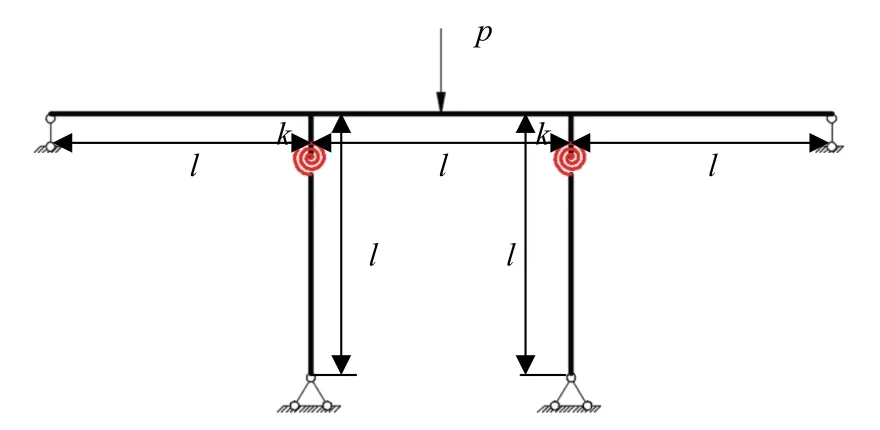
图8 木柱-木梁结构简化模型Fig.8 Simplified model of the wooden column-beam structure

在集中荷载p的作用下, 木梁木柱节点为铰接或刚接时, 木梁跨中挠度w分别为[15]

式中:E、G分别为构件木材的弹性模量与剪切模量;I、A分别为构件的惯性矩与截面面积;k为剪切系数, 对于矩形截面取k=1.2.

基于木材本构特性, 顺纹弹性模量与对应方向的剪切模量的比值为0.075[16], 即有

将试件尺寸、试验荷载值和相关材性参数代入式(1)和(2), 可通过每一级荷载下的跨中挠度计算相应的弹性模量值.当分别假定节点为铰接、刚接时, 计算出的弹性模量必然为真实弹性模量的上限值、下限值.采用这个方法可以确定木材真实弹性模量的取值范围.用于弹性模量识别的荷载区间取40∼120 kN, 以剔除前期加载、后期进入塑性阶段的离散性.根据试验成果计算所得的弹性模量上限值、下限值, 结果如图9 所示.铰接模型识别所得的弹性模量平均值作为上限值, 刚接模型识别所得的弹性模量平均值作为下限值, 真实的弹性模量值界定在一个较小的范围内.由图9 可知, 通过试验测定得到的弹性模量值界定在一定范围内, 上、下限最大差仅为1 784 MPa, 最大误差为15%.

图9 弹性模量的上限值、下限值Fig.9 Upper and lower limits of elastic modulus

根据GB 50005—2017《木结构设计标准》可知, 花旗松-落叶松的弹性模量取值为10 000 MPa, 与试验相比较, Test-01 较为接近, 而Test-02 和Test-03 的误差为4%∼37.6%.考虑到木材的离散性, 此误差区间属于合理范围.

2.3 木材弹性模量

木柱-木梁节点是半刚性连接, 具有一定的转动刚度, 因此木柱受弯变形, 引起木柱中部侧移.柱端弯矩的传递是造成木柱中部侧向位移的直接影响因素, 而传递弯矩的大小反映了节点的连接性能.将图8 所示的模型利用对称性简化为“木梁”和“木柱”两部分, 并将旋转刚度K的作用等效为传递弯矩M, 分别作用于两个结构体系对应位置(见图10).

图10 木梁-木柱简化模型受力示意图Fig.10 Force diagram of wooden column-beam simplified model

在跨中集中荷载p和木柱中部侧向位移∆2的作用下, 木梁跨中挠度为

以式(3)反算得到考虑节点半刚性连接的弹性模量半刚性测定值, 半刚性测定值的平均值即为弹性模量平均值(见图11).

铰接和刚接模型结合试验数据, 可以得到弹性模量上限值和下限值, 真实弹性模量(即半刚性测定值)必然处于二者之间.采用半刚性模型结合试验数据, Test-01、Test-02、Test-03 试件测定的弹性模量平均值分别为9 413、11 200、12 545 MPa.最终确定本次试验木材的弹性模量为11 052 MPa.由图11 可以看出, 构件荷载试验确定的弹性模量值略小于材性试验所得值, 这可能是木柱-木梁结构本身尺寸较大, 初始缺陷较多, 而材性试验中的木材由于试件尺寸小, 初始缺陷少, 故而测定所得的弹性模量相对较高.但是对于实际工程结构而言, 对于木材这种离散性较大的材料, 小试件材性试验测定的弹性模量反而是不准确的.

图11 试件弹性模量的确定Fig.11 Determination of elastic modulus of test pieces

2.4 柱-梁节点转动刚度识别

通过试验可以发现, 木柱-木梁节点呈现出典型的半刚性特征.图12 为木柱-木梁结构变形图.图12 中跨梁跨中挠度为∆1, 柱中部侧向位移为∆2, 二者对应节点处转角分别为α、β.在竖向荷载p作用下, 木梁、木柱中部的变形∆1、∆2与其对应的转角α、β近似有如下关系:

图12 木柱-木梁结构在跨中集中力作用下的变形图Fig.12 Deformation diagram of wooden column-beam structure under concentrated force

木柱与木梁的相对转角φ=α −β.木柱中部侧向位移∆2与柱端弯矩M存在如下关系:

木材弹性模量取11 052 MPa, 可得到竖向荷载p作用下木柱-木梁节点处的弯矩与相对转角的关系曲线(见图13).

图13 木柱-木梁节点M-φ 图拟合曲线Fig.13 Fitting curves of M-φ diagram of nodes of the wooden column-beam structure

根据图13 中曲线的斜率变化发现, 在弯矩逐步增加过程中, 转角的发展速率变快, 即节点转动刚度不是恒定不变的, 而是逐步降低.从图13 可以看出, 虽然3 次试验中木材品种、尺寸规格、加载方式均相同, 但由于木材本身的材料离散性以及每个木柱-木梁节点连接的施工误差, 转动刚度具有一定的离散性.

为得到木柱-木梁节点转动刚度的变化规律, 以M-φ曲线斜率明显变化点作为节点刚度的变化转折点, 将试验所得M-φ曲线, 用origin9.1 拟合成两段线性函数.由图13可见: 当0<φ <0.001 52 rad 时, 木柱-木梁节点转动刚度K= 1 077.21 kN·m/rad;当0.001 52 rad<φ <0.008 rad 时K= 294.64 kN·m/rad.木柱-木梁节点转动刚度较大, 试件中木柱与木梁的相对转角φ最大仅为0.014, 呈现出该连接良好的半刚性, 因此设计单位把该连接当成铰接可能是不合适的.

3 结 论

本工作以上海市历史保护建筑新泰仓库为对象, 通过3 个木柱-木梁结构缩尺模型的静载试验, 研究了既有木结构建筑特殊柱-梁节点转动刚度及弹性模量的检测方法, 主要结论如下:

(1) 采用静力加载试验, 通过量测木梁跨中竖向位移、木柱中部侧向位移, 结合相关计算分析, 研究了既有木结构建筑的材料性能, 可以相对准确地确定木材弹性模量的上、下限值,以及木材弹性模量平均值.

(2) 通过木柱-木梁结构的静载试验, 发现木柱-木梁节点具有明显的半刚性连接特征, 节点刚度随荷载的变化而变化;通过弯矩与相对转角的关系曲线进行分段线性拟合, 从而确定了木柱-木梁节点的转动刚度变化规律.本工作中的转动刚度虽然介入了柱、梁的影响, 但对于目前的工程实践还是具有一定的参考意义.如何剔除柱、梁因素, 更为精确地确定转动刚度, 是今后研究改进的一个方向.

(3) 如果采用本工作中的方法进行现场荷载试验, 可以相对准确地确定既有木结构建筑柱-梁节点转动刚度及弹性模量, 这为类似的既有木结构建筑检测鉴定和加固设计提供了一种相对准确的方法.