不同曲率下预应力斜墩曲线连续刚构桥施工过程变形分析
2021-02-23王旭燚王银辉
陈 闯,王旭燚,2,王银辉*
(1.浙大宁波理工学院土木建筑工程学院,宁波 315100;2.重庆交通大学土木工程学院,重庆 400074)
曲线连续刚构桥结合了连续刚构桥跨越能力大、施工工艺成熟、受力合理、结构整体性好[1]和曲线桥对线路走向适应性强等特点,是现代桥梁建设的常用桥型之一。曲线连续刚构桥墩梁固结使得桥墩承受主梁偏心压力和扭矩的作用,桥墩的曲线外侧压应力较小甚至随弯曲程度的增大而出现拉应力。为了改善桥墩的受力状态,设计上将桥墩设计成朝曲线内侧成斜腿造型并在曲线外侧张拉预应力。预应力斜墩曲线连续刚构桥在悬臂施工过程中,主梁变形受自重、预应力、施工荷载、混凝土收缩徐变、曲率半径等影响外,斜墩的中心线在横桥向呈倾斜状态和桥墩预应力的分批次张拉都会增加桥墩在悬臂施工过程中受力和变形的复杂性,进而加剧主梁变形的复杂性和控制的难度。
曲线连续刚构桥的主要受力特点是弯扭耦合[2],主梁除产生竖向变形外,还存在径向和扭转变形[3-4]。石雪飞等[5]分析了曲率和墩高对自重作用下高墩大跨曲线连续刚构桥最大悬臂状态空间变形的影响,研究发现,竖向变形、径向变形和扭转变形均随曲率半径的减小而增大,墩高放大了曲率对变形的影响;王钧利等[6]系统地研究了高墩大跨曲线连续刚构桥最大悬臂状态空间变形与圆心角的关系,悬臂端的竖向位移、径向位移和墩顶径向位移随圆心角的增大而增大;陈淮等[7]分析了高墩大跨曲线连续刚构桥各空间位移的组成,并指出桥墩的弯曲变形会进一步加大主梁的径向位移和扭转变形。随着曲线连续刚构桥,特别是高墩曲线连续刚构桥的广泛应用,桥墩变形对曲线连续刚构桥空间变形的影响逐渐受到重视;褚文涛等[8]指出曲线连续刚构桥施工过程的径向位移由桥墩横向弯曲和主梁自身径向位移组成;Hao等[9]指出曲线连续刚构桥施工过程主梁扭转角由主梁自身扭转、桥墩弯曲产生的附加扭转角以及几何曲率组成;崔颖波等[10]、Suo[11]、张柳春[12]和陈龙宇等[13]分析了高墩曲线连续刚构桥的空间变形;王存国等[14]分析了某跨铁小半径刚构-连续梁桥的空间变形。前人研究表明,桥墩的横向弯曲是主梁径向变形的主要原因,主梁在墩顶处径向位移最大并向悬臂端逐渐减小。蒋严波等[15]研究发现高墩曲线连续刚构桥主墩径向位移随高度增加呈线性变化;刘文忠等[16]指出曲线连续刚构桥主梁径向位移随墩高增加而增大;黄斌等[3]研究发现高墩大跨小半径曲线连续刚构桥主梁的最大扭转位移和径向位移均产生在墩顶附近;王胜杰等[17]分析了曲线连续刚构桥主梁径向位移产生的原因,并用力学分析方法推导了桥墩顶径向位移的计算公式。前人研究主要集中在高墩曲线连续刚构桥空间变形,而关于斜墩,特别是预应力斜墩曲线连续刚构桥悬臂施工过程中的空间变形的研究鲜有报道。因此,有必要分析预应力斜墩曲线连续刚构桥的空间变形及其随曲率半径的变化规律。
鉴于此,首先采用力学方法推导了悬臂施工过程斜墩分别在自重和预应力作用下墩顶横向位移和转角的计算公式,从理论上阐释了预应力斜墩曲线连续刚构桥悬臂施工过程中空间变形的主要规律;然后以宁波某跨铁路大跨不对称小半径曲线连续刚构桥为工程背景,分析了预应力斜墩曲线连续刚构桥空间变形特征;最后,建立了不同曲率半径的曲线连续刚构桥和直线连续刚构桥数值模型,分析了悬臂施工过程中自重、预应力、挂篮荷载和混凝土收缩徐变等作用下曲率半径对主梁空间变形的影响规律。通过揭示该类桥墩对曲线连续刚构桥空间变形的影响规律,以期为该类桥梁设计和施工过程变形的控制提供借鉴。
1 斜墩横向位移和转角计算理论
1.1 曲梁偏压下曲线连续刚构桥斜墩横向位移和转角计算理论
自重作用下曲梁对桥墩的偏压作用可以分解为竖向压力(F)和附加弯矩(M0)。以墩顶中心为原点,曲梁中心线的切线方向为z轴,曲线径向指向圆心为y轴建立坐标系,如图1所示。设曲梁悬臂长度为l,质量线密度为m(z),曲梁中心线满足y=f(z)关系式。
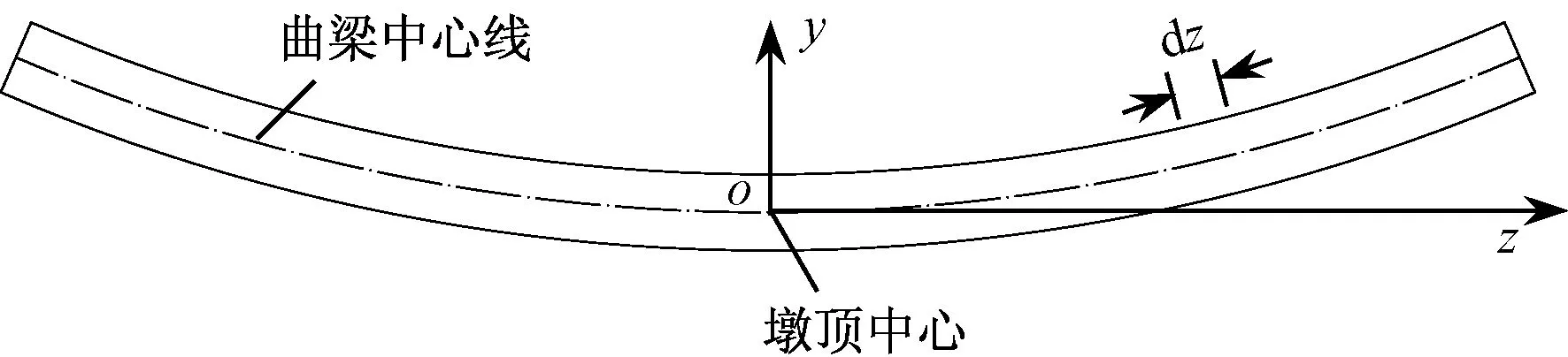
图1 曲梁平面示意图
取曲梁上任一微段(dz),则该微段的质量为m(z)dz,偏心距为f(z),因此,该微段对桥墩的竖向压力和附加弯矩分别为
dF=m(z)gdz
(1)
dM=-m(z)gf(z)dz
(2)
式中:g为重力加速度。
悬臂长l的主梁对桥墩的竖向压力和附加弯矩分别为
(3)
(4)
为简化推导,以矩形截面斜墩为例,取桥墩顺桥向宽度(b)沿墩高(h)不变,横桥向宽度由墩顶向墩底线性增大,墩顶横桥向宽为a,墩底横桥向宽为c,如图2所示。假设桥墩为均质、连续、各向同性的材料,并已知弹性模量为E。

图2 斜墩构造简图
因桥墩中心线倾斜,桥墩除承受主梁的附加弯矩M0外,还承受压力偏离桥墩各截面中心而产生的弯矩。主梁压力引起的斜墩任一截面x处的弯矩M1(x)为
(5)
因此,斜墩任一截面的总弯矩为
(6)
若忽略轴向压力和剪力对斜墩变形的影响,可利用梁的挠曲线近似微分方程[式(7)]进行积分,并通过桥墩的边界条件确定积分常数,最终可得到该墩在主梁压力和附加弯矩作用下的挠曲线方程。
(7)
式(7)中:ω″为梁的挠曲线方程。
斜墩任一截面x处惯性矩为
(8)
对式(7)进行积分得
(9)
(10)
结合墩底x=h处,横向位移ω=0和转角ω′=0的边界条件,可解得C1和C2分别为
(11)
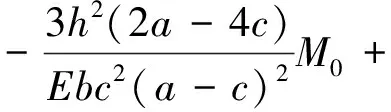
(12)
从而可以求得斜墩在曲梁压力F和附加弯矩M0作用下墩顶x=0处横向位移和转角分别为
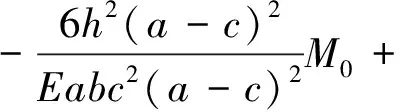
(13)
(14)

因此,曲线连续刚构桥悬臂施工前期,主梁对斜墩的作用以压力为主,桥墩墩顶会产生向曲线外侧的横向位移和转角,进而带动主梁产生向曲线外侧的径向位移和扭转变形;随悬臂长度的增长,主梁对斜墩的附加弯矩急剧增大,桥墩墩顶会产生向曲线内侧的横向位移和转角,从而使得主梁产生向曲线内侧的径向位移和扭转变形。悬臂施工位移的累加特性决定了斜墩曲线连续刚构桥在悬臂施工初期,主梁产生向曲线外侧的径向位移和扭转变形,有效地减小了曲梁向曲线内侧的径向位移和扭转变形,对控制和减小曲梁径向位移和扭转变形具有重要意义。
1.2 预应力荷载作用下斜墩横向位移和转角计算理论
曲线连续刚构桥桥墩预应力往往布置在桥墩的曲线外侧,已知桥墩预应力钢束贯穿整个桥墩,预应力为Np,且距桥墩外边缘距离为t,如图3所示,其他参数如图2所示。
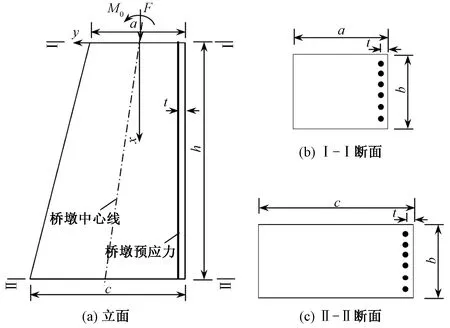
图3 预应力斜墩构造简图
桥墩预应力产生的横向弯矩为
(15)
若忽略轴向压力和剪力对斜墩变形的影响,可将式(15)、式(8)代入梁曲线微分方程[式(7)]进行积分,并结合墩底x=h处,ω=0和ω′=0的边界条件,可解得C1和C2分别为
(16)
(17)
从而可以求得斜墩在预应力(Np)作用下墩顶x=0处横向位移和转角分别为

(18)
(19)
由式(18)、式(19)可以看出,桥墩预应力使得桥墩墩顶产生向曲线外侧的横向位移和转角,且在桥墩构造参数确定的情况下,桥墩墩顶的横向位移和转角随预应力的增大而增大,进而带动主梁产生向曲线外侧的径向位移和扭转变形。因此,桥墩预应力在一定程度上也能减小曲梁产生向曲线内侧的横向位移和扭转变形。
2 数值模型简介
2.1 工程背景
以宁波市某上跨杭深、萧甬铁路的节点桥为工程背景。该桥是一座集大跨、小曲率半径、不对称和转体施工于一体的预应力混凝土连续刚构桥,全长301 m,桥跨布置为(68+138+95)m,如图4所示。桥梁上行线路中心线曲率半径为350 m,主梁截面顶板宽11 m,底板宽7 m。该桥采用不对称布跨,两T构悬臂长度分别为50 m和86 m,27号墩T构(小T构)主梁梁高5~9 m(按1.8次抛物线变化),对称悬臂浇筑13个节段,编号为Z0~Z13;28号墩T构(大T构)主梁梁高5~12 m(按1.8次抛物线变化),对称悬臂浇筑22个节段,编号为Y0~Y22。桥墩采用箱形截面,受多因素影响两桥墩墩高和截面均不对称,27号墩墩高17.65 m,墩顶横向宽7 m,纵向长5.5 m,墩底横向宽8.6 m,纵向长5.5 m;28号墩墩高16.55 m,墩顶横向宽7 m,纵向长6.5 m,墩底横向宽11.4 m,纵向长6.5 m,两桥墩均向曲线内侧呈斜腿造型。为改善桥墩的受力状态,在桥墩的曲线外侧张拉竖向预应力,如图5、图6所示,桥墩预应力在悬臂施工过程中分批张拉,即0#块施工完成后,张拉桥墩第一批预应力钢束QD1;Z5、Y7施工完成后,张拉第二批桥墩预应力QD2;Z10、Y14施工完成后,张拉第三批桥墩预应力QD3。

图4 立面布置图

图5 27号墩钢束布置图
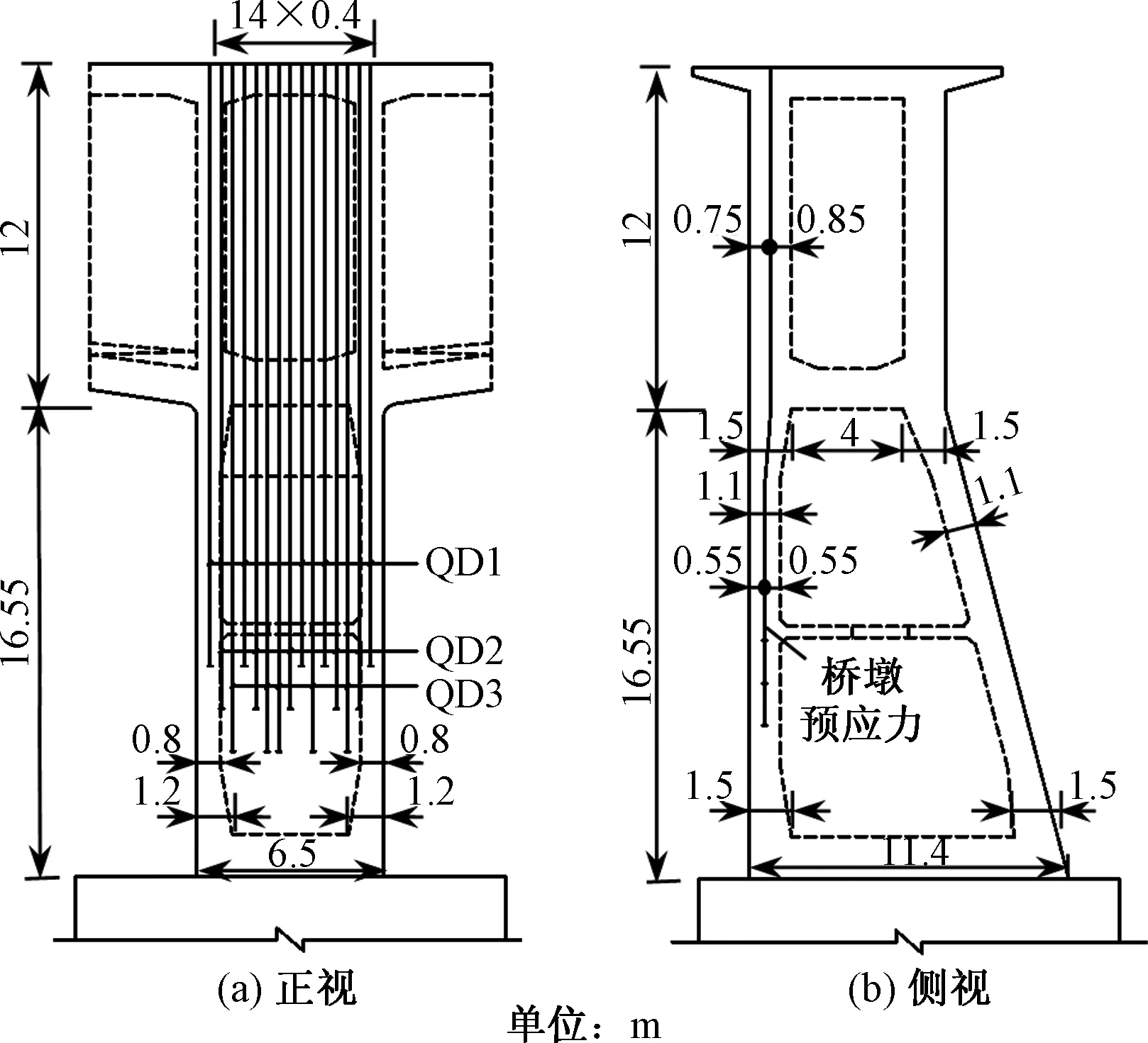
图6 28号墩钢束布置图
2.2 有限元模型简介
采用有限元软件Midas/Civil建立该桥计算模型如图7所示,全桥共881个单元和918个节点。计算模型中输入桥墩竖向普通钢筋,并在桥墩截面刚度计算中考虑其影响,主梁、桥墩、承台、桩基之间采用弹性-刚性连接,桩底采用固结约束。桩土相互作用根据地质资料,采用《公路桥涵地基与基础设计规范》(JTG3362—2019)的m法计算出各土层的土弹簧刚度,并作为边界条件直接施加在桩的节点上。梁端两侧按照实际支座情况建立约束,分别模拟纵向活动支座和双向活动支座,其中双向活动支座仅模拟竖向支撑,且竖向刚度取为5×106kN/m,纵向活动支座除模拟竖向支撑外,约束了径向位移。模型按照实际施工过程划分90个施工阶段,各节段悬臂施工分为挂篮就位、混凝土浇筑和预应力张拉3个施工阶段。曲梁自重扭矩通过节点扭矩施加。
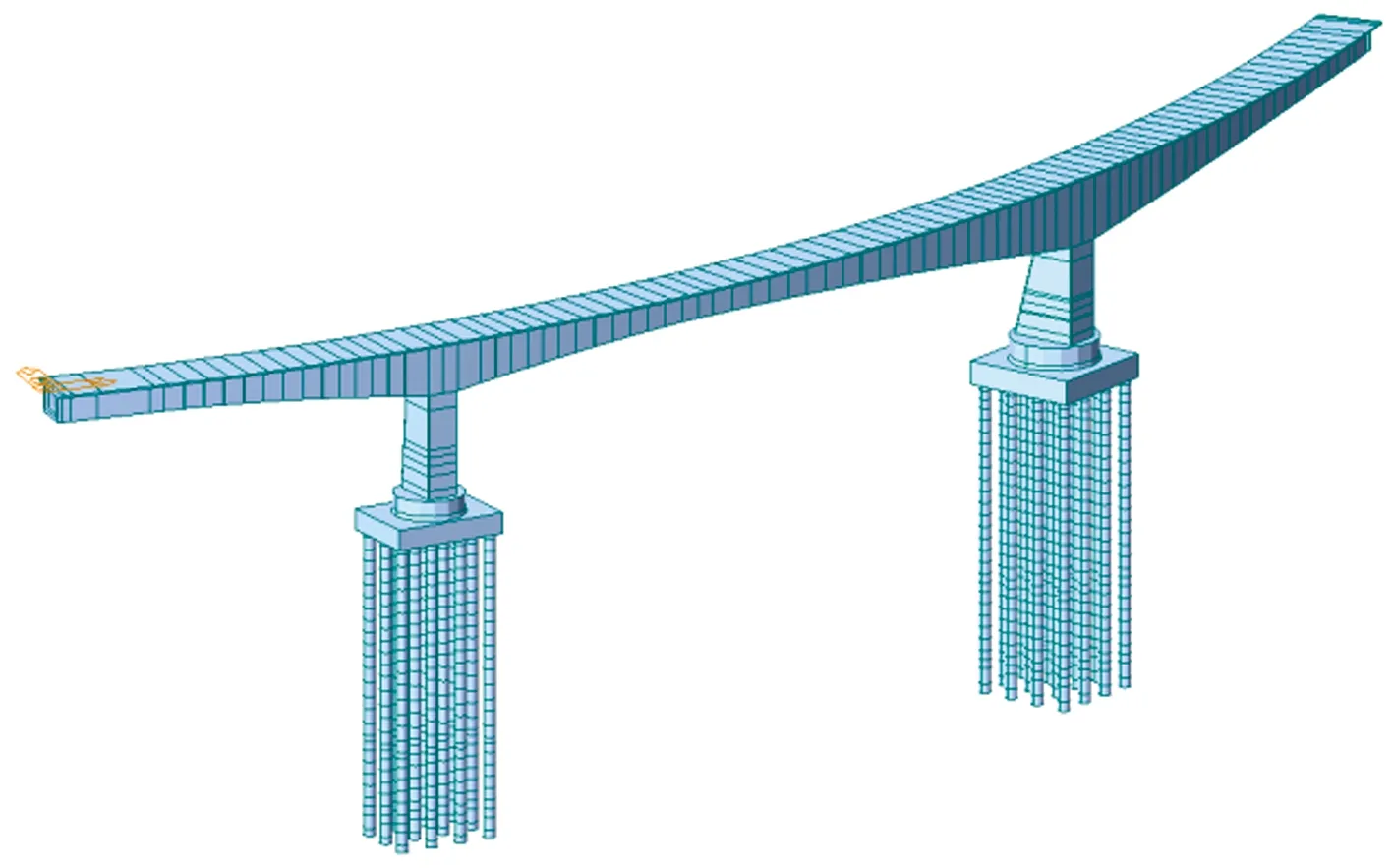
图7 有限元模型
3 预应力斜墩曲线连续刚构桥施工过程空间变形分析
以悬臂长度86 m的大T构为研究对象,分析最长悬臂状态主梁在各种荷载作用下的空间变形,如图8所示,其中合计表示4种荷载的组合效应。竖向位移以上挠为“+”,径向位移以沿曲线径向指向圆心为“+”,扭转变形以向曲线外侧转动(主梁曲线内侧高,外侧低)为“+”。
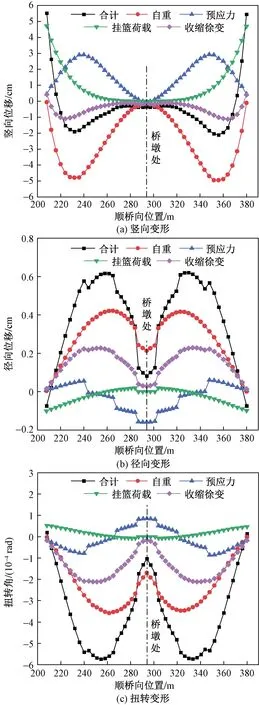
图8 最大悬臂状态曲线连续刚构桥主梁空间变形
由图8(a)可以看出,曲线连续刚构桥最大悬臂状态主梁竖向变形由悬臂根部向悬臂端先略微上挠后下挠再上挠,最大下挠出现在悬臂58 m处,其值为-1.9 cm,最大上挠出现在悬臂端处,上挠值为5.5 cm。主梁自重、预应力和挂篮荷载对竖向位移影响较大,预应力与自重作用效应相反,有效地减小主梁下挠,挂篮荷载作用是主梁悬臂端上挠的主要原因。由图8(b)、图8(c)可以看出,主梁产生向曲线内侧的径向位移和扭转变形,两者均由悬臂根部向悬臂端先增大后减小,最大径向位移为0.62 cm,出现在悬臂32.5 m处,最大扭转变形为-5.7×10-4rad,出现在悬臂36 m处。自重、预应力和混凝土收缩徐变对主梁的径向变形和扭转变形影响较大,自重作用下主梁径向位移和扭转变形由悬臂根部向悬臂端先增大后减小,预应力产生的径向位移和扭转变形均呈阶梯状,混凝土收缩徐变致使的主梁变形与组合效应的变形较一致。
4 曲率半径对桥梁施工过程变形的影响分析
为了探究不同曲率半径对斜墩曲线连续刚构桥空间变形的影响,分别建立曲率半径R为150、200、250、352.1、500、800 m、2 000 m的曲线连续刚构桥和直线连续刚构桥,分析曲率半径对主梁空间变形的影响规律。
4.1 不同曲率半径最大悬臂状态主梁的空间变形
不同曲率半径的曲线连续刚构桥主梁的竖向变形、径向变形和扭转变形如图9所示。
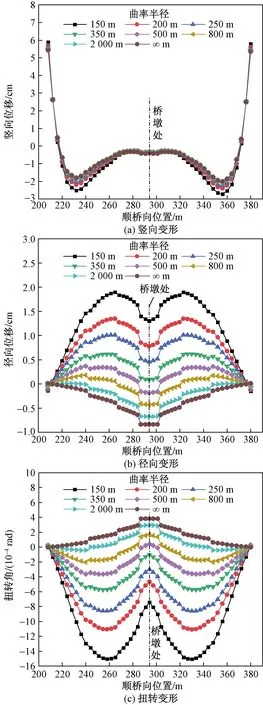
图9 不同曲率半径最大悬臂状态主梁空间变形
由图9可知,曲率半径对最大悬臂状态主梁的竖向变形、径向变形和扭转变形均有影响。曲梁的竖向变形规律与直梁一致,均由悬臂根部向悬臂端先略微上挠后下挠再上挠,曲梁的竖向变形随曲率半径的减小而增大,曲率半径为150 m的曲线连续刚构桥最大下挠比直线刚构桥大0.7 cm,最大上挠位移比直线桥大0.5 cm。直线连续刚构桥主梁始终产生向曲线外侧的径向位移和转动,小半径曲线连续刚构桥产生向曲线内侧的径向位移和转动,且由悬臂根部向悬臂端先增大后减小,产生这一现象的原因一方面是桥墩预应力使得桥墩向曲线外侧弯曲,另一方面是直线连续刚构桥主梁自重始终迫使斜墩产生向曲线外侧的弯曲变形,而曲线连续刚构桥主梁对桥墩的附加弯矩使得桥墩向曲线内侧偏位和转动,悬臂施工初期墩顶附近的主梁向曲线外侧的径向位移和扭转变形有效地减小了主梁向曲线内侧的径向位移和扭转变形。主梁径向变形和扭转变形的主要差异为曲梁的扭转变形墩顶“凹陷”较径向位移大,其主要原因在于径向变形和扭转变形均由桥墩致使的主梁位移和曲梁自身的变形组成,而曲梁自身的扭转变形对总扭转变形影响更大。
4.2 自重作用下不同曲率半径主梁的空间变形
自重作用下不同曲率半径的曲线连续刚构桥施工过程中主梁的竖向变形、径向变形和扭转变形如图10所示。

图10 自重作用下不同曲率半径主梁的空间变形
由图10可以看出,自重作用下曲线连续刚构桥竖向变形规律同直线连续刚构桥一致,曲率半径为150 m的曲线连续刚构桥最大下挠比直线刚构桥大0.5 cm。直线连续刚构桥在自重作用下产生向曲线外侧的径向位移和扭转变形,小半径曲线连续刚构桥产生向曲线内侧的径向位移和扭转变形,且由悬臂根部向悬臂端先增大后减小,原因是直线连续刚构桥主梁对桥墩只有竖向压力而无附加弯矩作用,因而斜墩产生向曲线外侧的弯曲变形,而曲线连续刚构桥主梁悬臂施工前期以压力为主,使得斜墩产生向曲线外侧的弯曲变形带动了主梁的偏位和转动,悬臂施工前期的结构变形减小了曲线桥后期向曲线内侧的径向位移和扭转变形。曲率半径越小,曲线连续刚构桥主梁最大径向位移和扭转变形的位置越靠近悬臂根部,如曲率半径500 m主梁的最大径向位移出现在悬臂32.5 m处,而曲率半径为150 m主梁的最大径向位移出现在悬臂25.5 m处,原因是曲率半径越小,主梁重心向曲线内侧内移速度越快,悬臂施工过程中桥墩越早向曲线内侧弯曲。受主梁自身扭转变形的影响,自重作用下主梁墩顶处扭转变形“凹陷”较横向变形大。
4.3 预应力作用下不同曲率半径主梁的空间变形
预应力作用下不同曲率半径的曲线连续刚构桥施工过程中主梁的竖向变形、径向变形和扭转变形如图11所示。
由图11可以看出,预应力主要使主梁产生与自重作用效应相反的竖向变形,其产生的径向变形和扭转变形较小。曲率半径对预应力作用下主梁的竖向变形基本无影响。受桥墩预应力的影响,直线连续刚构桥在预应力作用下的径向变形和扭转变形呈现出明显的阶梯状,曲线连续刚构桥主梁在阶梯状变形基础上向曲线内侧偏位和转动,主要原因是主梁预应力也会使主梁自身产生向曲线内侧的径向位移和扭转变形。
4.4 挂篮作用下不同曲率半径主梁的空间变形
挂篮作用下不同曲率半径的曲线连续刚构桥施工过程中主梁的竖向变形、径向变形和扭转变形如图12所示。

图12 挂篮作用下不同曲率半径主梁的空间变形
由图12可以看出,悬臂施工过程中挂篮从加载至卸载的过程会使主梁上挠、产生向曲线外侧的径向位移和扭转变形。主梁竖向挠度由悬臂根部向悬臂端逐渐增大,在悬臂25.5 m以内基本为零,最大竖向位移出现在悬臂端部,且随曲率半径减小而增大,曲率半径150 m的曲线连续刚构桥主梁悬臂端上翘5.1 cm,比直线连续刚构桥大0.5 cm。连续刚构桥墩顶径向位移和扭转变形基本为零,直线连续刚构桥悬臂部分主梁产生向曲线内侧的径向位移和扭转变形,原因是施工1号块的挂篮使得斜墩向曲线外侧弯曲,而挂篮的前移过程不会使桥墩进一步发生变形,挂篮卸载使桥墩恢复竖直状态的过程带动了主梁产生向曲线内侧的径向位移和扭转变形。曲线连续刚构桥悬臂部分主梁产生向曲线外侧的径向位移和扭转变形,且由悬臂根部向悬臂端逐渐增大,并随曲率半径的减小而增大,主要原因是随曲率半径的减小,挂篮产生的墩顶附加弯矩对桥墩和主梁的变形影响增大。
4.5 收缩徐变作用下不同曲率半径主梁的空间变形
混凝土收缩徐变作用下不同曲率半径的曲线连续刚构桥施工过程中主梁的竖向变形、径向变形和扭转变形如图13所示。

图13 收缩徐变作用下不同曲率半径主梁的空间变形
由图13可以看出,混凝土收缩徐变作用下主梁的竖向变形、径向变形和扭转变形与主梁最大悬臂状态的组合效应变形相类似,原因是收缩徐变的作用效应与结构受力历程密切相关。混凝土收缩徐变作用下,主梁的竖向变形随曲率半径的减小而增大,曲率半径150 m的曲线连续刚构桥主梁的最大下挠为-1.4 cm,比直线连续刚构桥大0.4 cm。直线连续刚构桥产生向曲线外侧的径向位移和扭转变形,小半径曲线连续刚构桥产生向曲线内侧的径向位移和扭转变形,且由悬臂根部向悬臂端先增大后减小。
5 结论
桥墩的预应力和斜腿造型对减小和控制曲线连续刚构桥主梁的径向位移和扭转变形具有重要意义,通过斜墩分别在曲梁偏压和桥墩预应力作用下墩顶横向位移和转角的力学分析,结合实际工程项目的曲线连续刚构桥、不同曲率半径的曲线连续刚构桥和直线连续刚构桥最大悬臂状态主梁的数值模拟分析,得出以下主要结论。
(1)预应力斜墩曲线连续刚构桥悬臂施工过程受桥墩构造和预应力的影响,前期主要产生向曲线外侧的径向位移和扭转变形,后期主要产生向曲线内侧的径向位移和扭转变形,从而表现出径向位移和扭转变形由悬臂根部向悬臂端先增大后减小的规律,且峰值随曲率半径的减小而向桥墩靠近。
(2)主梁的竖向变形主要受自重、预应力和挂篮荷载的影响,且各种荷载作用下的主梁竖向变形随曲率半径的减小而增大。
(3)各施工荷载对主梁径向变形和扭转变形的作用效应与曲率半径密切相关,直线连续刚构桥的径向位移和扭转变形产生于桥墩的横向变形,而曲线连续刚构桥还包含了曲梁自身的径向变形和扭转变形。
(4)挂篮荷载对主梁竖向变形的作用体现为其卸载致使的主梁上挠,对主梁径向位移和扭转变形的影响主要体现为挂篮对桥墩的压力和附加弯矩致使的桥墩变形所带动的主梁偏位和转动。
