考虑缝间流量不对称的裂缝井干扰试井分析方法
2021-02-23王慧萍吴嘉鑫张景丰程时清
王慧萍,吴嘉鑫,王 锋,张景丰,程时清*
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249; 2.延长油田股份有限公司靖边采油厂,靖边 718500)
当注采井网井距较小或井间存在高渗透通道及裂缝时,邻井对测试井关井压力恢复影响较大,导致压力导数曲线出现上翘或下掉的现象。早在20世纪70年代人们就开始进行井间干扰的试井研究。
Cinco等[1]创立了垂直裂缝有限导流理论模型。Uraiet等[2]把激动井考虑成均匀流量垂直裂缝,分别讨论了两井连线方向与裂缝面延伸方向夹角及井间无量纲距离对常规观察井压力响应的影响,确定裂缝延伸方向与位置。Mousli等[3]分别以常规直井和垂直裂缝井作为激动井,观察井假设为无限导流能力垂直裂缝井,激动井压裂井时则假设为均匀流量模型,讨论了干扰试井分析方法。Ma等[4]研究了天然裂缝发育油藏中的干扰试井,确定了裂缝的发育方向。Cherifi等[5]分别讨论了均匀流量模型、无限导流模型和有限导流模型的干扰试井分析方法。李成勇等[6]建立考虑观察井开井生产情形时的干扰试井模型。张秀华等[7]建立并求解了考虑井筒储集和表皮因子影响的复合干扰试井理论模型。张德志等[8]建立并求解了三重介质油藏的干扰试井解释模型。孙贺东[9]建立了无限大气藏多口直井系统干扰的试井分析模型。徐剑明等[10]利用裘比公式,考虑邻近气井压力降在观察井的变化规律,通过井底压力恢复曲线判断邻井的干扰影响。方冉[11]讨论了聚合物驱干扰试井模型以及包含注聚井的邻井干扰分析模型,得到了注聚井和产聚井的试井典型曲线,系统地分析了聚合物浓度和黏滞性等特性对试井曲线特征的影响。黄灿[12]建立了2口水平井的非均匀网格模型,分析了水平井井底压力的动态变化。程时清等[13]建立了多级压裂水平井注采井网干扰试井模型,判断出注采井连通性以及观察井的来水方向。随后,He等[14]考虑了水平井水平段内流体流动压力损失以及各压裂段产液量不均匀分布的特征,提出了基于多级压裂水平井不规则产液条件下的干扰试井模型。Qin等[15]建立了裂缝部分闭合压裂井多井干扰系统模型,该模型解决了单井模型试井解释裂缝半长与压裂设计裂缝半长相差较大的问题,但其裂缝模型具有无限导流能力,未考虑裂缝之间及其干扰井间的相互影响。Chu等[16]基于幂律模型的扩散指数建立了能够量化页岩油藏井间干扰的多级压裂水平井试井模型,利用干扰压力扩散指数来反映干扰源强弱,量化井间连通性。
现有多井干扰试井解释方法研究缝间流量不对称及裂缝相互干扰对邻井压力分析的影响较少,实际试井解释工作往往受限。对于大多数出现干扰现象的测试井,一般采用边界条件或复合油藏条件解释,得到错误的解释结果,可能误导油田开发政策调整。
1 缝间流量不对称的干扰试井模型
选取注水开发单元中的1口生产井作为干扰井,1口或多口生产井作为观察井,观察井和干扰井都压裂。在干扰试井过程中,干扰井的井底压力先通过裂缝传导至基质,再由基质传播到远处的观察井裂缝,也就是说,在观察井测压过程中既测量本井的压力变化,也测量到邻井生产或关井引起的压力变化。
由于存在邻井干扰作用,观察井裂缝表面线流量会受到干扰井生产的影响,反过来,干扰井裂缝表面线流量同样也会受到观察井生产影响,即同时考虑干扰井和观察井两井裂缝间的相互干扰作用。在干扰形成后,观察井和干扰井裂缝面线流量都将非对称分布。相同区块地层主应力方向一致,可以假设两井裂缝延伸方向平行。
存在邻井干扰下的压裂井试井模型基本假设为:①无限大地层中存在两口压裂井;②两压裂井压裂缝关于井筒对称分布,裂缝半长分别为xf1和xf2;③沿裂缝存在着压力降,裂缝内渗透率分别为kf1和kf2;④考虑干扰井与观察井的相互作用,裂缝间互相存在干扰,裂缝内流量将不再是对称分布;⑤两压裂井压裂缝延伸方向平行;⑥观察井以定产量q1生产,干扰井以定流量q2生产或注水。
以观察井为坐标原点建立直角坐标系,裂缝所在直线为x轴,两井间距离为L,井间连线与x轴正半轴的夹角为θ,激动井的坐标为(xL,yL)。邻井干扰的井位示意图如图1所示。
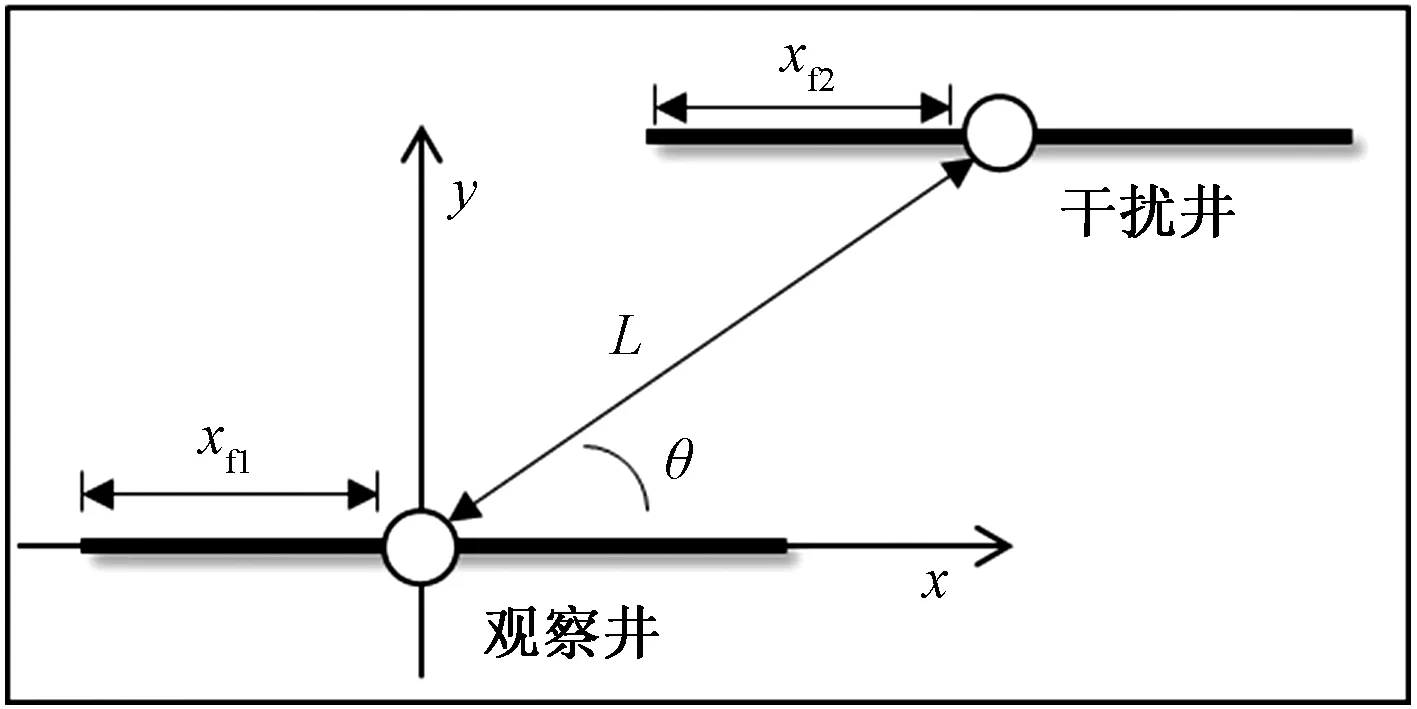
图1 邻井干扰的井位示意图
首先定义无量纲量:
式中:pD为无量纲井底压力;xD为无量纲横坐标;yD为无量纲纵坐标;tD为无量纲横时间;k为油层渗透率,10-3μm2;h为油层厚度,m;pi为原始油层压力,MPa;q1为测试井流量,m3/d;q2为干扰井流量,m3/d;μ为流体黏度,mPa.s;B为流体体积系数;pfD为无量纲裂缝表面压力;pf为裂缝表面压力,MPa;t为测试时间,h;φ为孔隙度;Ct为综合压缩系数,MPa-1;xf1为测试井裂缝半长,m;xf2为干扰井裂缝半长,m;CD为无量纲井储系数;C为井储系数,m3/MPa;CFD1为测试井无量纲裂缝导流系数;CFD2为干扰井无量纲裂缝导流系数;kf1为测试井裂缝渗透率,μm2;kf2为干扰井裂缝渗透率,μm2;wf1为测试井裂缝缝宽,m;wf2为干扰井裂缝缝宽,m;qD为无量纲流量;qfD1为测试井无量纲裂缝表面线流量;qfD2为干扰井无量纲裂缝表面线流量;qf1为测试井裂缝表面线流量,m2/d;qf2为干扰井裂缝表面线流量,m2/d;xL为两井横向距离,m。
为了建立无限大均质油藏中压裂井邻井干扰数学模型,以下将分别建立地层模型、观察井裂缝模型和干扰井裂缝模型,然后耦合得到井底压力计算模型。
1.1 地层渗流模型
地层某一位置的压降是由观察井和干扰井共同作用造成的,由观察井形成的压力降[9]为
(1)
式(1)中:K0为第二类零阶修正的Bessel函数;u为Laplace变换系数。
干扰井在地层某一处形成的压力降为
(2)
式(2)中:xLD为无量纲两井横向距离;yLD为无量纲两井横向距离。
于是无限大均质油藏中存在压裂井干扰下地层任意位置处压力降的表达式为
(3)
1.2 观察井裂缝模型
观察井裂缝内压力关系表达式[9]为
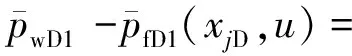
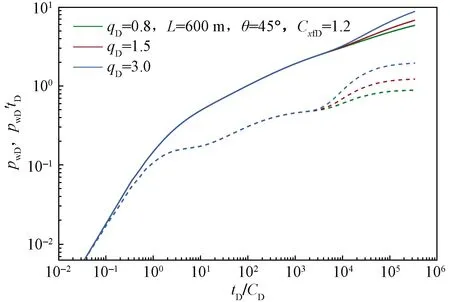
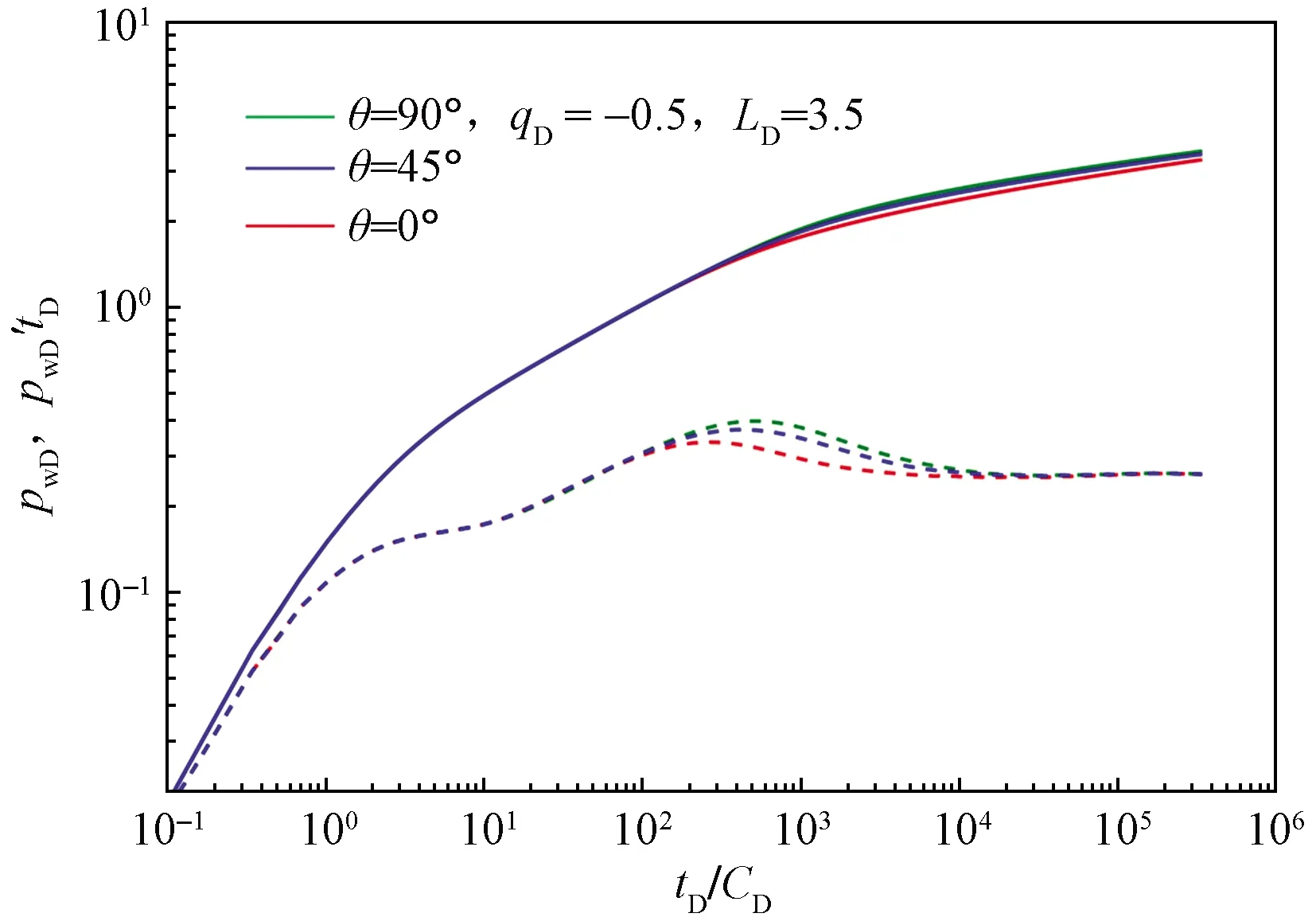
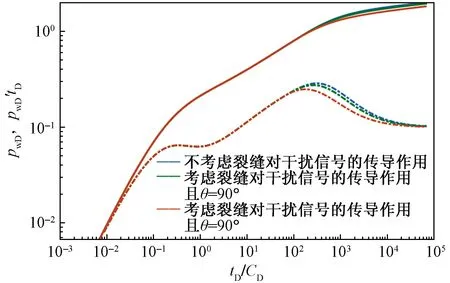
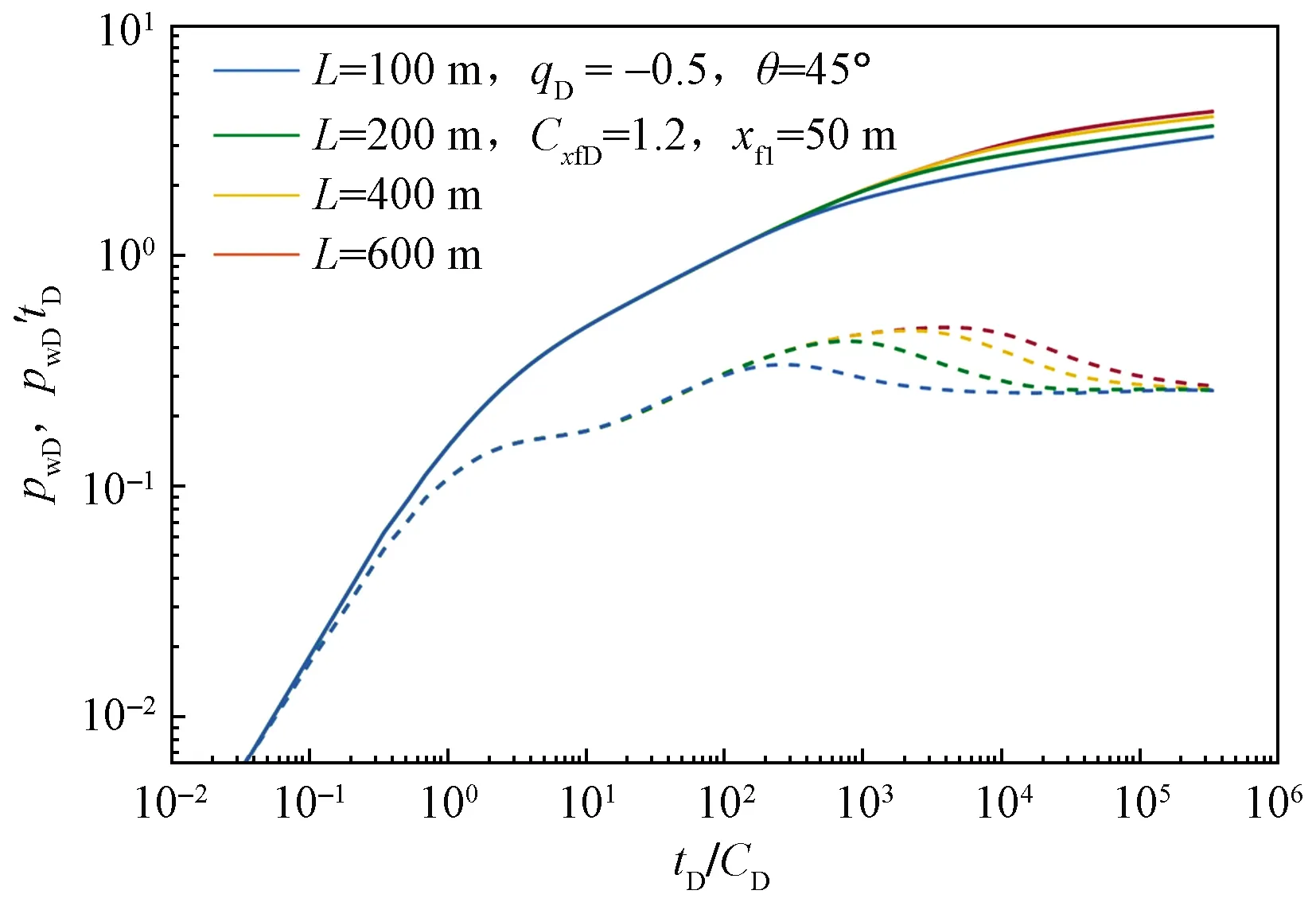
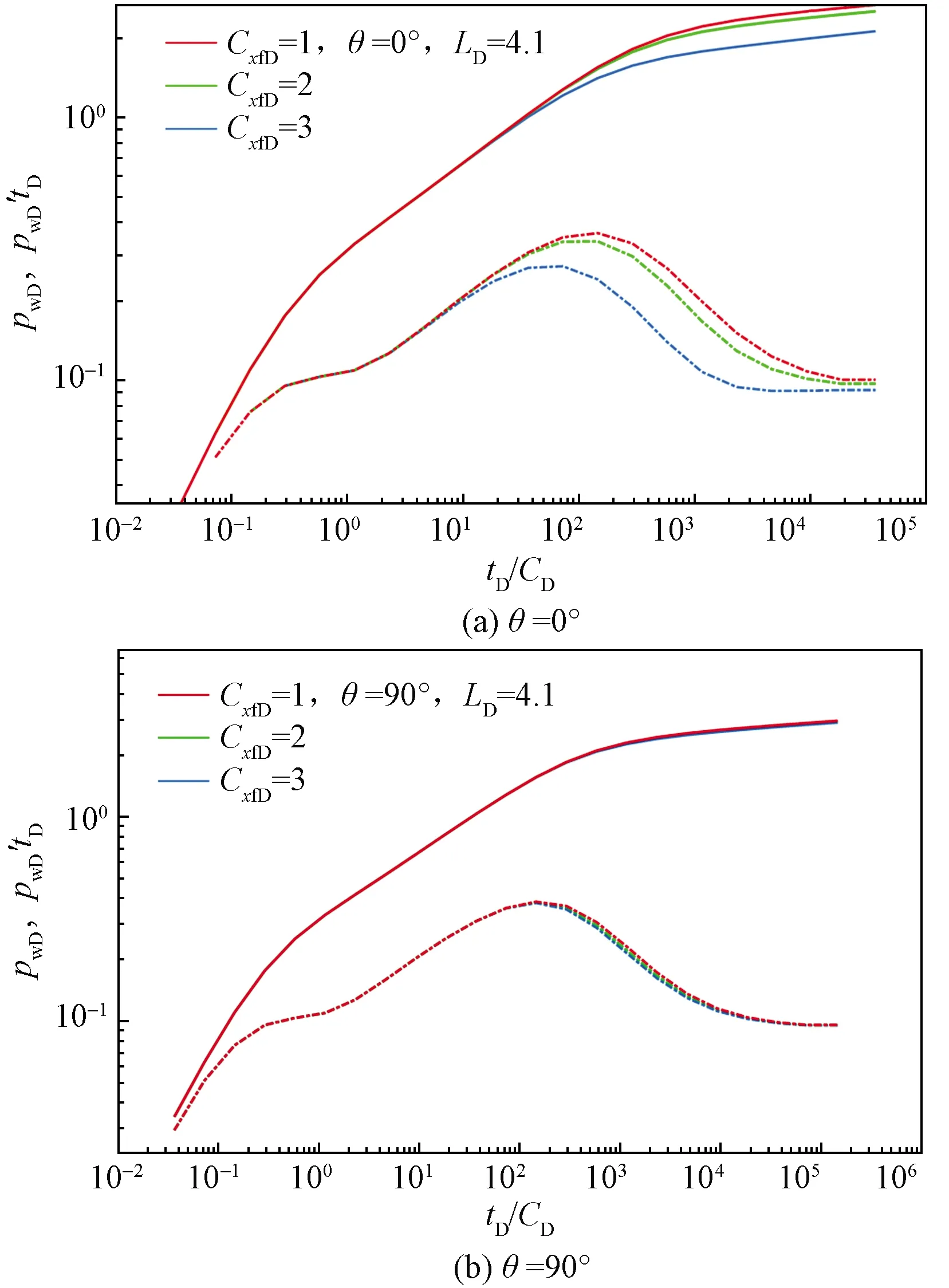
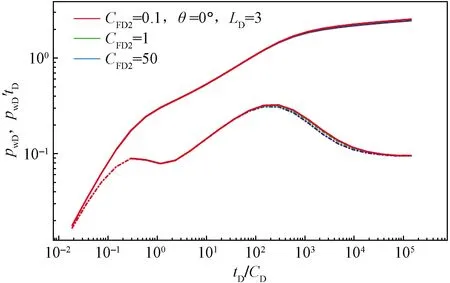
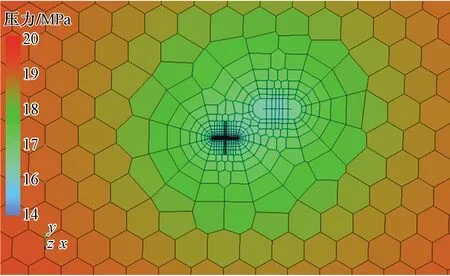
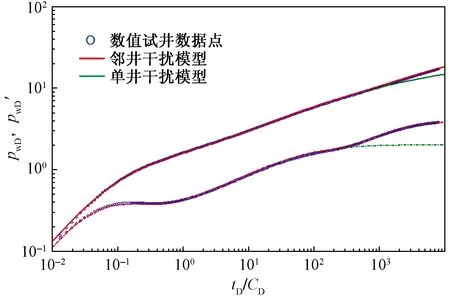
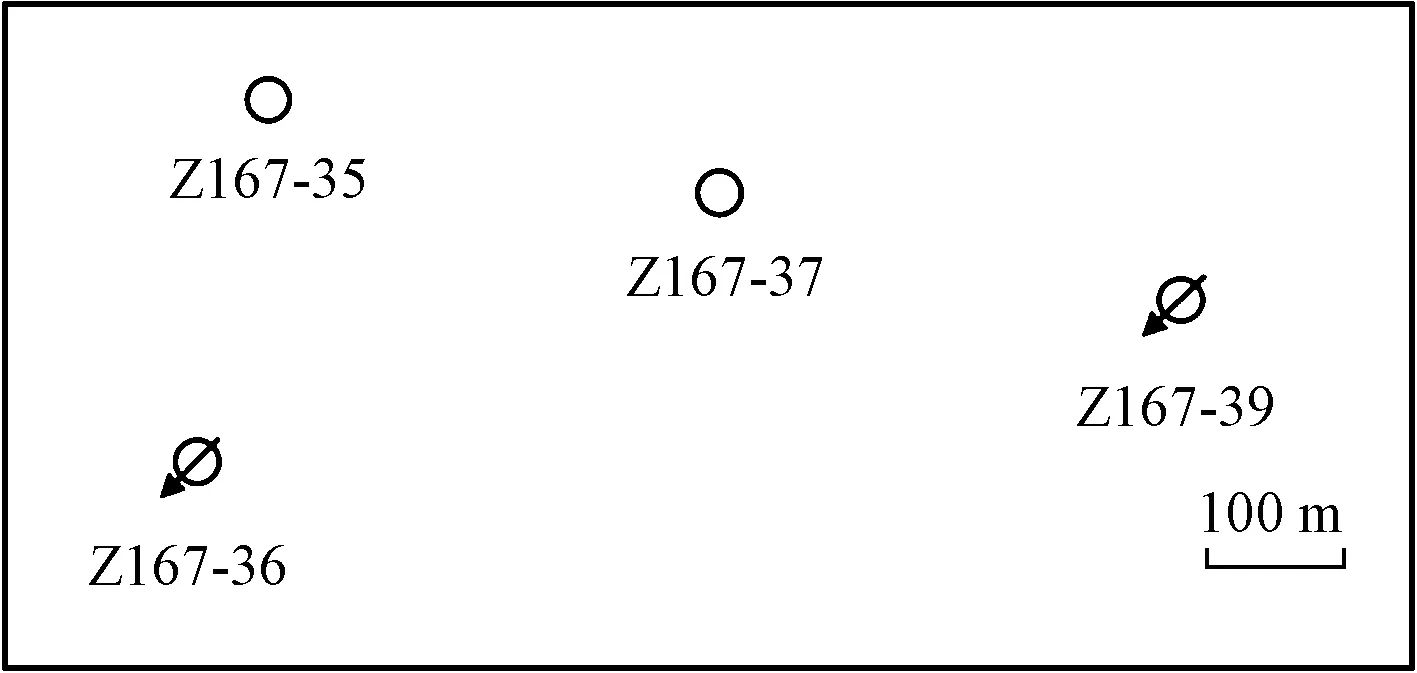
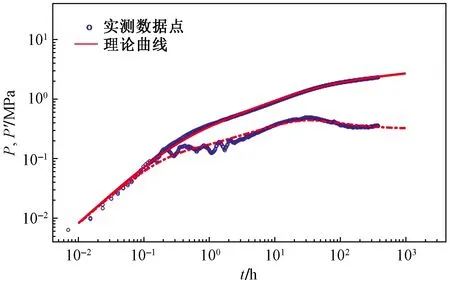
0 (4) -1 (5) 在裂缝壁面上,裂缝压力与油层压力相等,即 (6) 将观察井压裂缝分成2n等份,干扰井压裂缝分成2m等份,如图2所示。为了使后文描述更加方便,将每条裂缝分成2部分,即观察井压裂缝AB分为OA缝和OB缝,干扰井压裂缝A′B′分为O′A′缝和O′B′缝。 图2 压裂缝有限差分示意图 在观察井每一条半缝第j个单元上,其积分方程可以表达为 (7) (8) 流量积分方程可以写为 0 (9) -1 (10) 干扰井井底压力的表达式为 0 (11) -CxfD (12) 在干扰井裂缝壁面上,裂缝压力与油层压力相等,即 (13) 干扰井裂缝分成2m等份,在每一条半缝的第j个单元上,其积分方程可以表达为 (14) (15) 流量积分方程可以写为 0 (16) -CxfD (17) 另外,考虑观察井和干扰井裂缝单元的流量归一化方程,有 (18) (19) 将式(18)和式(19)分别按照观察井和干扰井裂缝单元离散化,得到 (20) (21) 采用Newton-Raphson迭代法求解方程组,根据Stephfest数值反演方法,通过商业软件平台编写计算程序,得到观察井无量纲井底压力,在双对数坐标系上绘制出典型曲线(图3)。 图3 存在压裂井干扰的压裂井试井曲线 典型曲线分为6个流动阶段:第Ⅰ阶段为井筒存储效应和表皮效应作用的续流段;第Ⅱ阶段为有限导流垂直裂缝影响的双线性流阶段;第Ⅲ阶段为地层向裂缝流动的线性流阶段;第Ⅳ阶段为系统拟径向流阶段;第Ⅴ阶段为干扰过渡阶段,此时干扰井干扰信号传导至观察井井底,压力导数曲线不再保持水平,干扰井为注水井时,压力导数曲线呈现下掉趋势,干扰井为油井时,压力导数曲线呈现上升趋势;第Ⅵ阶段为干扰径向流阶段,干扰井压力变化达到拟稳定状态,压力导数曲线趋于水平,其值等于0.5(1+qD)。 在干扰井压力信号到达前,观察井两段裂缝表面线流量对称分布,如图4(a)所示,横坐标为无量纲距离,纵坐标为裂缝表面无量纲线流量,x正半轴代表了OA缝,x负半轴代表了OB缝,原点代表了井筒的位置。当无量纲时间tD较小时,仅在井筒附近形成了压力漏斗,近井端裂缝压力降大,远井端裂缝压力降小,表现出近井端裂缝无量纲线流量大,远井端裂缝无量纲线流量小。随着时间推移,地层流体向裂缝流动,远井端裂缝无量纲线流量逐渐增大,由于观察井定产量生产,近井端裂缝无量纲线流量相对地逐渐减小,形成近井端和远井端裂缝无量纲线流量都较大,而裂缝中部无量纲线流量较小的“U”形分布。同理,在观察井压力信号到达前,干扰井裂缝表面线流量分布规律与观察井类似,如图4(b)所示。 图4 在不同tD下观察井和干扰井裂缝表面流量分布 当干扰井压力信号传导到压裂井井底时,裂缝面无量纲线流量将不再对称分布,假定干扰井是采油井,井间方位角θ=45°,位于图1中第一象限内,观察井裂缝面无量纲线流量分布如图5(a)所示,无量纲时间tD较大时,裂缝面无量纲线流量随时间的变化幅度很小,且半裂缝流量分布曲线呈现为“U”形。由于存在邻近油井干扰作用,在靠近干扰井的半条裂缝(即OA缝)表面无量纲线流量将会减小,由于观察井定产量生产,则远离干扰井的半条裂缝(即OB缝)表面无量纲线流量将会相对地增加,此时整个裂缝表面无量纲线流量将不再保持对称分布,而是呈现出在裂缝对称位置上,OA缝的无量纲线流量小于OB缝无量纲线流量。这种特点在裂缝的两端位置上(xD=1和xD=-1两处)表现最为明显。同理,当观察井压力信号传导到干扰井井底时,在干扰井裂缝表面无量纲线流量也呈非对称分布,且O′B′缝的无量纲线流量小于O′A′缝无量纲线流量,如图5(b)所示。 图5 不同tD下受到干扰后观察井和干扰井裂缝线流量分布 若干扰井是油井,改变干扰井无量纲产量,其他参数保持恒定,分析干扰井无量纲产量对双对数曲线的影响,如图6所示。由于前4个阶段未体现出干扰井的干扰影响,试井曲线完全重合,在干扰阶段,压力曲线和压力导数曲线皆出现上翘,且无量纲产量越大,上翘程度也就越大。若干扰井是注水井(图7),当干扰信号传导至观察井井底,压力导数曲线会出现下掉,如果注水井注水量大于或等于采油井产油量,即qD≤-1,压力导数曲线将迅速下掉至0。 图6 压裂油井无量纲产量影响对比 图7 压裂注水井无量纲注水量影响对比 考虑到干扰井和观察井布井方位变化,分析其井间方位角对试井曲线的影响(图8)。其中,观察井裂缝半长xf1=60 m,干扰井裂缝半长xf2=80 m,两井间距L=210 m(即LD=3.5)。相比于未压裂井干扰的模型,在压裂井干扰的模型中,当LD>2时,也能观察到井间方位角变化带来的影响,说明存在压裂井干扰的模型中井间方位角的影响作用更加敏感。当θ=0°左右时,两条裂缝几乎在一条直线上,由于裂缝高导压能力作用,其敏感性将达到最大。随着井间方位角θ减小,裂缝高导压能力使得干扰井压力信号将更快到达观察井井底。 图8 井间方位角影响对比 当干扰井向地层传导干扰信号时,由于压裂缝作为一个高导压通道,干扰信号必然会通过裂缝迅速传导至井底。将考虑压裂缝对干扰信号高传导作用的试井分析模型与常规模型相对比(图9)。显然,由于裂缝的高传导作用,干扰井的压力信号更早到达观察井井底,压力导数曲线也就更早偏离,出现下掉的现象。且井间方位角θ=0°时,即干扰井位于裂缝延伸方向上,将能更加明显地体现出裂缝的高传导作用,使得干扰井信号更早地传播到测试井井底,其压力导数曲线将会更早地出现下掉,反之,当井间方位角θ=90°时,即干扰井位于裂缝的垂直平分线上,这样的井位分布极大地限制了裂缝对干扰压力信号的高传导作用,考虑压裂缝对干扰信号传导影响与不考虑其影响两者模型间的试井曲线差异很小,此时难以体现裂缝对干扰信号的作用。 图9 裂缝高传导性影响对比 保持其他参数恒定,改变两井间距,观察试井曲线变化规律(图10)。随着两井距离越近,干扰井干扰信号将会越早到达观察井井底,在试井曲线上体现为干扰过渡阶段将会提前出现,压力曲线上升变缓,压力导数曲线将更早出现下掉现象。在干扰径向流阶段,压力导数曲线都将变为纵向截距为0.5(1+qD)水平线。 图10 井间距离影响对比 本模型引入了新的无量纲量裂缝半长比,用CxfD表示,其表示干扰井裂缝半长与观察井裂缝半长的比值。通过确定观察井裂缝半长和无量纲裂缝半长比两个参数,便可计算干扰井裂缝半长大小。采用控制变量法,改变裂缝半长比,分析其对试井曲线的敏感性。考虑到井间方位角的影响,分别假定θ=0°和θ=90°,即两井裂缝在一条直线上以及裂缝方向与布井方向垂直两种情况(图11)。当θ=0°即压裂缝分布在一条直线上时,裂缝半长比影响较为明显。且裂缝半长比越大,干扰过渡阶段将提前出现,压力导数曲线提前出线下掉。而θ=90°即裂缝方向与布井方向垂直时,裂缝半长比影响较弱。 图11 裂缝半长比影响对比 考虑观察井和干扰井裂缝的导流能力不一致,本节拟讨论干扰井裂缝导流能力对试井曲线影响。由上节内容可以推测出,当两井压裂缝在同一直线上时,裂缝的导压作用将发挥到最大,于是不妨先假定井间方位角θ=0°,以最大化干扰井裂缝导流能力的影响。依次将干扰井裂缝无量纲导流系数CFD2分别取值0.1、1、50,绘制出双对数曲线,如图12所示。当干扰井裂缝无量纲导流系数呈现数10倍量级增加时,压力导数曲线仅存在微小变化,而压力曲线间几乎看不出差异,即干扰井无量纲导流系数对双对数曲线的影响很弱。 图12 干扰井裂缝导流能力影响对比 下面采用某商用软件数值试井模块,验证模型的正确性。 利用某商用软件数值试井模块,计算压裂井干扰下的观察井井底压力,绘制在双对数曲线上,与本文所述的干扰模型曲线相对比,分析二者的吻合程度。 在数值试井模型中,一口观察井位于坐标原点,干扰井距观察井250 m,采用PEBI网格离散整个油藏,如图13所示,两压裂井以及油藏的基本参数则如表1所示。 表1 两压裂井和油藏基础参数 干扰井和观察井都作为生产井生产,图13表示两压裂井附近地层的压力展布。通过数值试井计算,得到观察井井底压力。 图13 压裂井和压裂井作用下的压力分布 处理数值试井模拟所得到的观察井井底压力资料,计算出压力和压力导数随时间的变化关系,绘制在双对数坐标系上,分别用本文的压裂井邻井干扰模型和常规单井模型解释(图14)。显然压裂井邻井干扰模型能够更加有效解释压力曲线和压力导数曲线后期上翘的特征,更好拟合存在邻井干扰的压力数据。 图14 邻井干扰模型与单井模型拟合效果对比 Z167-37井位于HS油田Z36区块,油层中深1 895.6 m,地层有效厚度11 m,孔隙度为12.66%,综合压缩系数为1.496×10-3MPa-1,原油黏度为1.32 mPa·s,体积系数为1.26。该井于2018年4月进行井下关井压力恢复测试,关井前产液量为1.15 m3/d,综合含水率为8.4%。 Z167-37井附近有3口井(图15),其中油井1口,注水井2口。该井含水率长期保持在10%左右,日产液量也较低,注水不见效。关井380 h,对压力恢复资料处理分析,绘制在双对数坐标系上(图16)。压力导数曲线后期下掉并最终趋于水平,认为是附近油井Z167-35井干扰所致。两井间距286 m,Z167-35井产液量为0.89 m3/d。利用本文所建模型解释,解释结果参数如表2所示,解释干扰井流量为0.82 m3/d,与Z167-35井的日产液量相近,证明Z167-37井所受干扰的确来自Z167-35井。 图15 Z167-37井与其邻井井位关系 图16 Z167-37井拟合曲线 表2 Z167-37井解释结果参数 (1)建立了存在压裂井干扰条件下,有限导流压裂井邻井干扰试井分析模型,考虑了观察井和干扰井裂缝相互干扰的影响,分析了裂缝流量不对称的现象。绘制压力和压力导数典型曲线,典型曲线出现了干扰过渡段和干扰拟径向流段。 (2)分析了观察井和干扰井裂缝表面无量纲线流量分布规律,当干扰信号到达观察井时,观察井裂缝表面线流量将非对称分布,其大小变化将根据干扰井的位置和注采工作制度所决定。当井间方位角等于0°时,即两压裂井压裂缝位于同一直线上,裂缝高导压作用将会到达到最大,干扰井压力信号将会更快到达观察井,压力导数曲线将提前出现干扰过渡段。 (3)利用某商业软件数值试井模拟功能,验证了本文模型的正确性。将本文模型应用到压裂井实测资料解释中,解释结果不仅能说明压力导数曲线后期异常的现象,得到更加合理的解释参数,而且可以初步判断测试井与邻井的连通状况。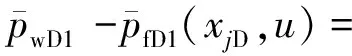

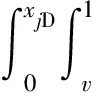
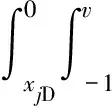
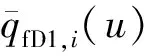
1.3 干扰井裂缝模型
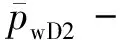
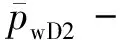
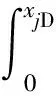

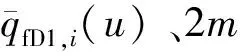

2 典型试井曲线分析
2.1 裂缝表面线流量分布规律


2.2 干扰井无量纲注/采量的影响

2.3 井间方位角的影响
2.4 裂缝高传导性的影响
2.5 井间距离的影响
2.6 干扰井裂缝半长的影响
2.7 干扰井裂缝导流能力的影响
3 数值验证及实际应用
3.1 数值试井方法验证

3.2 实例解释

4 结论
