概率法在煤层气储量估算中的应用

张晨朔，韩 征，冯志刚，张道勇

(自然资源部油气资源战略研究中心，北京 100034)

储量评价是一项贯穿于油气勘探开发过程中的重要内容。油气储量估算方法分为容/体积法、动态法、类比法和概率法等[1-2]，其中容/体积法对各项储量参数综合评估，进行确定性取值，再代入计算公式求取储量，适用于勘探开发的不同阶段；动态法依据油气藏开发过程中的压力、产量等生产参数，运用物质平衡等方法求取储量，一般适用于具备了较为丰富的生产动态资料、处于开发中后期的油气藏；类比法通常适用于远景储量估算，准确度较低；概率法与容/体积法原理类似，可以认为是容/体积法的一种延伸，但估算参数取值存在变化范围，最终储量估算结果以累积概率的形式呈现，适用于储层条件复杂、参数尚不确定的情况。

煤层气具有特殊的地质条件，其赋存、运移规律及动力学模式均有别于常规石油天然气[3-4]。处于储量评价初期的煤层气藏，存在地质资料少、储量估算参数不明确、储量认知程度低的问题[5]，使用体积法不容易全面客观地对储量进行评价。另外尚未开发的煤层气藏，也无法使用动态法。针对此类情形，使用概率法不仅可以根据储量参数样本，求得储量所在范围，而且还可以给出不同概率级别下的储量估值，为储量风险评估及下一步的勘探开发决策提供参考。

以往关于概率法在油气储量估算的研究和应用主要集中在常规油气和页岩气矿藏。其中，李洁梅等[6]估算了CLFS项目中一背斜油藏的储量参数及储量的概率分布；李定军[7]针对CD气田将储量估算参数作了一定合并，再估算得到储量的概率分布；张玲等[8]针对页岩气储量参数、储量估算结果不确定性大的情况，采用概率法估算储量并分析了储量期望的置信区间及波动率；涂乙等[9-10]利用K-S检验等多种方法对储量参数的概率分布模型进行检验和优选并引入形状因子减小构造形状对储量估算的影响；谢寅符等[11]讨论了概率法与确定法的差异以及概率函数形态对估算结果的影响，指出概率法的适用性和函数选取方法。在煤层气资源储量估算方面，陈玉华等[12]将蒙特卡罗方法引入煤层气资源量计算中，论述了算法和函数实现，并应用于实例研究；刘道信[13]运用概率法估算煤层气储量，在实例中认定储层有效厚度服从均匀分布，含气量符合三角分布，通过蒙特卡罗法得到估算储量的逆累积概率曲线；郭明涛等[14]基于蒙特卡罗法估算煤层气资源量，以中梁山南矿k1急倾斜煤层为例，分析拟合煤层气储层面积服从伽马分布，厚度服从对数正态分布，含气量满足Beta PERT分布，进而利用体积法公式迭代计算出煤层气资源量的概率分布情况。目前概率法在煤层气储量估算的应用中，多采用理论模型拟合样本并估算储量，少有同时运用理论分布模型和任意分布模型估算储量的文献报道，尤其是与理论分布模型相比，利用任意分布模型拟合参数样本得到的储量估算结果具有何种精度和特点仍不清晰。为此，针对处于评价阶段的M煤层气藏，基于已取得的储量估算参数样本(储层面积、厚度及含气量)，结合煤层气储量参数特点建立相应的概率分布模型，主要包括理论分布(三角分布、正态分布、对数正态分布、威布尔分布、伽马分布)及任意分布；利用Kolmogorov-Smirnov(K-S)、卡方检验对相关理论模型进行优选并提出不同模型的组合方案；运用蒙特卡罗方法按各方案进行储量估算，得到储量概率分布，并分析了理论分布模型和任意分布模型对储量估算结果的影响特征，从而达到全面客观评估储量以及降低决策风险的目的。

1 概率法原理及模型

对煤层气储量的估算，概率法与体积法具有相同的公式[15]，即

Gi=0.01AhDCad

(1)

式(1)中：Gi为煤层气地质储量，108m3；A为煤层含气面积，km2；h为煤层净厚度，m；D为煤的空气干燥基视密度(煤的容重)，t/m3；Cad为煤的空气干燥基含气量，m3/t。

与体积法不同的是，概率法的储量估算参数是满足某些概率分布的随机变量，可以在一定范围内取值，从而储量也是各项参数变量的积，也存在相应的置信区间[16]。储量估算结果一般采用蒙特卡罗方法求得[17-18]，由逆累积概率分布曲线表示，并给出不同概率级别下的储量估值。在实践中，通常以逆累积概率10%(P10)、50%(P50)、90%(P90)的对应值表示储量或估算参数落实程度的低值、中值、高值。

储量估算参数的样本可由特定的概率分布模型来拟合。概率法估算油气储量常用的概率分布模型有理论分布和任意分布。其中理论分布模型有特定的函数表达式，包括均匀分布、三角分布、正态分布、对数正态分布，威布尔分布和伽马分布等。当参数只能获得一个范围值，并且在该范围内均匀分布时通常满足均匀分布模型。当参数不仅存在范围值，还存在最可能值时，可以采用三角分布来描述。三角分布一般适用于描述储层面积和厚度，但由于概率密度为线性分布，可能存在对尾数估计过高的情况。正态分布、对数正态分布，威布尔分布、伽马分布在油气储量估算领域较为常见，通常用来描述储层面积、厚度、孔隙度、饱和度等参数。任意分布模型，又称频率统计法或经验分布法，即不采用特定函数描述参数样本分布，而是通过把样本划分到n个区间，统计各区间的频数与频率，从而获得参数的概率密度分布及累积概率分布。任意分布适用于样本分布规律不明显以及数量较大的情况。

常用理论分布模型的概率密度函数如下。

(1)均匀分布：

(2)

式(2)中：a、b为分布区间的边界值。

(2)三角分布：

(3)

式(3)中：c为众数。

(3)正态分布：

(4)

式(4)中：μ为x的期望；σ为x的标准差。

(4)对数正态分布：

(5)

(5)威布尔分布：

(6)

式(6)中：α、β为分布调整参数。

(6)伽马分布：

(7)

2 实例应用

M煤层气藏位于N盆地南部向西北倾的斜坡带上，地质构造简单，断层稀少，主要以褶皱为主，褶皱为宽缓的背斜和向斜。储层为二叠系下统山西组地层，煤层倾角小，煤层底板起伏幅度小，标高变化不大，煤层厚度变化在4～8 m，整体趋势西低东高。煤类属腐植型无烟煤，煤岩成分以亮煤和暗煤为主。储层含气量为9～25 m3/t，整体表现出两边高中间低的趋势。在该实例应用中，需要重点分析的储量估算参数有储层面积、储层厚度及储层含气量。

2.1 储层面积

M煤层气藏地质构造简单，断层较少，经过勘探评价含气面积比较落实，存在最大可能估计值，适合采用三角分布和正态分布模型。首先根据前期勘探及相关地质研究确定M煤层气藏的期望含气面积，即P50对应值为17.60 km2，以P50面积为基准，上下各浮动0.60 km2作为P10和P90，因此P10对应值为18.20 km2，P90对应值为17.00 km2。

根据P50、P10和P90对应含气面积分别确定三角分布和正态分布的函数参数：对于三角分布，参数a=16.72，b=18.48，c=17.60；对于正态分布，参数μ=17.60，σ=0.47。由此绘制出在三角分布和正态分布模型下的储层面积的概率密度和逆累积概率分布曲线(图1、图2)。

由图1可以看出，在概率密度曲线形态上，正态分布较为低宽，三角分布较为高窄。在P50对应的17.60 km2储层面积附近三角分布的概率密度要大于正态分布；当储层面积小于17.00 km2或者大于18.20 km2时，正态分布的概率密度大于三角分布；在a点和b点，即储层面积为16.72 km2和18.48 km2时，三角分布的概率密度为0，而正态分布在超出a点和b点后仍具有一定的概率分布，直至16.00 km2和19.00 km2附近。由图2可以看出，正态分布的逆累积概率分布曲线更为平缓，在储层面积大于18.50 km2时仍有一定的概率可能性。因此，采用P50、P10、P90建立三角分布和正态分布模型时，正态分布模型具有更大概率分布区间以及更为平缓的概率密度，此种差异对储量结果的影响应加以考虑。

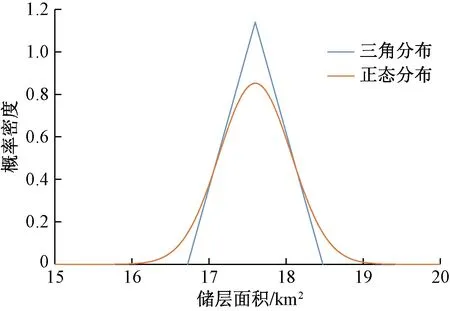
图1 储层面积的概率密度曲线

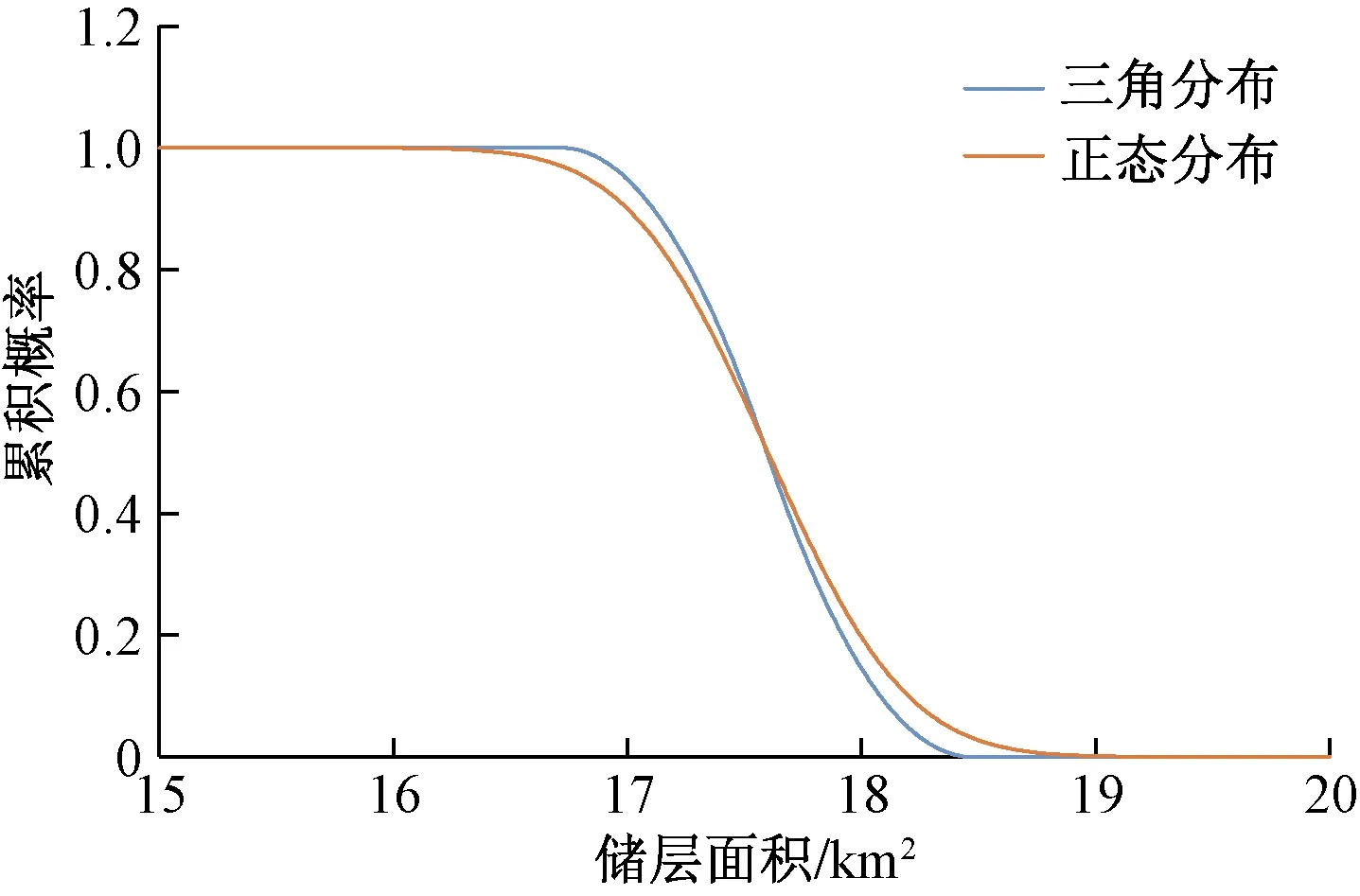
图2 储层面积的逆累积概率曲线

2.2 储层厚度

该煤层气藏储层发育比较稳定，储层厚度由钻孔取样获得，共98个样本，分布区间为4.14～7.22 m，分50组统计频数及频率，概率分布如图3、图4所示。储层厚度样本数量较大，为全面分析、对比评价不同方法对储量估算结果的影响，分别采用理论分布模型和任意分布模型拟合样本。

2.2.1 理论分布模型

选取正态分布、对数正态分布、威布尔分布和伽马分布函数，分别对储层厚度样本进行拟合，得到函数分布参数；对样本拟合优度进行K-S检验和卡方检验；估算各函数的逆累积概率P10、P50、P90对应的储层厚度，数据如表1所示。绘制4个分布函数模型下的储层厚度的概率密度曲线和逆累积概率曲线(图3、图4)。

表1 储层厚度的理论分布模型数据

由图3、图4可以看出，理论分布模型的概率分布曲线比样本分布平缓；各函数的概率分布相差不大，均能较好地拟合原始样本，反映实际情况。4个分布函数中P10对应的储层厚度为6.64～6.70 m，P50对应的储层厚度为6.05～6.12 m，P90对应的储层厚度为5.39～5.48 m。经过K-S检验和卡方检验，威布尔分布的P最接近1，对样本具有更高的拟合度。

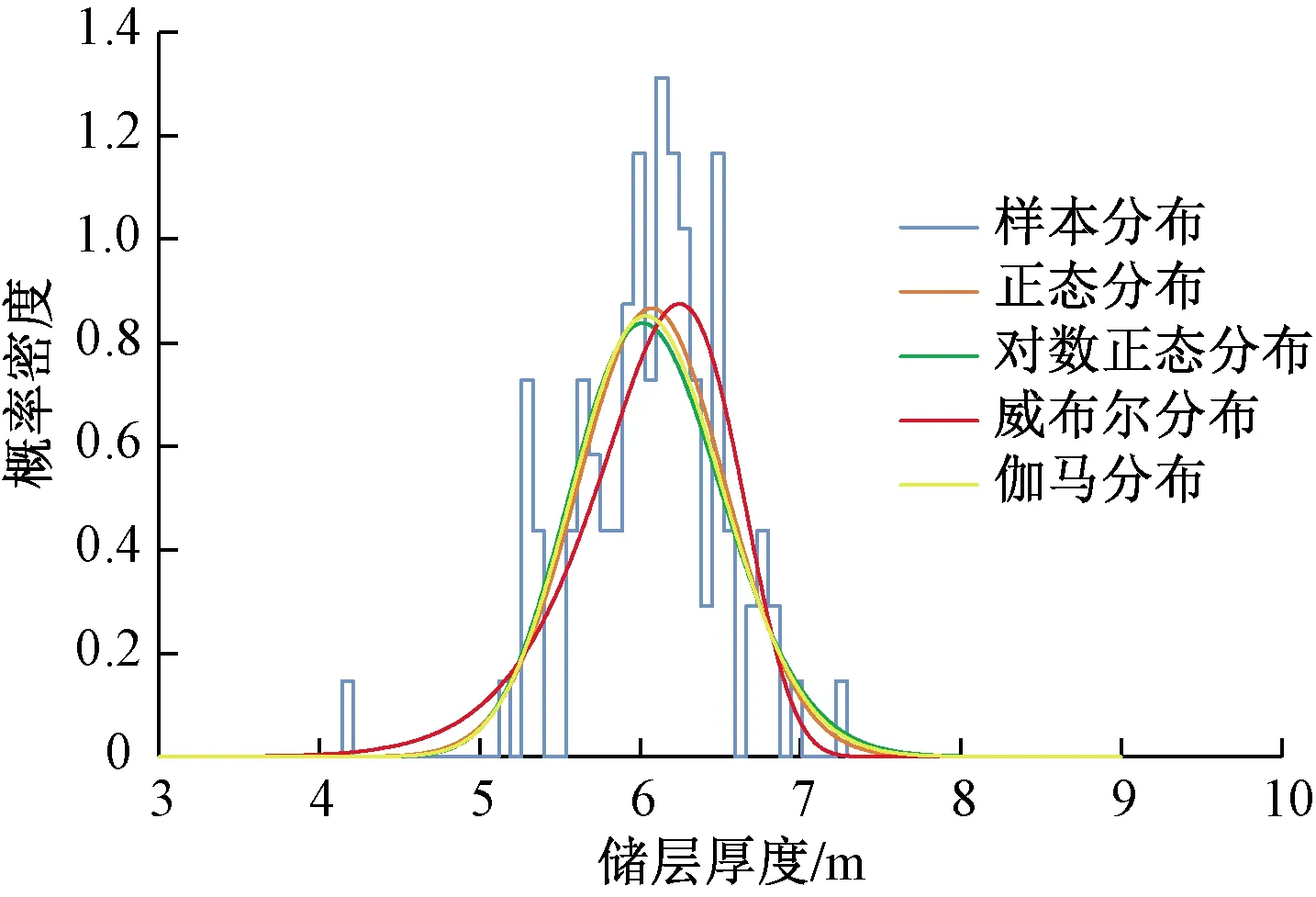
图3 储层厚度的概率密度曲线

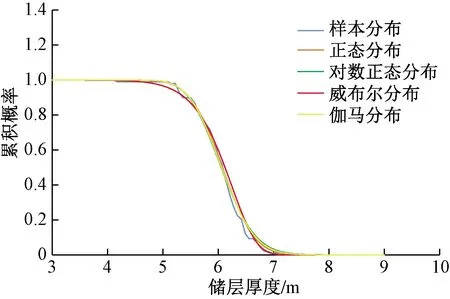
图4 储层厚度的逆累积概率曲线

2.2.2 任意分布模型

根据样本分组得到各组的频数及频率，在各组区间采取均匀分布方法随机产生模拟样本，各组区间内的模拟样本数量服从原有频率，从而生成关于储层厚度的模拟样本库。模拟样本库概率分布和逆累积分布如图5所示。由图5可以看出，在任意分布情形下，虽然增加了模拟样本数量，但概率密度和累积概率分布的趋势均服从原始样本分布规律。由逆累积概率曲线可以得到P10、P50、P90对应的储层厚度分别为6.55、6.11、5.38 m，与理论分布模型的4个函数估算值相近。其中P10对应的储层厚度略小，这是因为任意分布的概率分布区间更具体并且更窄。

图5 储层厚度的任意分布概率曲线

2.3 储层含气量

储层含气量主要与煤阶、镜质组含量、灰分、以及储层温度和压力相关。M煤层气藏煤层埋深250～700 m，地层压力在0.96～2.47 MPa，压力梯度在0.153～0.563 MPa/100 m，平均为0.38 MPa/100 m，处于欠压状态。地层温度约为21.0 ℃(270.7～276.0 m)，地温梯度较低，为2 ℃/100 m。储层条件下兰格缪尔体积介于39.94～46.38 m3/t，平均42.91 m3/t，兰格缪尔压力为2.69～3.22 MPa，平均2.93 MPa。通过煤层钻孔和实验可以获得储层含气量。含气量共54个样本，分布区间为9.73～24.49 m3/t，分20组统计频数及频率，概率分布如图6、图7所示。与储层厚度类似，储层含气量也采用理论分布模型和任意分布模型对样本进行拟合。

2.3.1 理论分布模型

选取正态分布、对数正态分布、威布尔分布和伽马分布函数，分别对储层含气量样本进行拟合和检验，并估算逆累积概率P10、P50、P90对应的储层含气量，数据如表2所示。绘制4个分布函数模型下的储层厚度的概率密度曲线和逆累积概率曲线(图6、图7)。

表2 储层含气量的理论分布模型数据

由图6、图7可以看出，各函数的概率分布有一定的差别，其中对数正态分布的概率密度曲线和伽马分布较为接近，而正态分布和威布尔分布的峰值有所右偏。4个分布函数中P10对应的储层含气量为21.74～22.01 m3/t，P50对应的储层含气量为17.05～17.59 m3/t，P90对应的储层含气量为12.54～13.21 m3/t。经过K-S检验和卡方检验，伽马分布与对数正态分布的拟合较好，其中伽马分布的P最接近1，对样本具有更高的拟合度。

图6 储层含气量的概率密度曲线

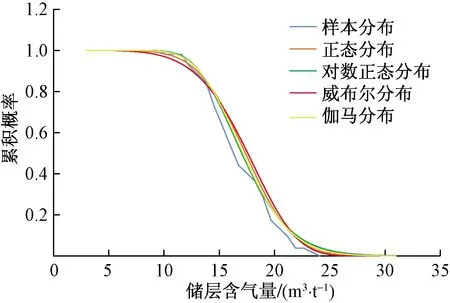
图7 储层含气量的逆累积概率曲线

2.3.2 任意分布模型

与储层厚度任意分布方法相同，根据样本分组得到各组的频数及频率，在各组区间采取均匀分布方法随机产生模拟样本，各组区间内的模拟样本数量服从原有频率，从而生成关于储层含气量的模拟样本库。模拟样本库概率分布和逆累积分布如图8所示。由图8可以看出，在任意分布情形下，概率密度和累积概率分布的趋势均服从原始样本分布规律。由逆累积概率曲线可以得到P10、P50、P90对应的储层含气量分别为21.61、16.59 m、13.05 m3/t，与理论函数模型的4个函数估算值相近，其中P50对应的储层含气量略小。

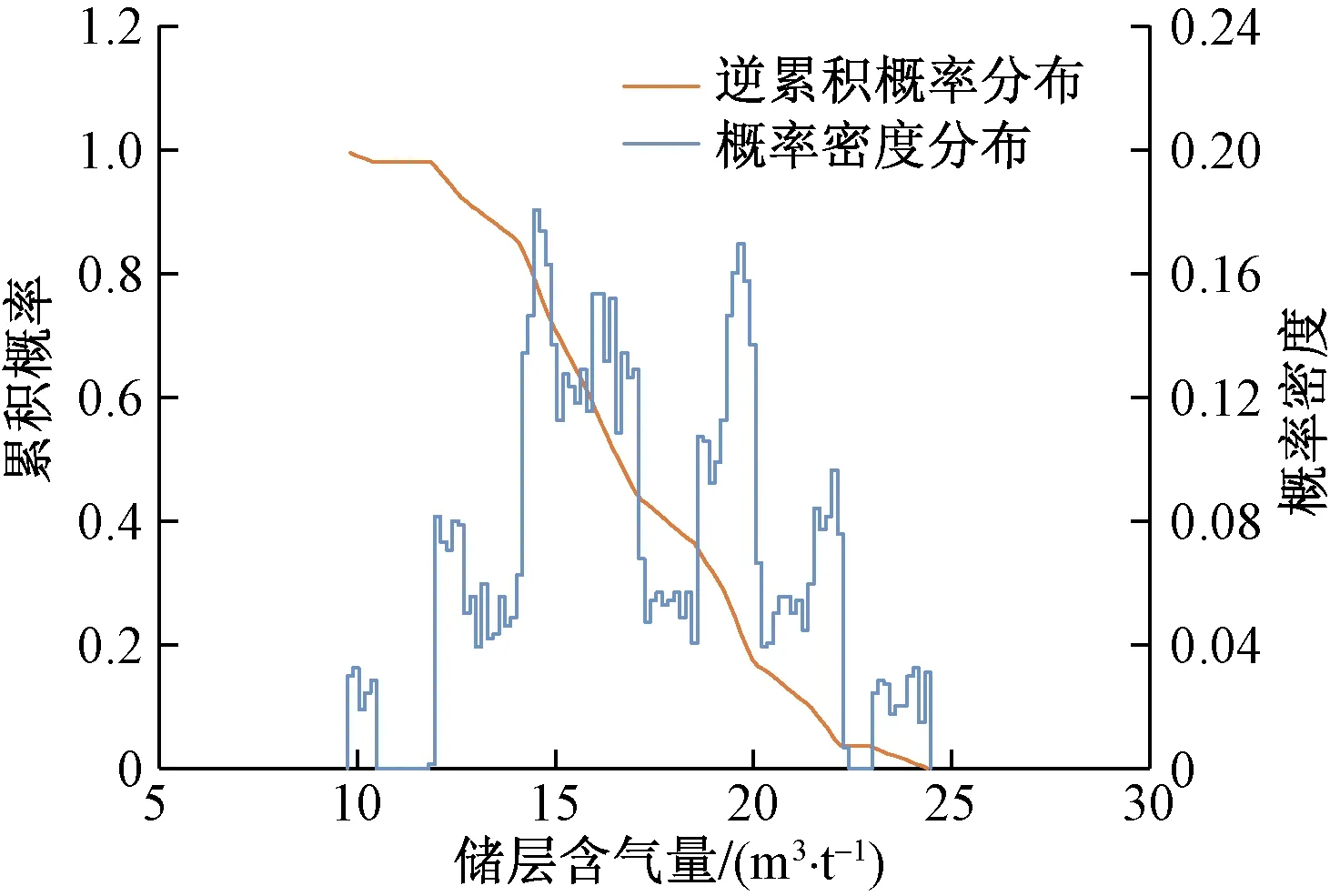
图8 储层含气量的任意分布概率曲线

2.4 储量估算

储量估算采用蒙特卡罗方法，从储量参数中随机抽取数据并代入煤层气储量公式计算，重复过程直到获得足够多的储量估算数值。其中各项储量参数数据均符合一定分布规律。在煤层气储量估算参数中，煤的容重相对恒定，这里可以取常数1.46 t/m3，储层面积、厚度及含气量参数分别采用多种概率方法估算。根据各参数采用不同概率方法的组合，形成4个组合方案：①储层面积采用三角分布，储层厚度采用威布尔分布，储层含气量采用伽马分布；②储层面积采用三角分布，储层厚度采用任意分布，储层含气量采用任意分布；③储层面积采用正态分布，储层厚度采用威布尔分布，储层含气量采用伽马分布；④储层面积采用正态分布，储层厚度采用任意分布，储层含气量采用任意分布。

在此基础上，按各方案方法每组均重复5 000次随机计算，获得5 000个储量估算数值，分100组统计频数及频率。概率密度曲线及逆累积概率曲线如图9所示，储量估算结果如表3所示。

由图9、表3可知，4组方案的储量估算结果均相差不大，其中P10对应的储量为33.76～34.73×108m3，P50对应的储量为25.91～26.54×108m3，P90对应的储量为19.44～20.11×108m3，储量平均值为26.64～27.14×108m3。该煤层气藏利用体积法估算储量为27.41×108m3，与方案①的储量平均值Pmean的27.14×108m3最为接近。

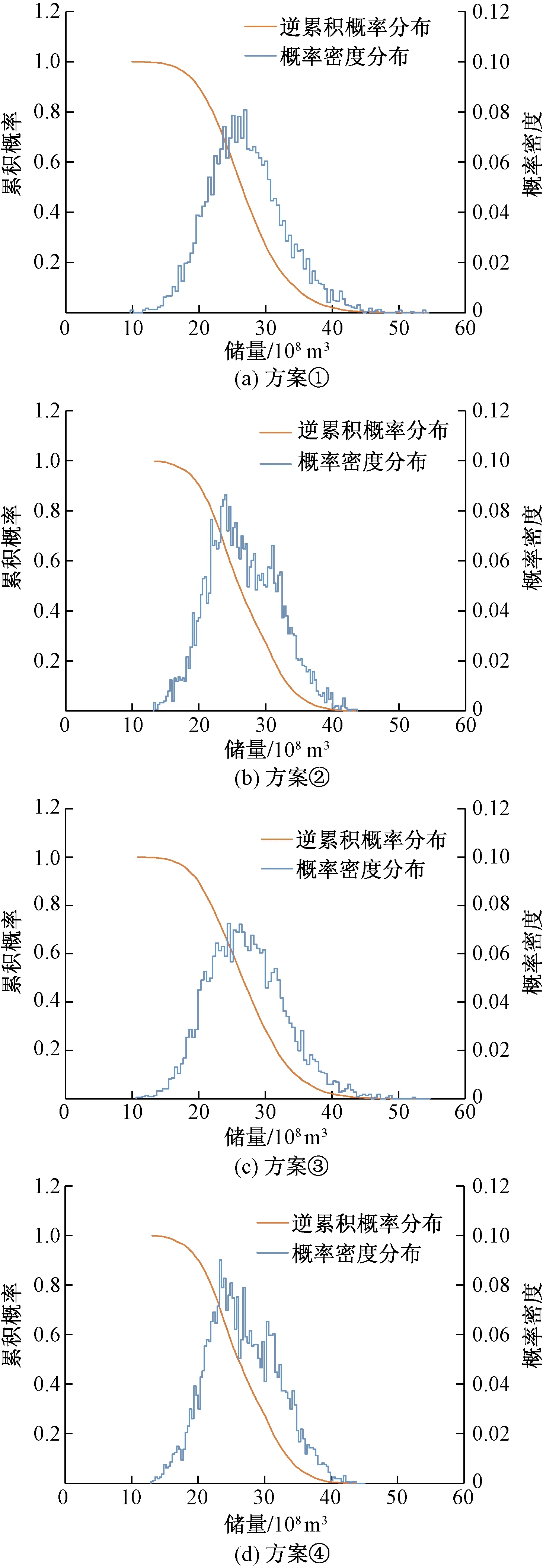
图9 各方案的储量概率曲线

表3 概率法煤层气藏储量估算值

方案①、③同方案②、④相比，方案①、③的储量数值分布区间在10×108～50×108m3附近，而方案②、④的储量数值分布区间在13～45×108m3附近，说明储层厚度与含气量采用任意分布的概率分布区间较窄，导致储量的概率分布也相对较窄。类似的，方案①、③的P10对应的储量大于方案②、④，而方案①、③的P90对应的储量小于方案②、④，也说明了采用任意分布时的概率分布区间较窄，储量的概率分布也较为集中。方案①、③的概率密度曲线整体起伏变化较小，逆累积概率曲线也更加平滑，说明方案①、③采用理论分布函数拟合对原始样本分布呈现出了过滤效果。另外从各个级别的储量数据对比看，方案①和方案③的储量结果相近，而方案②和方案④的储量结果相近。这是由于储层厚度及含气量的置信区间较宽，尤其是含气量的P10/P90达到1.65(储层厚度的P10/P90为1.23，储层面积的P10/P90为1.07)，因此当储层厚度及含气量采用理论分布模型和任意分布模型两种不同方法时，对储量估算结果存在一定影响。

方案①同方案③相比，概率密度曲线峰值更高，体现了储层面积采用三角分布对储量估算结果的影响。但由于储层面积相较于储层厚度及含气量，储层面积的置信区间较窄，对储量估算结果的影响也有限，因此，两个方案的结果比较相近。

3 结论

(1)概率法估算煤层气储量，如果储量估算参数存在最大可能估计值，可以利用P50、P10、P90建立三角分布、正态分布等模型，但需要考虑三角分布与正态分布概率区间对储量的影响。

(2)在煤层气储量估算参数中，储层含气量受煤级、温度和压力的影响，样本数值差异可能较大，通常是对储量估算结果影响较大的参数。

(3)当储量估算参数样本数量较大时，可以同时采用理论分布模型和任意分布模型，其中任意分布模型以及在其基础上估算得到的储量结果的置信区间较窄，体现了原始样本分布的规律；而理论分布模型由于其对原始样本分布的过滤作用，得到的概率分布更加平滑。在实际应用中，应根据各参数采用不同模型方法分组估算储量，通过对比分析分组结果或取平均值确定目标煤层气藏各概率级别下的储量数值。