一种基于功率谱的多载波信号频率、带宽提取算法①
2021-02-23崔倩,张朗,刘斌,康辉
崔 倩,张 朗,刘 斌,康 辉
(1.陕西航天技术应用研究院有限公司,西安 710071;2.中国空间技术研究院西安分院,西安 710000)
0 引言
为了及时发现卫通信道上信号突发的、不确定性的错误,需要对卫通信号开展缺乏先验知识的频谱监测研究,对卫通信号的载波频率、带宽、调制方式、信噪比等信号特征参数开展估计、分析。 卫通信号的载波频率和带宽的估计是其他信号特征参数估计的基础,其估计结果及精度直接影响调制方式[1]、信噪比的计算精度[2]。 因此,快速、准确提取卫通信号载频信息是开展卫通信号频谱监测的一项重要课题。
常用的信号频率估计方法有判决反馈估计法[3]、重心法[4]、瞬时相位法[5-6]、倍频法[7]等,重心法频率估计、锁相环法及倍频法都需要具有载波先验知识,而瞬时相位法不适合多载波信号;常用的信号带宽估计算法有自相关法、均方根法、直接法[8]和能量集中法[9],这几种方法估计的带宽精度比较低,往往不能满足实际需求。
本文提出一种基于信号功率谱图[10]的载频信息估计方法。 该方法利用Welch 算法[11-12]计算所得信号功率谱,绘制功率谱图,数据长度一定的条件下,相较于直接求得的功率谱,通过Welch 方法获得的功率谱会更加平滑,因此估计带宽和中心频率时会更加精确。
1 基于功率谱的参数估计
1.1 功率谱计算
基于Welch 的功率谱分辨率取决于每段数据的长度,而方差取决于K的大小。 在有限数据长度限制下,即N=KL,N一定,当L变大时,K就相应地变小,方差相应会变大,体现在频谱上就是毛刺变多。为了减少毛刺,提高估计精度,就必须增大K的值,那么在一定的数据量的前提下,只有重复利用数据才能增加段数K,Welch 法就是利用数据重叠来达到增加段数K的目的[13]。 重复数据长度越长,K越大,功率谱越平滑,但是每段数据独立性也变得越来越弱,画出的功率谱就会畸形。 实践证明,重叠数据长度取L/6 是比较合理的。 用到的窗函数是hamming,窗长度为L。 对多次计算的功率谱进行加权平滑[14],减小随机噪声的影响。
1.2 载波分离
第一步是对获得的功率谱进行滤波,滤除高频分量,使得功率谱曲线更加平滑,进一步保证估计结果的精度。 把获得的功率谱当作时域信息,计算功率谱,通过功率谱图可以确定滤波器的通带阻带截止频率。 滤波前后数据如图1 所示。

图1 滤波前后功率谱图Fig.1 Pre and post filtering spectrum
第二步将载波分离出来,分离载波最重要的就是确定载波的左右下角位置(载波位置由其左下角、左上角、右上角、右下角的4 个特殊点来确定),本文是通过曲率[15]来确定载波边界的,设信号功率谱为主要步骤如下:
1)对功率谱进行第一次差分运算,可以得到X2-X1,X3-X2,X4-X3…Xn-Xn-1,若差分结果为大于等于0 时记为1,结果为负数时记为0,则1,0 的连续值代表了数据的递增或者递减的规律。
2)对第一次差分得到的1,0 值进行第二次差分运算,当到达波峰时差分值变为-1,波谷差分值变为1,其余都为0。 取出1,-1 位置所对应的原始功率谱数据,其余位置率谱数据置为0,可以表示为0,Xi,0,0,0,0,0,Xj,0,0,0,0,Kk,0,0,0,Xl,0,0,0,Xt…。
3)将两个不为0 的数据所在位置中间的0 数据用后一数据值来代替,结果可表示为Xi,Xi,Xj,Xj,Xj,Xj,Xj,Xj,Xk,Xk,Xk,Xk,Xk,Xl,Xl,Xl,Xl,Xt,Xt,Xt,Xt…,功率谱图如图2 所示:
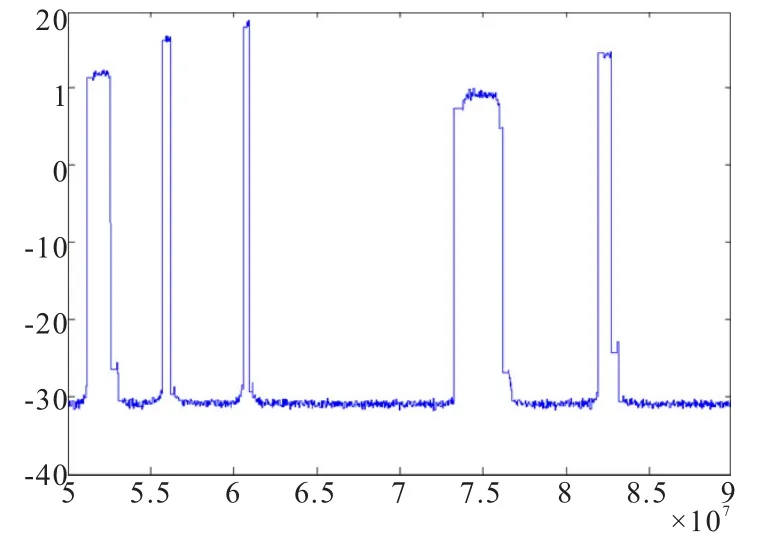
图2 处理后功率谱图Fig.2 Processed spectrum image
4)对步骤3 所得数据进行第三次差分,假设预先设置的判决门限为Δx,若有xj-xi>Δx,则我们认为此处有载波,并且认为xi对应位置为载波的左下角位置;若有xl-xk>-Δx,则认为xk对应位置为载波的右上角位置。 经过对功率谱进行一次完整的扫描后,即可得到观测窗口内各载波左下角和右上角的位置。
5)为了得到载波的左上角、右下角位置,需要进行一次反向扫描,即先将功率谱反向输出作为扫描的输入数据,则扫描结果经位置反变换后即为载波的左上角、右下角位置。 如此,可以得到载波的左右边界即左下角、右下角位置,即可初步获得载波的中心频率和带宽。
6)对于步骤3 中的数据,如果连续出现几个位置都大于门限值,则取最右边一个位置为载波左边界;如果连续出现几个位置都小于门限值,则取最左边一个位置为载波右边界,防止出现一个中心频率对应多个带宽的情况。
1.3 计算中心频率带宽
经过载波分离已经知道载波左右边界的大概位置,通过该位置我们可以得到中心频率的粗略位置。以该位置为中心,取该位置及其左右各3 个点,一共7 个点取平均即可估算出载波功率值。 从载波左右边界向外各取4 个点,一共10 个点取平均即可得到底噪位置。
设置门限,从中心频率位置开始往两边遍历,如果连续5 个点的值都下降到门限值以下,则可认为5 个点中距离中心频率最近的一个点分别为载波的左右边界位置XL和XR。 则该信号的带宽和中心频率分别为:
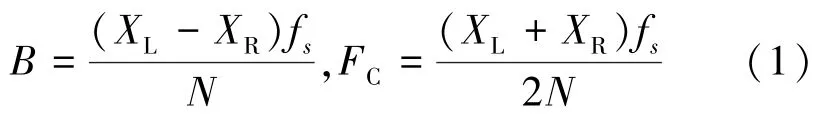
其中fs为采用频率,N为FFT 点数。
整个算法步骤如下:
1)利用Welch 估计功率谱;
2)对功率谱进行滤波,使其更加平滑;
3)通过二次差分对功率谱进行修正,并初步获得载波的左右边界位置;
4)通过修正的功率谱以及载波左右边界位置获得载波功率和底噪,然后向两边遍历直到连续5个点都下降到载波功率的1/20 处(可调整)[10],即可获得载波左右边界,进而计算带宽和中心频率。
2 实验与仿真分析
2.1 估计精度仿真分析
本文对5 种调制方式载波进行仿真,采样率250 MHz,分辨率2 kHz,SNR 的范围为1 ~31 dB,步长2 dB。 对不同的SNR 取值进行100 次仿真,计算误差,得到SNR 与中心频率和带宽的NMSE 曲线,如图3、图4 所示。
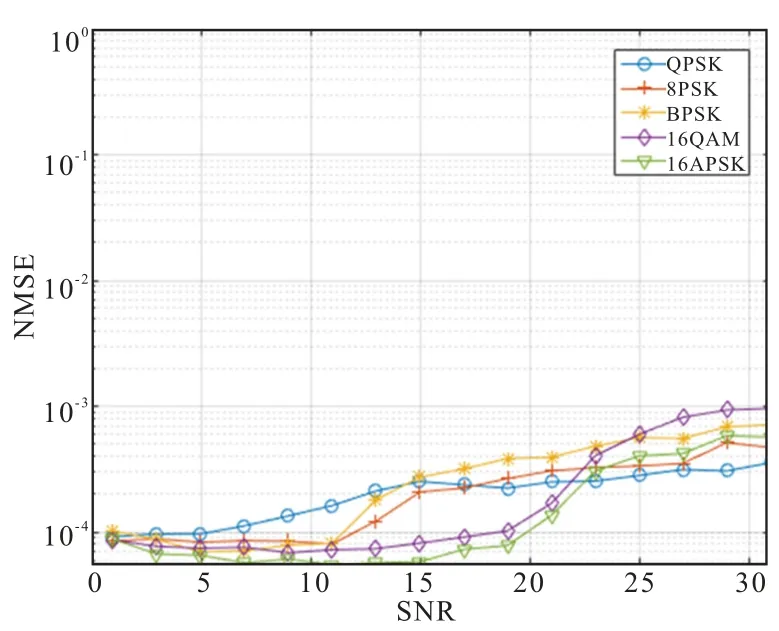
图3 频率NMSE 与SNR 关系图Fig.3 Relationship of frequency NMSE via SNR

图4 带宽NMSE 与SNR 关系图Fig.4 Relationship of bandwidth NMSE via SNR
仿真条件:采样速率250 MSPS,调制方式为BPSK、QPSK、16APSK、16QAM 和 8PSK,其中心频率分别 为 52. 07 MHz、 58. 06 MHz、 65. 85 MHz、74.88 MHz、 82. 48 MHz, 码 元 速 率 分 别为0.3 MSPS、0. 512 MSPS、1 MSPS、1. 3 MSPS、2.0 MSPS,使用系数归一化的根升余弦成型滤波器,滚降系数0.35,采用“measured”方式加噪。
2.2 处理速度仿真分析
采样率250 MHz,分辨率2 kHz,SNR 为10 dB情况下,载波个数由1 增到39 时,调制方式为QPSK的载波的频率、带宽计算所用时间,如图5 所示。

图5 载波个数与处理时间关系图Fig.5 Relationship of carrier number and processing time
从图5 可以看出,载波个数的变化对处理时间影响很小,因此该方法特别适用于多载波处理的场景。
2.3 算法比较
使用系数归一化的根升余弦成型滤波器,采用“measured”方式加噪的仿真条件下,本文提到的方法与常用的无频偏条件下的重心法和锁相环法中心频率的NMSR 和SNR 关系曲线如图6 所示。
从图6 可以看出,本文提到的方法识别精度与重心法基本一致,不如无频偏条件下的锁相环方法,但重心法与锁相环法需要载波先验信息,而本文提到的方法不需要任何载波先验信息。
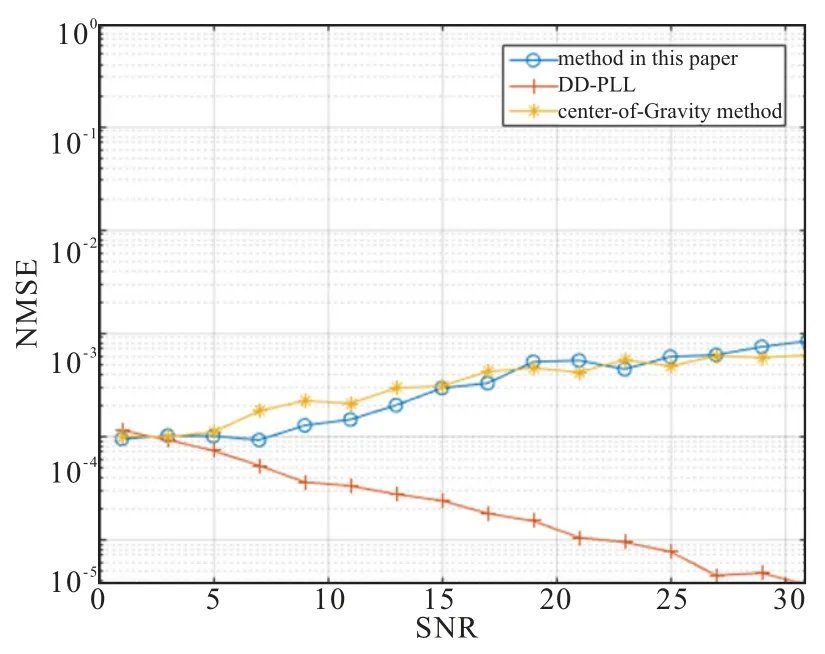
图6 不同方法与SNR 关系图Fig.6 Relationship of frequency NMSE for different method via SNR
3 结论
对于不同调制模式的卫星通信信号,本文提出的基于功率谱图的多载波中心频率及带宽估计算法,载波估计精度优4×10-4,带宽的NMSE 可达10-2量级,且在一定采样率与分辨率条件下,处理速度基本不受载波个数影响,特别适合多载波场景。
本文提到的算法已应用于XX 站频谱监视,实现了卫通网全网频率资源24 小时无缝自动监测,可及时发现卫通信道上突发的、不确定的错误,保证了用户信息的正常传输,减少了对卫星转发器的危害,避免了不必要的经济损失和不良社会影响。
