分布式控制模式下的分散式风电无功电压控制策略
2021-02-22华亮亮郭天飞张莞嘉刘其辉黄伟
华亮亮,郭天飞,张莞嘉,刘其辉,黄伟
(1.国网蒙东电力有限公司通辽供电公司,内蒙古自治区 通辽市 010010;2.华北电力大学电气与电子工程学院,北京市 昌平区 102206)
0 引言
我国风电的开发建设已进入分散式与集中式并重的阶段。分散式风电以就地消纳为原则,相比集中式风电没有“弃风”问题和技术限制。就地消纳的分散式风电恰好与分层分区、就近平衡的无功补偿原则相契合。若对分散式风电的无功输出能力合理利用,可以改善系统电压、优化系统网损,减少无功补偿设备投资。分散式风电无功电压协调控制技术逐步成为目前的研究热点。
分散式风电无功电压协调控制技术主要针对控制模式、电压控制节点选择以及无功电压控制策略展开研究。传统分散式风电运行采用集中式控制模式,本文参照微网、主动配电网中新能源的三种控制模式:集中式、分散式、分布式控制模式[1-2]。集中式控制模式易于控制策略实现,但不能实现“即插即用”,扩展性差;中央控制器需要采集处理全局信息,随着发电单元数量增加计算负担过大;中央控制器与发电单元的远距离通信建设成本增加,可靠性降低[3-5]。分散式控制实现了发电单元的“即插即用”,扩展性好,鲁棒性强,发电单元间不需要进行信息交换,免去了通信建设的成本,但无法实现全局协调控制[6]。分布式控制存在控制中心与系统中某个或几个发电单元存在通信联系,各发电单元间利用局部通信网络交换信息,基于分布式控制算法实现各单元间的协调控制。分布式控制算法主要有任务分解法和一致性算法[7]。本文主要讨论基于一致性算法的协同控制,一致性算法就是解决系统中的一致性问题,系统各节点通过与邻近节点信息交互进行状态更新,使各单元状态量收敛为同一值。
无功电压控制策略的有效实现离不开电压控制节点(简称“控制节点”)的合理选择。文献[8–10]选风电机组并网点高压侧作为控制节点,由于分散式风电的接入使潮流方向发生变化,电压下降[11],该控制方式可能出现电网电压越限;文献[12-13]为防止因潮流改变引发的电压越限,选取网络中电压越限最严重节点作为控制节点,调压过程中易出现电压偏差发生改变,增加了电压调节次数。电压稳定性研究中电网薄弱节点的概念为控制节点的选择提供了新方向;文献[14-16]通过灵敏度大小、灵敏度指标判别式、灵敏度变化率来确定电网的薄弱区域;文[17]针对分布式电源接入电网造成的影响,提出灵敏度分析法确定系统电压的支撑点和薄弱点。目前控制节点选择均考虑单一因素,没充分考虑系统中节点电压与无功的内在联系,该选择方式存在一定盲目性,不能准确反映系统的调节需求,调压后仍存在节点电压越限或调压过程中增加电压调节次数。
无功电压控制策略与控制模式的选择密不可分。集中式控制模式下的各种控制策略易于实现[12-13,18-22],但发电单元的增加,通信网络也要增加系统建设成本,可靠性和可扩展性较差[23]。分散式控制模式下的控制策略只考虑本地信息[24-27],不能实现全网协调控制,无法完全避免电压越限。分布式控制模式具有经济性好、鲁棒性强等优点[3,28-29],但分布式控制模式下的控制策略尚未在分散式风电中应用无功电压控制策略技术。本文结合分布式控制模式与分散式风电特点,提出分布式控制模式的分散式风电协同控制策略。
1 控制节点选择
1.1 电压-无功灵敏度
节点数为n 的网络中,根据牛顿-拉夫逊法潮流计算,可得节点功率修正方程:

式中: ΔPi, ΔQi为注入节点i 功率的不平衡量;Ui, δi为节点i 电压的幅值和相角。
式(1)写成矩阵形式可表示为

令 Δ P=0,可得电压与无功功率的关系式

1.2 网损-电压灵敏度
节点数为n 的电力网络中,根据潮流方程,节点i 注入的有功功率展开可得
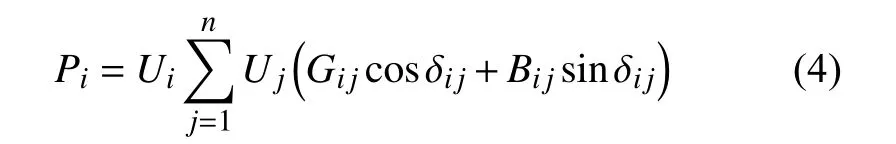
式中: Gij, Bij为 i,j 节点间的电导和电纳;δij为i,j 节点间电压的相角差。
根据系统各节点功率关系,网损方程可表示为
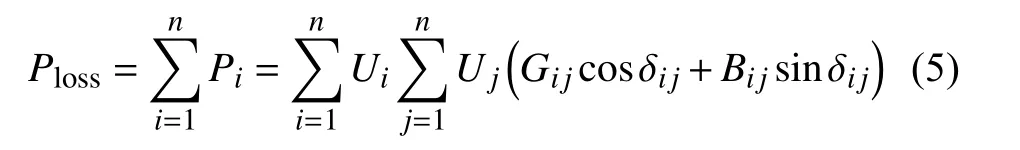
式中: Ploss为系统网损。
由此可以得到网损-电压灵敏度为[30]

1.3 电压偏差量
定义节点i 电压偏差量如式(7)所示,需要说明的是,本文所定义的电压偏差量并不等同于电能质量中的电压偏差。
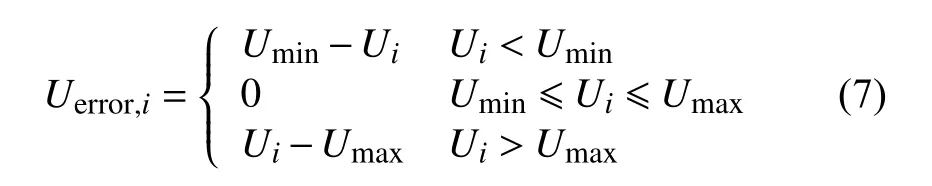
式中:35 kV 及以上供电电压时,Umax=1.05,Umin=0.95;20 kV 及以下供电电压时,Umax=1.07,Umin=0.93[5]。
1.4 综合选取控制节点
节点的电压偏差量、电压-无功灵敏度及网损-电压灵敏度量纲不同,不能直接进行运算,采用极差归一化法将其归一化。


2 无功指令计算
根据灵敏度分析理论,网络中任意节点电压变化量可以表示为[31]

将 λUerror,k作为电压变化量代入式(12),且认为网络负荷以及风机有功出力不变,得式(13)。 Uerror,k为 控制节点k 的电压偏差量, γ值取±1,在节点k 电压越上限时取负值,越下限时取正值; δU为电压调节的裕度,防止负荷或者风电机组出力的波动引发电压频繁上下穿越允许范围边界。 δU的取值根据实际情况进行选择,本文取 δ U=0.01。
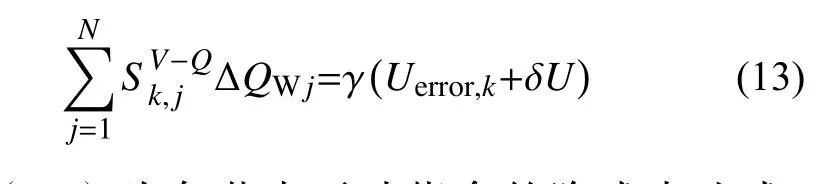
式(13)为各节点无功指令的隐式表达式,下文依据该式及无功指令分配方法计算各节点无功指令。实现对节点电压的精确调控,减少因灵敏度计算带来的误差,此处采用闭环控制,根据式(13)设计电压控制器。设计的无功指令生成环节如图1所示,图中 Tp、Tc为测量延时和传输延时;ΔQW为系统各节点总无功需求; ΔQWmax、 ΔQWmin为系统当前无功储备极限值。死区的设置是为防止控制节点电压频繁波动引发无功需求量的频繁变化。

图1 无功指令生成环节Fig.1 Generating link of reactive power instruction
3 无功指令分配
3.1 不同节点之间无功指令的分配
不同节点之间的分配方式主要有两种:公平法[32]和潮流灵敏度法。公平法令每节点风电机组无功出力占比相同,较常见且易实现,但调压具有盲目性,本文不做过多介绍;潮流灵敏度法把电压-无功灵敏度作为权重对无功变化量进行分配[12],如式(14)所示:

式中: C1为确定常数。
潮流灵敏度法针对一个节点进行调节,系统各节点电压之间的耦合关系使该种方法仍具有一定的盲目性,容易出现被调节点的电压恢复正常,其他节点电压越限的情况,需要进行多次电压调节,不利于系统稳定。本文在潮流灵敏度法基础上,考虑控制节点,和其他越限节点,提出一种基于多重电压-无功灵敏度的无功分配方法,使其不仅可以对控制节点电压实现有效调控,还针对其他越限节点电压进行调控,减少电压调节次数,提高系统运行的稳定性。利用其他越限节点的电压-无功灵敏度对现有潮流灵敏度法所得的无功指令进行再分配,式(14)变形为:

式中: SE为所有越限电压节点集合;C2为某一确定常数。
联立式(13)、(15)得此时第j 个节点风电机组的总无功变化量 Δ QWjref为:

由式(15)、(16)可得:

令各风电机组第k 次调压初始无功出力QWj0(k −1),则第j 个节点风电机组的总无功出力QWjref(k)如式(18)所示,多次电压调节时按该式迭代进行求取。

3.2 单一节点不同风电机组之间无功指令的分配
单一节点不同风电机组之间遵从公平的原则,各风电机组无功出力与其无功极限之比相等,即:
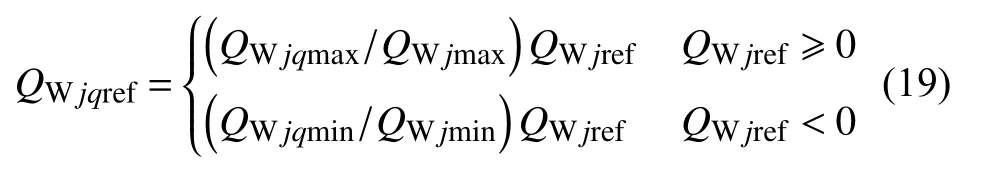
式中: QWjqref为接在第j 个节点的第q 个风电机组的无功指令; QWjqmax、 QWjqmin为接在第j 个节点的第q 个风电机组的无功出力上、下限;QWjmax、 QWjmin为接在第j 个节点的所有风电机组的无功出力上、下限之和。
3.3 风电机组内部无功指令的分配
全功率变换机组无需进行内部无功指令分配,但对于双馈风电机组,无功指令分为网侧变流器无功指令和定子侧无功指令,两部分相互独立。使变流器处理的无功尽量少,考虑网侧滤波电路易产生损耗,风电机组内部无功指令优先分配给定子侧,当达到定子无功极限时再把剩余无功指令给网侧变流器。
综上,改进的分层无功控制策略如图2 所示。
4 分布式控制模式下分散式风电协同控制策略
4.1 图论基础
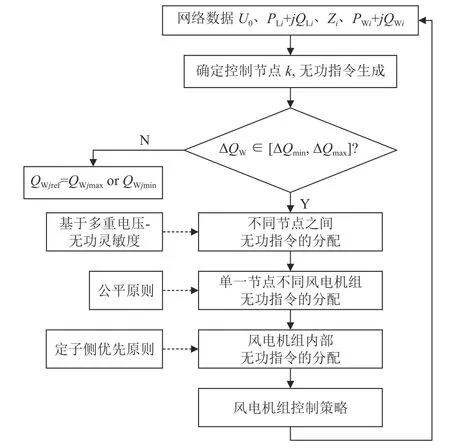
图2 改进的分层无功控制策略流程图Fig.2 Flowchart of improved hierarchical reactive power control strategy flowchart
对于一个分布式控制系统,其网络结构可以由一个有向图来表示,记作 D=(V,E),其中V={1,2,···p} 是 节 点 集, E={(i,j)|i ∈V ∧j ∈V}是V的支路集,也即有向图弧的集合。对应分布式控制模式中,节点即为各发电单元,各单元间的通信网络即为图中的支路,支路 e=(i,j)表示发电单元 j可以接收发电单元i 的信息。若节点i , j之间存在点弧交错序列 { i,(i,k1),k1···(kl,j),j},则该序列即为i , j 之间的路,称i 对 j 可达。若 ∃i ∈V,图内任意节点均可达,称i为全局可达节点,即领导节点[7],此时 D为连通网络。若 ∀i,j ∈V , i 、 j相互可达,则称 D是强连通网络。本文认为两节点存在的通信联系均可实现双向通信,对应图 D为无向图,当存在全局可达节点时, D 为强连通网络。

根据节点之间的邻接关系构建通信矩阵[3,33]即邻接矩阵:
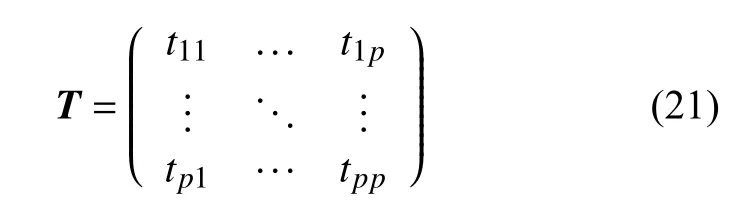
通信矩阵元素下标为两节点标号, tij=1时表示节点i与 节点 j 存在直接通信联系, tij=tji=1时代表节点i 、 j 可实现直接双向通信; tij=0代表节点i 、 j无直接通信联系。显然,该矩阵对角线元素均为1,当T 矩阵为单位矩阵时,对应于分散式控制模式。若将通信矩阵列写为时变矩阵,则可以体现电力系统中检修、停机等行为[2,34]。
4.2 基于一致性算法的分散式风电协同控制策略
一致性算法[4]可以分为有领导一致性算法和无领导一致性算法。有领导一致性算法中,无差别选择某一全局可达节点作为领导者,功能类似中央控制器,领导节点通过接收调度指令收集各节点信息,控制目标计算状态量,响应系统变化,其余跟随节点状态量随之变化,最终所有节点状态量通过迭代更新达到一致,实现控制目标。无领导一致性算法中所有节点相互独立,整个系统是一个完全去中心化的状态,没有收集全局信息的节点,各节点通过局部通信网络相互迭代更新达到全局目标一致。与领导一致性算法相比无领导一致性算法更简单,易实现,本文选取有领导一致性算法进行研究。
选取节点1 为领导节点,领导节点1 可以接收全网信息及调度指令。假设领导节点的状态量为 α1, 系统受控量为χ,当所有量均在合理范围内,控制目标可以表示成[35]:

式中: χref为系统受控量参考值,即为控制目标值;αi(i=2,3,···p)为跟随节点的状态量。
根据有领导一致性算法,领导节点的状态量α1的迭代式如式(23),式(23)构成了一个反馈系统,通过将受控量参考值和当前值之差反馈给状态量,并对状态量进行不断修正,使得状态量趋于一个稳定的值。式(23)保证了状态量在修正过程中不会越限,始终在合理范围内。

式中: ε为收敛系数, ε >0。
跟随节点的状态量在相互通信联系节点的状态量进行加权更新。由于任一节点与其他节点通信距离及节点间的通信网络的可靠性不尽相同,每条通信路径传输的状态量信息的精确性也不相同,采用加权矩阵W 表征某一节点所接收其他节点传输状态量信息的可信度,可信度越高权重越大。加权矩阵的元素根据多种因素确定,如通信距离、通信网络可靠性等,跟随节点状态量可以表示为:

基于此,提出适应分布式控制模式的分散式风电协同控制策略。相比集中式控制,基于分布式控制模式的控制策略的不同主要在于无功指令生成方式。集中式控制,中央控制器将相异的无功指令经通信线路传输给各风电机组,以实现电压调节,该种控制模式发无功指令可以辨别控制对象,不同风电机组接收不同的无功指令。分布式控制,主要利用分散式风电机组间局部通信网络来实现系统整体目标,指令传达具有无差别性。即网络各机组间通信线路上传输的指令值是相同的,该指令值即前文所提“状态量”。根据一致性算法,首先确定系统受控量以及系统状态量,然后设计状态量生成环节及各机组无功指令生成环节,新设风电机组时仅需新设的机组与系统中任一现有机组建立双向通信联系便可进行控制的目标。
根据一致性算法,系统受控量 χ为控制节点k的电压 Uk, 系统受控量参考值 χref为:

系统中各风电机组统一状态量 α可以从式(16)提取得到,如式(26)所示。该式对系统任意风机接入点具有无差别性,任意风电机组均要接收并达到该状态量。

为方便表示,风机接入节点即为 SW包含的所有节点,则存在等式:

综上所述,任取领导节点j,设计领导节点状态量生成环节如图3 所示。死区的设置是为了防止控制节点电压频繁波动引发领导节点状态量频繁的变化。

图3 领导节点状态量生成环节Fig.3 State quantity generating link of lead node
各风电机组在接收到状态量之后不能直接利用,需经状态量-无功指令转换环节生成无功指令再提供给风电机组内部控制策略的端口。根据式(22)以及定子侧优先原则(仅双馈风机),假设每个节点的风电机组型号及容量相同,当系统状态量大于0 时,可设计节点i 的风电机组无功指令如图4 所示,图中 QWismax为节点i 处接有风电机组的最大定子无功输出。当状态量小于0时与之类似,不再赘述。

图4 风电机组无功指令生成环节Fig.4 Reactive power instruction generating link for wind power generation unit
5 算例
为验证所述无功电压控制策略,搭建某实地配电网模型验证,拓扑如图5 所示。此模型共9个节点,节点1 接上级220 kV 电网为平衡节点,其余节点均为PQ 节点。节点4、节点6、节点8分别接有5、3、2 台风电机组,每台风电机组型号相同,参数如附表A1 所示。初始运行状态时,各风电机组运行于单位功率因数模式,无功指令均为0,节点4、节点6、节点8 所接风电机组的初始风速分别为9 m/s、8 m/s、7 m/s。仿真算例中的变压器参数、线路参数、负荷参数分别如附表A2、附表A3、附表A4 所示。选取目前的主流机型-双馈风力发电机作为研究对象。
本工况负荷为原先的75%。节点4、节点6、节点8 所接风电机组的风速1.5 s 时分别由9 m/s、8 m/s、7 m/s 变为10 m/s、10 m/s、8 m/s。此时出现节点电压越上限,初始节点电压、出现此工况后各节点电压、出现此工况时节点电压偏差量以及归一化的结果如表1 所示。

图5 仿真算例拓扑图Fig.5 Topological graph for simulation example
确定控制节点为节点4,对比潮流灵敏度无功分配方法及本文提出基于多重电压-无功灵敏度的无功分配方法,节点电压变化情况如图6 所示。
由图5 仿真结果可得,系统部分节点(节点4、6)电压越上限的情况下,应用潮流灵敏度法以及多重电压-无功灵敏度法分别对无功指令进行分配,经过一段动态过程后各节点电压均降至允许范围内。潮流灵敏度法,仅实现了对控制节点4 的有效调控,另一越限节点6 的电压经调节后仍靠近电压限制边界。在风电出力以及负荷的不确定性中,某个因素或多个因素的影响下,节点6 电压易再次越过限制。应用本文所提多重电压-无功灵敏度法,不仅实现了对控制节点的调节,还有效调节了其他节点的越限电压,减少了调节电压的次数,提高了系统的稳定性。
在上述仿真算例的基础上,假定节点4 的风电机组为分布式控制中的领导节点,可获取全网信息及调度指令,将节点4、6、8 处的所有风电机组分别处理为分布式控制中的单个节点,带有通信线路的仿真算例拓扑图如图7 所示。图中的4、6、8 节点作为分布式控制中的3 个节点,可得到此时的通信矩阵:
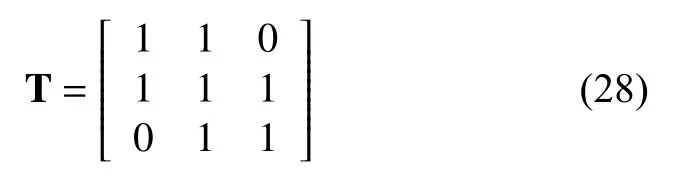
跟随节点状态量迭代表达式为:

由此分别依前文工况进行仿真验证。

表1 各节点电压及归一化结果Table 1 The voltage of each node and the result of normalization
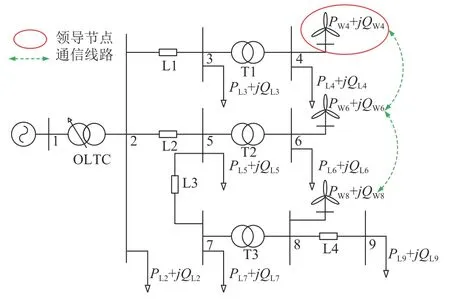
图7 带有通信线路的仿真算例拓扑图Fig.7 Topological graph for simulation example with communication link
负荷为原先的75%。节点4、节点6、节点8所接风电机组的风速在1.5 s 时分别由9 m/s、8 m/s、7 m/s 变为10 m/s、10 m/s、8 m/s。为使电压变化明显,容易观察,令风电机组2.5 s 时参与电压调节。此时各节点电压变化情况如图8 所示,为便于读图,此处仅给出电压最高的4、6、8 节点,状态量 α变化情况如图9 所示,4、6、8 节点单台风机无功变化情况如图10 所示。

图8 各节点电压随时间变化情况Fig.8 Nodal voltages varying with time
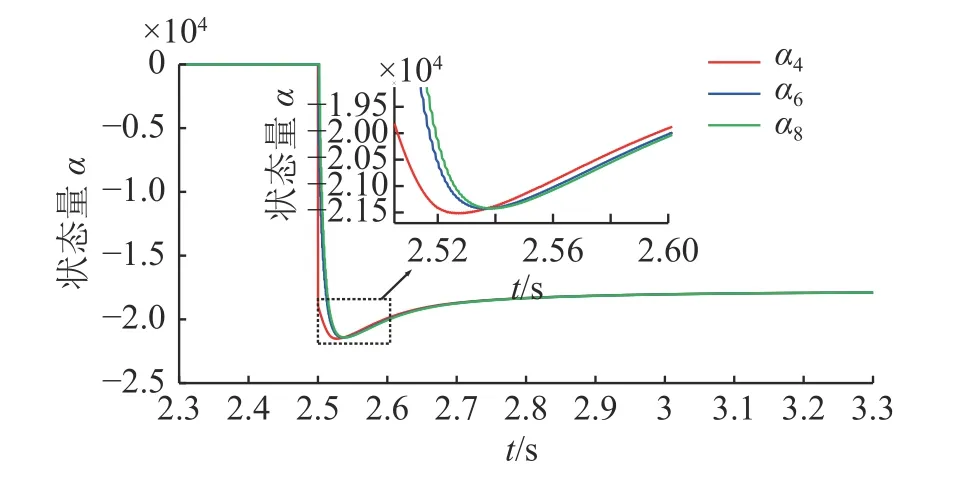
图9 状态量 α随时间变化情况Fig.9 State quantity α varying with time

图10 各节点单台风机无功指令随时间变化情况Fig.10 Reactive power instruction of single wind turbine at each node varying with time
由图8~图10 可以看出,分布式协同控制下,风电机组在2.5 s 时参与电压调节,状态量 α经一段时间的动态后收敛到一个定值,系统趋于稳定,各节点无功按照多重电压-无功灵敏度法分配,系统越限电压均按照控制目标回归正常,分布式控制模式实现了给定的控制目标。
6 结论
1)本文提出的控制策略通过考虑系统中所有电压越限节点,充分发挥风电机组的无功输出能力,调压过程中减少了系统调压次数,提高了配电网电压调节的经济性和灵活性。
2)基于分布式控制理论和一致性算法的分散式风电协同控制策略,利用局部通信网络使各发电单元状态量逐渐趋近于同一值,实现系统控制目标。该控制策略不需要传统集中式控制下的通信线路等设备的巨额投资,提高了系统运行的经济性。
系统中新建发电单元只需就近与现有发电单元建立双向通信联系以保证通信完备,便可实现控制目标,提高了系统的可扩展性。若发电单元间通信路径不止一条,出现故障后控制策略仍可起作用,提高了系统的鲁棒性。
3)通过仿真验证了控制策略的正确性。
附录A

附表 A1 算例参数Table A1 Parameters of equipments used in calculation example

附表 A2 变压器参数Table A2 Transformer parameters
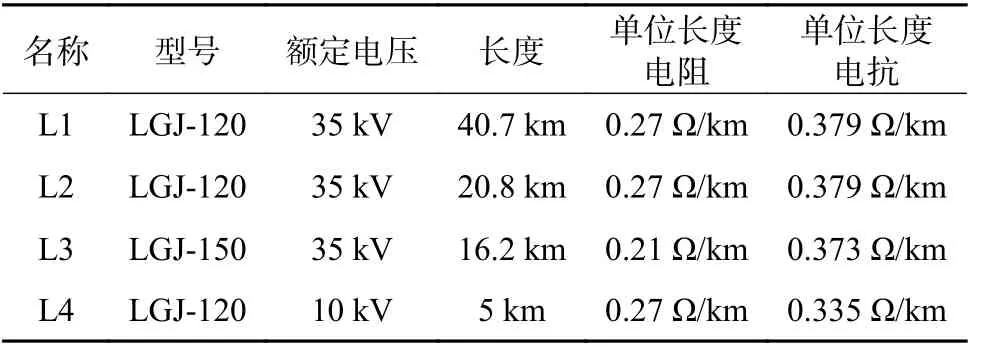
附表 A3 线路参数Table A3 Line parameters

附表 A4 负荷参数Table A4 Load parameters
(本刊附录请见网络版,印刷版略)
