基于最优最劣法-熵权-逼近理想解排序法的电网安全与效益综合评价
2021-02-22艾欣秦珺晗胡寰宇王智冬彭冬赵朗
艾欣,秦珺晗,胡寰宇,王智冬,彭冬,赵朗
(1. 华北电力大学电气与电子工程学院,北京市 昌平区 102206;2. 国网经济技术研究院有限公司,北京市 昌平区 102209)
0 引言
近年来,我国正逐步推进能源清洁低碳转型,大规模发展可再生能源,众多交互能源设施(如:分布式能源、储能、电动汽车等)快速发展。随着“电力物联网”的整合与发展的提出,推动了由电网向能源互联网的升级和跨越,改变了传统电网的赋能形式,通过数字化的管理模式以及运用“云大物移智链”等先进信息技术,使得电网的感知能力、互动水平和运行效率得到提升,并获取整合越来越多种形式的能源,使能源利用率逐步提升,由“用好电”向“用好能”转变[1]。衡量转变的一个有效途径就是对电网发展进行科学合理的评价,而在电网决策与评价方面的重要问题之一就是平衡经济优化、节能环保与系统安全运行之间的矛盾,具体体现在:第一电网企业的属性决定了它追求电网效益的特性;第二电网必须连续稳定运行的要求决定了电网安全尤为重要[2]。因此,电网安全与效益综合评价体系的构建,利用数学模型对评价对象做出整体性的评估,结合评价结果进行排序、择优,使电网的规划更好地满足电力发展需求日益重要。
国内外已针对电网电能质量[3-5]、电网安全性[6]等各方面提出了多种综合评价方法。国外学者对于电网发展的综合评价研究大多集中于电网的供电质量[7]、可持续发展[8]、智能化发展[9]等方面。目前,国外对电网的综合评价体系研究有:文献[10]依据效果和主要特性两类指标构建的美国智能电网评价体系;文献[11]由美国电科院依据电网建设及项目收益所构建的综合评价体系;文献[12]结合市场、安全与电能质量和环境3 个方面建立了欧洲电网效益综合评价体系等。在我国,电网发展的评价也逐渐受到众多学者和专家的重视,主要集中于利用数学模型对电网发展进行综合评价。文献[13]提出德尔菲−熵权综合权重法对电网规划方案进行综合决策;文献[14]提出基于区间层次分析法(analytic hierarchy process,AHP)对城市电网规划进行综合评判;文献[15]依据逼近理想解排序法(technique for order preference by similarity to an ideal solution,TOPSIS)对考虑安全事故的运行规划进行优化;文献[16]利用改进G1-TOPSIS 法对智能电网进行了层次化评价;文献[17]提出利用层次分析法与反熵权法相结合的权重计算方法来评价电网运行状态;文献[18]提出基于层次分析法和熵权法结合的方式对电网调度进行评价。上述学者多是通过算法得出主客观权重之后进行简单的加权求平均计算得到综合权重,进而对电网进行评估,主客观权重之间影响较大。文献[19]利用多算子模糊层次分析法确定权重并对电网安全与效益进行综合评价,但仅考虑指标间的主观权重,主观意识过强。
本文在文献[19]搭建指标体系方法的基础上,提出一种最优最劣法(best worst method, BWM)-熵权-TOPSIS 法综合评价方法。首先,搭建计及电网规划基本属性和用电客户自身需求的电网安全和效益综合评价指标体系;其次,采用BWM 和熵权法确定主客观权重,将博弈论结合到综合权重的计算中,以NASH 均衡作为协调优化目标,并通过TOPSIS 法计算被选方案和理想方案之间的距离从而进行综合评估;最后,利用该方法对国网经研院在2017 年对全国25 个省份返回数据中的安全与效益方面共16 个指标进行实例分析,对各省份电网进行安全与效益方面综合评价,验证了该方法的可行性,并利用指标灵敏度分析方法展现部分评价指标变化对总体评价结果的影响,提出相关改进措施。
1 电网安全与效益综合评价指标体系
1.1 指标选取原则
电网综合评价中所涉及的指标数量十分庞大、表现形式多样,快速、有效地筛选关键指标,对后续进行合理评价工作十分重要。本文在筛选指标时所遵从的原则[20-21]如下文所述。
1)一致性原则:被选取指标要和评价目标一致,选择具有代表性的关键指标,通过计算来反映电网发展现状和未来发展能力。
2)层次性原则:电网综合评价体系是一个复杂的系统,在构建指标体系时应具有一定层次性,看起来更加清晰。
3)独立性原则:体系中不同的指标之间应具有较强的关系并且同一层级间指标不相互重复。
4)可比性原则:所选取指标能够直观的将电网发展过程中某方面的特性展现出来,并且能够相互比较。
1.2 指标体系构建
电网发展安全与效益是反映电网发展状况的基本依据。针对电网效益的提升,一方面体现在安全性角度,比如:通过减少停电次数使售电量得到提升;另一方面,我国目前大力发展可再生能源,电网不仅要对传统能源进行输送以达到自身经济效益,同时要接纳风电、光伏等可再生能源。由于分布式能源具有波动性、不可控性等特点,导致其对电网运行造成一定影响,因此,电网在减少碳排放、可再生能源接入等方面的效益也应考虑到电网综合评价指标中。
本文根据全国25 个省份的实际情况,从电网安全和效益2 个方面构建指标体系[22]。为使评价更加清晰、容易实现,将指标分为4 层,分别为目标层、类别层、一级指标层以及二级指标层。即最终评价目标是电网安全与效益,将具体表现全年电网变化的16 个指标分为电网安全与电网效益两类,又分别从3 个方面选取指标得到最终综合评价指标体系,详见表1。

表1 电网综合评价指标Table 1 Comprehensive evaluation indices of power grid
2 BWM-熵权-TOPSIS 综合评价模型
BWM-熵权-TOPSIS 综合评价方法是先通过BWM 法和熵权法分别计算各项指标的主客观权重,使权重不仅包含数据本身的信息,还可体现专家们的主观判断。再以NASH 均衡作为协调目标将博弈论引入综合评价,得到一个较均衡的综合权重;最后,与TOPSIS 法相结合,对被选方案进行排序。
2.1 BWM 法计算主观权重
BWM 法是荷兰学者Rezaei 于2014 年提出的一种确定指标主观权重的新方法[23]。
在以往的多指标决策问题中,最常用的方法是AHP 法,AHP 是将任意2 个指标相互比较以得到指标的评价矩阵,需要进行 n(n−1)/2次比较,最终得到 n2−n个数据,过程复杂,比较次数多,会使专家存在一定的失误,导致错误率高;而BWM 则通过选择出最优和最劣2 种指标,并分别与其余指标进行比较,只需要2n-3 次,简化了AHP 的繁琐过程,数据量也大大减少,降低了由于数据过多使专家思维混乱而导致的失误,更容易通过一致性检验,提高了可靠性。
具体步骤如下文所述。
1)在指标集 X={x1,x2,···,xn}中根据专家意见选取最优指标 XB和 最差指标 XW。
2)专家采用1—9 分制来进行评分,确定其他指标相对于最优指标的重要性。构造比较向量CB=(CB1,CB2,···,CBj), 其 中, CBj代 表 最 优 指 标与指标 j 相比的重要性,1 代表 CB和 CBj同等重要,9 代表 CB相 比 CBj极端重要。
3)确定其他指标相对于最劣指标的不重要性,构建比较向量CW=(C1W,C2W,···,CjW)T,其中,CjW代 表最劣指标与指标 j相比的最不重要性,1代表 CjW和 CW同 等不重要,9 代表 CjW相 比 CW极端不重要。
4)由目标规划模型,建立数学规划式并求解,得出最优指标权重

式中: ωB为 CB的 权重; Cj为 准则向量; ωj为 Cj的权重,即指标实际权重; ωW为 CW的 权重; aBj代表 CB对 Cj的 重要程度值; ajW代 表 Cj对 CW的重要程度值。可转化为

5)计算一致性比率。
将所得 k 用 k∗表 示,由求得一致性比率CR(CI为给定值),越接近0 代表一致性越好,为0 时即为完全一致。
若有 p位专家参与判断,则将对评分结果进行加权平均计算,得到最终权重:
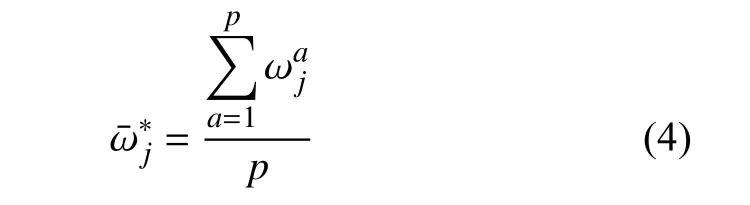
2.2 熵权法计算客观权重
熵权法[24]是一种客观的赋权法,根据指标包含的信息量多少来确定每个指标的权重。在多指标决策问题中,一个指标的信息量越大,其变化程度也就越大,熵值则越小,进而在方案综合评价中的作用就越大,该指标权重也越大,避免主观因素的影响,使计算出的权重更加可靠。
2.2.1 指标的标准化处理
在指标集中,各指标的单位、量级等方面存在较大差异,因此,在计算权重前需要对所有指标进行无量纲标准化处理,保证它们的取值范围在[0,1]之间。本文通过Min-max 标准化处理方法[25]对评价指标 xij进行标准化处理。
假设有 m个分析对象, n个需求指标,初始决策矩阵为 X=(xij)m×n:

式中 xij为第i个 省的第 j个指标。
对于越大越好的指标值:

对于越小越好的指标值:

式中: min(xi) 和 max(xi)分别为指标i 的最小值和最大值; bij为指标 xij经过标准化处理后的结果。
标准化后,评价指标 0 ≤bij≤1,即把指标矩阵E 规范化,得到矩阵

2.2.2 熵权法计算权重
熵权法确定权重的步骤如下文所述。
1)计算第j 项指标下第i 个方案所占的比重:
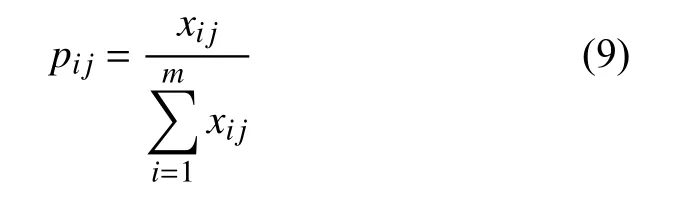
2)第 j个评价指标的熵值:
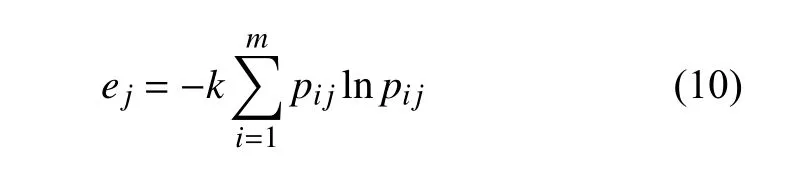
3)计算指标 j 的熵权 ωj:

2.3 基于博弈论的BWM-熵权综合权重法
在上述计算中,无论是运用BWM 法得出主观权重还是利用熵权法求得客观权重,都未能全面地考虑指标所有信息。因此,众多学者通过加权求平均的方式计算综合考虑主客观权重的组合权重,但在计算时主客观权重之间的相互影响较大,合理性较差。通过引入博弈论,将NASH 均衡作为协调主客观权重的一个优化目标,在不同权重之间找寻一个平衡点,使得最后所求综合权重与各个基本权重之间偏差尽可能地达到最小,进而得到一个较为合理的综合权重[26]。具体步骤如下文所述。
使用 v种方法对综合评价指标体系中的各指标进行权重确定,由此构造一个基本权重集h={h1,h2,···,hv}, 将其中的 v个向量任意线性组合构造一个综合权重集:
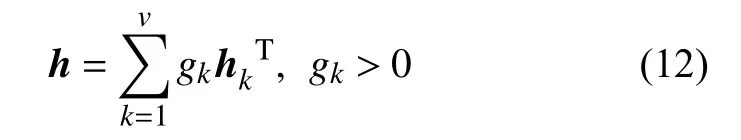
上述公式中 v 个线性组合系数 gk需要利用博弈论模型进行优化,目的是使 h与 各个 hk的偏差极小化,进而从综合权重集中找寻到最合理的权重h∗,因此,导出博弈模型为

其本质是通过将多个综合权重向量进行交叉组合的规划模型,依据矩阵微分性质,得到最优化一阶导数条件为

计算可求得 (g1,g2,···,gv),接着对其进行归一化处理:

因此,得到综合权重为
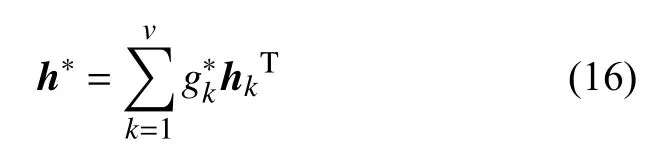
综合权重集为 H=[h1,h2,···,hv]T。
2.4 BWM-熵权-TOPSIS 综合评价模型
TOPSIS 法是在现有的对象中进行相对优劣的评估,可用于通过较多个指标来对多个备选方案进行评价选择的情况[27]。此方法的基本原理是依据计算出的各个被选方案与最优解和最劣解之间的距离进行排序、择优。如果评价对象与最优解最接近,同时又与最劣解距离最远,那么此被选方案为最好方案;相反,就是最差方案。具体计算步骤如下文所述。
1)原始数据标准化,同上述熵权法一样,见公式(5)—(7)。
2)计算加权规范化决策矩阵 Z。
对于指标集 X={x1,x2,···,xn}的最优组合权重矩阵为 A=[ω1,ω2,···,ωn]T,将进行标准化处理后的规范化矩阵 B=[bij]m×n点 乘组合权重矩阵 H即可算出指标加权规范化矩阵 Z。

3)计算被评价对象的最优理想解和最差理想解:

当 j 为效益型指标时越大越好,当 j为成本型指标时越小越好。
4)计算每个方案到最优理想解和最差理想解的欧氏距离:


5)确定样本点到最优理想解点和最差理想解点的相对贴合度:
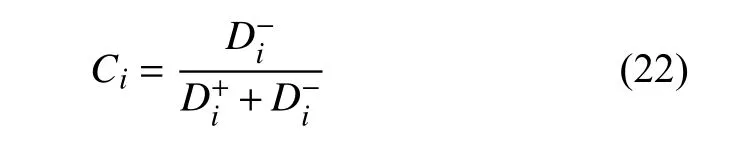
6)将上一步的计算结果按大小排序,即各个方案的优劣顺序。计算流程如图1 所示。

图1 计算流程图Fig.1 Flow chart of calculation
3 案例分析
本文针对2017 年国网经研院对25 个省份电网发展诊断反馈数据作为原始数据,从电网安全和效益两方面选取16 个指标通过上述方法和评价体系进行评估。
3.1 权重的计算
1)对于主观权重的计算由3 位专家逐一打分,分别通过BWM 法和AHP 法计算各指标主观权重值并进行一致性检验得证,判断矩阵有效,同时将2 种方法所得的一致性比率进行对比,见表2,虽然二者比率值差别不大,但是BWM 法计算出的结果更接近于0.1,可靠性更高。通过加权求平均计算每层指标权重值得到16 个二级指标主观权值:

2)通过熵权法,由公式(5)—(11)可得出16 个指标客观权重值:=[0.045,0.051,0.041,0.04,0.043,0.038,0.056,0.066,0.058,0.06,0.073,0.108,0.111,0.054,0.1,0.056]。
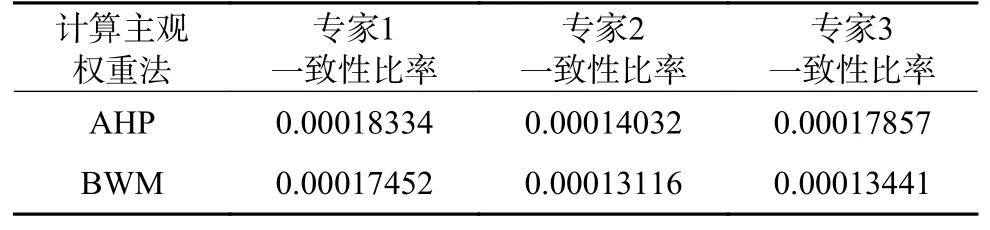
表2 一致性比率对比表Table 2 Comparison of consistency ratio comparison
3)考虑博弈论模型通过公式(12)—(15)求得主、客观权重的NASH 均衡解:根据组合权重公式计算各项指标组合权重值:ωj=[0.057,0.056,0.047,0.044,0.043,0.052,0.084,0.058,0.053,0.063,0.062,0.107,0.1,0.052,0.07,0.052]。
同时,利用目前常用的通过Lagrange 乘子法求解算最优组合权重方法也进行了综合权重的计算,方法如下文所述。
设定最优组合权重为 ωj(j=1,2,···,m),若使最优组合权重 ωj与尽可能接近,依据最小鉴别信息原理,建立如下目标函数:

通过Lagrange 乘子法求解,得到最优组合权重:
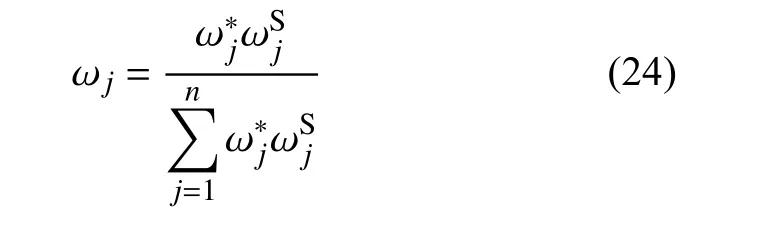
鉴于计算数据过多,从中选取6 个指标,分别通过2 种方法进行综合权重计算并对计算结果进行了对比(见表3)。

表3 综合权重对比表Table 3 Comparison of comprehensive weights
通过对比可以看出,2 种方法计算结果虽较为相近,但通过NASH 均衡求解得到的综合权重受主客观权重的影响较小,所得结果更为合理。
3.2 基于TOPSIS 法计算得分评价值
将加权规范化后的指标矩阵Z 代入公式(17)—(22)中,即可算出各个被评价对象的相对贴合度:
C=[0.042,0.023,0.046,0.053,0.041,0.055,0.038,0.028,0.047,0.024,0.01,0.049,0.032,0.037,0.026,0.07,0.012,0.05,0.034,0.056,0.043,0.046,0.035,0.061,0.053]。
本文方法针对25 个省份共计16 个指标进行安全与效益评价最终得分与排序(见表4)。
通过计算并结合原始数据、所得综合权重和最终得分排序可以看出,无论从电网安全方面还是效益方面,省份A 各方面都严格把控,从未出过事故隐患,单位电网资产售电量等也都处于前列,因此,得分最高。而排分靠后的地区,多是由于新能源发电设备大量接入,无法保证电能质量,也不能满足用电需求,导致评分较低。但大部分城市综合权重和得分相差不多,无较大差别,可以看出大多数城市电网发展安全与效益程度稳定。
4 灵敏度分析
依据2017 年各个指标原始数据,以A 省份为例,使指标数值在−50%至+50%的范围内变化,通过单指标灵敏度分析和多指标组合灵敏度分析观察综合评估值与主要指标的关系变化。
4.1 单指标灵敏度分析
在安全和效益16 个指标中各选取3 个指标做单指标灵敏度分析,得到图2 所示的灵敏度分析变化曲线。通过各指标曲线斜率的变化大小可以反映出该指标对综合评估的影响,斜率变化越大代表该指标对综合评估值的影响就越大,反之亦然。

表4 各省综合得分及排序Table 4 Synthesis scores of all provinces and sorting
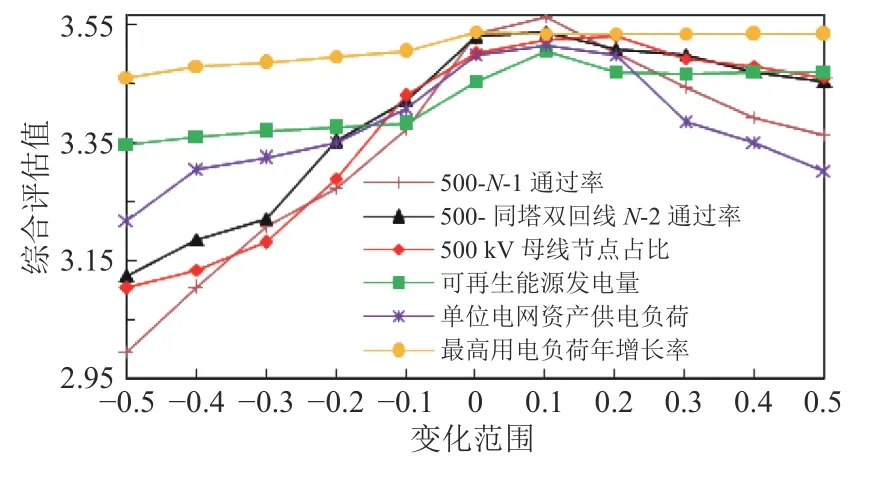
图2 单指标组合灵敏度分析变化曲线Fig.2 Varying curve of single index combined sensitivity analysis
观察分析图2 可以看出,500-N-1 通过率曲线的斜率绝对值最大,将其从2017 年原始数据基础上逐渐减小至−50%,综合评估值由3.53 下降至2.994;逐渐增大至+50%,综合评估值从3.53下降至3.36。因此,当该指标值保持在实际值不变或增加+10%时,对应综合评估值最大。在实际中,判断电力系统安全性最重要的原则即为N-1 准则,当系统中任一元件发生故障而被切除后,应不造成因其他线路过负荷跳闸而导致用户停电,不破坏系统的安全稳定性,因此,网络安全中N-1 检验尤为重要。
4.2 多指标组合灵敏度分析
文章主要研究电网安全与效益综合评价,故进行单个指标灵敏度分析后,综合考虑两方面指标同时变化对综合评估的影响,通过多指标组合灵敏度分析进行深入研究[28]。在电网安全与效益两方面中选取具有联动关系的指标进行组合,如表5 所示,给出了6 组指标组合。

表5 多指标组合Table 5 Combination of multi-indices
多指标组合灵敏度分析曲线如图3 所示,从图3 中曲线变化趋势可以看出,组合5 对综合评价结果影响最大,保持不变或增加10%新能源接入;紧接着为组合1 和组合2,其变化也较为明显,适当提升10%N-1 和N-2 通过率,可以使得电网安全提升。组合4 影响较小,曲线趋于平缓;而组合6 呈现波动向前变化,增加10%或减少10%都可以提高综合效益。
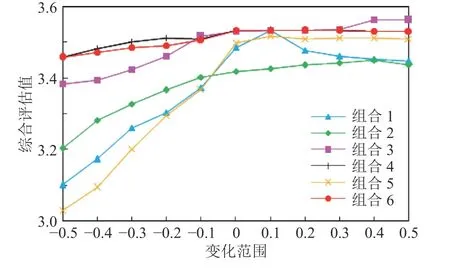
图3 多指标组合灵敏度分析变化曲线Fig.3 Varying curve of combined sensitivity analysis of multi-indices
5 结论
1)BWM-熵权法改善传统AHP 方法在计算主观权重时繁琐的过程,降低了不一致风险;同时结合了客观权重,将原始数据内部信息融合其中,通过NASH 均衡求解方式得到更可靠的综合权重,改善了以往所用的加权求平均算组合权重存在的主客观权重之间影响较大的问题,使最终得到的评价结果更加科学准确。
2)将所求综合权重引入TOPSIS,采用逼近理想解计算各个评价指标与参考点的距离,利用所得距离求解指标样本与理想样本的相对贴合度,通过对贴合度的排序实现电网安全与效益的综合评价。
3)通过对2017 年全国25 个省份电网安全与效益方面计算及指标间灵敏度分析验证该综合评价方法的可行性,对比分析电网之间优劣,结果表明,此方法既能有效的进行电网安全与效益方面的综合评价,又能客观反映方案中各个指标与理想方案的整体贴近程度,是一种有效的综合评价方法。
