胶合竹-混凝土组合梁抗弯性能试验研究

单波 邓钧远 叶芯 肖岩

摘   要：基于已有的推出试验，选择螺杆、凹槽和预紧力凹槽3种连接件，开展了5根胶合竹-混凝土组合梁的四点抗弯试验，研究连接件类型与数量对组合梁抗弯性能的影响. 试验结果表明，组合梁具有较高的初始组合效应，在正常使用极限状态内的组合效应相对稳定，且组合梁的抗弯刚度和承载力随连接件数量增加而提高;对于采用螺杆连接件的组合梁，其极限承载力取决于指接部位的抗拉强度;对于凹槽类连接件的组合梁，其极限承载力主要由端部连接件的抗剪切强度控制;采用预紧力凹槽连接件的半装配式组合梁与现浇施工方式的凹槽组合梁相比较，其抗弯性能很接近，但施工效率显著提高;欧洲规范EC 5中的等效截面刚度法高估了试件的承载力，不适合直接套用于组合梁.

关键词：组合梁;胶合竹;抗弯性能;组合效应

中图分类号：TU398.4                  文献标志码：A

文章编号：1674—2974（2021）01—0154—09

Abstract：Based on the existing pull-out tests on shear connectors， total five glued laminated bamboo （glubam）-concrete composite beams were tested under four-point bending loading to investigate the effect of connector type and numbers on the bending performance of composite beams. Three types of connector were selected in the current study including the screw connector，the notch connector and the pre-tightening notched connector. Test results show that all composite beams with different connectors exhibit high initial composite action and relatively stable composite action under the serviceability limit state. For the composite beams with screw connectors， the ultimate load carrying capacity is determined by the tensile strength of the glubam at the fingure joint. However， the ultimate load carrying capacity of the composite beams with notch connectors and the pre-tightening notched connectors mainly relied on the shear strength of the end connector. The semi-prefabricated composite beam with pre-tightening notched connectors shows the similar bending capacity when compared with the corresponding casting in-situ composite specimen， indicating a good prospect considering its high construction efficiency. The equivalent stiffness method predicted by Eurocode 5 overestimates the load carrying capacity of all specimens， and it is not suitable for glubam-concrete composite beams.

Key words：composite beams;bamboo;bending performance;composite action

我國木材资源匮乏，国内所需的木材严重依赖进口的方木和原木，这严重制约了我国现代木结构的发展. 但我国竹林资源丰富，尤其是具有丰富的大径级毛竹. 对毛竹进行破片重组胶合，制成高强度的工程竹材，并用于建筑结构，成为绿色建筑领域的研究热点[1-2].

胶合竹（glued laminated bamboo）是由单向竹帘正交层叠、热压胶合而成的一种工程竹材，最早由肖岩等[3-4]提出并开展研究. 为了与国外广泛应用的胶合木（glulam）相对应，肖岩等将胶合竹命名为glubam，目前已在竹木结构研究领域得到广泛认可. 肖岩等[4-5]已对胶合竹的材料、构件和结构体系进行了充分的研究，并建设了一批竹结构示范工程. 胶合竹的基本力学性能优于常用的结构木材，但相比于混凝土，其弹性模量低，使得胶合竹抗弯构件的刚度低，其承载力往往由变形控制，很大程度上制约了竹结构的跨度[6-7].

在现代木结构中，木-混凝土组合梁（Timber-concrete Composite Beams，TCC梁）是一种提高木梁刚度的有效结构形式. 在这一体系中，通过剪力连接件将上部混凝土楼板和下部胶合竹梁组合在一起， 两者形成组合效应，大大提高了抗弯构件的刚度[8]. 基于此，研发胶合竹-混凝土组合梁（Bamboo-concrete Composite Beams，BCC梁），是提高胶合竹抗弯构件力学性能、增大竹结构跨度的有效方式，具有一定的理论意义与工程价值.

国外的TCC梁/板研究成果十分丰富[9-13]，并在建筑工程中得到广泛应用[14]. 近年来，随着北美现代木结构的引入，一些国内学者开始关注TCC的相关研究，在新型连接件的设计及抗剪切性能，以及TCC抗弯性能及计算方法等方面进行了相关的试验和分析[15-18].

而在BCC的研究方面，目前还处于起步阶段. 单波等[19-21]研究了BCC销连接件和凹槽连接件的抗剪切性能，并提出了新型装配式、半装配式连接件;魏洋等[22]对3个销连接的BCC梁开展了抗弯试验. 相关研究都亟待系统化和深入化

本文基于BCC连接件抗剪切性能的研究成果[21]，选择多种典型连接件，开展BCC梁的抗弯试验，并评估欧洲规范EC5中TCC设计方法对BCC的适用性[23]，为BCC的设计与应用提供基础性依据.

1   组合梁设计及制作

1.1   组合梁设计

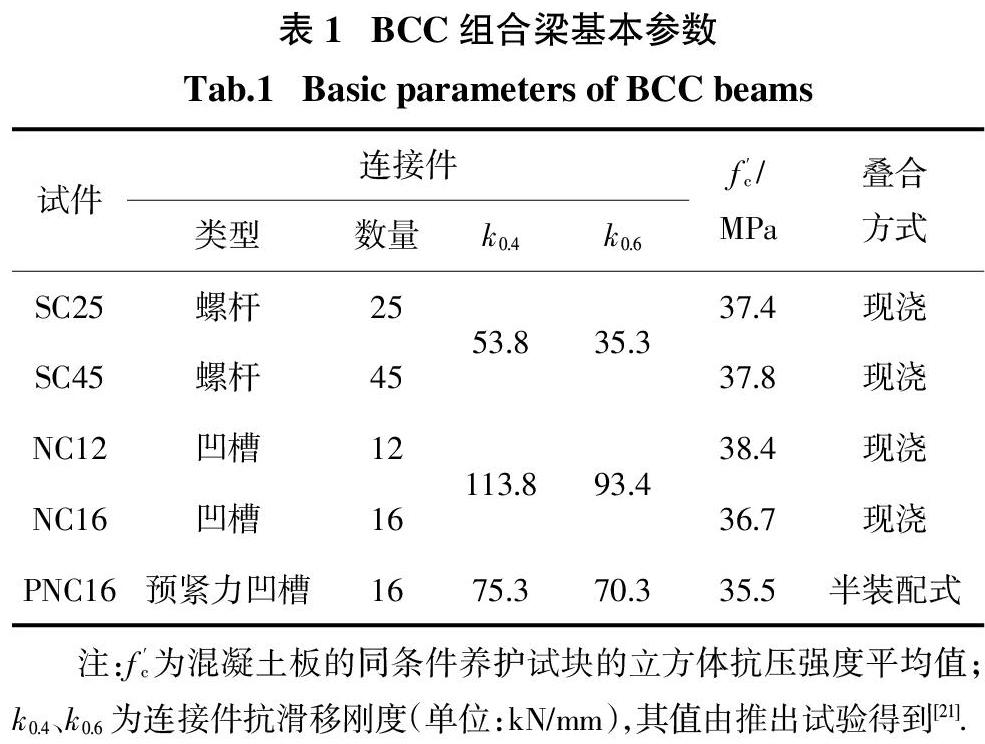
本文开展5根足尺BCC简支梁的抗弯试验，试件截面形状均为T型，设计尺寸如下：上部混凝土板为8 000 mm×900 mm×100 mm（长×宽×高）;下部胶合竹梁为8 000 mm×112 mm×380 mm（长×宽×高）. 选用螺杆连接件（SC）、凹槽连接件（NC）和半装配式预紧力凹槽连接件（PNC）用于组合梁的抗弯试验[21]. 各连接件设计详图如图1所示，其中SC为延性连接件，NC和PNC为脆性连接件[21]. 表1给出了各试件的基本信息，其中，试件命名方式由连接件类型与数量构成. 图2给出了各试件连接件布置的方式. 按照试验参数，5个试件可以分为3组：销连接组，包括SC25和SC45;凹槽连接组，包括NC12和NC16;装配方式组，包括PNC16和NC16.

1.2   胶合竹梁

本文采用的胶合竹梁由4层胶合竹单板经指接、层叠、冷压胶合而成. 标准规格的胶合竹单板尺寸为2 440 mm × 1 220 mm × 28 mm（长×宽×厚）. 单板的力学性能参照木材相关测试标准[24-28]进行材料性能测试，得到的力学性能如表2所示.

由于胶合竹板尺寸较小，下部胶合竹梁需要通过指接接长到达设计长度. 指接头长度为100 mm，各层单板之间的接头错位布置，其原则为相邻指接头的间距不小于200 mm.

1.3   混凝土板

混凝土板设计强度等级为C30，配合比（质量比）为：水泥 ∶ 砂 ∶ 石 ∶ 水 = 1 ∶ 1.90 ∶ 3.10 ∶ 0.56，与组合梁同条件养护的标准立方体试块（150 mm×150 mm×150 mm）抗压强度平均值f′ c列于表1中. 为提高混凝土板的抗裂能力，板中布置HRB335Φ6@90 mm×90 mm的分布钢筋，保护层厚度为15 mm.

对于SC系列和NC系列的试件，采用现浇混凝土板，连接件直接锚固在混凝土板中，如图1（a）和1（b）所示. 而对于PNC试件，其上部采用带预留孔的预制混凝土板，现场装配完成后，采用现浇混凝土填充预留孔，通过扭力扳手拧紧螺帽施加预紧力，将混凝土板与竹梁装配在一起，如图1（c）所示.

2   试验方法及加载设备

抗弯试验采用四点加载，即梁两端简支，对应净跨l为7 800 mm，跨中荷载经分配梁传递到两个间距为2 000 mm加载点，如图3所示. 荷载由30 t液压油缸施加，另外，为防止组合梁在加载过程中侧翻，在靠近梁两端位置分别设置一对侧向支撑.

试验主要测量组合梁加载点处的荷载、跨中挠度和组合梁端部连接件的相对滑移. 上述荷载由力传感器测量，跨中挠度和纵向滑移分别由量程为125 mm和30 mm的LVDT测量. 其中，纵向LVDT通过钢角标固定在竹梁侧面，如图3所示. 试验过程中的荷载、挠度和滑移均采用DH3825数据采集系统自动记录，采样间隔为1 s.

加载制度按EN 26891—1991[29]进行，即加载到0.4Fest （预估承载力）时，持荷30 s，卸载到0.1Fest，持荷30 s，最后加载到组合梁破坏. 其中，Fest按欧洲规范EC5[23]中的等效刚度法进行估算.

3   试验结果

依据《木结构设计标准》（GB 50005—2017）[30]，将组合梁的跨中挠度达到l/250定义为正常使用极限状态（SLS），其对应的荷载为2Fs（两个加载点的荷载之和）;将组合梁的到达峰值荷载定义为承载力极限（ULS），对应荷载为2Fu. 本文试验所测的相关数据列于表3中.

3.1   破坏模式

对于SC类试件，在跨中挠度到达l/250（SLS）前，试件没有出现明显的破坏现象;而此后，随着荷载的增加，靠近跨中的指接头的胶缝从梁底向上产生开裂，并伴随清脆的开裂声;最终，当荷载达到峰值时，胶合竹梁在该指接头截面位置发生整体断裂，并伴有巨大的声响，具有明显的突然性，如图4（a）所示. 试验结束后，端部螺杆在组合界面处没有观察到明显的塑性铰，如图4（b）所示.

对于NC类和PNC类试件，在跨中挠度到达l/250（SLS）前，试件没有出现明显的破坏现象;此后，随着荷载逐步增大，端部凹槽中的混凝土出现斜裂缝，如图4（c）所示;达到荷载峰值时，端部连接件破坏，荷载出现较大幅度降低，伴随着相邻连接件凹槽出现开裂，荷载出现一定程度的恢复，这应该是剩余连接件之间产生了较为明显的剪力重分布[31];此后，随着连接件沿跨中逐个破坏，对应的荷载产生波動，最终在靠近跨中的指接头截面竹梁断裂，试验中止. 试验后破碎混凝土，可发现端部凹槽中的螺杆产生明显的塑性变形，如图4（d）和（e）所示.

3.2   荷载-跨中挠度曲线

图5给出了各试件的荷载-跨中挠度曲线，图中，两条直线分别对应于组合梁完全组合（上界限）与无组合（下界限）. 相关计算方法见第4节.

从图5可以看出，各组试件的荷载-跨中挠度曲线上升段特征基本一致，即跨中挠度达到l/250（SLS）前，荷载-跨中挠度近似成线性关系;而此后，荷载-跨中挠度曲线斜率逐步降低，最终与下界限基本平行，意味着组合效应持续下降，直至基本稳定. 主要原因应该是连接件的变形导致界面滑移，从而降低了组合效应，而连接件屈服后塑性变形则对应于组合效应的稳定状态.

当组合梁达到峰值荷载后：SC25和SC45的竹梁拉断，组合梁的承载力完全丧失，试件即刻失效，因此，SC类组合梁极限承载力由胶合竹梁在指接头处的抗拉性能控制;而对于NC12、NC16和PNC16试件的荷载-跨中挠度曲线在峰值荷载后均出现了较为明显的荷载恢复现象，对应于剩余连接件的剪力重分布. 因此，NC和PNC这两类组合梁的极限承载力主要由端部连接件的抗剪切强度控制.

对相同类型的组合梁，增加连接件的数量可以显著提升组合梁的刚度和承载力. 如SC45相比SC25，组合梁的极限承载力（2Pu）增加约1.3倍. 另外，从图5（b）中可以发现，NC16和PNC16两者的荷载-挠度曲线较为接近，两者的极限承载力差异仅为4%. 考虑到PNC装配施工的效率更高，故半装配式的PNC连接件优势明显.

3.3   荷载-滑移曲线

图6为各试件端部连接件的荷载-滑移曲线. 由图6可以看出，对于同种连接件，端部滑移量随连接件数量的增加而减少，这意味着连接系统的抗剪切刚度退化小，故增加连接件的数量可提高组合效应.

根据已经完成的推出试验[21]，得到SC、NC和PNC 3种连接件的荷载-滑移本构，如图7所示. 在图7的曲线上标出了各组合梁试件端部连接件的最大滑移su和由推出试验测得的连接件的破坏滑移smax[21].

可以发现，SC25和SC45试件端部连接件的su虽然处于塑性段，但显著低于其极限滑移smax（10 mm），这主要是胶合竹梁在指接部位过早失效，导致SC类连接件的力学性能没有充分发挥. 因此，改善胶合竹梁指接头的加工质量，提升指接头的抗拉强度，对于提高SC组合梁的抗弯性能具有重要意义.

对于NC和PNC试件，其端部连接件的su均超过了其对应的smax，对应图5（b）中的试件峰值荷载后的承载力恢复现象，验证了连接件发生了较为显著的剪力重分布这一推断.

4   结果分析与讨论

4.1   组合效应

组合效应主要反映BCC中胶合竹梁与混凝土板之间的约束程度. 其上界限为完全组合效应，即梁、板无相对滑移，组合梁仅一条中和轴，满足平截面假定;其下界限为无组合效应，即梁、板之间可自由滑动. 本文中组合效应（DCA）按下式计算[31]：

式中：ΔR为跨中挠度;ΔN为无组合效应的计算挠度;ΔF为完全效应下的计算挠度.

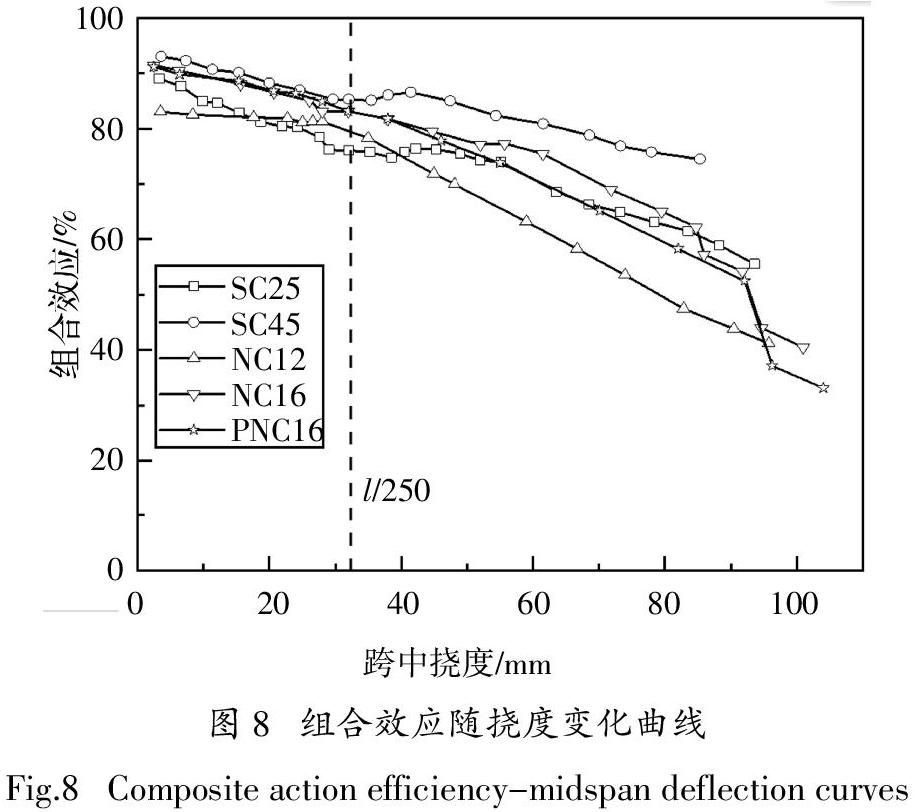
各试件的组合效应随挠度变化曲线如图8所示. 在加载初期，除了NC12外，其余试件组合效应较高，平均初始组合效应DCAint超过92%. 在SLS状态下，SC25组合效应下降幅度最为明显，SLS下的DCAsls相对DCAint降低了约15%. 其余4根试件的组合效应下降幅度相对较小，均低于8%，表明其抗弯性能较为稳定. 随着挠度增加，除SC45外，其余组合梁的组合效应下降速率（对应于曲线斜率）基本一致. 相对而言，SC45的组合效应最为稳定，这应该与该试件的连接件数量多，且滑移量小有关. 此外，对比PNC16与NC16，两者的DCAint、DCAsls及退化曲线均很接近.

需要说明的是，组合效应与界面的相对滑移量直接相关，因而，通过在跨中截面布置应变片，测量混凝土板底部和胶合竹梁顶部处的应变差异，可以直接考察组合梁的组合效应[10]. 在相同条件下，组合界面两侧应变差异越大，则组合效应越小. 本文缺乏混凝土板与胶合竹梁的应变测量数据，组合效应的讨论源于推出，存在一定的不足，将在后续试验研究中予以补充.

4.2   抗弯承载力预测

目前，TCC梁的设计主要是参照欧洲规范EC5中的等效刚度法[23]，该方法引入连接件的抗滑移刚度和间距，以考虑界面连接件对组合梁的影响程度. 即引入折減系数γc，对组合梁的截面刚度进行等效换算，故简称γ法. 等效截面抗弯刚度（EI）ef的计算公式如下：

式中：下标t、c分别表示混凝土板和木梁;I、A、E分别表示惯性矩、截面面积和弹性模量;γc为连接件影响系数;ki为连接件割线刚度，分别取k0.4和k0.6[32]，其值查表1可得;s1为连接件有效间距;l为组合梁净跨;a为梁、板各自截面形心到组合梁截面形心的距离.

本文采用等效刚度法预测5根BCC梁在SLS和ULS下对应的承载力. 由于该方法中的公式是基于均布荷载作用而推导得到的，故按照跨中弯矩等效的原则，将试验测得的集中荷载值2Fs与2Fu分别换算成为均布荷载，作为qs和qu的试验值，分别列于表4中.

按照等效刚度法，组合梁在SLS下的qs按下式计算：

如前所述，SC类试件的极限承载力由胶合竹在指接截面的抗拉强度控制，则其ULS下的承载力qu按下式计算得到[10]：

式中：σm和σn分别为跨中截面胶合竹梁底部的弯曲应力和拉伸应力;fm和fn分别为胶合竹的抗弯和抗拉强度设计值，分别取52.9 MPa和35.6 MPa[3].

NC和PNC系列试件承载力qu由端部连接件的抗剪切强度控制，计算公式如下[23]：

式中：s为端部连接件间距，即端部连接件距支座的距离加上其与相邻连接件间距的一半;Fmax为连接件的最大承载力[21].

表4给出了等效刚度法的预测结果与试验值的对比结果. 可以看到该法高估了BCC梁的承载力. 在SLS下，计算误差为13%～34%，平均误差约为19%，胶合竹材料性能的波动及指接头对抗弯截面的削弱，可能是误差的主要来源. 在ULS下，计算误差为8%～44%，平均误差约为24%，其主要原因应该是跨中区域指接头的提前失效导致胶合竹梁在该位置处整体断裂，这对SC类试件的极限承载力计算误差的影响尤为显著.

相对而言，等效刚度法对NC和PNC试件的极限承载力计算误差相对较小，其原因是这些试件的极限承载力主要由端部连接件的抗剪切强度控制，而非胶合竹梁的抗拉性能控制，受指接头的影响相对较小. 其计算误差可能主要来自于等效刚度法的线弹性假设，而连接件的破坏具有明显的塑性变形特征（图5（d）～5（e）），这与线弹性假设有明显出入[10].

综上所述，直接采用欧洲规范EC5中的等效刚度法预测BCC梁的抗弯承载力并不合適，有必要考虑指接头的削弱以及连接件的塑性变形对等效刚度法的折减，这方面需要开展进一步研究.

5   结   论

本文研究了3种连接件的胶合竹-混凝土组合梁基本抗弯性能，得到的主要结论如下：

1）BCC梁具有较高的初始组合效应，且在正常使用极限状态前的组合效应相对稳定，具有良好的抗弯性能.

2）对于采用销连接件（SC）的BCC梁，其极限承载力由指接部位竹材的抗拉强度控制;而对于采用凹槽类连接件（NC和PNC）的BCC梁，其极限承载力主要取决于端部连接件的抗剪切强度.

3）对于同种连接件，增加连接件数量可以有效提升BCC梁的抗弯刚度和承载力.

4）采用PNC连接件的半装配式BCC梁与现浇施工方式的NC组合梁相比较，抗弯性能很接近. PNC梁具有更高的施工效率和较低的人工费用，其具有良好的应用前景.

5）欧洲规范EC5中的等效刚度法明显高估了BCC梁的承载力，不适合直接套用于BCC梁，有必要考虑指接头的削弱以及连接件塑性变形的影响，这方面需要开展进一步研究.

参考文献

[1]    于文吉. 我国重组竹产业发展现状与趋势分析[J]. 木材工业，2012，26（1）：11—14.

YU W J. Current status and future development of bamboo scrimber industry in China[J]. China Wood Industry，2012，26（1）：11—14. （In Chinese）

[2]    CHEN F M，JIANG Z H，WANG G，et al. The bending properties of bamboo bundle laminated veneer lumber （BLVL） double beams[J]. Construction and Building Materials，2016，119：145—151.

[3]    XIAO Y，SHAN B，CHEN G，et al. Development of a new type glulam-glubam[C]//Proceedings of the First International Conference on Modern Bamboo Structures （ICBS）. Changsha：CRC Press，2007：41—50.

[4]    肖岩，单波. 现代竹结构[M]. 北京：中国建筑工业出版社，2013：13—47.

XIAO Y，SHAN B. Glubam structures[M]. Beijing：China Architecture & Building Press，2013：13—47. （In Chinese）

[5]    XIAO Y，YANG R Z，SHAN B. Production，environmental impact and mechanical properties of glubam[J]. Construction and Building Materials，2013，44：765—773.

[6]    单波，周泉，肖岩. 现代竹结构技术在人行天桥中的研究与应用[J]. 湖南大学学报（自然科学版），2009，36（10）：29—34.

SHAN B，ZHOU Q，XIAO Y. Research and application of modern bamboo structure pedestrian bridge[J]. Journal of Hunan University（Natural Sciences），2009，36（10）：29—34. （In Chinese）

[7]    XIAO Y，ZHOU Q，SHAN B. Design and construction of modern bamboo bridges[J]. Journal of Bridge Engineering，2010，15（5）：533—541.

[8]    YEOH D，FRAGIACOMO M，DE FRANCESCHI M，et al. State of the art on timber-concrete composite structures：literature review[J]. Journal of Structural Engineering，2011，137（10）：1085—1095.

[9]    LUKASZEWSKA E. Development of prefabricated timber-concrete composite floors[D]. Lulea：Lulea University of Technology，2009：7—33.

[10]  YEOH D. Behaviour and design of timber-concrete composite floor system[D]. Christchurch：University of Canterbury，2010：136—165.

[11]  KHORSANDNIA N，VALIPOUR H R，CREWS K. Experimental and analytical investigation of short-term behaviour of LVL-concrete composite connections and beams[J]. Construction and Building Materials，2012，37：229—238.

[12]  FRAGIACOMO M，AMADIO C，MACORINI L. Short-and long-term performance of the “Tecnaria” stud connector for timber-concrete composite beams[J]. Materials and Structures，2007，40（10）：1013—1026.

[13]  AUCLAIR S C，SORELLI L，SALENIKOVICH A. Simplified nonlinear model for timber-concrete composite beams[J]. International Journal of Mechanical Sciences，2016，117：30—42.

[14]  DIAS A M P G. Mechanical behavior of timber-concrete composite joints[D]. Delft：Delft University of Tecnology，2005：10—24.

[15]  ZHU W X，YANG H F，LIU W Q，et al. Experimental investigation on innovative connections for timber-concrete composite systems[J]. Construction and Building Materials，2019，207：345—356.

[16]  JIANG Y C，HONG W，HU X M，et al. Early-age performance of lag screw shear connections for glulam-lightweight concrete composite beams[J]. Construction and Building Materials，2017，151：36—42.

[17]  SHI B K，ZHU W X，YANG H F，et al. Experimental and theoretical investigation of prefabricated timber-concrete composite beams with and without prestress[J]. Engineering Structures，2020，204：109901.

[18]  贺国京，冷骏，杨传建，等. 木-混凝土组合梁变形计算的修正折减刚度法[J]. 建筑结构，2017，47（17）：24—28.

HE G J，LENG J，YANG C J，et al. Modified reduction stiffness method for calculating deflection of timber-concrete composite beam[J]. Building Structure，2017，47（17）：24—28. （In Chinese）

[19]  单波，梁龙辉，肖岩，等. 胶合竹-混凝土复合式凹槽连接性能的试验研究[J]. 工业建筑，2015，45（4）：18—25.

SHAN B，LIANG L H，XIAO Y，et al. Experimental research on notched connection for glubam-concrete composite beams[J]. Industrial Construction，2015，45（4）：18—25. （In Chinese）

[20]  單波，王震宇，肖岩，等. 胶合竹-混凝土组合梁销栓连接性能试验研究[J]. 湖南大学学报（自然科学版），2018，45（1）：97—105.

SHAN B，WANG Z Y，XIAO Y，et al. Experimental research on dowelled connection of glubam-concrete composite beams[J]. Journal of Hunan University（Natural Sciences），2018，45（1）：97—105. （In Chinese）

[21]  SHAN B，XIAO Y，ZHANG W L，et al. Mechanical behavior of connections for glubam-concrete composite beams[J]. Construction and Building Materials，2017，143：158—168.

[22]  魏洋，吳刚，李国芬，等. 新型FRP-竹-混凝土组合梁的力学行为[J]. 中南大学学报（自然科学版），2014，45（12）：4384—4392.

WEI Y，WU G，LI G F，et al. Mechanical behavior of novel FRP-bamboo-concrete composite beams[J]. Journal of Central South University（Science and Technology），2014，45（12）：4384—4392. （In Chinese）

[23]  Eurocode 5  design of timber structures-part 1-1：general-common rules and rules for buildings：EN 1995-1-1：2004[S]. Brussels：Committee European Normalisation，2004：112—115.

[24]  木材密度测定方法：GB/T 1933—1991[S]. 北京：中国标准出版社，1991：1—4.

Method for determination of the density of wood：GB 1933—1991[S]. Beijing：China Standard Press，1991：1—4. （In Chinese）

[25]  木材顺纹抗压强度试验方法：GB/T 1935—2009[S]. 北京：中国标准出版社，2009：1—6.

Method of testing in compressive strength parallel to grain of wood：GB/T 1935—2009[S]. Beijing：China Standard Press，2009：1—6.（In Chinese）

[26]  木材抗弯强度试验方法：GB/T 1936.1—2009[S]. 北京：中国标准出版社，2009：1—6.

Method of testing in bending strength of wood：GB/T 1936.1—2009  [S]. Beijing：China Standard Press，2009：1—6. （In Chinese）

[27]  木材抗弯弹性模量测定方法：GB/T 1936.2—2009[S]. 北京：中国标准出版社，2009：1—5.

Method for determination of the modulus of elasticity in static bending of wood：GB/T 1936.2—2009[S]. Beijing：China Standard Press，2009：1—5. （In Chinese）

[28]  木材顺纹抗拉强度试验方法：GB/T 1938—2009[S]. 北京：中国标准出版社，2009：1—5.

Method of testing strength parallel to grain of wood：GB/T 1938—2009[S]. Beijing：China Standard Press，2009：1—5.（In Chinese）

[29]  Timber structures joints made with mechanical fasteners-general principles for the determination of strength and deformation characteristics：EN 26891—1991[S]. Brussels：Committee European Normalisation，1991：2—8.

[30]  木结构设计标准：GB 50005—2017 [S]. 北京：中国建筑工业出版社，2017：13—23.

Standard for design of timber structures：GB 50005—2017[S]. Beijing：China Architecture & Building Press，2017：13—23. （In Chinese）

[31]  GUTKOWSKI R，BROWN K，SHIGIDI A，et al. Laboratory tests of composite wood-concrete beams[J]. Construction and Building Materials，2008，22（6）：1059—1066.

[32]  YEOH D，FRAGIACOMO M，DE FRANCESCHI M，et al. Experimental tests of notched and plate connectors for LVL-concrete composite beams[J]. Journal of Structural Engineering，2011，137（2）：261—269.