基于改进IMK恢复力模型的钢筋混凝土柱参数识别与应用
2021-02-21郭玉荣龙沐恩
郭玉荣 龙沐恩

摘 要:提出了一种利用钢筋混凝土柱拟静力试验数据识别改进IMK模型骨架曲线参数,进而提高钢筋混凝土框架结构非线性模拟精度的方法. 通过引入可抗差的基于奇异值分解的无迹卡尔曼滤波算法(抗差SVD-UKF算法),抑制观测值粗差对参数识别的影响,采用粒子群算法对初始协方差矩阵、过程噪声矩阵和测量噪声矩阵进行自动寻优,在MATLAB中实现了柱滞回特征正负向对称与非对称两种情况下改进IMK恢复力模型骨架曲线参数的识别. 钢筋混凝土柱实测滞回曲线的模型骨架曲线参数识别结果及其在框架结构非线性模拟中的应用结果验证了本文方法的有效性.
关键词:恢复力模型;滞回特征;参数识别;抗差SVD-UKF算法;粒子群算法
中图分类号:TU317 文献标志码:A
文章编号:1674—2974(2021)01—0126—09
Abstract:A method for identifying the backbone curve parameters of the modified Ibarra-Medina-Krawinkler (IMK) model by using quasi-static test data of reinforced concrete columns and thus improving the simulation accuracy of reinforced concrete frame structures is proposed in this paper. In this method, a robust unscented Kalman filtering algorithm based on singular value decomposition(robust SVD-UKF algorithm) is introduced to suppress the influence of gross error of the observation on the parameter identification, and the particle swarm optimization algorithm is adopted to automatically optimize the initial covariance matrix, the process and measurement noise matrices. The identification of backbone curve parameters of the modified IMK model is realized using MATLAB,in which the symmetric and asymmetric hysteresis behavior of the columns in the positive and negative direction is considered. The effectiveness of the proposed method is verified by model backbone curve parameter identification based on the measured hysteretic curves of reinforced concrete columns and its application in the nonlinear simulation of frame structures.
Key words:hysteretic model;hysteretic behavior;parameter identification;robust SVD-UKF algorithm;particle swarm optimization algorithm
鋼筋混凝土框架结构的地震响应混合模拟[1] 及其抗倒塌性能的分析,需要可有效模拟钢筋混凝土构件滞回特征[2]的恢复力模型及准确的模型参数. 塑性铰模型是框架结构非线性模拟常采用的一种模型,它不仅反映构件的力学特征,还与构件的材料、约束状况及空间布局密切相关. 几十年以来,塑性铰模型已有了飞速发展,Clough等[3]开发了双线性模型;Wen[4]提出了光滑的塑性铰模型;Takeda等[5]开发了三线性塑性铰模型. 但是上述常见模型不能充分考虑构件在循环往复荷载作用下的刚度和强度退化,影响了整体结构模拟分析的精确性. Ibarra等[6-7]开发了复杂的塑性铰模型即改进的IMK (Ibarra-Medina-Krawinkler)模型. 改进IMK模型作为一种以三折线为骨架曲线的塑性铰模型,引入了基于能量耗散的退化参数β,考虑了构件在往复荷载作用下的多种刚度和强度退化,相对于其他塑性铰模型,能够较好地对钢筋混凝土梁柱的滞回特征进行有效模拟. 但根据模型经验公式直接计算的改进IMK模型骨架曲线参数可能会存在明显的误差,从而影响框架结构地震响应模拟精度或导致结构抗倒塌性能分析产生较大误差,因此,在选择恢复力模型之后,模型参数的准确度成为影响结构体系模拟精度的主要因素之一. 为此,本文提出一种结合拟静力试验的混合模拟方法,先从框架结构中选取部分关键构件进行拟静力试验,然后基于构件实测滞回曲线对构件恢复力模型骨架曲线参数进行识别,最后将识别的参数用于更新结构中相同构件的恢复力模型参数,并进行整体结构非线性数值模拟. 在这一混合模拟方法中,模型参数识别是最关键的环节之一.
目前在土木工程领域广泛使用的参数识别方法主要有最小二乘估计法(Least Square Estimation,LSE)、扩展卡尔曼滤波法(Extended Kalman Filter,EKF)和无迹卡尔曼滤波法(Unscented Kalman Filter,UKF)[8],其中UKF算法以其高效性成为非线性参数识别的常用方法. 但UKF方法在实际运用时仍存在一些局限性,系统状态先验信息矩阵会因为观测粗差、系统噪声等不确定的因素失去正定性,中断滤波进程,观测粗差等因素还会影响滤波过程,影响收敛速度和识别结果;此外,在UKF方法中初始协方差矩阵及过程噪声和测量噪声矩阵的确定较为繁琐,但它们的取值却又决定着参数识别的准确性. 基于此,本文运用可抗差的基于奇异值分解的无迹卡尔曼滤波算法(robust unscented Kalman filtering algorithm based on singular value decomposition,抗差SVD-UKF算法)[9]来解决状态先验信息矩阵失去正定性的问题并抑制粗差等对滤波过程的影响,并通过粒子群算法对初始协方差矩阵及过程噪声矩阵和测量噪声矩阵进行自动寻优,采用MATLAB实现了改进IMK恢复力模型骨架曲线参数的识别. 通过基于陆新征等的框架柱拟静力试验数据[10]的模型参数识别以及对其整体框架结构拟静力试验结果[11]的模拟对比,来验证本文方法的有效性.
1 改进的IMK恢复力模型
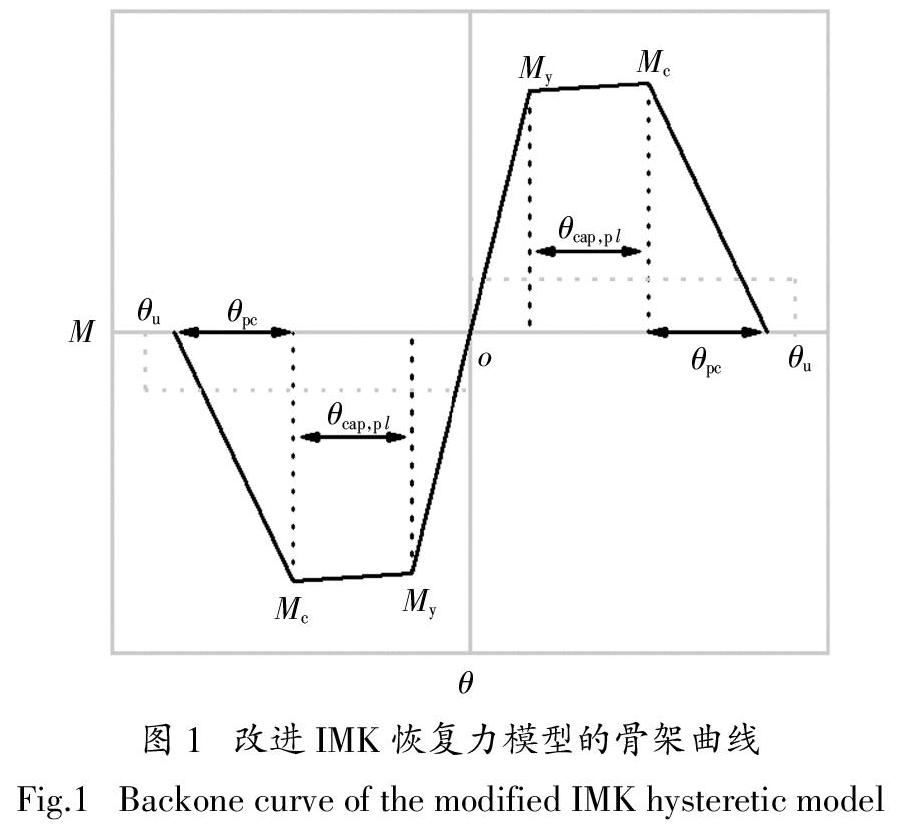
改进的IMK恢复力模型是一种用塑性铰来模拟梁柱构件非线性行为的恢复力模型,它采用三折线骨架曲线(如图1所示),其骨架曲线形状由5个参数EIy、θcap,p l、θpc、My、Mc /My确定,参数的计算如式(1)~式(5)[12]所示,其循环能量耗散能力λ的计算如公式(6)所示.
式中:EIy为割线模量;θcap,p l为塑性转角;θpc为峰值后转角;My为屈服弯矩值;Mc /My为屈服后硬化刚度;P/Ag f ′ c、ν均为轴压比;?准y和ky为由构件基本信息计算出的参数,在此不作展开;δ′= d′/d,d′为受压区边缘到受压钢筋中心的距离;s为塑性铰区的箍筋间距;asl为纵向钢筋滑移系数(考虑取1,不考虑取0);sn为钢筋屈曲系数,sn=(s/db)(fy /100)0.5,db为纵筋直径,fy为纵筋屈服强度;f ′ c为混凝土轴心抗压强度,单位为MPa;cunits是单位换算量,当f ′ c的单位为MPa时cunits取1;ρsh为柱塑性铰区的横向钢筋面积比;ρ为纵筋配筋率;b和d分别为柱横截面的宽度和高度.
2 无迹卡尔曼滤波算法
2.1 标准UKF算法
2.1.1 时间预测
利用第K-1步状态向量构造一组总数为2L+1的sigma点集,L为状态量的维度,X在本文中为待识别的参数 K1、K2、K3、 fy、 fp和恢复力r组成的状态向量:
2.2 抗差SVD-UKF算法
在观测粗差、计算机截断误差等因素的干扰下,状态协方差矩阵可能会失去正定性,导致无损变换(Unscented Transformation,UT)中的Cholesky分解失效. 本文采用SVD分解生成sigma點集,之后在UKF算法中通过抗差因子调节噪声矩阵来抑制观测粗差等因素对滤波过程的影响,该算法的流程图如图2所示.
2.2.1 抗差模型
抗差因子将观测值作为考量因素引入滤波过程中,起到动态调整测量噪声的作用. 采用观测残差构建抗差因子,抗差因子θk的表达式与IGGIII函数的形式相似,其表达式如下:
式中:k0、k1为阈值参数,k0通常取1.0 ~ 2.0,k1取3.0 ~8.5,本文中k0取1,k1取3;vk为当前步观测值与估计值的残差; vk为当前步观测值与估计值残差的均值;svk、σk分别为当前步观测值与估计值残差的标准化量和观测值与估计值残差的样本标准差.
2.2.2 SVD分解与观测协方差矩阵的调整
为了解决在异常情况下状态协方差矩阵失去正定性而无法使用Cholesky分解的问题,引入SVD分解计算sigma点集,计算公式如下:
2.2.3 粒子群算法的自动寻优
粒子群算法是模拟鸟群随机搜寻食物的捕食行为,鸟群通过自身经验和种群之间的交流调整自己的搜寻路径,从而找到食物最多的地点,其中每只鸟的位置为自变量组合,每次到达地点的食物密度即为函数值. 每次搜寻都会根据自身经验(自身历史搜寻的最优地点)和种群交流(种群历史搜寻的最优地点)调整自身的搜寻方向和速度,这称为跟踪极值,从而找到最优解. 粒子群算法的流程图如图3所示.
本文中定义粒子的位置为初始协方差矩阵的每个元素以及过程噪声和测量噪声矩阵的每个元素,即相当于构造了一个N维的空间,并让鸟群在这个N维空间中搜寻使适应度函数取值最小的坐标解,适应度函数为在每一个粒子自变量组合经过SVD-UKF算法识别参数后,由识别参数计算所得的每个恢复力值与相应试验值的残差平方和,残差平方和越大表示识别的结果越不可靠,反之则识别结果越可靠,也即粒子自身包含的自变量组合的取值越合理. 状态转移方程是表示粒子由当前时刻至下一时刻的位置变化方式,状态转移方程如下:
2.2.4 抗差SVD-UKF算法抗差效果分析
基于改进IMK三折线模型的MATLAB仿真,以表1参数为仿真参数值,通过输入位移峰值依次为4、10 、15 、20 、25 、30 、40 、45 、55 mm以及各级位移峰值循环两圈的加载序列,计算得到恢复力序列,之后为检验抗差效果将两类异常观测引入仿真结果.
1)单点异常:N(0,2Z(i)2)(均值为0,方差为2Z(i)2)的单点随机误差,其中Z(i)为当前恢复力值.
2)连续段异常:N(0,2Z(i)2)的连续段随机误差.
仿真结果加入异常后的观测值如图4所示,之后分别采用未抗差的UKF算法及抗差的SVD-UKF算法对加入异常的观测恢复力值进行滤波,滤波过程如图5所示.
图6为在引入单点异常后截取的2 000~4 000加载步的滤波过程图. 由图6可见,抗差算法的滤波过程跟真实值基本吻合,而未抗差算法的滤波过程受到单点异常影响而出现了偏离.
误差后截取的5 000~7 000加载步的滤波过程图. 由图7可知,抗差算法的滤波过程跟真实值基本吻合,而未抗差算法的滤波过程受到了连续段异常的影响而出现了较大波动.
可见,在两种异常的影响下抗差SVD-UKF算法拥有较强的鲁棒性与吻合程度.
3 低周反复荷载下钢筋混凝土柱的骨架曲线参数识别
3.1 试验概况
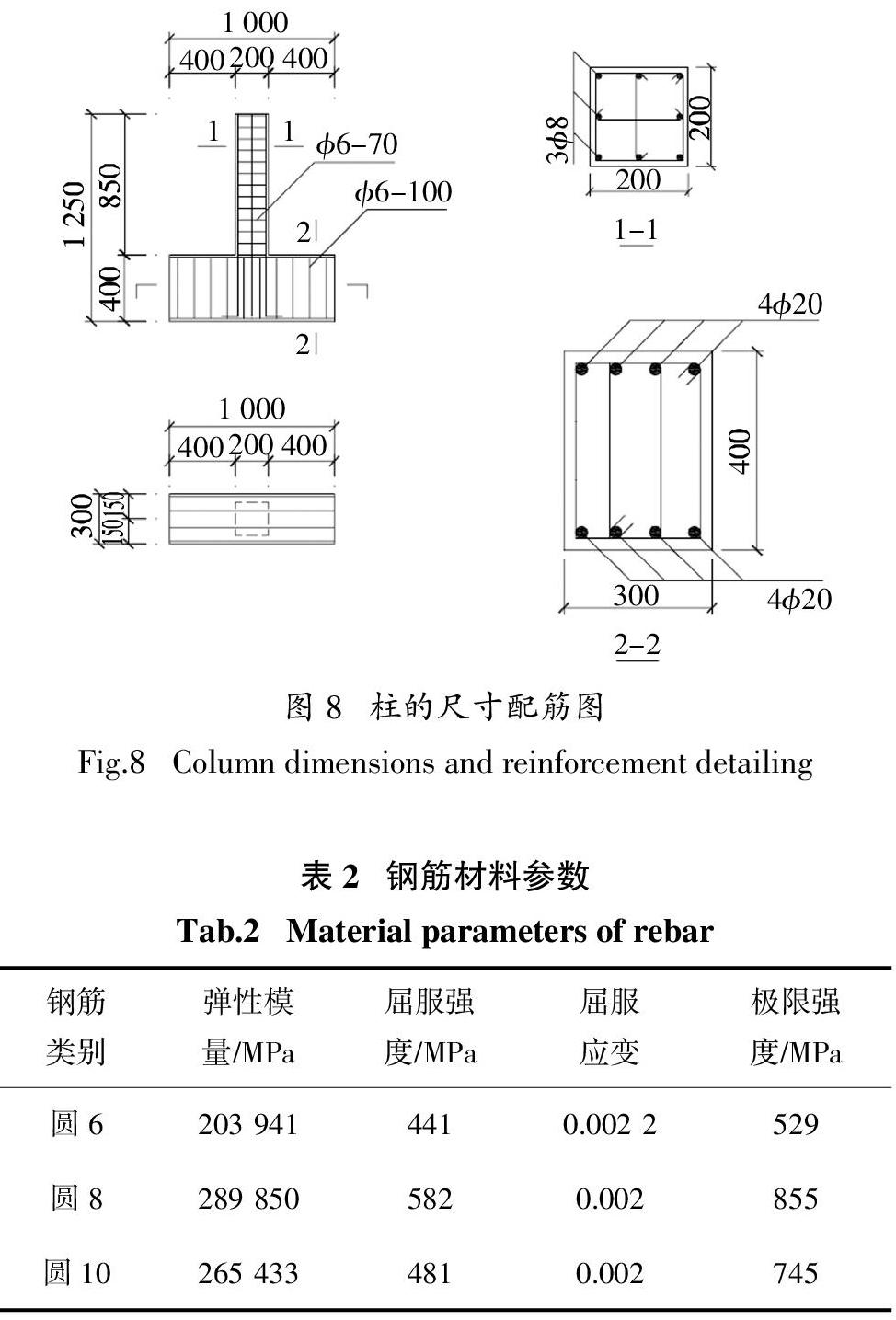
本文试验实测数据采自陆新征等[10-11]钢筋混凝土框架结构拟静力倒塌试验研究,试验包括一榀3层3跨整体框架的拟静力试验和一些关键构件的拟静力试验. 关键构件包括底层边柱和中柱各两个试件,层一的边节点和中节点各一个试件,本节参数识别选用了其中边柱A和中柱C的试验数据. 边柱A和中柱C的几何尺寸和配筋如图8所示,其中中柱角筋直径为10 mm,钢筋材料参数如表2所示,混凝土强度和对柱子施加的轴力如表3所示. 柱子拟静力试验的加载路径如下.
边柱A试验中首先施加柱端竖向荷载至试验轴压比,然后以水平荷载控制加载10 kN/级至30 kN,各级荷载循环一圈. 此后以水平加载点位移控制加载,所加水平位移峰值分别为10、15、20、25、30、37.5、45、55 mm,各级位移循环两圈.
中柱C试验中首先施加柱端竖向荷载至试验轴压比,之后以水平荷载控制加载10 kN/级至40 kN,各级荷载循环一圈. 此后以水平加载点位移控制加载,所加水平位移峰值依次为10、15、20、25、30、37.5、45、55 mm,各级位移循环两圈.
3.2 基于柱试验结果的改进IMK对称模型参数识别
本文采用抗差SVD-UKF算法,在MATLAB中编写了识别改进IMK对称模型骨架曲线参数的程序,识别参数包括弹性刚度K1、硬化刚度K2、退化刚度K3、屈服力fy和极限力fp这5个参数. 在后续的滞回曲线对比中,试验结果为柱子拟静力试验的实测滞回曲线;初始结果是指通过公式(1)~(6)计算得出改进IMK模型参数值后,依据柱子的位移加载路径计算得到的滞回曲线;以初始结果中计算得到的模型参数为参数识别的初始值,识别出5个待识别参数后,依据柱子的位移加载路径计算得到的滞回曲线称为识别结果.
边柱A的改进IMK模型骨架曲线参数的初始值和识别值对比如表4所示. 用初始值和识别值分别计算出柱子的滞回曲线,边柱A计算滞回曲线和试验滞回曲线的对比分别如图9和图10所示,与初始结果相比,识别结果与试验结果吻合较好,也即通过参数识别提高了模型参数的准确度.
图11为边柱A的试验结果、识别结果和初始结果的滞回环面积对比. 由图11的滞回環面积数据计算得到边柱A的识别结果滞回环总面积与试验结果滞回环总面积相差8.15%,边柱A初始结果滞回环总面积与试验结果滞回环总面积相差15.77%. 从滞回环总面积差来看,与初始参数相比,采用识别参数可以更好地模拟柱构件的滞回曲线.
3.3 基于柱试验结果的改进IMK非对称模型参数识别
在上述识别方法中,通过修改MATLAB中的程序,实现了改进IMK非对称模型骨架曲线参数的识别.
中柱C的改进IMK模型骨架曲线参数初始值和识别值对比如表5所示. 用初始值和识别值分别计算出柱子的滞回曲线,计算滞回曲线和试验滞回曲线的对比分别如图12和图13所示. 与初始结果相比,识别结果与试验结果吻合较好,也即通过参数识别提高了模型参数的准确度.
图14为中柱C试验结果、识别结果和初始结果的滞回环面积对比. 由图14的滞回环面积数据计算得到识别结果滞回环总面积与试验结果滞回环总面积相差26.03%,初始结果滞回环总面积与试验结果滞回环总面积相差31.79%. 可见,与初始参数相比,采用识别参数可更好地模拟柱构件的滞回曲线.
4 基于柱构件参数识别结果的应用
为检验基于柱实测滞回曲线的模型骨架曲线参数识别值的有效性,以下将识别的模型参数应用于整体框架结构的数值模拟,所选的框架结构来自陆新征等[10-11]完成的一榀3层3跨钢筋混凝土框架结构拟静力倒塌试验. 整体框架的数值模拟采用OpenSees建模,建模流程如下.
首先计算得到改进IMK模型的输入参数,然后在OpenSees中调用改进IMK模型并定义塑性铰材料,最后将材料用于梁柱端部零长度单元的弯曲特性,其余单元均为弹性梁柱单元. 柱端部改进IMK模型参数按两种工况取值换算,工况1采用由柱端截面的尺寸、材料、配筋、轴力等参数按照公式(1)~(6)计算得到的模型参数值;工况2采用基于柱实测试验数据得到的参数识别值,其中中柱的参数值选用中柱C负向的参数识别值,将参数识别值换算成模型参数值后,对割线刚度EIy、塑性转角θcap,p l和峰值后转角θpc根据框架的实际轴力按照公式(1)(3)(4)中轴压比的分项作了调整,考虑到屈服弯矩与轴压比关系的复杂性,对屈服弯矩My和屈服后硬化刚度Mc /My分别按公式(2)和公式(5)计算取值,对λ取一较大值,即不考虑构件的循环能量耗散. 之后,根据拟静力试验设定的加载路径,进行了两种工况下框架结构的数值模拟. 图15为两种工况下基底剪力-顶点位移数值模拟滞回曲线和试验滞回曲线的对比. 图16为工况1、工况2与试验结果的滞回环面积对比.
从图15曲线对比可以看出,工况1与工况2均对试验情况作出了较好的模拟. 由图16的滞回环面积数据计算得到基底剪力-顶点位移识别结果的滞回环总面积与试验结果的滞回环总面积相差23.71%,初始结果滞回环总面积与试验结果滞回环总面积相差36.50%. 从滞回环总面积差来看,与初始参数相比,采用识别参数可以更好地模拟框架结构的整体响应.
5 结 论
1)将抗差SVD-UKF算法运用于钢筋混凝土柱改进IMK模型的参数识别,有效抑制了观测粗差对识别进程的影响,并通过粒子群算法对初始协方差矩阵、过程噪声矩阵、测量噪声矩阵进行自动寻优,省去了大量的人力调参工作.
2)基于陆新征等[10-11]钢筋混凝土框架柱构件拟静力试验实测滞回曲线数据,对柱子的改进IMK模型骨架曲线参数进行了识别,结果表明识别参数精度较初始参数精度有明显提高.
3)将基于柱子试验数据识别的骨架曲线参数用于框架结构的拟静力加载试验数值模拟,结果表明利用识别参数可提高整体结构的数值模拟精度.
参考文献
[1] 郭玉荣,刘钟真. 基于OpenSees的子结构拟动力试验方法研究[J]. 湖南大学学报(自然科学版),2015,42(9):1—7.
GUO Y R,LIU Z Z. Research on substructure pseudo-dynamic test method based on OpenSees[J]. Journal of Hunan University (Natural Sciences),2015,42(9):1—7. (In Chinese)
[2] 過镇海. 钢筋混凝土原理[M]. 北京:清华大学出版社,1999:147—178,192—212.
GUO Z H. Reinforcement concrete theory[M]. Beijing: Tsinghua University Press,1999:147—178,192—212. (In Chinese)
[3] CLOUGH R W,JOHNSTON S B. Effect of stiffness degradation on earthquake ductility requirements[C]//Proceedings of the 2nd Japan earthquake engineering symposium. Tokyo,1966.
[4] WEN Y K. Method for random vibration of hysteretic systems[J]. Journal of the Engineering Mechanics Division,1976,102(2):249—263.
[5] TAKEDA T,SOZEN M A,NIELSEN N N. Reinforced concrete response to simulated earthquakes [J]. Journal of the Structural Division,1970,96(12):2557—2573.
[6] IBARRA L F,KRAWINKLER H. Global collapse of frame structures under seismic excitations [R]. California:Pacific Earthquake Engineering Research Center,2005.
[7] IBARRA L F,MEDINA R A,KRAWINKLER H. Hysteretic models that incorporate strength and stiffness deterioration [J]. Earthquake Engineering & Structural Dynamics,2005,34(12):1489—1511.
[8] 王涛,吴斌. 基于约束UKF模型更新的混合试验方法[J]. 地震工程与工程振动,2013,33(5):100—109.
WANG T,WU B.Hybrid testing method based on model updating with constrained unscented Kalman filter[J]. Journal of Earthquake Engineering and Engineering Vibration,2013,33(5):100—109. (In Chinese)
[9] 谭兴龙,王坚,李增科. 基于SVD的改进抗差UKF算法及在组合导航中的应用[J]. 控制与决策,2014,29(10):1744—1750.
TAN X L,WANG J,LI Z K. SVD aided improved robust UKF algorithm and its application for integration navigation [J]. Control and Decision,2014,29(10):1744—1750.(In Chinese)
[10] 陆新征,叶列平,潘鹏,等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅱ:关键构件试验[J]. 建筑结构,2012, 42(11):23—26.
LU X Z,YE L P,PAN P,et al. Pseudo-static collapse experiments and numerical prediction competition of RC frame structure Ⅱ:key elements experiment[J]. Building Structure,2012,42(11):23—26. (In Chinese)
[11] 陆新征,叶列平,潘鹏,等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅰ:框架试验[J]. 建筑结构,2012,42(11):19—22.
LU X Z,YE L P,PAN P,et al. Pseudo-static collapse experiments and numerical prediction competition of RC frame structureⅠ:RC frame experiment[J]. Building Structure,2012,42(11):19—22. (In Chinese)
[12] HASELTON C B,LIEL S,TAYLOR L,et al. Beam-column element model calibrated for predicting flexural response leading to global collapse of RC frame buildings[R]. California:Pacific Earthquake Engineering Research Center,2007.
