考虑参激振动的折线型立体桁架拱动力响应分析
2021-02-21贺拥军金志文周绪红
贺拥军 金志文 周绪红


摘 要:研究了拉索预应力折线型立体桁架拱中的拉索参激振动问题,使用ANSYS软件建立预应力拱有限元模型,分析了结构中拉索发生参激振动的可能性,采用非线性时程分析方法研究了结构在简谐加速度激励和地震作用下的动力响应,以及桁架拱拉索发生参激振动的诱发机制,考察了预拉力、激励幅值对拉索振动的影响. 研究结果表明:激励幅值一定,简谐激励频率与拱内侧拉索自振频率成2.05 ∶ 1关系时,将激发拉索的参激振动,拉索振幅较未发生参激振动时增加了约63倍,拱节点位移及杆件内力均有部分增加;地震波频率集中于拉索发生参激振动的频率范围时拉索有较大响应. 为保证预应力巨型网格结构在地震作用下的安全使用,需考虑拉索参激振动对结构的影响.
关键词:折线型立体桁架拱;拉索;参激振动;地震响应
中图分类号:TU393.3 文献标志码:A
文章编号:1674—2974(2021)01—0117—09
Abstract:The parametric vibration of cables in the pretensioned folded line type 3D-trussed arch was studied and the finite element model of pretensioned arch structure was established to investigate the possibility of parametric vibration of cable by utilizing ANSYS. The nonlinear time-history analysis method was adopted to study the dynamic response of the structures under different frequency harmonic load and seismic waves and to investigate the mechanism of parametric vibration of cable arch structure. The influence of parameters, such as the prestress and excitation amplitude, were investigated. The results indicated that the cable parametric vibration appeared when the ratio of the excitation frequency to the natural frequency of cable was 2.05 ∶ 1,the amplitude of cable increased by about 63 times and the response of some key nodes and members in the structure increased; the cable had a relatively large response when the frequency of the seismic wave concentrated on the frequency range in which the cable had a parametric vibration. The effect of cable parametric vibration on the structure response was necessary to be considered for ensuring the safety of the structure under earthquakes.
Key words:folded line type 3D-trussed arch;cable;parametric vibration;seismic response
近年来提出的预应力巨型网格结构[1-3],是在网格结构中布置预应力高强拉索而形成的一种刚柔组合空间结构体系. 预应力的引入有效地改善了结构的静力性能及稳定性,从而进一步提高了结构的跨越能力. 预应力拉索作为结构主要受力构件,具有大柔度、小质量、小阻尼的特点,在地震作用下呈现高度非线性,当结构的振动频率与拉索频率满足一定关系时,激发拉索的大幅度剧烈振动,拉索可能发生参激振动,引起拉索及其锚固端的破坏,导致拉索失效丧失承载力,最终影响空间结构的安全性及耐久性.
国内外针对工程中拉索的振动问题进行了系统性的研究. Irvine[4]对索的静力性能,动态响应做了深入探讨,研究了拉索在外力作用下的微分方程及求解方法;陈水生等[5]考虑拉索垂度及几何非线性导出了拉索在轴向激励下的非线性振动方程,指出发生参激振动时,激励频率与索的1阶频率比略大于2,论述了激励频率、激励幅值等因素对拉索参激振动的影响;赵跃宇等[6]研究了索-拱组合结构中斜拉索的非线性参激振动;Wu等[7]分别研究了斜拉桥在正弦激励、车辆荷载、地震作用下的拉索局部振动;于岩磊等[8]分析了斜拉网壳结构中拉索发生参激振动的可能性及影响因素;陈丕华等[9]在实验室觀测到了斜拉索的参激振动. 而作为新型结构体系的拉索预应力巨型网格结构,其拉索参激振动缺乏相应的系统性研究,要使其在实际应用中安全可靠,所做的研究工作还不够. 因此,对预应力巨型网格结构的非线性耦合参激振动现象及机理的进一步研究具有重要科学意义.
本文以拉索预应力折线型立体桁架拱为例,建立了结构有限元模型,研究了结构在简谐激励和地震作用下的基本性能以及拉索发生参激振动的条件与诱发机制,以期为预应力巨型网格结构的抗震设计提供理论依据.
1 拉索参激振动
参激振动[10]是除自由振动、受迫振动和自激振动以外的一种振动形式,由外界激励引发,激励不是以外荷载形式作用于系统,而是以参数的形式出现在振动运动方程中,并随时间变化. 当拉索端部横向激励频率与拉索的固有频率之比为1 ∶ 1时索发生主共振;拉索端部轴向激励频率与拉索固有频率之比约为2 ∶ 1时索易发生参激振动. 为研究预应力巨型网格结构的拉索振动机理,将拉索模型简化为单自由度非线性振动系统,如图1所示,索端部激励运动方程为Ux = U0 cos Ωt,其中Ω为外激励圆频率.
考虑重力平衡和小垂度建立索的振动微分方程[5]:
式中:H为索的初始径向拉力;h为索的径向动拉力;y为自重作用下的位移;v为偏离平衡位置的动力位移;m为索每延米质量. 取索的1阶振型函数[11]:
斜拉索面内位移激励1阶参激振动方程[5]可写为:
式中:ξ为拉索1阶振动模态阻尼比;ω1为考虑拉索垂度和几何非线性后索的1阶自振圆频率;α1为参激振动项系数,与外激励有关;α2为由垂度效应导致的平方非线性项系数;α3为大幅振动导致的立方非线性项系数;α4为外激励项系数,与外激励幅值和拉索倾角有关.
1.1 结构分析方法
1985年墨西哥城8.1级地震动时程曲线如图2(a)所示,由于软土地基的放大作用造成地震动强度放大,中低频成分强度增大,加速度峰值只有0.18 g,而且是周期约为2 s的简谐振动[12],其Fourier幅值谱图2(b)显示其频率集中于0.36~0.52 Hz,而在集中频率的外激励下,由文献[5]可知,拉索可能发生剧烈振动. 而大跨度拉索预应力网格结构在地震作用下,一方面,由于其显著的几何非线性效应,地震波起到了纵向激励的作用,在一定条件下可能引起结构中拉索的参激振动,致使结构竖向振动显著增大,甚至出现动力失稳;另一方面,拉索因其大幅度参激振动,反过来引起巨型网壳结构的振动特性和受力性能发生改变,对整体结构不利. 所以抗震设计中需要考虑参激振动的影响,以确保结构在地震作用下的安全性. 简谐荷载可以视为各种动力荷载的基本成分,而地震作用可以分解为不同频率、振幅、相位的简谐荷载的叠加,因此先对结构在简谐荷载作用下的动力响应进行分析,进而再研究结构在地震作用下的动力响应.
1.2 算例分析
以往对拉索参激振动的研究,多采用解析的方法对参激振动方程进行求解,而本文将探索拉索预应力巨型网格结构在动力荷载下的参激振动现象,作为高次超静定结构,建立解析模型的可行性较小,因此,本文采用有限元法对结构的参激振动进行数值分析. 对一水平拉索(如图3(a) 所示),考虑重力作用,分析在右端施加水平向位移激励时索跨中竖向振动特性. 拉索长l = 50 m、弹性模量E = 180 GPa、泊松比ν = 0.3、阻尼比0.001、预拉力F = 300 kN、截面面积A = 1 256 mm2、密度ρ = 7 850 kg/m3、屈服强度fy = 1 330 MPa. 拉索的模态分析结果显示其1阶自振频率f1为1.745 Hz,2阶自振频率f2为3.490 Hz,再在端部施加位移激勵Ux(t) = U0 sin(2πft),取激励幅值U0 = 0.02 m,激励频率f = 3.490 Hz,为拉索1阶频率的2倍,时间步长Δt = 0.01 s,共计40 s. 计算从结构的静力平衡状态开始,振动的初始位置不在原点,将各个节点初始位移值设为零,同时以索振动出现大幅度“拍”振现象为索发生参激振动的充分条件. 采用4阶龙格-库塔数值积分法求解微分方程(3),索跨中竖向位移如图3(b)所示,再采用有限元法通过ANSYS求解,用Link180单元模拟拉索,将索划分为50个等长单元,约束平面外自由度,拉索跨中竖向位移时程曲线如图3(c)所示.
图3(b)(c)显示拉索发生参激振动时跨中竖向位移时程均出现5个明显的“拍”现象,MATLAB解析解与ANSYS数值解振动峰值分别为0.75 m、0.72 m,误差为4.0%,两者计算结果基本吻合,说明ANSYS数值解的正确性与可靠性.
2 结构基本动力特性分析
2.1 结构分析模型
研究[1]表明,主结构在竖向荷载作用下,其失稳形态为主体在平面内发生竖向位移变形,桁架拱跨中向下凹,两端向上略凸,平面外未出现失稳情况,基于结构失稳形态,在拱跨中内侧和外侧布置拉索,使拉索与拱相交的位置大致处于拱屈曲反弯点上,在拉索与拱之间布置撑杆,结构形式如图4(a)所示. 采用ANSYS有限元软件进行分析,桁架杆、撑杆及预应力拉索均采用Link180单元,各单元之间假定为铰接,采用初始应变法对拉索施加预拉力,结构阻尼采用瑞利阻尼,阻尼比取0.02. 桁架拱跨度为120 m,桁架梁高度为3 m,撑杆长8 m,矢跨比为1/6,上弦网格数为6. 上下弦杆截面尺寸为Φ245×14,腹杆选用Φ152 × 10,拉索截面为Φ40,撑杆为Φ219×10. 钢材采用Q235B,屈服强度为235 MPa,弹性模量E =210 GPa,采用双线性等向强化模型(BISO 模型). 拱内侧拉索、外侧拉索预拉力分别为300 kN、200 kN,拉索阻尼比0.001,弹性模量E = 180 GPa,屈服强度1 330 MPa. 上弦所有节点承受15 kN竖向集中荷载. 桁架拱两端采用下弦固定铰支的支撑形式. 为简化分析,选取预应力巨型网格结构的一榀折线型立体桁架拱(Ⅰ-Ⅰ)进行分析,如图4(b)所示,约束节点平面外自由度,分析时考虑几何非线性.
2.2 基本动力特性分析
首先对结构进行模态分析,再对拉索单独进行动力特性分析. 表1列出了结构的自振频率及特征,图5为结构与拉索频率的对比. 由于结构的对称性,只列出了1~5号拉索的前2阶自振频率与整体结构的前10阶自振频率,可以看出整体结构的2阶频率(1.852 Hz)与最长的跨中内侧1号拉索的1阶频率(1.840 8 Hz)基本相等,结构的4阶频率(3.348 Hz)与1号索的2阶频率(3.684 Hz)相近. 根据频率匹配原则,可以判断跨中内侧拉索1发生参激振动的可能性最大.
3 简谐荷载作用下结构动力响应分析
为研究结构中拉索发生参激振动的条件与诱发机制,对结构施加简谐加速度A sin Ωt,其中A为加速度幅值,Ω为外激励频率. 由2.2节计算得到跨中内侧拉索1前2阶频率分别为1.840 8 Hz、3.684 1 Hz. 拉索1阶圆频率ω=2π×1.840 8 rad/s. 采用完全法瞬态分析,分别取激励频率比Ω/ω为0.3~3.0,加速度峰值A取为200 cm/s2,时间步长取0.01 s,计算时间为25 s. 结构关键节点及单元如图6所示,以索出现大幅度“拍”振现象为索发生参激振动的充分条件.
3.1 竖向激励下结构动力响应
3.1.1 不同频率比拉索关键节点振动特性
对结构施加竖向简谐加速度,图7为拱内侧1号拉索跨中15号节点,拱外侧4号拉索跨中12号节点竖向时程曲线最大值的频率响应曲线. 可以看出,当激励频率比为0.9~1.2时,外激励频率接近结构2阶频率(1.85 Hz),12号节点最大位移达到0.79 m;当外激励频率比为1.9~2.09时,跨中内侧索振幅急剧增大,拉索发生参激振动,频率比为2.05时1号索振幅达到最大值0.57 m,而未发生参激振动时的最小振幅只有0.009 m,振幅增加约63倍;当激励频率比在其他范围时,由于结构未发生共振及参激振动,1号拉索的响应均很小. 4号拉索其1阶频率为4.35 Hz,除激励频率比为1左右时有较大振幅外,12号节点未出现较大振幅.
3.1.2 拉索发生参激振动时的响应特性
深入研究激励频率比为2.05时1号拉索发生参激振动时的振动特性. 图8(a)为拉索15号节点竖向振动时程曲线,由于拉索阻尼和非线性的影响,在0~6 s内节点在平衡位置处小幅度振荡,最大振幅为0.04 m,从7 s开始振幅迅速增加,14 s达到峰值0.57 m,出现一个“拍”的现象,此后峰值略有减小,从19 s开始稳态振动,振幅基本稳定维持在0.48 m直至25 s计算结束. 由振动频谱曲线图8(b)可知,拉索发生了相对幅值较大的1阶振动. 图8(c)为1号索拉力时程曲线,拉索大幅度振动时引起张拉力发生改变导致拉索的频率偏离其原有频率,索节点位移最大值出现在激励频率比Ω/ω = 2.05而不是Ω/ω = 2.0. 图8(d)为索与撑杆交点13号节点的水平向振动频谱,频率集中在3.76 Hz,为索1阶频率的2.04倍,即在竖向外激励作用下,易激发拉索发生参激振动.
索-拱耦合振动作用表现为一个能量传递的过程,能量通过桁架拱、撑杆传递到拉索上,引起跨中内侧拉索发生参激振动,当拉索阻尼和非线性因素影响越来越大,外激励输入能量,拉索振动、恢复力作负功耗散能量平衡时,最终达到稳态振动. 值得注意的是当激励频率比为1左右時,结构发生共振,如图9所示,杆件迅速进入塑性导致整体结构下沉,而索跨中节点先剧烈振动,后振动幅度减小,由于桁架拱的下沉导致其竖向位移增大.
3.1.3 不同频率比杆件内力及拱节点竖向位移
由于过大的振动必然对结构造成危害,故需要对结构杆件内力及拱节点进行分析. 图6(b)拱x正向的单元20 ~ 32为正向立体桁架网格交叉部位和各网格中间部位下弦杆件. 单元杆件内力峰值图如图10所示. 由图10可知,由于结构自重的影响,靠近支座端部的轴力较大,而靠近跨中的内力先大幅减小,然后存在一定程度的增加. 当激励频率比Ω/ω = 1.0时,结构发生共振,支座端部杆件进入塑性,除拱顶杆件轴力略小于其他频率比下的反应以外,其他均为最大;当激励频率比Ω/ω = 2.05时,1号拉索发生参激振动,靠近支座端部杆件进入塑性,拱顶附近杆件轴力达到最大值,说明拉索大幅振动会增大相应位置处杆件内力.
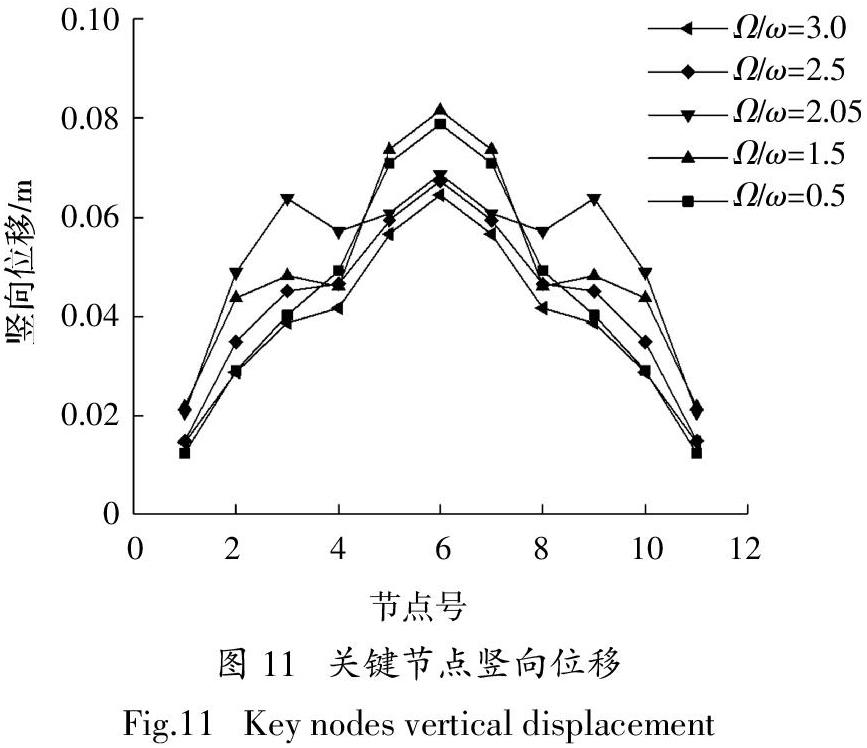
节点1至11为撑杆桁架连接处,索桁架连接处及拱关键位置节点. 图11显示节点竖向位移峰值从支座端部向跨中逐渐增大,到达拱顶时达到最大,当结构发生共振时,拱顶6号节点达到0.63 m时,为便于对比未列出;索发生参激振动时,索拱连接处与索撑杆连接处竖向位移均大于其他频率下的响应,但拱顶节点6未出现大幅振动,其原因是索的剧烈振动主要是影响靠近索端部的桁架拱.
以上现象说明外激励频率对结构存在影响,一旦激起结构共振或拉索的参激振动,均会增大相应杆件内力及节点位移,对结构造成不利影响.
3.2 水平向激励和双向激励下结构响应
仅对结构施加水平向简谐激励,如图12(a)所示,当激励频率比为Ω/ω = 0.5时,外激励频率0.920 4 Hz与结构1阶频率0.83 Hz相近,诱发结构共振,最终导致失效破坏,其他频率比下各单元内力相差不大. 从拉索1振幅及各关键点位移图12(b)和图12(c)可以看出,除结构发生共振时竖向位移较大以外,其余频率比下各关键点位移均很小,水平向简谐激励未能诱发拉索发生参激振动.
同时施加水平向和竖向简谐激励,激励频率比Ω/ω为2.05,索15号节点振幅如图12(d)所示,竖向位移略小于仅施加竖向简谐激励下的响应,即水平向激励对索发生参激振动有抑制作用. 对预应力拱,竖向激励的影响远大于水平向的激励,这是由于结构竖向刚度较弱导致的.
3.3 参数分析
3.3.1 预拉力的影响
考虑内侧拉索预拉力分别为100、200、300、400、500 kN,施加竖向简谐激励,激励频率为拉索发生参激振动时的3.77 Hz,其余参数均相同. 不同预拉力下1号拉索15号节点振幅最大值如表2所示.
预拉力对拉索振动有很大影响,除了预拉力为300 kN时,拉索发生参激振动竖向位移达到0.509 m以外,其余均是随着预拉力的增加而减小,其原因是预拉力改变了拉索的固有频率,而适当提高拉索的预拉力,有利于减小拉索在动荷载下的振动幅度.
3.3.2 外激励幅值的影响
对结构施加竖向简谐激励,激励频率为3.77 Hz,激励幅值分别为50、100、150、200、250 cm/s2,1号拉索15号节点最大振幅值如表3所示.
节点竖向位移随激励幅值的增加而先增加,后稍有降低. 即使外激励频率满足拉索发生参激振动的频率条件,也只有激励幅值达到一定程度时,才会引起结构拉索的参激振动.
4 地震作用下结构动力响应分析
第3节的研究结果显示,结构的拉索在特定频率下会发生参激振动,本节研究结构在地震作用下发生参激振动的可能性.
4.1 地震波输入
计算模型同第3节,选用抗震设防烈度为8度(0.2 g),罕遇地震,Ⅱ类场地,设计地震分组为2组,特征周期值为0.45 s,10条中硬场地天然地震波,以及采用三角级数法,控制频率范围及增量,拟合规范反应谱的频率较为集中的2条人工波作为地震波输入,所选的地震波列于表4,反应谱如图13所示,8度罕遇地震,将加速度峰值调整为400 cm/s2,仅考虑竖向地震波作用.
4.2 结构动力响应
1号拉索、桁架拱各节点位移峰值分别如图14(a)和14(b)所示. 索各关键点竖向位移均从端部向跨中逐渐增大;拱桁架节点竖向位移从两端向跨中先逐渐增加,在撑杆桁架交接处之后稍有降低,而后竖向位移继续增大,在跨中处达到最大值. 在6号地震波作用下,拱顶节点6、索跨中节点15竖向位移均最大,图14(c)显示6号地震动傅里叶谱在1.86 Hz左右的频率分量最为丰富,与结构2阶竖向振动频率基本一致,且与1号拉索1阶频率相近,易与结构产生“类共振”,导致结构响应最为强烈. 图14(d)为桁架各单元轴力,杆件轴力较为相近,人工波1作用下桁架拱靠近跨中处杆件内力最大.
人工波1、2 Fourier谱如图15(a)所示,人工波1卓越频率为3.83 Hz,为1号拉索1阶频率的2.08倍;拉索15号节点竖向位移时程曲线如图15(b)所示,由图15(b)可知,未出现图8(a)拉索发生参激振动时的剧烈振动,其原因是地震波频率较为分散地分布在3.64~3.98 Hz内,且激励幅值不断变化;人工波2卓越频率为5.66 Hz,为1号拉索频率的3.09倍,远离索的1、2阶频率,未能激起拉索的参激振动,桁架、索节点竖向位移均最小. 值得注意的是,激励频率靠近参激振动频率范围时较远离其频率范围时拉索有相对较大响应,即在特定条件下,拉索具有发生参激振动的可能性.
5 结 论
对预应力折线型立体桁架拱在简谐荷载和地震作用下的动力响应作了详细分析,得到以下结论:
1)拉索的大幅度非线性振动与折线型立体桁架拱是相关联的,拉索发生参激振动的可能性及振动特性有必要从加速度的角度在全结构中进行考虑.
2)无论是水平向还是竖向简谐激励,结构均存在明显共振现象. 竖向外激励频率约为结构中某拉索1阶频率的2倍时,易诱发拉索发生参激振动,拉索振幅较未发生参激振动时增加约63倍,杆件内力及桁架拱位移均有部分增加.
3)适当提高预拉力能减小拉索振动,激励频率和幅值均满足一定条件,才能激起拉索的参激振动.
4)地震波激励幅值和频率的不断变化会减小结构中拉索发生参激振动的可能性,但由于集中频率地震波的存在性,拉索预应力巨型网格结构抗震设计需要考虑参激振动的影响.
参考文献
[1] 贺拥军,章小桐,周绪红. 拉索预应力折线型立体桁架拱布索方案研究[J]. 湖南大学学报(自然科学版),2011,38(8):7—12.
HE Y J,ZHANG X T,ZHOU X H. Research on the arrangement styles of cables for pretensioned folded line type 3d-trussed arch[J]. Journal of Hunan University (Natural Sciences),2011,38(8):7—12. (In Chinese)
[2] 賀拥军,王继新,周绪红. 拉索预应力巨型网格结构布索形式研究[J]. 湖南大学学报(自然科学版),2017,44(7):1—6.
HE Y J,WANG J X,ZHOU X H. Research on arrangement styles of cables for prestressed reticulated mega-structures[J]. Journal of Hunan University (Natural Sciences),2017,44(7):1—6. (In Chinese)
[3] HE Y J,SUN X,WANG J X,et al. The elastic static property and stability of string cylindrical reticulated mega-structures[J]. Journal of Constructional Steel Research,2015,114:20—29.
[4] IRVINE H M. Cable structures [M]. Massachusetts:The MIT Press,1981:43—134.
[5] 陈水生,孙炳楠,胡隽. 斜拉索受轴向激励引起的面内参数振动分析[J]. 振动工程学报,2002,15(2):144—150.
CHEN S S,SUN B N,HU J. Analysis of stayed-cable vibration caused by axial excitation[J]. Journal of Vibration Engineering,2002,15(2):144—150. (In Chinese)
[6] 赵跃宇,吕建根. 索-拱组合结构中斜拉索的非线性参数振动[J]. 土木工程学报,2006,39(12):67—72.
ZHAO Y Y,LYU J G. Non-linear parametric vibration of cables in cable-arch composite structures[J]. China Civil Engineering Journal,2006,39(12):67—72. (In Chinese)
[7] WU Q,TAKAHASHI K,OKABAYASHI T,et al. Response characteristics of local vibrations in stay cables on an existing cable-stayed bridge[J]. Journal of Sound and Vibration,2003,261(3):403—420.
[8] 于岩磊,高维成. 大跨斜拉结构拉索参数振动有限元仿真分析[J]. 空间结构,2015,21(2):72—78.
YU Y L,GAO W C. Finite element simulation of parametric vibration of cables in long span cable-stayed spatial grid structures[J]. Spatial Structures,2015,21(2):72—78. (In Chinese)
[9] 陈丕华,王修勇,陈政清,等. 斜拉索面内参数振动的理论和试验研究[J]. 振动与冲击,2010,29(2):50—53.
CHEN P H,WANG X Y,CHEN Z Q,et al. Theoretical and experimental study on planar parametric oscillations in a stayed-cable[J]. Journal of Vibration and Shock,2010,29(2):50—53. (In Chinese)
[10] 刘延柱,陈立群. 非线性振动[M]. 北京:高等教育出版社,2001:152.
LIU Y Z,CHEN L Q. Nonlinear vibrations[M]. Beijing:Higher Education Press,2001:152.(In Chinese)
[11] TAGATA G. Harmonically forced,finite amplitude vibration of a string[J]. Journal of Sound and Vibration,1977,51(4):483—492.
[12] 袁麗侠. 场地土对地震波的放大效应[J]. 世界地震工程,2003,19(1):113—120.
YUAN L X. The amplifying effect of ground soil to earthquake wave[J]. World Earthquake Engineering,2003,19(1):113—120. (In Chinese)
