面向超级计算机系统的大规模图遍历优化

谭 雯，甘新标，白 皓，肖调杰，陈旭光，雷书梦，刘 杰

(1.国防科技大学 计算机学院，湖南 长沙，410073；2.湖南信息学院 通识教育学院，湖南 长沙，410217)

图在生物信息、社交网络、交通运输、天体物理等领域得到广泛应用，是大数据浪潮中的主要数据结构之一。许多现实问题可以抽象为图结构。随着大数据应用的发展，其问题的规模不断增长，对超级计算机平台的图存储运算能力产生了广泛需求。这些抽象图中的顶点数和相连的边数有时可以达到万亿级的规模，使得超级计算机系统被期望拥有更高的大数据存储和运算能力[1]。

为了评测超级计算机系统对大数据应用的运行能力，Graph500测试基准被提出，成为数据密集型计算机系统的评测工具。这一基准以图论来分析超级计算机在模拟生物、安全、社会以及类似复杂问题的吞吐量，成为超级计算机测试领域的一个新的主流测试基准。

大数据问题通常具有数据规模极大、数据密集度高、计算复杂性低、分布不均衡等特征。当将现实世界中的大数据问题抽象为图时，这些特征表现为图数据的小世界性(small-world)[2]和无尺度性(scale-free)[3]。小世界性是指在图的所有顶点中，任意两个图顶点的最短路径上的顶点数远少于图中顶点总数；无尺度性是指图中大部分顶点仅与少量顶点之间直接关联，即图中大部分顶点的度数较低。同时，存在少数顶点和数量庞大的顶点之间直接关联关系，即图中存在小部分度数非常高的顶点，这些顶点被称作高度数顶点。

为了应对现实世界中的大数据问题，高效地处理大规模图数据，基于图结构的小世界性和无尺度性的特征，笔者提出一种以顶点排序和优先缓存策略为基础的大规模图遍历优化方法。这一方法通过优化图结构的空间局部性来减少无效访存，提高访存带宽利用率。笔者的优化工作基于Graph500测试程序开展，并在天河超级计算机系统测试平台上进行测试，以检测并发挥天河超级计算机实验平台的图处理能力。

笔者的主要贡献如下：

(1)提出了以顶点排序和优先缓存策略为基础的大规模图遍历优化方法。这一方法将图中顶点按度数从高到低排序。在图遍历阶段，优先访问度数高的顶点；当条件满足时，及时中断访问，提升了击中概率，减少了进程间的无效通信，最大限度地避免了无效访存。同时将部分关键高度数顶点缓存至天河系统核组内的高速缓存中，使访问效率得到明显提升。

(2)将这一大规模图遍历优化方法应用于Graph500基准评测程序，在天河超级计算机系统测试平台上开展测试，通过全系统可用的904个节点，达到了2 547.13 GTEPS的稳定测试性能，超过Graph500国际榜单上排名第7名所达到的2 061.48 GTEPS的成绩。

1 相关工作

宽度优先遍历算法(BFS)是一种经典的图遍历算法。在Graph500测试基准中，宽度优先遍历算法是用于评测超算性能的核心遍历算法。这一算法以访存通信操作为主，能有效地发掘现实问题的抽象图结构中海量数据间的关联与延展，更好地模拟大规模图结构数据的数据密集型负载，对大数据应用问题的遍历搜寻更具备针对性。多年来，针对宽度优化搜索算法的优化，国内外的研究机构提出了一系列方案，并取得了长足进展。

AGARWAL等[4]提出采用位图结构来表示宽度优先遍历算法中的访问情况记录数组visit，大幅提升了单字节可表示的顶点访问信息数目，扩大了单个缓存行的有效数据量。UENO等[5]提出顶点按度数重新降序排序的优化策略，降低了查询时间，提高了cache命中率。BEAMER等[6]开创性地提出了一种方向优化的混合遍历优化算法，以尽可能地减少非必要遍历，大幅降低了访存通信开销。YASUI和FUJISAWA等研究者提出了度数感知优化策略，按度数拆分了顶点的邻接列表，对高度数顶点和非高度数顶点分开处理，并综合了前人的优化技术，大幅提高了Bottom-up算法的击中效率，有效地降低了通信次数[6]。UENO等[7]结合特定网络结构的特点，在通信方面开展优化，同时引入了数据压缩、混合搜索、顶点重排序等技术，达到了38 621.4 GTEPS的良好性能。

上述研究主要关注算法层面的优化。而在算法与体系结构的协同优化方面，BADER等[8]基于Cray MTA-2多节点平台，利用其提供的细粒度、低开销的同步操作支持，实现了多线程并行的宽度优先遍历优化算法，利用多线程来隐藏访存延迟，取得了较高的性能加速。清华大学的LIN等[9-10]面向“神威太湖之光”平台，通过模块流水映射、无竞争的数据混洗，基于组消息的批处理等关键技术的提出和应用，发挥了神威的硬件优势，在Graph500测试基准中获得了23 755.7 GTEPS的性能，并且在前述研究的基础上，应用了超节点路由、片上排序、度数敏感型通信等技术，进一步提出了通用图处理框架——“神图”结构。PENG等[11]和WOMBLE等[12]研究者，在Top500排名第2的Summit平台上，通过对Graph500标准程序应用数据压缩、混合搜索、度数排序、拓扑重组等技术，测试得到的结果处于世界先进水平。UENO等[7]基于日本“京”及其 “富岳”系统开发的Graph500优化程序，主要采用了数据压缩、混合搜索、顶点重排序、负载均衡以及基于Tofu网络结构的通信优化等技术，其性能表现多次登临Graph500基准榜首。而多位研究者面向天河二号平台，采用数据压缩、混合搜索、数据预取以及汇编优化等技术，以提升Graph500测试性能[13-14]。张承龙等[15]则面向高通量计算机系统，应用度数感知、顶点重排序、静态shuffle、基于快查找的位图访问等策略，取得了更高的处理能效。日本的研究者们基于富岳超级计算机系统的处理器结构和高性能网络，提出了针对性的通信优化策略，并对其性能表现进行了评估对比[16-18]。甘新标等[19-21]面向天河超算实验系统，应用图结构优化策略，在Matrix2000 CPU上使用SVE进行矢量化搜索，在专有互连网络上进行群组通信，以有效地发挥天河系统的图处理性能。

上述优化技术与相应研究，对超算平台上图遍历程序的优化研究具有重要的指导和借鉴意义。

2 Graph500

Graph500是评测超级计算机图处理能力的重要国际基准，它以每秒遍历的边数(Traversed Edges Per Second，TEPS)为性能指标，衡量超级计算机处理数据密集型应用的能力[22]。

2.1 基本流程

Graph500的基本流程如图1如示。

图1 Graph500流程图

图生成阶段，Graph500基准测试程序采用Kronecker生成器生成图数据。为了模拟现实问题的图结构，通过大量的统计分析验证，Graph500内置的Kronecker图生成器抽象了现实图的小世界性和无尺度性特征，其生成图的顶点分布呈现“长尾”现象。此阶段生成的图信息将以边元组列表形式存储，通常以邻接矩阵表示。Kronecker生成器有两个输入参数，分别是图规模因子Fscale和边因子Fedgefactor。Fscale表示生成图的规模为2Fscale，Fedgefactor表示每个图顶点的平均度数。默认情况下，Graph500的边因子Fedgefactor=16。假定Fscale=n，Fedgefactor=m，则生成图具有2n个顶点和m×2n条无向边[22]。

图构建阶段，生成图将进行重新构建，将边元组列表转化为特定的图结构表示。

图遍历阶段，Graph500提供了宽度优先遍历算法(Breadth First Search，BFS)和单元最短路径算法(Single Source Shortest Path，SSSP)两种遍历算法。其中，宽度优先遍历算法是一种更为经典的图遍历算法，能够有效地发掘现实问题的抽象图结构中海量数据间的关联与延展，更好地模拟大规模图结构数据的数据密集型负载，是笔者的主要研究目标。

图验证阶段，程序将按一定的规则，对图遍历阶段得到的生成树进行验证。如果验证有误，则中止程序。

Graph500中包含多个计时模块，仅将其中图遍历阶段的计时结果纳入最终性能指标Pteps的计算。假定Graph500在图遍历阶段的有效计时时间为t，Fscale=n，Fedgefactor=m，则Graph500评测性能为

Pteps=m×2n/t。

(1)

Pteps的单位为遍历的边数每秒(TEPS)，由图规模和搜索时间共同决定。图规模是Pteps的关键影响因素，但其主要取决于系统内存规模和图结构存储表示方法。笔者的优化研究重点关注影响Pteps的另一个关键因素，即宽度优先遍历算法的遍历时间。

2.2 生成图的幂律分布

图2为Fscale=30时的生成图的顶点度数分布图，得到图结构中的顶点度数近似符合幂律分布。

图2 顶点度数幂律分布图(Fscale=30)

图G=(V，E)包含顶点集合V和边集合E，通常使用vi表示图中编号为i的顶点，使用顶点对(vi，vj)表示顶点i到顶点j的边。(vi，vj)∈E，0≤i≤Nv-1，0≤j≤Nv-1，Nv为V中顶点个数。G通常用邻接矩阵A表示，如图3所示。图G的现实连接表示如图3(a)所示，图G的邻接矩阵表示如图3(b)所示。A中第i行第j列的元素Aij表示边(vi，vj)。Aij=1，表示vi与vj间存在相邻边；Aij=0，表示vi与vj间不存在相邻边。

图3 图的邻接矩阵表示

2.3 并行宽度优先遍历模块

基本的顺序宽度优先遍历算法描述如下：

(1)使用先进先出的队列Q管理顶点。vc表示当前顶点，vu表示待访问的vc的关联顶点，visited标识每个顶点的访问信息。visited[vu]=0，表示vu未被访问；visited[vu]=1，则表示vu已被其他顶点访问。

(2)使用一个队列表示顶点集合。每次迭代之初，从队首取出vc，并将本轮新访问的邻接顶点vu加入队尾，而后进行下一轮迭代。

(3)由于(2)中的迭代算法不利于并行化，因此考虑使用两个队列Q1，Q2。Q1用来保存当前迭代中用来拓展宽度优先遍历算法生成树的顶点，即上一轮迭代中访问到的顶点。Q2用来存储本轮迭代中访问并刷新状态的Q1中顶点的邻接顶点。等到Q1中顶点的所有邻接顶点全部访问完毕后，再将Q1与Q2进行交换，开展下一轮迭代搜索。如上，每轮的迭代相对独立，便于对同一层的顶点的宽度优先遍历进行并行化处理。

在Graph500基准测试程序的图遍历阶段，采用的并行化的宽度优先遍历算法描述如下：

(1)采用变量Fcur表示当前待搜索的顶点集合，Fnext表示下一层顶点搜索的顶点集合(即Fcur中顶点的所有邻接顶点)。

(2)开展检索之初，将根顶点vroot加入Fcur。

(3)从Fcur中的所有顶点开展遍历，取当前顶点vc的关联顶点vu进行判定。若该关联顶点此前未被访问，则更新其访问信息，并将该顶点加入Fnext集合。

(4)每轮迭代结束时，将Fnext赋给Fcur并将Fnext清空，再循环执行迭代，直至待搜索顶点集合Fcur为空。

代码1并行宽度优先遍历算法的伪代码。

输入：G(V，E)，vroot

输出：

①Fcur←ø

②Fnext←ø

③ for allvc∈V parallel do

④ visited[vc]=0

⑤ end for

⑥ visited[vroot]=1

⑦Fcur←vroot

⑧ whileFcur≠ø do

⑨ for eachvc∈Fcurparallel do

⑩ outputvc

在这一朴素的并行宽度优先遍历算法中，遍历仍处于盲目的完全搜索模式，如代码1的第11行for eachvu∈G.Adj[vc]parallel do中，程序需要逐一访问G中的顶点vu，来判定vu与顶点vc是否存在边关联，以确定顶点vc的关联顶点集合。即使某个顶点在一定条件下不存在未访问边，上述朴素算法仍需要通过例行访存来进行判定。考虑生成图的幂律分布特点，会存在相当多的无效访存。

3 以顶点排序和优先缓存策略为基础的大规模图遍历优化方法

从现实世界的大数据问题中抽象得到的图结构通常具有小世界性和无尺度性，并呈现出长尾效应。这种长尾效应的原因在于，现实世界得到的图数据中，顶点间度数差别很大，高度数顶点的计算、通信、存储的需求大，而低度数顶点的计算、通信、存储的需求小。基于长尾效应的存在，为了高效地处理大规模图数据，笔者充分利用度数高的关键顶点与其他顶点关联概率高的特性，对图中所有顶点按照度数高低从大到小进行排序，并对度数高于设定阈值的关键顶点进行优先缓存，最大可能地减少不必要的访存和对外通信，优化访存效率。

3.1 顶点排序算法

排序算法是高性能计算机体系结构的经典算法，应用广泛。常用的排序算法有冒泡排序、快速排序和归并排序等。为了能够更好地发挥国产飞腾众核处理器的计算性能，经前期理论分析和实验比较分析，归并排序既能充分发挥国产飞腾众核处理器的性能，又能大幅提升Graph500在天河超级计算机系统上的测试性能，适宜应用于本文中的优化程序。

归并排序是采用分治的策略先将待排序序列分成若干小的子序列，将各个子序列排序后，利用归并操作将各子序列逐步归并成有序序列。对于长度为N的序列，归并算法的时间复杂度为O(NlogN)，空间复杂度为O(N)。归并排序由于思想简单，速度较快，易于并行，常应用于众核加速[23]。

为了满足大规模科学工程计算与大数据处理等应用领域对高性能计算平台的需求，天河超级计算机系统设计了国产通用众核处理器，如图4所示。该众核处理器支持可变宽度的向量指令扩展。

图4 国产通用众核处理器体系结构

通用众核处理器全芯片由多个区域互连组成，每一个区域具有私有的处理器核心、高速缓存、外部存储接口和高速通信接口，可以看成是一个功能独立的处理器。多个区域通过互连，构成一颗处理器芯片。区域内部由多个核组通过区域内的互连接口组成，每个核组内包括多个处理器核心和共享的高速缓存，每个处理器核心为一组向量处理单元(Vector Processing Element，VPE)。通用众核集成外部存储接口和高速通信接口，为处理器核心的高性能计算处理提供相匹配的访存和通信能力。此外，片上还集成有PCI Express等标准IO接口，可直接连接标准外部设备，降低系统设计的复杂度。

为了将归并排序算法高效映射到国产通用众核处理器，笔者采用深度平衡归并策略[23]将每次归并排序优化映射分布到大量向量处理单元以完成向量并行加速。向量并行加速在第k级(最底层为第0级)将待排序的顶点划分为2个子序列，每个子序列划分成2k组，分别布置给2k个向量处理单元完成操作，最后各向量处理单元独立完成各自数据的归并。

3.2 顶点排序优化策略

基于顶点归并排序的VS-Graph500的测试流程包括如下步骤：图生成、图构建、基于顶点度数的预处理、基于顶点归并排序的并行宽度优先遍历、生成树验证、结果输出等。其中，与基于顶点排序的并行图遍历优化相关的流程步骤主要有：基于顶点度数的预处理、基于顶点重排序的并行宽度优先遍历优化。

基于顶点度数的预处理主要包括以下两个关键步骤：

步骤1 遍历图G=(V，E)中每个顶点，并记录每个顶点的度数，得到顶点度数集合D，D中第i个元素deg(vi)表示顶点vi的度数，即有deg(vi)个顶点与顶点vi之间存在相连边。

步骤2 采用归并排序算法，对D中的元素进行降序排序，得到排序后的顶点度数二元组集合D2如下：

D2=(〈v0，deg(v0)〉，〈v1，deg(v1)〉，…，〈vi，deg(vi)〉，…) ，

其中，D2中第i个元素〈vi，deg(vi)〉表示顶点vi的度数为deg(vi)且满足deg(v0)>deg(v1)>deg(vi)。将V中的顶点根据D2进行降序排序，得到排序后的顶点集合为(v0，v1，…，vi，…)，其中第1个元素v0对应顶点度数最大的顶点，第2个元素v1对应顶点度数仅小于或等于度数最大的顶点，度数相同的顶点并列重复列出。

基于顶点归并排序的宽度优先遍历算法的主要流程结构如图5所示。

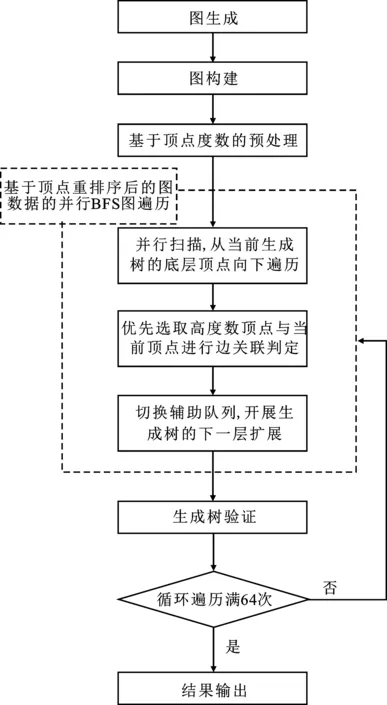
图5 基于顶点归并排序的BFS图遍历流程图

基于代码1的并行BFS伪代码，该策略在第9行的for eachvc∈Fcurparallel do后引入顶点度数 deg(vc)，先从高度数顶点vc开展遍历。考虑高度数顶点存在边关联概率高的特性，在代码1中第11行for eachvu∈G.Adj[vc]parallel do中，优先高度数顶点vu，判断其是否与vc相关联，是否可以加入生成树。

这一策略基于高度数顶点存在边关联概率高的特点。首先，引入了顶点度数deg(vc)。在遍历时，当累积存在deg(vc)个顶点vu与当前顶点vc存在边关联，可确定vc的关联顶点已全部遍历，会提前终止后续访存操作。其次，由于顶点vu度数高，与vc之间存在边关联的可能性也高，因此，该访存关联判定成功的概率较高，在提前终止后续访存操作前，较大限度地避免了盲目搜索情形的出现。最后，在自下向上宽度优先遍历算法阶段，鉴于高度数顶点的关联概率高、击中概率大的特点，更能高效查找并确定顶点vc的父顶点，继而终止顶点关联访存判断，以减少无效访存。

基于顶点排序的并行宽度优先遍历算法的具体实现伪代码见代码2，其算法描述如下：

(1)采用变量Fcur表示当前待搜索的顶点集合，Fnext表示下一层顶点搜索的顶点集合(即Fcur中顶点的所有邻接顶点)。

(2)开展检索之初，将根顶点vroot加入Fcur。

(3)引入当前顶点vc的度数deg(vc)。在遍历阶段，基于已经排序完成的顶点列表，按度数由高到低，取顶点vc的关联顶点vu进行访问。若顶点vu此前未被访问过，则更新其访问信息，并将该邻接顶点加入Fnext集合。

(4)如果当前顶点vc的已访问关联顶点vu的数目大于等于deg(vc)，则退出此次对vc关联顶点vu的循环遍历，在Fcur中取下一个顶点vc开展访问。

(5)每轮迭代结束时，将Fnext赋给Fcur并将Fnext清空，再循环执行迭代，直至待搜索顶点集合Fcur为空。

代码2基于顶点排序的并行宽度优先遍历算法的伪代码。

输入：G(V，E)，vroot。

输出：

①Fcur←ø

②Fnext←ø

③ for allvc∈V parallel do

④ visited[vc]=0

⑤ end for

⑥ visited[vroot]=1

⑦Fcur←vroot

⑧ whileFcur≠ø do

⑨ for eachvc∈Fcurparallel do

⑩ get deg(vc)

3.3 关键顶点优先缓存策略

关键顶点，即在图结构中与大部分顶点存在边关联的高度数顶点。优先缓存关键顶点，就是将部分高度数顶点缓存在天河系统区域内部的核组中的高速缓存中，对缓存的关键顶点进行优先访问。

对关键顶点进行优先缓存，既可以简化关联顶点之间的通信路径，减少顶点间的跨节点通信，又可同时提高顶点的访问命中率。但是，待缓存的关键顶点集合应结合机器特征和工程经验确定，需要考虑以下因素：

(1)高度数顶点应尽可能优先缓存；

(2)应结合节点内存效率考虑，在尽可能多地缓存高度顶点时，尽可能减小节点内存耗用量。

通过顶点排序统计分析，Kronecker图生成器生成的顶点度数分布中，度数大于1 000的顶点占比小于0.5%，度数大于100且小于1 000的顶点占比约5%，度数大于10且小于100的顶点占比大于20%。由于度数大于100的范围区间属于高度数顶点集中区域，占比合适，便于采用分布式共享存储模式缓存，因此，在VS-Graph500中，选择对度数大于100的顶点进行优先缓存。这样，一来能够缓存较高比例的高度数顶点，便于开展算法层面上的优化；二来每个节点分摊的内存大小也在可接受限度内，不会明显降低节点的内存效率。

4 实验与讨论

为了验证天河超级计算机系统的数据密集型应用处理能力，笔者提出了以顶点排序和优先缓存策略为基础的大规模图遍历优化方法，并将该方法应用于天河超级计算机系统的Graph500测试中，形成了面向天河超级计算机系统Graph500测试版本VS-Graph500。

4.1 实验配置

与Graph500测试密切相关的系统参数如表1所示。

表1 面向Graph500的系统配置

实验平台的功能结构组成如图6所示。该天河超级计算机系统实验平台按系统功能分为智能计算、存储、互连、服务、监控管理几大模块，总共包含8个机柜。每个柜包含2个互连交换插框，3个计算插框，1个存储插框。全系统包含768个计算节点(每个计算节点包含一颗众核处理器)，256个存储节点，1组高速互连网络，1组监控管理网络，1组基础架构。

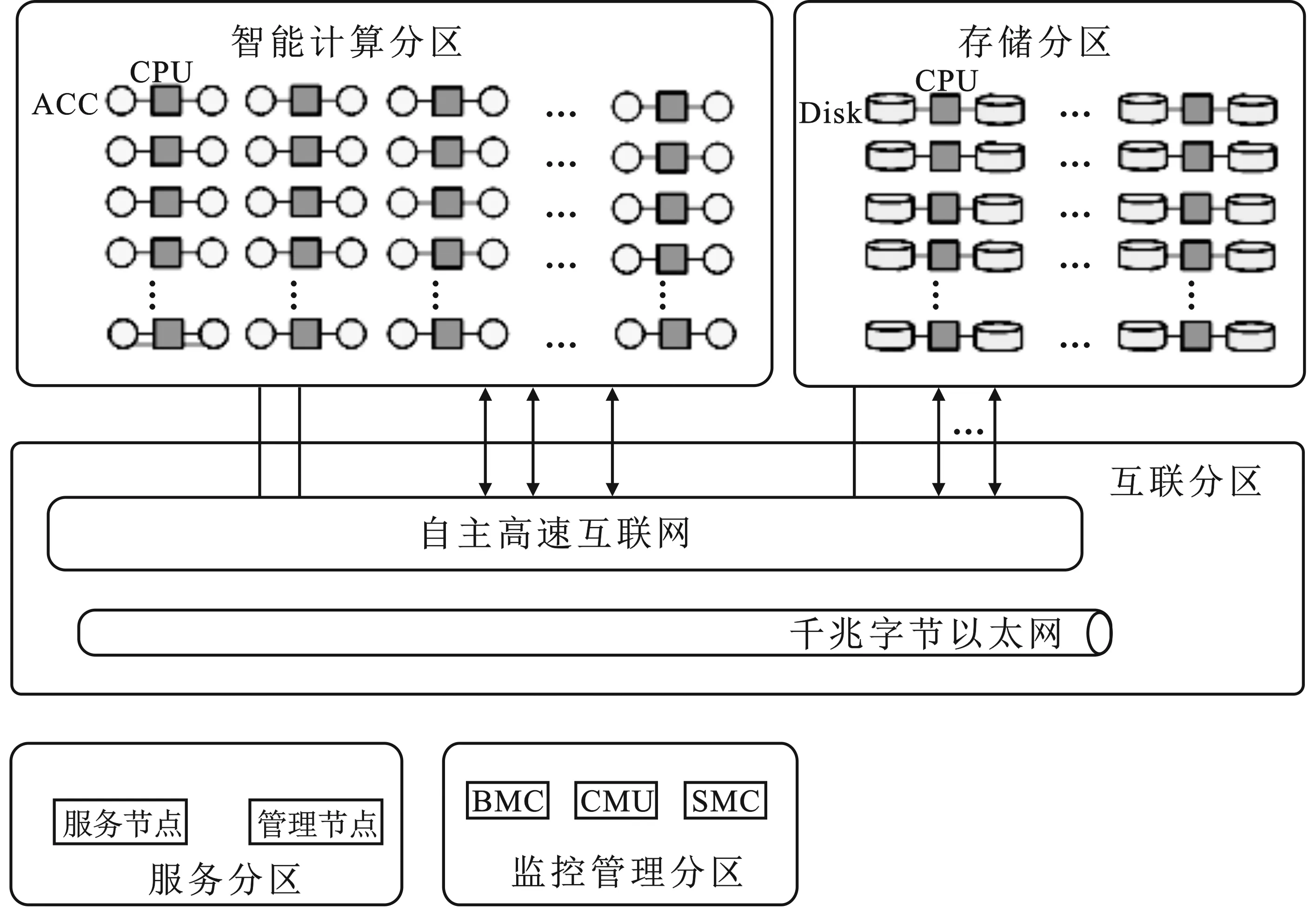
图6 VS-Graph500测试系统体系结构

该天河超级计算机系统实验平台的总节点数为1 024个，单节点核数为64，总核数为65 536个，单节点内存为128 GB，平台总内存为131 072 GB，带宽为200 Gbit/s，搭载麒麟系统及飞腾处理器。

为了验证以顶点排序和优先缓存策略为基础的大规模图遍历优化方法的有效性，对以顶点排序和优先缓存策略为基础的大规模图遍历方法优化后的VS-Graph500进行了详细测试，并选用Graph500官方基准测试程序、面向天河二号的Graph500程序TH-2A、面向“K”系统的Graph500测试程序，与VS-Graph500展开了对比分析。

4.2 基于顶点归并排序的大规模图遍历性能分析

排序算法是高性能计算机体系结构的经典算法，应用广泛。常用的排序算法有冒泡排序、快速排序和归并排序等。冒泡排序简单易实现，但时空复杂度较高；快速排序虽然空间复杂度较低，但时间复杂度较高；归并排序时空复杂度均较低，并且归并排序易于并行、易于向量化，能够很好地发挥国产飞腾众核处理器的计算性能。

面向天河超级计算机系统的Graph500测试版本VS-Graph500在天河二号平台上开展优化。为了准确地评估基于顶点归并排序方法对VS-Graph500的性能，程序中配置了各种独立的顶点排序优化模块，主要包括顶点度数排序、向量化排序优化以及孤立顶点剪枝优化等。详细评测性能如图7所示。

由图7可知，在加入顶点排序优化模块后的VS-Graph500程序中，图遍历性能提升显著，相比无排序时的Graph500基准测试程序的数据，其图遍历性能提升2倍以上。

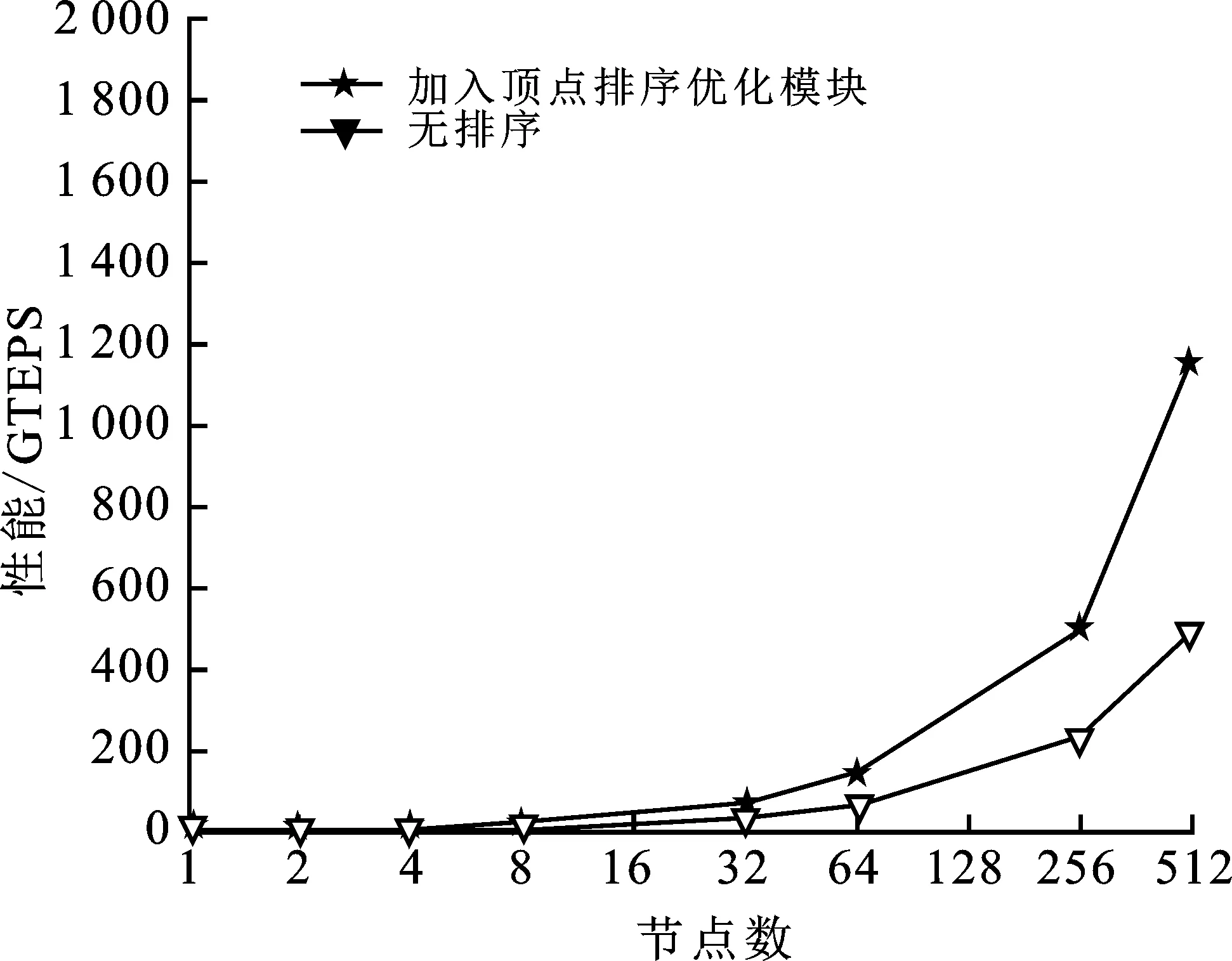
图7 顶点排序优化性能评测图

VS-Graph500程序中的顶点排序优化模块主要配置了归并排序(Merge Sorting)、快速排序(Quik Sorting)、冒泡排序(Bubble Sorting)以及无排序(without Sorting)等优化选项，应用各类排序算法后的VS-Graph500在天河超级计算机实验平台上的性能表现如图8所示。

图8 采用不同排序方法的顶点重排序阶段的耗时评估图

鉴于节点规模跨度大，小规模节点下可以支持的最高Fscale不能在大规模节点上有效展现各类排序方法带来的耗时差异，该参数不适宜确定为常量。因此，在不同节点规模下，本实验默认采用当前平台的最大可支持Fscale为参数，生成图并投入VS-Graph500程序中开展测试。因此，在图8中，随着节点规模的扩大，生成图Fscale增长，节点间的通信开销显著上升，使得顶点重排序阶段的耗时明显增加。

如图8所示，由于归并排序的时空复杂度均较低，易于并行化、向量化，能够更好地发挥国产飞腾众核处理器的性能，采用归并排序选项的VS-Graph500在顶点重排序阶段的时间开销明显优于采用快速排序和冒泡排序的版本，而配置快速排序的VS-Graph500略优于冒泡排序版本。

随着运行规模的增大，归并优化表现的性能优势越来越明显，同时其性能加速效果稳定，表现出良好的可扩展性。但是，当VS-Graph500在小规模节点上运行时，并未像在大规模节点上运行时一样表现出良好的性能优势。主要原因在于，当Fscale较小时，图数据的小世界性和无尺度性特征以及顶点度数分布的“长尾”现象表现得并不明显，且采用归并排序进行优化时的逻辑分支开销大。

详细的性能收益代价评估测试如图9所示。

图9 归并优化的代价收益评估图

在图9中，收益对应于引入归并排序优化后的VS-Graph500程序的图遍历性能，代价对应于未引入归并排序优化的标准Graph500程序的图遍历性能。实验数据以128个节点为界分为两组，当节点数<128时，纵轴的取值范围为0～200；当节点数≥128时，纵轴的取值范围为0～2 000；以便清晰呈现不同节点规模上的收益代价数据。

由图9可知，随着VS-Graph500运行规模的增大，在8节点时，归并优化代价收益比最大。这是因为图输入规模较小，图数据的小世界性和无尺度性特征以及顶点度数分布的“长尾”现象表现不明显。而随着测试规模的进一步增大，归并优化的代价收益比逐步减小并趋于稳定。在全系统测试时，归并优化的代价收益比突然增大，这是因为随着测试规模的增大，大规模图数据的特征越来越趋于真实数据集，“长尾”现象表现也越来越明显。当“长尾”现象趋于稳定后，节点间的归并通信开销成为关注点。

需要说明的是，为了简化分析，笔者将由顶点归并排序优化延伸的向量并行优化以及孤立点剪枝优化带来的性能提升，统一归集于顶点归并优化的性能提升。

综上所述，基于顶点归并排序的大规模图遍历算法，其性能表现优异，并具有良好的可扩展性。

4.3 关键顶点优先缓存性能分析

在不同图测试规模下的图顶点分布不同，而关键顶点在所有图顶点中的占比基本恒定在5%左右。关键顶点的优先缓存，是将排序后的高度数顶点缓存在天河系统核组内的高速缓存中，其缓存策略需要结合机器特征和工程经验确定。VS-Graph500主要选取度数大于等于100的图顶点组成关键顶点集合，在不同规模下配置关键顶点优先缓存策略后，其性能测试数据如图10所示。

图10 关键顶点优先缓存策略的性能评测图

由图10可知，在归并排序的基础上引入关键顶点排序后，VS-Graph500的测试性能进一步提升。与仅配置归并排序、无关键顶点优先缓存策略时的程序测试结果相比，优先缓存关键顶点后的VS-Graph500性能提升可达30%。这是因为，将关键顶点优先缓存至核组内的高速缓存后，大量的访问请求将发送至高速缓存内，与原先的普通存储模式相比，有效地提升了遍历阶段的访问效率。

同时，随着Graph500测试规模的增大，应用关键顶点优先缓存技术后的图遍历性能同步提升，表明该程序的可扩展性佳。

4.4 VS-Graph500性能分析

面向天河超级计算机智能应用场景，应用顶点排序和优先缓存优化定制的VS-Graph500全系统性能测试如图11所示，其展现的图遍历性能数据均基于对应节点规模下能够稳定测试的最大图规模。其中，面向“K”系统的Graph500在相关公开文献及相关资料的基础上集成开发，并不代表其实际能力。

图11 基于天河超级计算机的VS-Graph500性能测试

基于度数高的关键顶点与其他顶点关联概率高的特性，在顶点排序优化策略中，图中所有顶点按照度数高低从大到小进行重排序，便于提前中止冗余访存，最大可能地减少了不必要的访存和对外通信。而在关键顶点优先缓存策略中，图中各个顶点对缓存在buffer中的关键顶点进行优先访问，能够有效地提升图遍历时的访问效率。

由图11可知，面向天河超级计算机测试系统开发的 VS-Graph500 的性能与各个版本的Graph500测试程序相比，其性能提升显著。在全系统为1 024个节点、但有效可用节点数最多为904个，而图测试规模Fscale=37时，VS-Graph500的稳定测试性能为2 547.13 GTEPS，已超过2020年11月Graph500排行榜第7名的 2 061.48 GTEPS。同时，随着系统测试规模和图测试规模的增大，VS-Graph500程序的性能测试数据也随之增长，可扩展性好。

需要说明的是，904个节点上的VS-Graph500的测试性能并不能表明在数万节点甚至更大规模上VS-Graph500的性能表现能同比增长，因为系统规模越大，Graph500的性能影响因素会更多，因此更复杂。

5 总 结

大规模图处理是评测超级计算机系统处理数据密集型应用能力的重要手段。天河超级计算机系统将面向大科学、大工程计算，兼顾海量信息，大数据智能处理，拓宽应用领域。为此，面向天河超级计算机系统，利用大规模图数据的小世界性和无尺度性等特征，以及图数据顶点度数分布呈现的“长尾”现象，笔者提出了基于顶点归并排序和关键顶点优先缓存策略的大规模图遍历优化方法。应用优化程序VS-Graph500，在天河超级计算机系统实验平台上验证了上述优化方法的有效性和良好的可扩展性。在天河超级计算机系统实验平台全系统最多可用的904个节点上，VS-Graph500程序的实测性能为2 547.13 GTEPS，超过Graph500排行榜第7名。