非负矩阵分解的自适应单调投影Barzilai-Borwein算法

刘丹 黄亚魁

摘要 提出一种新的自适应单调投影Barzilai-Borwein（BB）算法求解非负矩阵分解（NMF）。算法不使用任何线搜索，并利用自适应BB步长和梯度的利普希茨常数加速算法收敛。在适当的条件下，证明了算法的全局收敛性。此外，将算法应用于稀疏对称非负矩阵分解，数值实验表明算法是有效的。

关 键 词 非负矩阵分解;交替最小二乘算法;自适应投影Barzilai-Borwein算法;稀疏对称非负矩阵分解

中图分类号 O29     文献标志码 A

文章编号：1007-2373（2021）06-0044-07

Abstract We present a new efficient adaptive monotone projected Barzilai-Borwein （BB） method for nonnegative matrix factorization （NMF）. Our method adaptively adopts the BB stepsizes without using any line search. The Lipschitz constant of gradient is exploited to accelerate convergence. Global convergence of the proposed method is established under mild conditions. Moreover， our method is applied to sparse symmetric NMF. Experimental results show that our method is promising.

Key words nonnegative matrix factorization; alternating nonnegative least squares; adaptive projected Barzilai-Borwein method; sparse symmetric nonnegative matrix factorization

首先，测试了随机生成的NMF问题。在MATLAB中使用rand函数随机生成[m×n]的矩阵[V]，对每个[V]和给定的r，随机生成10个不同的初始点[（W0，H0）]进行测试。表1给出了由这些初始点得到的平均结果，其中Iter表示求解问题（1）的迭代次数，Niter表示求解子問题（2）和（3）的总迭代次数，Nproj表示投影的计算次数，Time表示求解问题（1）花费的CPU时间，Pgn表示[[∇PHF（Wk，Hk），∇PWF（Wk，Hk）T]F]的最终值，Residual表示[V-WkHkFVF]的最终值。可以看出，对不同维数的矩阵[V]，AMPBB算法在迭代次数、子迭代次数、投影的计算次数方面优于其他3种算法，并且AMPBB算法花费的CPU时间最少。此外，4种算法得到Pgn和Residual的结果相差不大。

其次，测试CBCL和ORL人脸图像数据集。CBCL数据集包含2 429张人脸图像且每张图像的像素为19×19，该数据集可表示为1个361×2 429的矩阵。ORL数据集包含400张人脸图像且每张图像的像素为92×112，该数据集可表示成1个10 304×400的矩阵。表2给出4种算法使用10个随机产生的初始点对这2个矩阵分解的平均结果。显然，AMPBB算法投影的计算次数和CPU时间优于其他3种算法。

2.2 稀疏symNMF问题

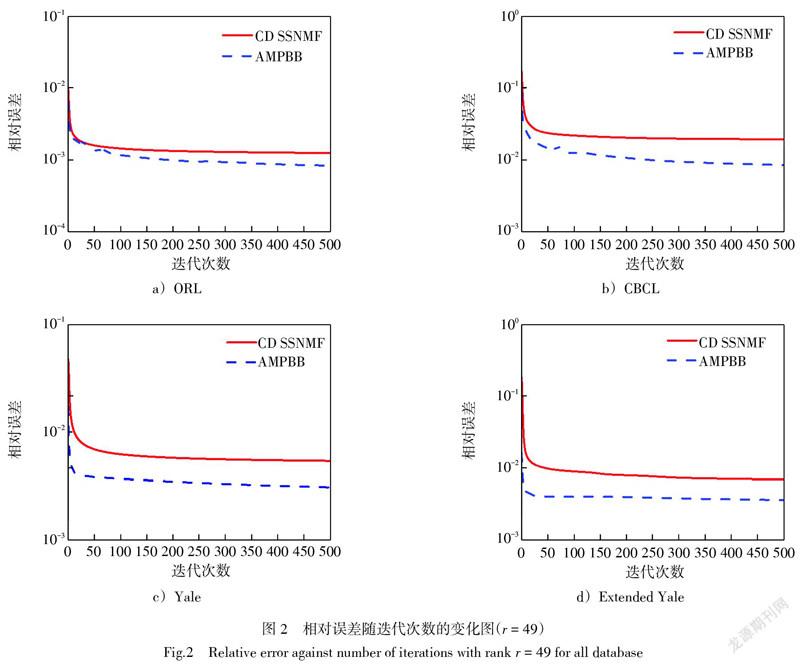
本节测试稀疏symNMF问题，将AMPBB与CDSSNMF[17]算法在数据集ORL、CBCL、Yale和Extended Yale上进行比较。ORL数据集包含400张人脸图像且每张图像的像素裁剪为32×32，该数据集可表示成1个1 024×400的矩阵;CBCL数据集表示成一个361×2 429的矩阵;Yale数据集包含165张人脸图像且每张图像的像素为32×32，该数据集可表示成一个1 024×165的矩阵;Extended Yale数据集包含2 429张人脸图像且每张图像的像素为32×32，该数据集可表示成一个1 024×2 429的矩阵。令矩阵C为数据集得到的矩阵，对称矩阵取[V=CCT]。参数选取[γ=5]和[λ=50]。为了公平起见，2种算法使用相同的终止条件，即最大迭代次数达到500次。图2描绘了AMPBB与CDSSNMF算法的相对误差随迭代次数的变化。可以看出，与CDSSNMF算法相比，AMPBB算法的相对误差更小。

3 结论

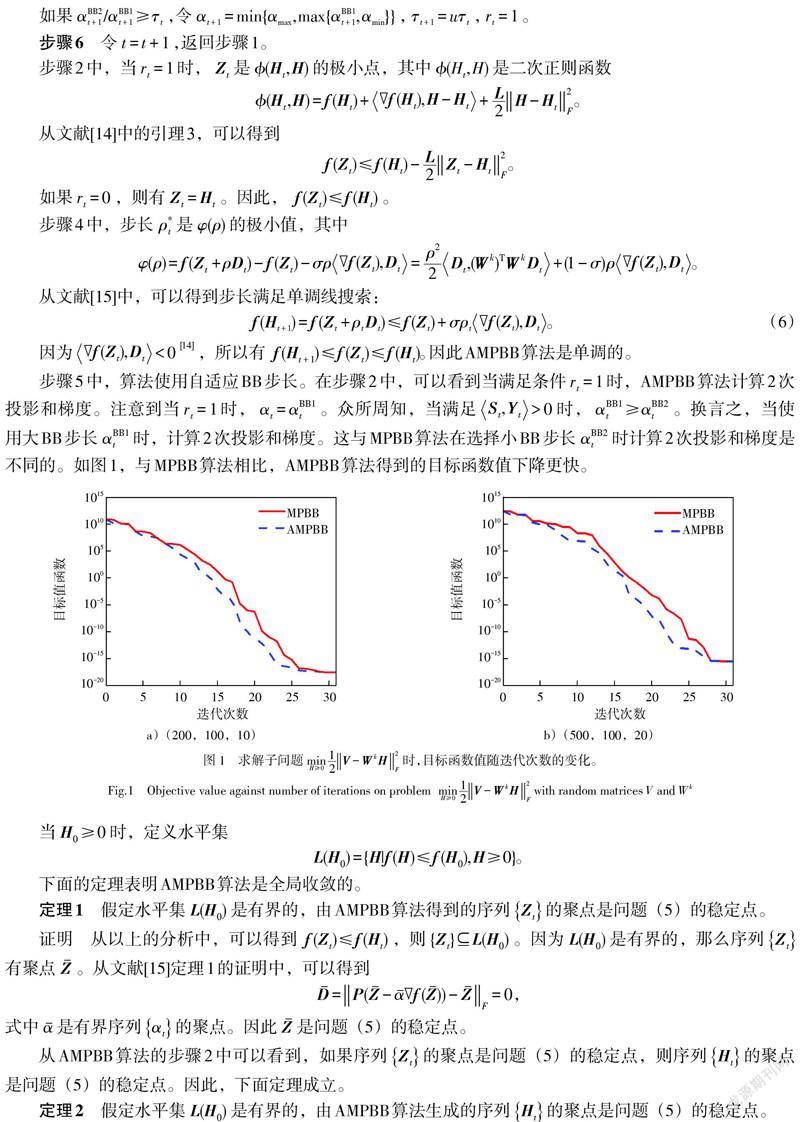
本文提出了一种新的自适应单调投影BB算法（AMPBB）求解非负矩阵分解（NMF）。AMPBB算法自适应地采用投影BB算法，当选取大步长[αBB1t]时，计算2次投影和梯度，这使得算法的目标函数值下降更快，投影的计算次数、迭代次数和消耗的CPU时间更少。此外，分析了算法的全局收敛性。数值实验表明，AMPBB算法是有效的。进一步，AMPBB算法应用于稀疏对称NMF，与CDSSNMF算法相比，AMPBB算法的相对误差更小。

参考文献：

[1]    LEE D D，SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature，1999，401（6755）：788-791.

[2]    STOEAN R，ATENCIARUIZ M A. Non-negative matrix factorization for medical imaging[C]// The European Symposium on Artificial Neural Networks，2018.

[3]    FU X，HUANG K J，SIDIROPOULOS N D，et al. Nonnegative matrix factorization for signal and data analytics：identifiability，algorithms，and applications[J]. IEEE Signal Processing Magazine，2019，36（2）：59-80.

[4]    BRUNET J P，TAMAYO P，GOLUB T R，et al. Metagenes and molecular pattern discovery using matrix factorization[J]. Proceedings of the National Academy of Sciences of the United States of America，2004，101（12）：4164-4169.

[5]    VAVASIS S A. On the complexity of nonnegative matrix factorization[J]. SIAM Journal on Optimization，2010，20（3）：1364-1377.

[6]    LEE D D，SEUNG H S. Algorithms for nonnegative matrix factorization[C]// Advances in Neural Information Processing Systems，2001，556-562.

[7]    BERRY M W，BROWNE M，LANGVILLE A N，et al. Algorithms and applications for approximate nonnegative matrix factorization[J]. Computational Statistics & Data Analysis，2007，52（1）：155-173.

[8]    PAATERO P，TAPPER U. Positive matrix factorization：a non-negative factor model with optimal utilization of error estimates of data values[J]. Environmetrics，1994，5（2）：111-126.

[9]    GRIPPO L，SCIANDRONE M. On the convergence of the block nonlinear Gauss-Seidel method under convex constraints[J]. Operations Research Letters，2000，26（3）：127-136.

[10]  LIN C J. Projected gradient methods for nonnegative matrix factorization[J]. Neural Computation，2007，19（10）：2756-2779.

[11]  GONG P H，ZHANG C S. Efficient nonnegative matrix factorization via projected Newton method[J]. Pattern Recognition，2012，45（9）：3557-3565.

[12]  HAN L X，NEUMANN M，PRASAD A U. Alternating projected Barzilai-Borwein methods for nonnegative matrix factorization[J]. Electronic Transactions on Numerical Analysis，2010，36：54-82.

[13]  GUAN N Y，TAO D C，LUO Z G，et al. NeNMF：an optimal gradient method for nonnegative matrix factorization[J]. IEEE Transactions on Signal Processing，2012，60（6）：2882-2898.

[14]  HUANG Y K，LIU H W，ZHOU S S. Quadratic regularization projected Barzilai-Borwein method for nonnegative matrix factorization[J]. Data Mining and Knowledge Discovery，2015，29（6）：1665-1684.

[15]  HUANG Y K，LIU H W，ZHOU S. An efficient monotone projected Barzilai-Borwein method for nonnegative matrix factorization[J]. Applied Mathematics Letters，2015，45：12-17.

[16]  ZHOU B，GAO L，DAI Y H. Gradient methods with adaptive step-sizes[J]. Computational Optimization and Applications，2006，35（1）：69-86.

[17]  BELACHEW M T. Efficient algorithm for sparse symmetric nonnegative matrix factorization[J]. Pattern Recognition Letters，2019，125：735-741.

[18]  KUANG D，YUN S，PARK H. SymNMF：nonnegative low-rank approximation of a similarity matrix for graph clustering[J]. Journal of Global Optimization，2015，62（3）：545-574.

[19]  HE Z S，XIE S L，ZDUNEK R，et al. Symmetric nonnegative matrix factorization：algorithms and applications to probabilistic clustering[J]. IEEE Transactions on Neural Networks，2011，22（12）：2117-2131.

[20]  LANG L Y，JING X K. Application of Non-negative sparse matrix factorization in occluded face recognition[J]. Journal of Computers，2011，6（12）：2675-2679.

[21]  DOBROVOLSKYI H，KEBERLE N，TERNOVYY Y. Sparse symmetric nonnegative matrix factorization applied to face recognition[C]//2017 9th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems：Technology and Applications （IDAACS）. September 21-23，2017，Bucharest，Romania. IEEE，2017：1042-1045.