基于ITD和排列熵的行星齿轮箱故障诊断方法
2021-02-18胡爱军朱丽佳
胡爱军,朱丽佳,向 玲
(华北电力大学能源动力与机械工程学院,河北 保定 071003)
行星齿轮箱广泛应用于风力发电机等设备,与固定轴齿轮箱相比,行星齿轮箱结构紧凑、传动比大,适用于输出功率要求较高的机械[1]。风力发电机齿轮箱发生故障会带来巨额维修费用[2],准确诊断行星齿轮箱的故障具有重要的应用价值。由于行星齿轮箱常常在低速重载的环境下工作,故障诊断难点体现在故障响应微弱、振动信号不平稳、特征频率复杂等方面[3]。
近些年,国内外学者对行星齿轮箱的诊断开展了广泛研究。McFadden 等[4]对行星齿轮箱进行研究,建立模型解释振动谱在啮合频率存在调制侧带的不对称性,甚至完全抑制了成分的原因。冯志鹏等[5]根据行星齿轮箱振动信号的调频特点,提出了基于经验模式分解的频率解调分析方法,以及本质模式函数的选择原则,推导出太阳轮、行星轮的瞬时频率傅里叶频谱结构特点。丁闯等[6]利用排列熵(Permutation Entropy,PE)的优点,实现了行星齿轮箱正常和裂纹故障2 种状态的区分。在此基础上,丁闯等[7]又提出一种结合局部均值分解(Local Mean Decomposition,LMD)和PE 的方法。先将信号进行LMD 分解,然后针对包含有故障信息的分量进行PE 计算,以此诊断故障。冯志鹏等[8]利用固有时间尺度分解(Intrinsic Time-scale Decomposition,ITD)优点,提出了一种幅频联合解调分析方法,将信号进行ITD 分解,对敏感分量的瞬时振幅和瞬时频率进行傅里叶变换,有效地提取故障频率。
行星齿轮箱故障信号成分复杂,易受噪声影响。仿真和实验分析表明,分析效果受数据选择的影响。利用ITD 算法提取故障特征能力强[9]的优点对信号分解,分解后根据互相关系数选取敏感分量,再用抗噪声能力强[10-11]的PE 计算熵值,最后依据最小熵原则选取数据,进行包络分析。研究表明,ITD-PE 方法可以有效增强故障特征,准确诊断故障。同时,根据故障的不同程度熵值存在差异,能够实现故障程度的区分。
1 ITD-PE分析方法
1.1 ITD基本原理
行星齿轮箱故障信号复杂,选用对复杂信号分解适应性强[8]的ITD 分解信号,降噪效果较好。ITD 能将信号分解成旋转分量(Proper Rotation,PR)和单调趋势分量之和[12]。算法过程如下:先假设原始信号Xt的极值为Xk,对应时间为τk(k=1,2,…,M),M为所有极值点个数;再定义信号分段线性基线提取算子Lt为
式中:0 <α<1,一般取α=0.5。
定义固有PR提取算子为

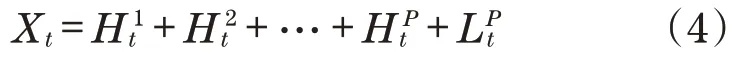
1.2 PE基本原理
PE 由 Christoph 等[13]首次提出,是衡量一维时间序列复杂度的参数,PE 值越小,说明时间序列越稳定[6]。方法大致步骤是先对时间序列进行相空间重构,得重构矩阵Y:
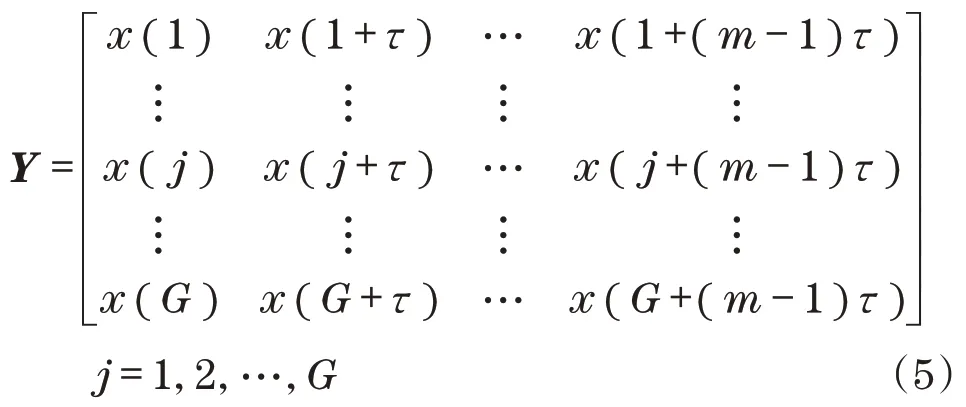
式中:m为嵌入维数;τ为延迟时间;G为重构向量个数。
接着,对Y中的第j个重构分量升序排列,若存在元素相等则按原顺序排。所以,重构向量X(j)经排列后得到一反映元素大小顺序的S(l)=[j1,j2,…,jm],其中,l=1,2,…,g。每一种符号序列出现的概率为Pk,然后计算符号序列X(i)的k种不同符号序列的PE可定义为
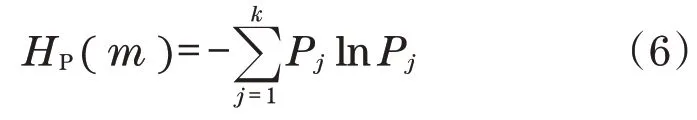
对HP(m)标准化,即,HP的取值范围为 0 ≤HP≤ 1。
研究表明,PE 对行星齿轮箱信号敏感,若行星齿轮箱存在故障将产生冲击,比正常状态更规律,熵值降低[7]。利用PE 大小可实现行星齿轮箱的故障区分。
1.3 ITD和PE实现过程
首先,将原始信号分成长度相等的多个子序列,各子序列经ITD 分解得到若干PR。其次,利用互相关系数准则,筛选出与原始信号相关系数最大的 PR 分量[12],作为敏感分量,对敏感分量求PE。最后,依据最小熵原则选取数据段,进行包络分析。本文从仿真和实验两方面验证了ITDPE 既能实现故障的有效诊断,也能利用熵值不同进行故障程度的区分。ITD-PE 实现过程的流程如图1 所示。
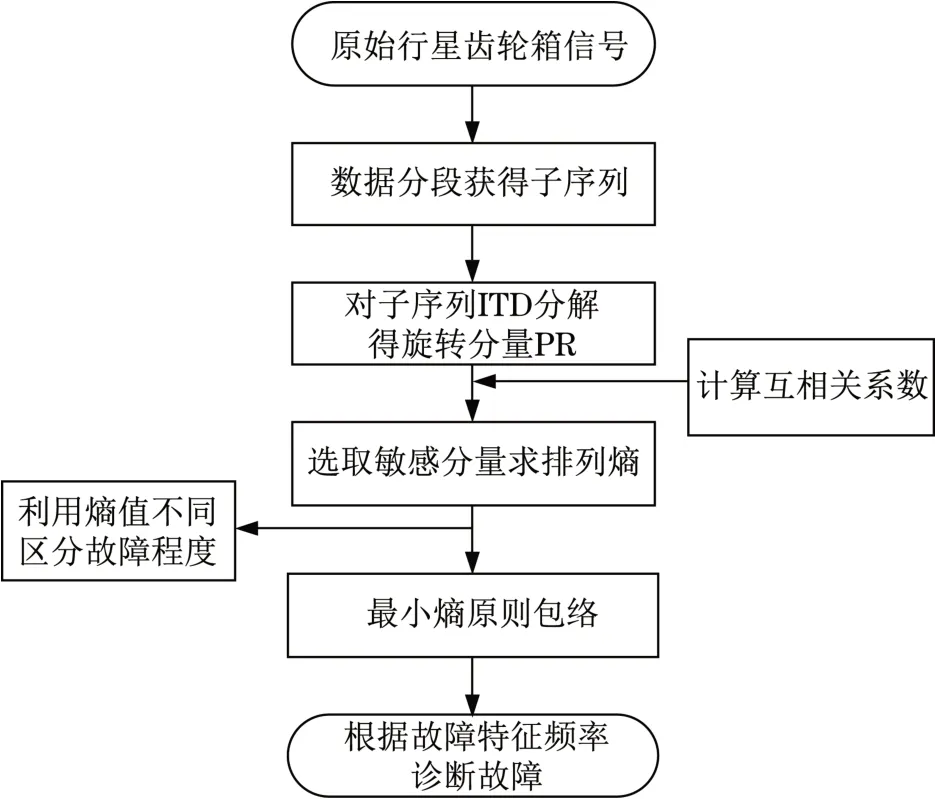
图1 ITD-PE流程图Fig.1 The flow chart of ITD-PE
2 仿真信号分析
结合文献[6]中行星齿轮箱太阳轮局部故障信号的特点,以信号幅值大小表征故障程度,仿真了4种太阳轮信号。其中,仿真信号1为正常状态,仿真信号2~4为不同程度的故障状态,其表达式如下。

其中,行星齿轮箱太阳轮驱动端的输入转速n=2 400 r/min,太阳轮齿数Zs=20,行星轮齿数Zp=40,内齿圈齿数Zr=100,行星轮个数Np=3,故障频率依据文献[14]具体计算过程如下:

假设仿真信号初相位都为0,幅值A=B=1,采样频率为5 120 Hz,为模拟噪声干扰,向仿真信号中加入-3 dB 高斯白噪声。4 种仿真信号数据长度为81 920,取子序列长度N=8 192,每个信号共10段。对每段子序列求PE,结果如图2所示。图中可见,信号2~4 的熵值都比正常信号1 的熵值低,说明信号2~4存在故障,与仿真情况相符。进一步观察图2 可知,同一仿真信号不同数据段的熵值大小有波动,且仿真2和4存在部分熵值交叉,不能完全区分的现象。选取任意信号的一组数据,如信号4的第10 组数据,经ITD 分解后时域图如图3 所示,PR分量与原信号互相关系数如表1所示,因第一个PR 分量相关系数最大,所以选作敏感分量并求PE。其他信号也运用ITD-PE 方法后如图4 所示,相比图2、图4 中信号2~4 的熵值能完全区分开。ITD-PE 方法与PE 对比,在区别正常、故障信号的基础上,还实现了故障不同程度的区分。

表1 X4(t)第10组数据互相关系数Tab.1 X4(t)the tenth set of data correlation numbers
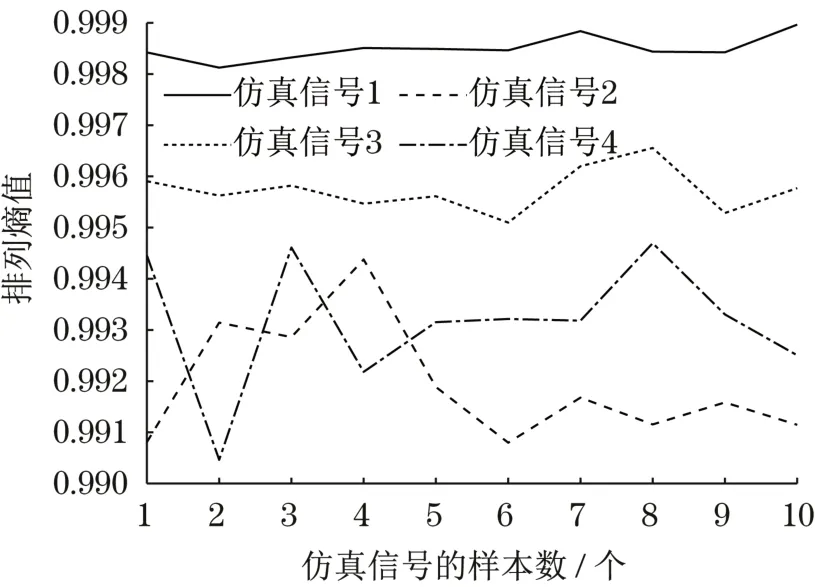
图2 仿真信号PEFig.2 Simulation signal PE
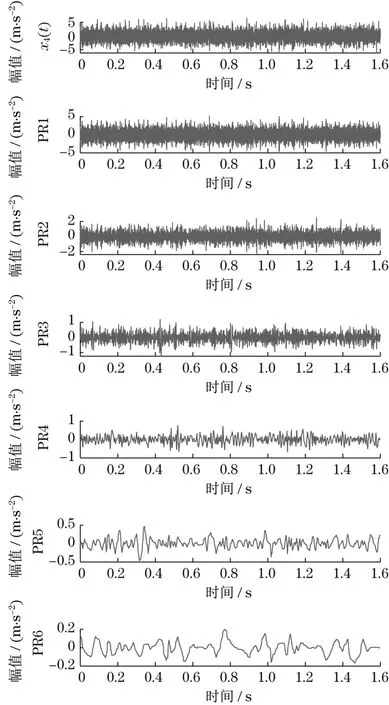
图3 X4(t)第10组数据ITD分解时域Fig.3 X4(t)the tenth set of data ITD decomposing the time domain
在区分故障程度的基础上,为了进一步诊断行星齿轮箱故障部位,现对任一故障信号进行分析。因图4中观察到同一信号各子序列熵值存在差异,在仿真信号4中选取熵值最小(第1组数据)和最大(第10组数据)2组数据包络分析,结果如图5所示。
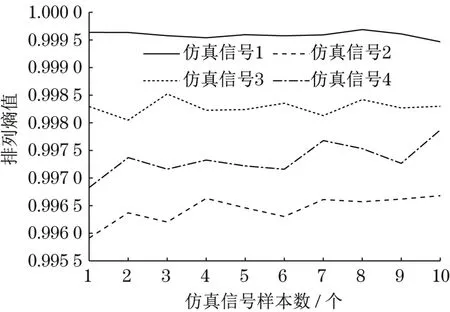
图4 仿真信号ITD-PEFig.4 Simulation signal ITD-PE

图5 仿真信号4敏感分量包络Fig.5 Simulation signal 4 sensitive component envelope
3 实验信号分析
为了进一步验证所提方法对实际行星齿轮箱故障信号的处理效果,用实验室测得的故障实验数据进行验证。实验台如图6 所示,行星齿轮箱的型号为ZLS160。其结构为齿圈固定,太阳轮轴作为输入,行星架为输出轴。行星齿轮箱参数为太阳轮齿数Zs=21,行星轮齿数Zp=31,内齿圈齿数Zr=84,行星轮个数Np=3。通过式(11)~式(14)计算得到在太阳轮上模拟点蚀、裂纹、断齿和缺齿4 种故障,如图7 所示。太阳轮轴转速为3 000 r/min,以采样频率20 480 Hz记录正常状态及太阳轮点蚀、裂纹、断齿和缺齿4种故障条件下的加速度传感器数据。

图6 行星齿轮箱实验台Fig.6 Experimental table of planetary gear box

图7 太阳轮4种故障Fig.7 Sun wheel four faults
对实验采集的4 种故障数据进行包络分析,可以诊断出点蚀、裂纹、断齿3 种故障属于太阳轮局部故障。但缺齿故障诊断效果不好,包络分析结果如图8 所示,图8 能找到而故障频率不突出。对于缺齿故障,需进一步寻找方法诊断故障。同时因太阳轮4 种故障特征频率相同,无法区分故障程度,也需继续分析。

图8 缺齿故障包络图Fig.8 Fault envelope diagram
5 种实验数据长度为196 608,取子序列长度N=32 768,每个信号共6 段。对每段子序列求PE,结果如图9 所示。与仿真分析结果(见图2)类似,图9 中太阳轮4 种故障都低于正常熵值,同一故障信号各数据段熵值大小不同,断齿与缺齿故障熵值存在混叠无法区分。按照图1 的流程,选取任意信号的一组数据,如缺齿第1 组数据经ITD 分解后时域图如图10 所示,PR 分量与原信号互相关系数如表2 所示,选分量PR1 作为敏感分量求PE。实验数据运用ITD-PE 方法处理后,结果如图11 所示,太阳轮4 种故障熵值明显不同,断齿、缺齿2 种故障得到区分。实验分析表明,ITD-PE 既能识别正常、故障状态,也能将故障频率相同的不同故障区分。

图11 实验数据ITD-PEFig.11 Experimental data ITD-PE

表2 缺齿第1组数据互相关系数Tab.2 The first set of data is the number of correlation between missing teeth

图9 实验数据PEFig.9 Experimental data PE

图10 缺齿第1组数据ITD分解时域Fig.10 The first set of missing teeth data ITD time domain decomposition
ITD-PE 方法对实验数据的分析实现了故障程度区分,但还需诊断行星齿轮箱故障部位。对缺齿故障熵值最小(第5 组数据)和熵值最大(第2 组数据)2 组数据包络分析,结果如图12 所示。图12(a)、图12(b)都能找到可诊断为太阳轮局部故障。继续比较发现,图 12(b)中能找到而图12(a)中被噪声淹没无法找到,且图12(b)中故障频率fs比图12(a)更明显。实验数据分析结果说明,依据最小熵原则选择数据段,可以较好实现故障诊断。与图8 对比,图12(b)中太阳轮故障频率fs突出,诊断为太阳轮局部故障的依据可靠。通过实验数据的验证,发现ITD-PE 方法对行星齿轮箱的故障诊断和故障程度区分有明显效果。

图12 缺齿故障敏感分量包络Fig.12 Sensitive component envelopment of missing tooth fault
4 结语
考虑到行星齿轮箱故障诊断困难,充分结合ITD 和PE 算法的优点,提出了ITD-PE 的行星齿轮箱故障诊断方法;运用互相关系数准则剔除伪分量,筛选敏感分量,提出了最小熵原则,为数据段选择提供了依据,使ITD 分解故障信号后的包络分析,能准确提取故障特征频率;给出了当故障特征频率相同时,可根据熵值大小区分故障程度的依据。本文从仿真和实验两方面,验证了所提方法在实现行星齿轮箱故障诊断的同时也可以区分故障程度。
