考虑初始变形的钢管脚手架稳定性分析*

赵元一，徐 佳，赵成成

(1.同济大学浙江学院，浙江 嘉兴 314051；2.浙江上嘉建设有限公司，浙江 嘉兴 314001)

0 引言

立杆是外脚手架应用的主要受力构件，在轴向压力作用下，立杆的变形及弯曲是控制架体稳定性的主要因素。以材料力学中的轴向铰接受力构件为基础，结合杆件的应变能及变分极值条件，综合考虑杆件侧向挠度、轴向变形等因素，能求解出基于多项式级数表达的压杆稳定临近荷载。童根树等通过理论和非线性计算软件，分析了预应力在压杆稳定性中的应用，但缺少杆件初始变形对压杆稳定性的分析。唐柏鉴等根据压杆的基本屈曲模态，通过典型的算例研究了模拟曲线项数对临界压力的预估精度，但未能明确初始变形与钢管压杆屈曲荷载的定量关系。

本文充分考虑钢管构件计算的复杂性，将精度与多项式级数相关联，并考虑杆件初始变形的影响，能充分得出构件出厂变形和杆件稳定性的估算值并确保计算的可靠性。

1 最小势能原理在简支杆件的应用

杆件一端铰接，另一端为可水平移动的杆件连接，在轴向压力作用下，杆件在轴向变形和挠曲变形方向均有一定变化，其计算模型如图1所示。

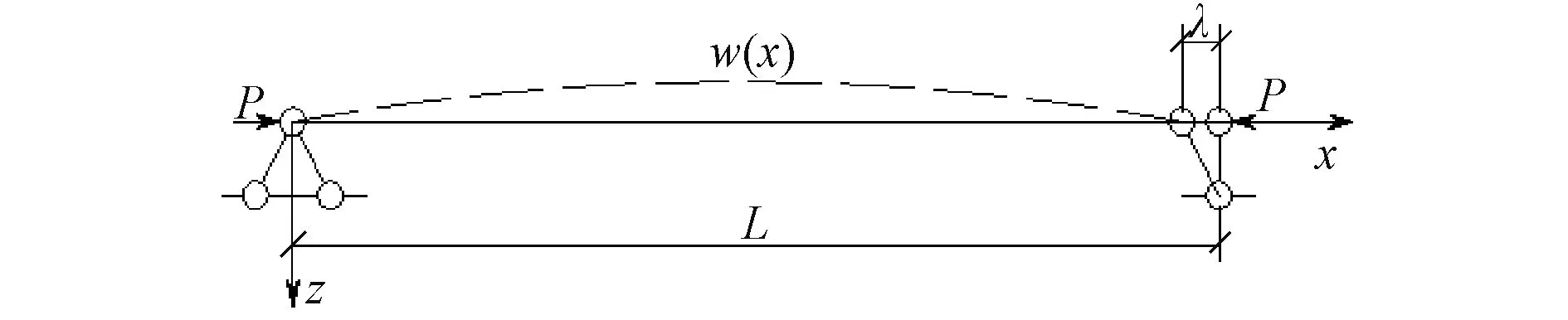
图1 轴向压力下杆件的计算模型

模型的抗弯刚度为EI，杆件总长度为L，杆件在x轴向的压缩量为λ。

1.1 杆件变形能极值条件的推导

受压杆件的应变能Π为：

(1)

式中：E为杆件材料的弹性模量；I为截面惯性矩；w为杆件挠度。

含有高阶导数的变分Euler方程为：

(2)

将杆件轴线位移的杆件应变能带入得：

受压杆件的Euler方程为：

(3)

式(3)即为杆件受弯的Euler-Poisson方程。

1.2 杆件边界条件的推导

假设杆件的整体变分为：

I[y(·)]=Φ(α)=

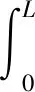
(4)

式中：W为所求杆件应变所对应的杆件轴线位移(杆件变形能极值所对应的轴线位移)；η为极值位移周边的任意小函数变化；α为常数。

要保证杆件整体变分在α=0处取极值，即Φ′(α=0)=0，将式(4)带入可得：

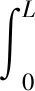
(5)

式中：右侧第2项经一次分部积分可得：

(6)

第3项经2次分部积分可得：

(7)

对于压杆而言，两端固定，其边界条件w(0)=w(L)=0，其边界转角和弯矩待定，由此可得压杆的边界条件为：

(8)

考虑到杆件的初始变形等因素，式(8)边界条件可适当放宽。综合可得杆件的整体Euler方程和边界条件为：

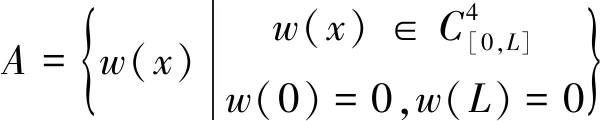
对杆件的弯曲采用勒让德(Legendre)多项式代替，即

(9)

考虑到在节点位置杆件的挠度为0及Euler方程的控制条件，则杆件的挠度曲线可化简为：

(10)

按常规多项式进行位移求解，考虑到在节点位置杆件的挠度为0和Euler方程的控制条件，则杆件的挠度曲线可化简为：

(11)

1.3 杆件外力做功

(12)

由此可得轴向压力做功为：

(13)

对于压杆结构，外力做功与结构应变能相等，即

(14)

将w和相应的表达式带入可得：

(15)

(16)

将式(15)～式(16)分别对C1，C2求偏导，化为矩阵形式为：

(17)

由此可求得待定系数P与杆件材料及几何尺寸的关系，此即为压杆对应的临界压力。

1.4 计算结果对比分析

对于多项式级数的位移，主要的位移分量为：

w(x)=C1x(x-L)

(18)

总体势能方程为：

(19)

与其相对应的杆件的轴向压力为：

(20)

由式(20)可看出，杆件在轴力作用下的临界压力值与材料力学中的解析表达式相近，其材料力学解析解为：

(21)

2 基于杆件变形能的挠度分析

由材料力学的压杆稳定方程可知，若无初始变形，杆件的挠度方程为：

(22)

(23)

由此可得方程的特解为：

(24)

式中：Cr为初始变形状态杆件的挠度幅值，由现场测量统计得出。

压杆稳定的临界压力Pcr普遍小于杆件的材料屈服强度，主要是因为在挠度作用下产生弯矩，引发杆件失稳。考虑到杆件的初始变形后，将材料力学的压杆稳定临界荷载式(21)代入式(22)，得出修正后的挠度曲线方程，并以此作为附加弯矩的修正项，结合材料的屈服强度对临界压力进行进一步修正，则有：

(25)

3 工程实例计算分析

施工规范中的主受力杆件(立杆)以直径48mm、壁厚3.5mm钢管构件作为主要应用构件，之后考虑到生产和现场应用的实际问题，将壁厚3.0mm的杆件也列入受力构件的计算范畴。考虑到现场应用较多的钢管型材，脚手架采用直径48mm、壁厚为3.0mm的钢管，材料屈服强度fy=205N/mm2，在施工过程中连墙件为两步两跨，底层脚手架考虑施工高度，其步距为1.80m，钢管在其步距内的初始变形幅值(50mm)下，其工作条件下的临界荷载Pcr的确定步骤如下。

1)假设在不考虑钢管初始变形的情况下，杆件的临界荷载。

2)考虑初始位移后的压杆挠度曲线，并求出挠度幅值A0。

3)确定考虑初始变形后的杆件挠曲线幅值后，进行修正后的弯矩求解。

由此可得修正后的杆件临界压力Pcr=2.62kN，远远小于杆件的理论临界荷载，初始变形对杆件的临界压力有较显著影响，控制初始变形能有效提高脚手架体系的承载力。因此，可得出脚手架立杆初始变形与其临界荷载的关系曲线，如图2所示。

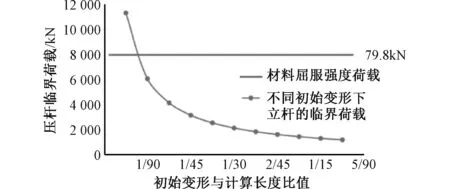
图2 初始变形影响下立杆的临界荷载

由图2可知，随着初始挠度的增加，脚手架立杆的受压临界荷载逐渐降低。当初始挠度与杆件计算长度之比为0～1/150时，其压杆临界荷载高于杆件的材料屈服强度，应以材料屈服强度为控制因素，取材料屈服强度为79.8kN；当初始挠度与杆长之比逐渐加大后，受压临界荷载下降较明显，当初始挠度幅值与杆件计算长度之比为1/45时，其临界荷载下降至材料强度的40%，之后随着杆件初始变形幅值的增大，压杆临界荷载下降趋于缓和。为确保立杆的稳定性，其初始挠度幅值应控制在一定幅度内，以防止杆件失稳。

为确保理论计算的可靠性，采用有限元计算软件MIDAS对压杆稳定性进行受力分析，考虑到压杆在轴力和初始变形下的挠度叠加，采用梁单元模型，对不同初始变形的压杆进行竖向受力分析，立杆长度为1.8m，用4个梁单元进行等效，其极限状态受力与理论计算结果对比如图3所示。

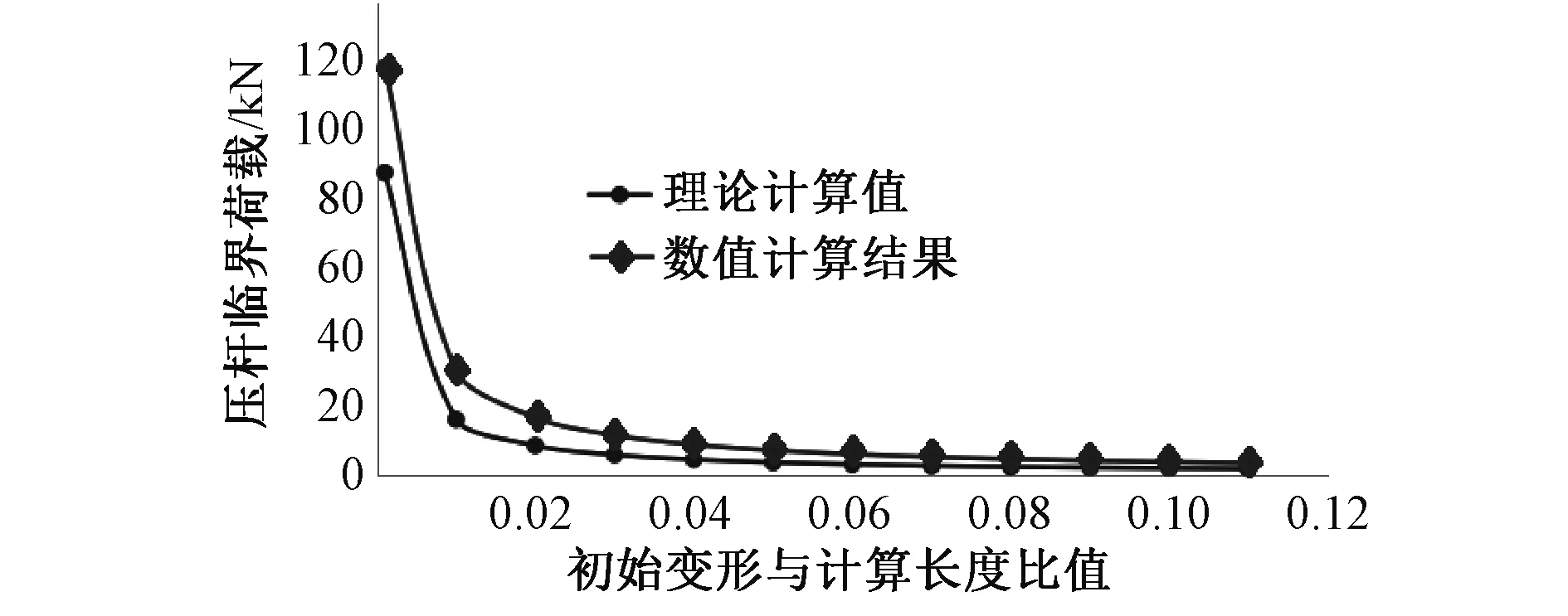
图3 立杆临界荷载的理论解与数值解对比

与有限元计算结果对比可得，其理论解整体结果与数值解基本一致，变化趋势也基本相同，由于数值解计算模型采用4个梁单元模拟，其变形刚度较实际情况大，所以数值解的极限稳定荷载比理论值稍显偏大。

4 结语

以杆件最小势能原理为基础，通过变分法和欧拉方程，计算分析了在轴向压力荷载作用下，压杆的临界稳定荷载解析及半解析解，将杆件初始变形代入压杆挠曲微分方程，计算并分析了初始变形对临界稳定荷载的影响，结论如下。

1)在轴向荷载作用下，压杆变形可通过结构变分和对应的欧拉方程求导得出，以麦克劳林展开式为基础的半解析方法通过多项式解进行拟合同样能得出较接近实际的结果，且计算量较小。

2)在考虑边界约束条件后的杆件初始变形后，其压杆的临界稳定荷载仍以材料屈服强度为界定条件，判断依据为杆件最大正应力不得超过材料自身的屈服强度。

3)初始变形对压杆稳定的影响较显著，以工程普遍采用的扣件式脚手架立杆为研究对象，不同的杆件初始挠度对杆件的附加弯矩和后续侧向变形影响较显著，与其对应的临界稳定荷载也随初始的侧向变形明显降低。