航空发动机叶片机器人砂带磨削的倾斜进给方法

任洪樟，黎 静，谢 乐

(1.重庆理工大学 机械工程学院，重庆 400054；2.重庆妙奇丰科技有限公司 技术部，重庆 400054)

砂带磨削作为涡轮叶片、螺旋桨叶等复杂曲面零件的一项关键精加工工艺，主要用于提高零件的表面光洁度和精度。工业生产中叶片打磨主要采用两种方法，一种是机床砂带磨削；另一种是机器人砂带磨削(它采用标准工业机器人和砂带磨削加载装置)。与适合大规模生产的传统机床砂带磨削方法相比，机器人砂带磨削方法具有更大的灵活性，已成为当今的主流应用。

控制材料去除率(MRR)是砂带磨削的关键，许多学者对其进行了研究。He等研究了不同接触压力对钢轨材料砂带磨削性能的影响，得出了加大接触压力对MRR有积极影响的结论[1]。Xiao等提出一种新的带式高效精加工方法，并建立了寿命周期材料去除模型[2]。利用该模型可以预测钛合金材料高效精密加工过程的材料去除寿命周期。Wang等提出一种偏离MRR非线性模型的复杂叶片表面的磨削去除轮廓模型[3]。Ren等提出一种机器人砂带磨削中材料去除率的局部化加工模型，并将其应用在了对砂带磨削过程的仿真[4]。Wang等在考虑接触轮弹性变形和工件特性的情况下，提出一种可控的材料去除策略，以提高加工效率和精度[5]。Wang等为准确预测切割深度，分析了皮带张力引起的接触轮变形，基于幂级数法和弹性力学理论建立了接触轮的张力模型[6]。实验表明，在给定的磨削方式下，其预测误差小于3.1%。为了研究砂带磨削过程中力的分布，Luo等提出一种显微尺度的犁削力模型， 并从能量角度对机器人辅助钛合金砂带磨削的切削机理进行了表征[7]。Zhang等提出一种基于支持向量回归(SVR)技术的计算力分布的有效模型[8]。与有限元模型相比，该模型的误差更小，计算速度更高。Weinert等提出的支持向量机(SVM)方法，可用来计算砂带磨削过程中力的分布[9]。Pandiyan等开发了一种多传感器集成技术，用于预测加工过程的表面粗糙度变化情况[10]。在有关表面质量的研究方面，Mezghani等研究了柔性涂层砂带上固定颗粒的主要特征与磨削性能之间的关系，以及用于精密砂带磨削的涂层磨料的评估方法[11]。为了提高整体叶盘在热环境下的静态和动态疲劳寿命，Xiao等提出一种基于抗疲劳制造原理的加工方法，其实验结果表明，用该方法加工的表面粗糙度小于0.4 μm[12]。有研究者在观察砂带刀具加工过程中磨粒退化的演变规律后，开发了基于SVM和遗传算法(GA)的砂带磨损在线检测预测分类模型[13]。为了改进砂带磨削工艺，许多学者还进行了优化进给的研究。Song等提出一种基于统计机器学习的自适应磨削模型，以平滑机器人控制的轨迹，缩短过渡过程的响应时间[14]。为了保持恒定的接触力，进而获得光滑的加工表面，Sun等提出一种新的机器人砂带磨削方法，通过系统校准和力的控制来提高磨削性能[15]。Wang等通过运动学分析，提出了一种有效的六轴数控砂带磨削机床的优化策略[16]。Hou等基于二阶密切原理，提出一种有效的平面磨削方法[17]。该方法能结合砂带磨削的特点，在磨削点调整接触轮的姿态，从而确定最佳的进给方向，减小磨削误差。为了提高复杂曲面工件的机器人砂带磨削系统的磨削质量，Gao等在引入灵巧磨削点和灵巧磨削空间新概念的同时，分析了影响灵巧磨削空间的因素[18]。

大量应用研究表明，砂带磨削过程对接触载荷非常敏感。这意味着，如果叶片坯料的表面残余量不均匀，要通过砂带磨削获得高精度表面的叶片，就必须对磨削过程的接触载荷进行动态控制。然而，如果在机器人砂带磨削中，机器人系统和负载系统不关联，夹持在机器人上的叶片坯料和砂带磨削装置上砂带轮之间接触载荷的控制，就很难通过不同型号机器人系统和负载系统的协同控制来实现。为此，本文提出一种倾斜进给的砂带磨削方法——通过改变砂带轮的倾斜方向来动态改变叶片和砂带轮的法向接触力。应用这种方法，使负载系统施加在砂带轮上的力能在加工过程中保持恒定，从而不再依赖于机器人系统和负载系统的协同控制。

1 浮动压力磨削装置

由于叶片的截面形线为高阶抛物线，其曲面结构复杂，加工残余量分布不均匀，因此对叶片表面的磨削，要求调节磨削机构施加压力的频率很高，对于砂带轮施加的接触力的响应要求也较高。但是，在实际磨削过程中，如果砂带轮施加的载荷过大，就会严重影响机床的结构稳定性及磨削效果。因此，在砂带磨削加工中，为防止砂带轮与被加工件之间的接触压力过大而出现的过磨烧伤现象，常通过浮动压力磨削装置来实时调节磨削压力。本文以丝杆、钢丝、弹簧、导杆等构成的主轴组件作为补偿机器人定位误差的调节机构，并选用伺服电机来控制弹簧的压缩量，实现对磨削压力的控制。

图1所示的浮动压力磨削装置主要由立柱、惰轮、张紧轮、砂带、驱动轮、驱动电机、伺服电机、气缸、主轴组件、压力传感器、导向轮等部件组成。

1.立柱；2，3.惰轮；4.张紧轮；5.砂带；6.驱动轮；7.驱动电机；8.伺服电机；9.气缸；10.主轴组件；11.压力传感器；12.导向轮；13.接触轮；14.丝杆;15.钢丝;16.弹簧;17.导杆图1 浮动压力磨削装置

与刚性砂轮磨削过程不同，砂带磨削是柔性的。在砂带磨削过程中，砂带与工件表面的接触为弹性接触。随着机器人的运动，工件沿其表面的切线方向进给。但是，由于弹簧提供的接触力一直存在，如果工件保持静止，砂带轮将沿弹簧力的方向进给。这意味着叶片所需的抛光深度和表面精度不仅取决于机器人的进给运动，还与弹簧提供的接触力有关。因此，对于精密的砂带磨削，包括机床砂带磨削，进给运动和接触力必须得到协同控制。

2 机器人运动学分析

在机器人砂带磨削过程中，工业机器人和砂带磨削装置分别提供工件的运动和砂带轮的运动。由于二者分属于不同的系统，很难实现它们的协同控制，因而无法保证抛光精度。

图2所示为机器人砂带磨削的运动学关系。其中，坐标系Sa(即Oa-XaYaZa)位于砂带轮的中心，其Za轴沿砂带轮轴线方向，其Xa轴沿水平方向。Sa又称为砂带轮坐标系。由于砂带轮为圆形，因此为了简化模型，可以忽略其转动对进给过程的影响。

图2 机器人砂带磨削的运动学关系

坐标系Sb(即Ob-XbYbZb)固定在机器人基座上，坐标系Sa固定在砂带轮上，两个坐标系对应轴的方向相同，可将每个轴中心偏移量设为Ex、Ey、Ez。根据文献[19],Sa和Sb坐标系之间的坐标变换矩阵可表示为：

(1)

坐标系Sh(即Oh-XhYhZh)为机器人末端执行器坐标系(法兰盘坐标系)。机器人基坐标系Sb(即Ob-XbYbZb)与末端执行器坐标系Sh之间的坐标变换,由机器人的结构参数和机器人的每个关节角度θi(i=1,2,3,4,5,6)共同决定。一般情况下，由于各相邻的关节角都是耦合的，因此很难算出每个关节角的度数。然而，工业机器人的结构是经过标准化设计的，根据六自由度机器人的D-H建模方法[20]，可建立图3所示的机器人连杆坐标系组，求机器人基坐标系Sb与末端执行器坐标系Sh之间的坐标变换关系。表1所示为机器人的D-H参数。

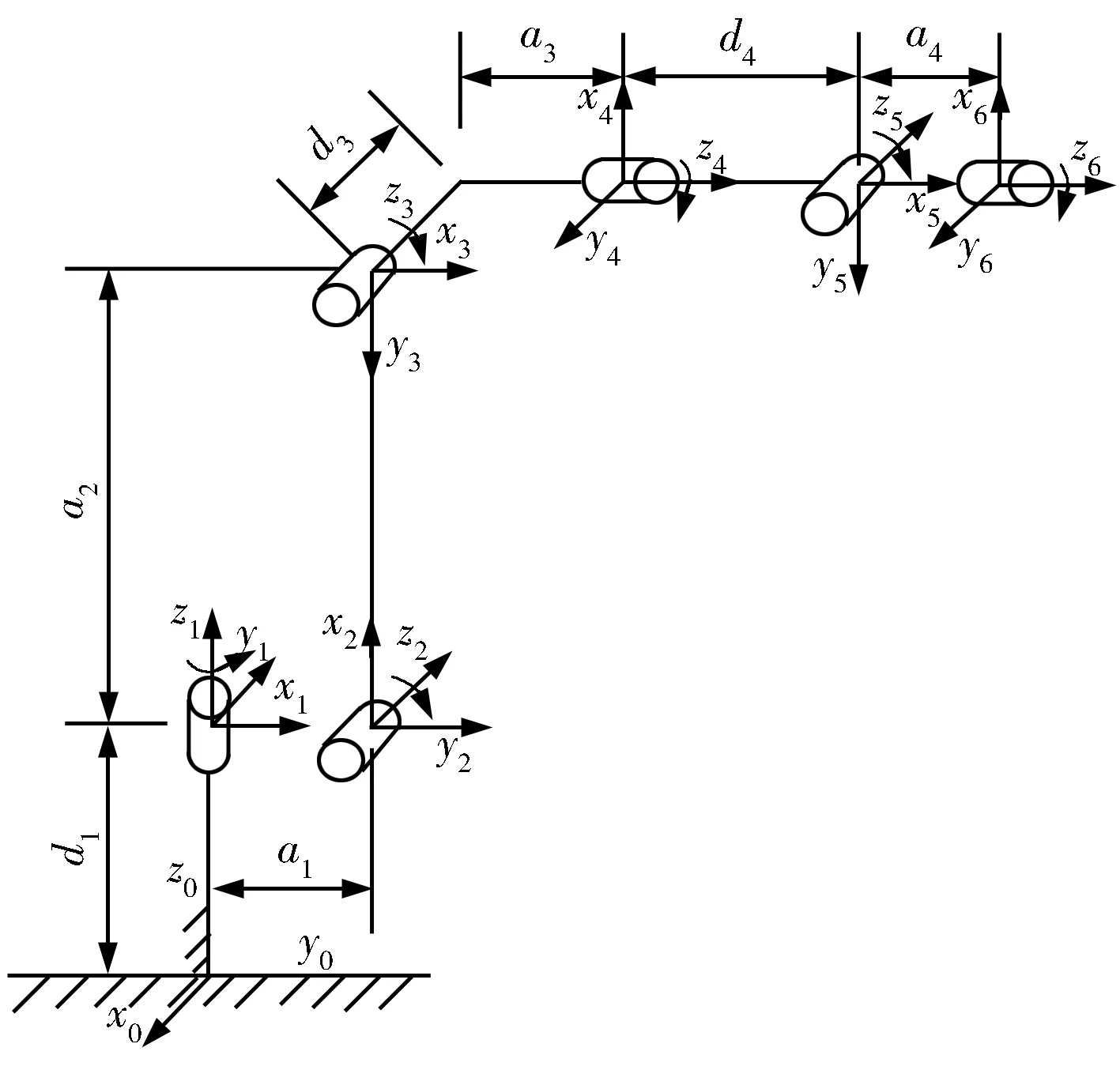
图3 机器人连杆坐标系组

表1 机器人的D-H参数

机器人基坐标系Sb与末端执行器坐标系Sh之间的坐标变换矩阵为：

(2)

式中：

坐标系Sw(Ow-XwYwZw)附着在工件上。这里将其简称为工件坐标系。其中，坐标系Sh、Sw与二者变换矩阵Mwh之间的坐标系转换关系是恒定的，由磨削装置确定。

根据文献[21]，可推导出从磨削装置坐标系Sa(即Oa-XaYaZa)到工件坐标系Sw的变换矩阵，即

Mwa=MwhMhbMba

(3)

由此可得：

(4)

式中，Mwh为坐标系Sw和Sh之间的变换矩阵。

联合式(2)和式(4)，则可求得机器人每个关节的角度[22]θi(i=1,2，…，6)。

3 机器人运动学求解

图4所示为砂带磨削航空发动机叶片表面的接触形态。

图4 砂带磨削航空发动机叶片表面的接触形态

实践中通常将直纹面的曲面定义为：

(5)

(6)

根据微分几何学，直纹面某点处两个法曲率方向为该点处两个正交方向。若叶片毛坯在磨削过程中分别沿母线方向和导向曲线方向运动，则通过式(6)可求出曲面在v、u方向上的法曲率Cv、Cu，且可进一步求得法曲率半径ρv、ρu。为了避免毛坯表面与砂带轮之间的干涉，必须让砂带轮轴线方向与导向曲线的方向一致，且ρw和ρv必须满足以下条件：

ρw<ρv

(7)

(8)

本文提出的倾斜进给方法中，砂带轮坐标系Sa相对于坐标系SB的ZB轴方向的倾斜角为ε。因此，SB和Sa之间的坐标变换关系可表示为：

(9)

类似地，工件坐标系Sw和砂带轮坐标系Sa之间的坐标变换关系可表示为：

Maw(ε)=MaB(ε)MBw(u,v)

(10)

将式(10)代入式(4)中求解，可推导出机器人各关节角度的计算式，即

(11)

4 倾斜角ε与磨削余量的关系

根据普雷斯顿(Preston)经典的基本抛光方程，砂带磨削的材料去除率[24]可表示为：

vh(t)=dh(t)/dt=Kvf(t)Fn(t)

(12)

式中：h(t)为磨削深度;t为磨削时间；K为修正系数；vf(t)为砂带轮相对于叶片毛坯的运动速度；Fn(t)为磨削压力。

由于砂带轮是倾斜的，因此Fn(t)=Fc(t)cosε(这里，Fc(t)为磨削的进给力)，有

vh(t)=Kvf(t)Fn(t)=Kvf(t)Fc(t)cosε

(13)

以磨削深度对磨损时间的积分为例，有

(14)

在一般的磨削过程中，材料去除量可表示为:

h′(t)=KFc(t)cosεsv(t)

(15)

式中，sv(t)为沿母线方向的弧长。它也可表示为：

(16)

因此，磨削时间可以由待抛光表面的参数重新定义，即

t=sv(u,v)/vf(t)

(17)

将其代入式(15)可得：

(18)

推导后，倾斜角可以表示为：

(19)

5 抛光残余量插值法

在叶片坯料的测量过程中，可得到一系列残余点。将这些残余点定义为hi,j(i=0,1，…，Ni;j=0,1，…，Nj)，可表示为：

(20)

式中，矩阵元素hi，j对应于每个点的法向偏差。

由于偏差矩阵只提供实际残余点的离散信息，因此本文参考文献[25],采用一种基于测量离散点的残片插值分段多项式方法,使插值曲面与矩阵Δh的各点相交且无任何拟合误差，以保证离散点符合二阶连续条件。所得多段高阶多项式曲面插值的残差如图5所示。

图5 以多段高阶多项式曲面表示的插值的残差

多段高阶多项式的每个曲面可表示为:

hi,j(x,y)=(Ai,jx+Bi,j)(Ci,jx+Di,j)(Ei,jx+Fi,j)(Gi,jx+Hi,j)(Ii,jy+Ji,j) (Ki,jy+Li,j)(Mi,jy+Ni,j)(Ri,jy+Si,j)

(21)

式中：i=1，2，…，Ni-1;j=1，2，…，Nj-1；Si,j为从点Pi,j，Ai,j，Bi,j，Ci,j，Di,j，Ei,j，Fi,j，Gi,j，Hi,j，Ii,j，Ji,j，Ki,j，Li,j，Mi,j，Ni,j，Ri,j开始的曲面段中每个曲面段的系数;x,y分别表示曲面的u方向和v方向。

不同曲面的一阶偏导和二阶偏导可表示为：

(22)

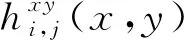
(23)

统计发现，式(23)中共有16个独立方程，与式(21)中待定系数的个数一致，这意味着这16个参数均可以求解。

对比多段高阶多项式的每个曲面hi,j(x,y)函数，可得到偏差面，即

(24)

6 实 验

本文以航空发动机叶片的磨削加工为例，首先利用三坐标测量机测得叶片坯料余量的分布；其次，根据抛光残余量插值法，拟合插值叶片表面残余量；然后根据公式计算每个点的倾斜角度；最后在完成机器人磨削装置的系统搭建后，对叶片进行磨削抛光。采用普通磨削方法和倾斜进给方法磨削叶片边缘的磨削效果、磨削效率的对比情况如表2所示。

表2 普通磨削和倾斜进给磨削叶片边缘的磨削效果、磨削效率的对比情况

分析表2可知，磨削前的叶片坯料边缘余量分布是极其不均匀的；采用普通磨削方法磨削后，叶片前后缘的残余量均超出了公差范围，磨削效果较差；采用倾斜进给方法磨削后，叶片前后缘的残余量均在公差范围之内，且叶片边缘形状趋近于圆弧状的理论形线，未出现偏头、方头、尖头、缩颈等典型的不规则形状，磨削效率也有一定的提高。可以认为，采用倾斜进给磨削方法降低了叶片凹面和凸面的表面粗糙度。某航空发动机叶片抛光前后的表面粗糙度对比见图6。

(a) 抛光前后的叶盆

(b) 抛光前后的叶背

整个磨削过程是通过工业机器人的联动控制来实现的。浮动压力磨头上的压力传感器显示，磨削过程中磨削装置所受的力是恒定的。

7 结束语

针对机器人系统与负载系统协同工作困难的问题，本文提出了一种机器人砂带磨削的倾斜进给方法，通过改变砂带轮轴线与曲面法线的夹角来改变法向载荷，使机器人系统能够控制机器人的位置和负载，从而解决机器人系统和负载系统的协同问题。本文的磨削实例证明，机器人磨削的倾斜进给加工方法是可行的，能够通过改变法向载荷使切向力发生变化。后续应重点研究倾斜进给磨削方法对磨削作用的综合影响。