致密油藏压裂双水平井参数优化研究
2021-02-16胡景宏余国义
胡景宏,陈 琦,余国义,吕 杨
(1.中国地质大学(北京)能源学院,北京 100083;2.非常规天然气地质评价与开发工程北京市重点实验室,北京 100083;3.中国石化西北油田分公司采油一厂,新疆 轮台 841600;4.中国石油国际勘探开发有限公司,北京 100034;5.中国石油长庆油田分公司第五采气厂,陕西 西安 710018)
随着世界范围内常规油气藏开发逐渐进入中后期,开发难度增大。国内外的研究开始更多地关注于非常规油气藏。致密油藏是一种典型的非常规油藏,其资源量丰富,是常规油藏储量的2.5 倍[1-3]。近年来,我国新增探明油气资源以低渗透致密油藏为主;致密储层油气占总开采油藏的比例也在逐年增加[4]。因此,非常规致密油藏开发潜力巨大,前景广阔。随着水力压裂技术的发展,分段压裂水平井技术已经在非常规储层开发中取得良好效果。
为了进行合理的压后产能预测,国内外学者提出了不同的分段压裂水平井解析计算模型。国外学者对此研究较早,根据水电相似原理和有效井径模型,推导了低渗各向同性油藏分段压裂水平井产能方程,提出了有限导流能力压力动态分析的半解析半数值模型[5-7];国内学者也进行了大量关于水平井产能计算的研究,以点汇定流量压降公式为基础,结合复位势理论和空间压力的叠加原理得到考虑裂缝干扰的致密油多级分段压裂非稳态产量计算公式[8-10],或者根据等值渗流阻力法及水电相似原理、当量井径模型以及耦合求解和边界积分方法建立大量精细描述分段压裂水平井产能的数学模型[11-14]。
但是相对于理论模型,实际情况更为复杂。因此,人们通过数值求解和数值模拟提出了大量关于水平井新的计算及优化模型[15-17],根据所研究不同区块的地质特点,简化假设条件,建立油水两相渗流系统,得到较符合实际的油藏—裂缝数学模型[18-20]。但是对于多水平井或双水平井产量随裂缝和水平井筒参数的变化规律研究较少,现场实际生产缺乏相关理论指导。
为研究分段压裂双水平井产量的影响因素并进行工程参数优化。首先,基于渗流力学理论,建立了三维两相数学模型;其次,参考实际区块参数,建立双水平井模型,并综合分析裂缝参数和水平井筒参数及地层因素对水平井产能的影响;最后,使用极差分析法分析了地质及工程因素对水平井产能的影响程度。
1 数学模型的建立
1.1 假设条件
目标区块油藏水平倾角不大,油藏厚度较小,且为分段压裂,隔离射孔的作业方式,因此不考虑流体从地层直接流向水平井的过程,现场生产制度为油井定压生产。数学模型在计算之前采用如下假设:基质—裂缝系统中流体为两相微可压缩流体,并且做等温不稳定渗流,忽略重力和毛管压力影响。由于裂缝所在的平面会沿最小主应力方向展布,因此裂缝为垂直裂缝,并假设裂缝高度大于油层厚度,即有效裂缝高度与油层厚度完全相等,并且裂缝在水平井两端的长度相等,不考虑裂缝不对称情况。数学模型中,油井定为最小井底流压生产,油藏区块是一个上下界面封闭的“水箱”式均质地层。不考虑流体在井筒中的压力降落。
1.2 基质流动模型
油藏基质中考虑启动压力梯度的油水两相渗流基本微分方程[18-19]为:
{▽·[KKmroρoμo(▽Po-γo▽D-Go)]+qom-τomf=∂∂t(φρoSo)m
▽·[KKmrwρwμw(▽Pw-γw▽D-Gw)]+
qwm-τwmf=∂∂t(φρwSw)m
(1)
其中:K为基质渗透率,μm2,Kmro、Kmrw分别为基质的油相相对渗透率、水相相对渗透率;ρo、ρw分别为地层油、地层水密度,g/cm3;μo、μw分别为地层油、地层水黏度,mPa·s;Po、Pw分别为油相、水相压力,MPa;γ为流体重度,γ=ρg,γo、γw分别为地层油、地层水重度,N/m3;D为以油层顶面为基准向下的深度,本文取油藏厚度,m;t为生产时间,天;φ为地层孔隙度;So、Sw分别为含油、含水饱和度;Go、Gw分别为油相、水相的启动压力梯度,MPa/m,qom、qwm为基质所在网格点的源汇流量,注入为正,采出为负,m3/d,τomf、τwmf为基质到裂缝的窜流项,m3/d;下标m表示基质。
1.3 裂缝流动模型
油藏裂缝中油水两相渗流基本微分方程[18]为:
{▽·[KfKfroρoμo(▽Po-γo▽D-Go)]+
qof+τomf=∂∂t(φρoSo)f
▽·[KfKfrwρwμw(▽Pw-γw▽D-Gw)]+
qwf+τwmf=∂∂t(φρwSw)f
(2)
其中:Kf为裂缝区域的渗透率,μm2;Kfro、Kfrw分别为裂缝内油相相对渗透率、水相相对渗透率;qof、qwf为裂缝所在网格点的源汇流量,注入为正,采出为负,m3/d;下标f表示裂缝。
1.4 辅助条件
考虑流体和孔隙压缩性的状态方程:
{φ=φ0+Cf(P-P0)ρ=ρ0eCL(P-P0)=ρ0[1+CL(P-P0)]
(3)
油藏压力下降过程中,油藏渗透率与油藏压力的表达式为:
K(P)=K0e[αk(P-P0)]
(4)
油藏压力上升过程中,油藏渗透率与油藏压力的表达式为:
K′(P)=K′0e[α′k(P-P0)]
(5)
其中:P为原始地层压力,MPa;P0某一参考压力,MPa;φ0为参考压力P0时的孔隙度;ρ0参考压力P0时流体密度,g/cm3;Cf为孔隙压缩系数,MPa-1;CL为对应流体的压缩系数,MPa-1;K(P)、K′(P)分别为油藏压力下降和上升过程中某一压力下的渗透率,K0、K′0分别为参考压力下渗透率μm2;αk、α′k为应力敏感系数。
2 双水平井产能影响因素分析
根据西北地区某油藏的地质及生产数据,对基质-裂缝系统进行统一的网格划分,利用局部网格加密方法[20]建立精细压裂双水平井数值模拟模型。
数值模拟模型综合考虑了裂缝参数、水平井段参数和基质参数对双水平井产能的影响。使用控制变量方法对每个影响因素单独分析得到相应的定量变化规律,再使用多因素正交分析方法对重要的几个参数进行影响量大小排序。其中,应力敏感效应的计算体现在孔隙度和渗透率的变化上。所有模型中,均未考虑裂缝不对称情况,即裂缝长度、间距相等;裂缝所在平面与水平井筒垂直,并且关于水平井筒对称。根据目标区块的地质特点,分段压裂双水平井3D示意图和具体地层和工程参数见图1和表1。

表1 地质参数和工程参数表Table 1 Geological and engineering parameters used in the modelling
图1 分段压裂双水平井3D示意图Fig.1 Simulation model with dual horizontal well in tight oil reservoirs
启动压力的存在直接影响致密油藏流体流动规律[21-22]。在数值模拟计算中测量和计算油水相对渗透率曲线的方法有很多[23-24],包括解析计算模型和改进的实验方法等[25-27]。本文使用应用最广泛的JBN方法测量岩心相对渗透率,得到该区域基质流动的相渗曲线。
假设在分段压裂施工后,油藏内流体由基质流向裂缝,再由裂缝流向井筒,基质直接流入井筒的流量忽略不计。在裂缝系统的油水连续性流动方程(公式(2))中,已经给出了由质量守恒确定的油水流量公式,而这些流量来自基质系统,并为之所限制,此时的油水流量可以反映出裂缝中的油水两相流动情况。相对于低渗/特低渗的基质系统,裂缝相当于一个高导流通道或者无限导流通道,裂缝的导流能力不再是限制流体流动的因素,反而是基质的供液能力限制了流体流动能力和油井产量,裂缝内流体的相对渗透率曲线近似为范围从0到1的两条相交直线。本文中致密油藏中岩心基质渗透率如图2。
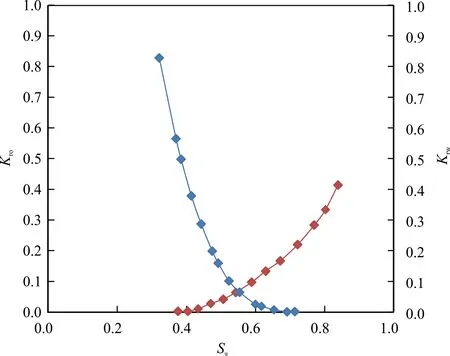
图2 油水两相相对渗透率图Fig.2 Oil-water relative permeability curve of the cores from tight oil
2.1 工程参数对双水平井产能的影响
裂缝是分段压裂水平井供油的主要位置,裂缝参数对于水平井产能有巨大影响[9,15],水平井筒长度和水平井筒之间的距离也会影响水平井产能。通过控制其他变量不变,为便于研究裂缝几何参数和特征对水平井产量的影响,在因素分析过程中,没有考虑启动压力的影响,再逐一确定多段分级压裂水平井产量随裂缝参数以及水平段参数变化而产生的影响,进而得到每个影响因素的最优范围,指导区域致密油藏开发设计。
2.1.1 裂缝长度
控制其他裂缝参数不变,在水平井筒长度固定的情况下,以垂直对称裂缝建立数值模拟模型,双水平井生产300 天后的累积产量如图3所示。

图3 不同裂缝条数时300天的累积产量随裂缝长度变化Fig.3 Cumulative production of 300 days and variation with fracture length and different fracture number
可以看出,在水平井筒间距设置为固定值时,不同裂缝条数时裂缝半长增加,水平井产量随之增大,但是随后水平井产量的增加幅度变化开始趋于平缓。这是因为一方面裂缝长度增加,裂缝控制的泄油面积增大;由于水平井井筒间距不变,随着裂缝长度的增加,裂缝尖端间距变小,不同水平井之间裂缝干扰增强。不同裂缝条数下,累积产量在裂缝半长为150 m 后增加变缓,从而可以得到每个裂缝条数下最优的裂缝半长在150 m 左右。
2.1.2 裂缝条数
同样控制其他裂缝参数不变,固定水平井筒长度,以垂直对称裂缝建立数值模拟模型,不同裂缝长度情况下,生产300 天后的累积产量变化如图4。

图4 不同裂缝长度时300天的累积产量随裂缝条数变化Fig.4 Cumulative production of 300 days and variation with fracture number and different fracture length
可以看出,不同裂缝长度条件下,水平井产量随裂缝条数的增加而增大,并且都在7条裂缝时出现水平井产量增加明显变缓的现象。由于水平井井筒长度固定不变,水平井筒上裂缝均匀分布,裂缝条数增加之后,裂缝密度变大,于是裂缝控制体积出现重叠,在水平井生产之后压降漏斗出现叠加范围,影响了水平井产量的增加幅度。
为更直观地看出双水平井产量随裂缝条数的变化情况,并找到裂缝条数增加时缝间干扰对产量增加幅度影响的临界点,从而寻找到最佳的裂缝条数范围。建立了裂缝半长为150 m 的不同裂缝条数的模型,得到图5的结果。水平井裂缝条数增加到5条后,水平井稳产之后的单日产量明显增加变缓;水平井裂缝条数增加到7 条后,水平井稳产之后的单日产量甚至不再增加。因此,开采本区域的双水平井裂缝条数应该控制为5~7 条。
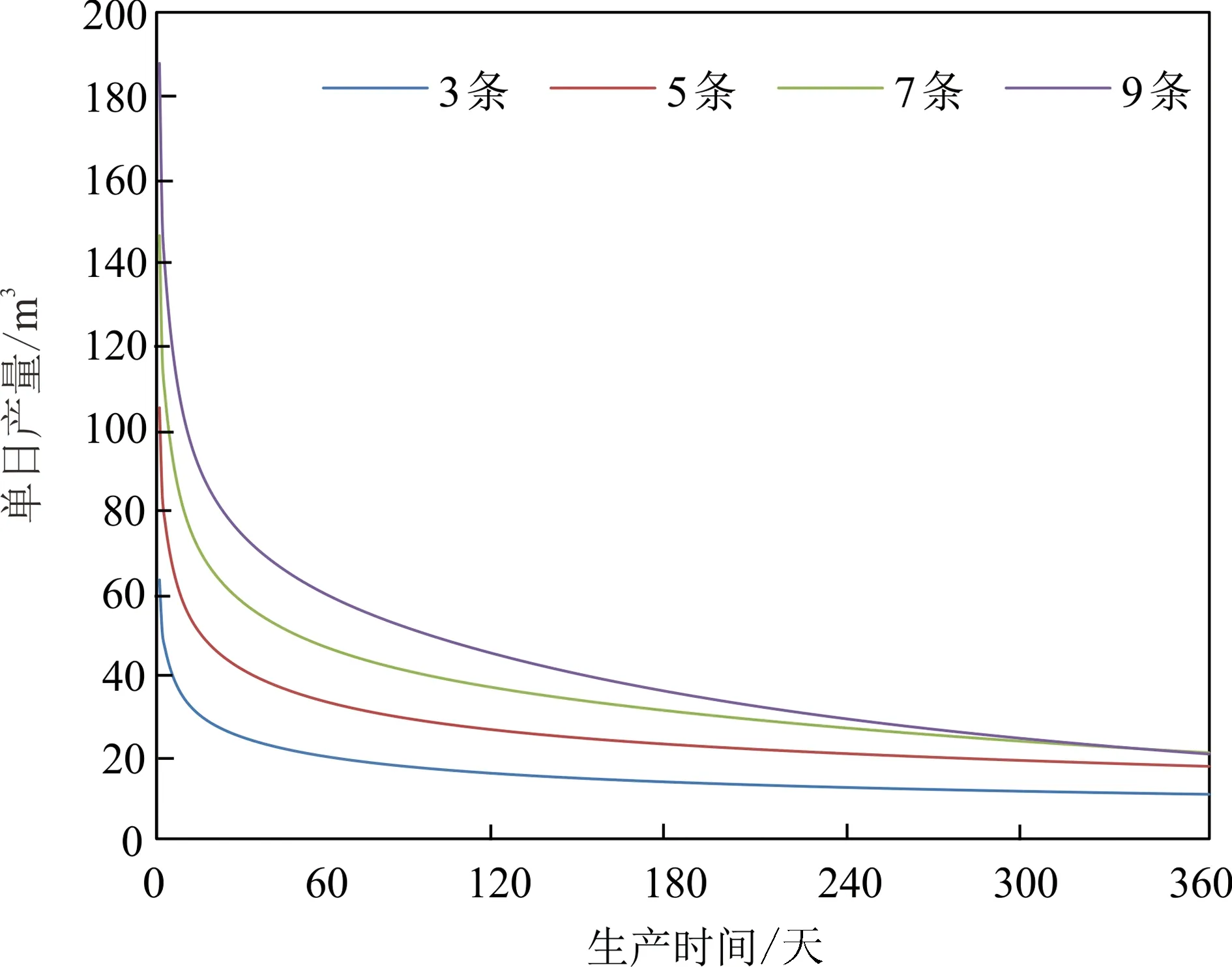
图5 不同裂缝条数时水平井单日产量随时间变化图Fig.5 Daily production of dual horizontal well and variation with production time and different fracture number
2.1.3 裂缝导流能力
以7 条半缝长为150 m 的垂直对称裂缝为例,通过确定裂缝宽度改变裂缝渗透率使裂缝导流能力发生改变,研究不同裂缝导流能力对水平井产量的影响。水平井生产300 天后的累积产量和单日产量如图6所示。
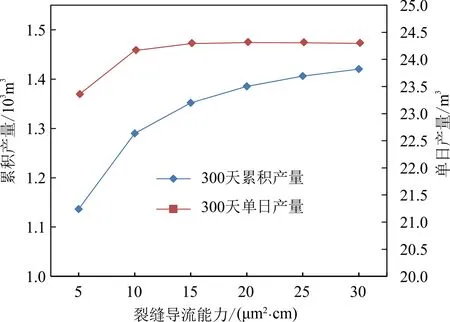
图6 水平井产量随裂缝导流能力变化图Fig.6 Cumulative production of 300 days and variation with fracture conductivity
裂缝导流能力增加使得双水平井的累积产量和单日产量都随之增大,此区域人工裂缝导流能力在5~15 μm2·cm之间变化时,水平井产量增加的幅度较大;人工裂缝导流能力在15 μm2·cm之上变化时,水平井产量增加变慢,甚至不再增加。这是因为基质渗透率和孔隙度没有明显改变,使基质的流体流动能力限制了流体流入裂缝平面的流量,于是即便人工裂缝导流能力继续增加,但裂缝内流体无以为继,出现产量不再增加的情况,即产量曲线出现拐点。由图6可得,此区块在压裂裂缝导流能力增加到10 μm2·cm 时,产量增加明显变缓;在压裂裂缝导流能力增加到15 μm2·cm 时,产量基本不再变化。开采此区域的最优人工裂缝导流能力为10~15 μm2·cm。
2.1.4 水平井筒长度和间距
水平井筒的长度和间距也会对水平井的产量产生巨大影响。在上述讨论优选的最佳裂缝参数条件下建立不同井筒长度和间距的数值模拟模型,模拟结果如图7和图8所示。

图7 水平井产量随水平井筒长度变化图Fig.7 Cumulative production of 300 days and variation with horizontal wellbore length
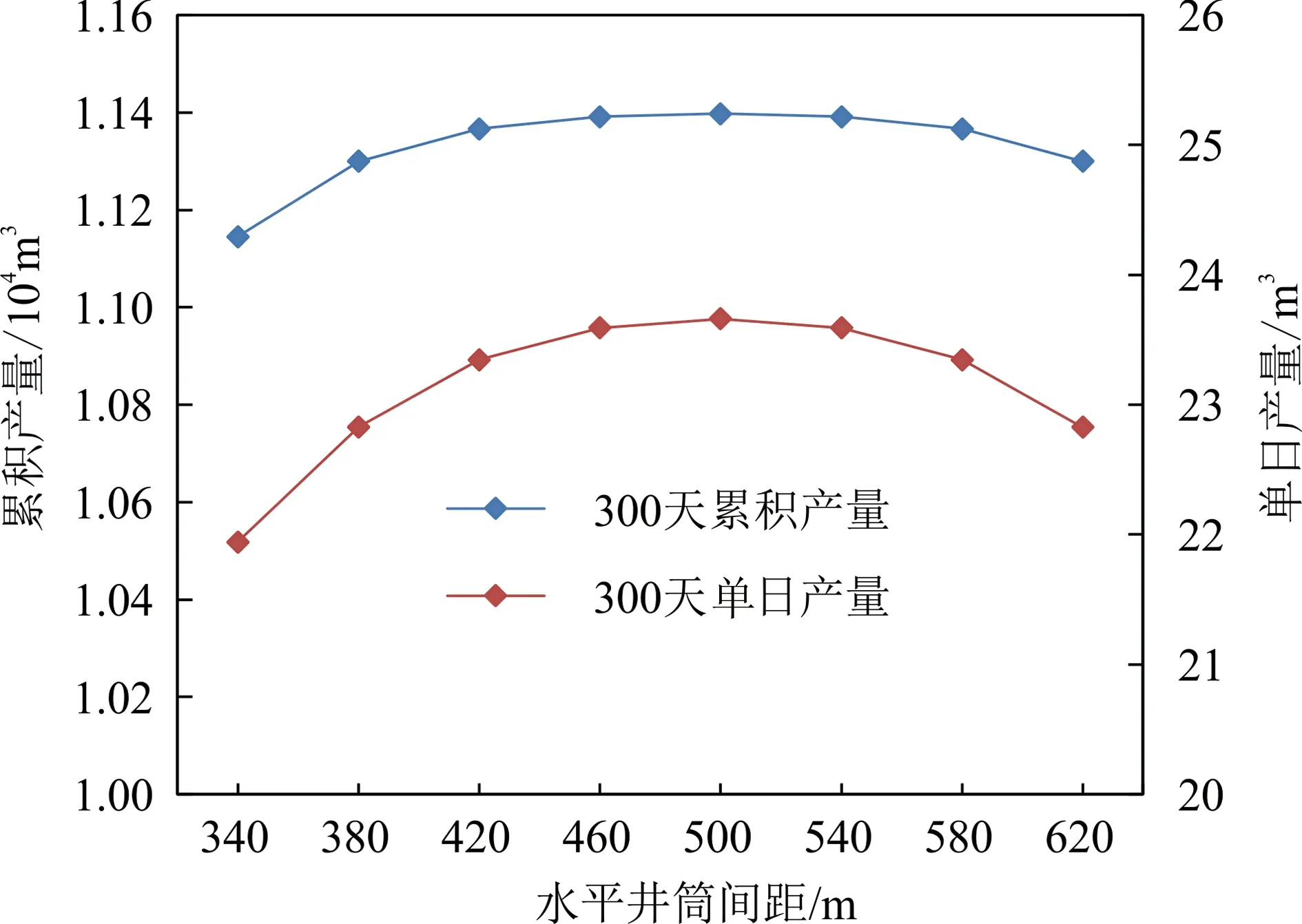
图8 水平井产量随水平井筒间距变化图Fig.8 Cumulative production of 300 days and variation with horizontal wellbore spacing
水平井筒长度增加,双水平井的产量明显增大,但在一定程度后增加变缓。这是因为裂缝条数设置为定值时,水平井筒长度的增加会使裂缝之间的距离增大,缝间干扰变小,单条裂缝控制面积增加,水平井产量增加,但是由于油藏基质孔隙度和渗透率较低,基质供液能力有限,所以水平井产量增加变缓。可以看出,在水平井筒增加到1 200 m 时,水平井单日产量和累积产量增加幅度明显变小;在水平井筒增加到1 350 m 时,水平井单日产量和累积产量基本不再增加。因此,此区块开发水平井筒长度应该为1 050~1 350 m。
在一定范围内,水平井筒间距的增加使得双水平井产量出现先增大再减小的趋势,并且水平井产量增加的幅度大于减小的幅度。因为裂缝半长保持不变,水平段之间距离增加时,两个水平井上裂缝尖端距离也随之增加,两口井上的裂缝相互之间的干扰变小,并且裂缝控制体积变大使得产量明显增加。但是因为油藏规模确定不变,水平井筒间距的继续增加会使得水平井越来越靠近油藏边缘,水平井靠近油藏边缘一侧的半裂缝控制储量减小,因此水平井产量开始下降。根据图8,在水平井筒间距增加到420 m 时,水平井单日产量和累积产量增加都开始变缓;水平井筒间距增加到500 m 时,水平井单日产量和累积产量都开始下降。所以此区块应在油藏中部打井,并且增加水平井筒间距到400~500 m。
2.2 地层参数对双水平井产量的影响
由应力敏感导致的渗透率和孔隙度变化和致密储层具有的启动压力梯度对水平井产量有很大的影响,为了直观描述水平井产量变化情况,便于增加正交试验方法中的试验因素和水平以比较各个因素对产量影响的权重,因此研究了基质渗透率、孔隙度和启动压力梯度对水平井产量的影响。根据上述讨论得到优化的裂缝参数和井筒参数建立不同的数值模拟模型,得到如图9、图10和图11的结果。

图9 水平井产量随基质渗透率变化图Fig.9 Cumulative production of 300 days and variation with matrix permeability

图10 水平井产量随基质孔隙度变化图Fig.10 Cumulative production of 300 days and variation with matrix porosity
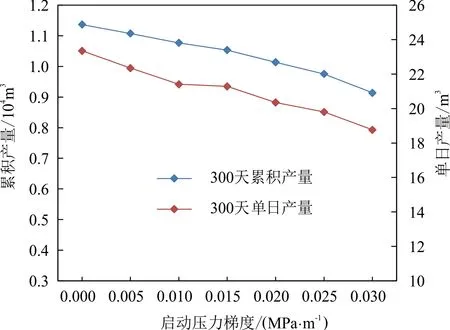
图11 水平井产量随启动压力梯度变化图Fig.11 Cumulative production of 300 days and variation with starting pressure gradient
国内研究人员进行了大量关于启动压力梯度的研究,窦宏恩、王晓冬和李爱芬等人明确指出了低/特低渗油藏存在启动压力梯度,并且相同的地层条件下启动压力梯度应该是相近的,然后他们给出了启动压力梯度的一般计算范围和相应的计算方法[21-22,28]。宋付权、郝鹏程和谭晓华等人提出了实验确定启动压力梯度的方法,并给出了经验公式和理论验证,找到了启动压力梯度和相对渗透率的关系[29-31]。郝斐、高辉等人利用精密仪器测量启动压力梯度并给出拟合的经验公式[32-34]。本文在一般的启动压力梯度范围内,将相对渗透率范围代入理论公式计算出本区域启动压力梯度范围,并利用若干次随机实验验证计算结果的可靠性得出本区块的启动压力梯度范围为0~0.03 MPa/m,大多数岩心启动压力梯度为0.005~0.010 MPa/m。据此,进行一般性的规律研究。
基质渗透率和孔隙度的增大使得双水平井的单日产量和累积产量均开始增大,并且增加明显。但是由于工程参数已经确定,因此也会同样出现产量增加变缓的情况。所以应力敏感造成的基质孔隙度和渗透率的变化对双水平井的产量影响较大。
由图11可知,考虑启动压力梯度使得双水平井的产量减小,减小的趋势近乎是一条斜率比较低的直线。启动压力梯度代表流体在孔喉中开始流动时所需的压力,启动压力梯度的增加意味着流体流动难度的上升,即生产压差随之减小,因此出现水平井产量降低的现象。
3 多因素正交分析
正交设计方法是一种能够以花费小(精简试验次数)、科学性高(数据点分布均匀)、多样性分析(可选分析方法多)这些特点完成试验结果合理分析和科学问题合理解决的数学方法,本节分析影响水平井产量的各个参数的正交设计方法具体的步骤如图12。
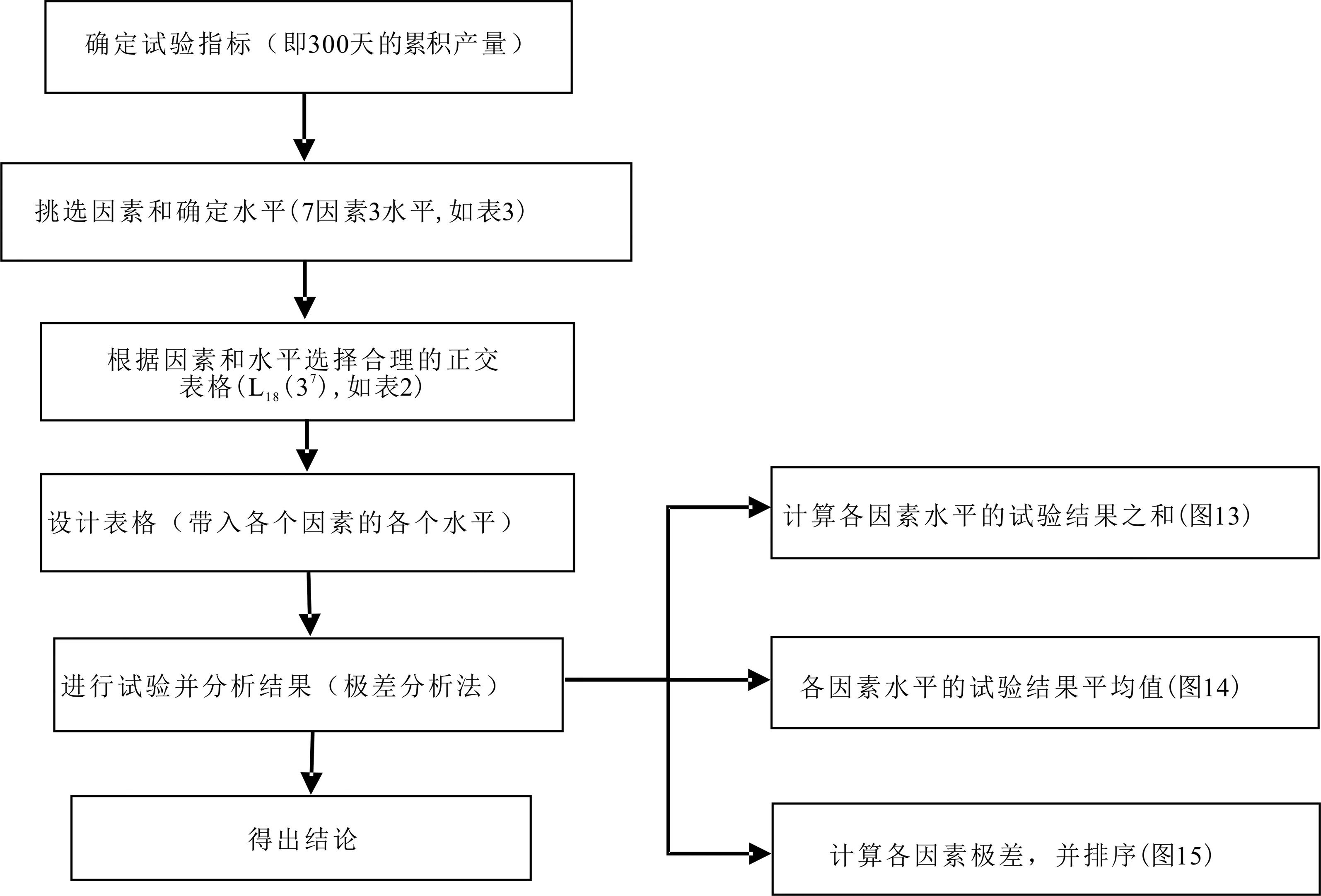
图12 正交设计方法的步骤Fig.12 Procedure of the orthogonal design method
针对本区块地质条件,根据上述讨论,设计了一个7因素,每个因素3水平的正交表格(表2):L18(37)。利用数值模拟模型和局部网格加密方法计算每个方案生产300天后的累积产量,作为试验结果,即试验指标,用来比较各个因素对双水平井产能影响程度的大小。
7因素分别是压裂水平井工程参数,包括裂缝条数(水平设置为5、7、9条),裂缝长度(水平设置为110 m、150 m、190 m),水平井筒长度(水平设置为600 m、900 m、1200 m),水平井筒间距(水平设置为340 m、420 m、500 m)以及裂缝导流能力(水平设置为5 μm2·cm、15 μm2·cm、25 μm2·cm);地质因素包括基质孔隙度(水平设置为0.06、0.09、0.12)和渗透率(水平设置为0.05×10-3μm2、0.1×10-3μm2、0.15×10-3μm2)(表3)。按照图12中的正交设计方法的步骤以及表2和表3的设计方案进行水平井各个参数对于产量的影响因素研究,最终各个因素对于水平井产量影响大小排序结果如图13、图14和图15所示。

表2 影响双水平井产能的试验因素设计方案Table 2 Orthogonal test design of influencing factors on productivity

图13 各因素水平的试验结果柱状图Fig.13 Bar charts of test results for each factor level

表3 影响双水平井产能的试验因素Table 3 Test factors influencing the productivity of dual-level wells

图14 各因素水平的试验结果均值柱状图Fig.14 Average bar chart of testing results for each factor level

图15 影响水井产量因素的极差分布图Fig.15 Range analysis results of influencing factors on well production
在研究的影响水平井产能的7个因素中,基质孔隙度、水平井筒长度和基质渗透率对水平井产能贡献最大,并且也最能影响其产量。储层条件的改善和优化能够极大地增加水平井产量和产速。在所有的工程参数中,由于水平井筒长度的增加大幅度增大了单条裂缝的储量控制体积,因此其影响产能最为明显。可以得出结论:在此区块油层渗流条件下,多水平井开发时,应该保持裂缝控制体积的同时,将水平段向油藏边缘适当移动,增加水平井段之间的距离,以减小裂缝干扰,增加井筒长度,均匀布缝并且延长裂缝半长但要保持裂缝尖端距离。
4 结 论
(1)双水平井产量随着裂缝条数、长度的增大而增加,并且会出现增加幅度变小的现象;根据产量变化规律可以确定此区块最优裂缝条数为5~7 条,最优裂缝长度为260~300 m。双水平井的产量会随着人工裂缝导流能力的增大而迅速增加,与水平井产量随裂缝条数、长度变化规律不同的是,其产量的增加会迅速变缓;此区块在裂缝导流能力增加到10 μm2·cm时,双水平井产量增加明显变缓,在裂缝导流能力增加到15 μm2·cm时,产量基本不再变化,因此最优裂缝导流能力在10~15 μm2·cm。
(2)双水平井的产量会随井筒长度的增大而增加,同样会出现初始增加幅度较大,后来增加变缓的“黏滞增长”现象;由于在井筒长度增加为1 050 m时,水平井产量增加开始变缓,井筒长度增加为1 350 m时,水平井产量几乎不再增加,所以此区块最优水平井筒长度为1 050~1 350 m。
(3)在油藏区域有限的情况下,双水平井的产量随着井筒间距的增加出现先增大后减小的趋势,并且增大幅度明显大于减小幅度。对于此区块而言,在水平井筒间距增加到420 m时,水平井单日产量和累积产量增加开始变缓;水平井筒间距增加到500 m时,水平井单日产量和累积产量开始下降,所以其合理井距应该为400~500 m。
(4)地层因素方面,双水平井产量变化规律和一般水平井以及直井变化规律类似,其产量与基质渗透率和基质孔隙度都呈正相关关系,并且相对变化幅度较大。本区块启动压力梯度对致密油藏产量具有负面影响,考虑启动压力梯度产量会有所下降,并且随着启动压力梯度的等量增加,产量减小得越快。
(5)针对此区块的地层条件所研究的5个对水平井产量具有比较大的工程影响因素的主次排序为:水平井筒长度>裂缝导流能力>裂缝长度>水平井筒间距>裂缝条数。
