基于神经网络内模的热解反应器温度控制

2021-02-16王志刚

天津理工大学学报 2021年6期

何蒙，王志刚*

（天津理工大学a.天津市先进机电系统设计与智能控制重点实验室，b.机械工程学院，天津 300384）

合理充分地利用生物质能对缓解能源危机，减少环境污染等具有重要意义。热解是开发利用生物质技术手段之一，热解温度关系到产物的产率，因此温度控制对生物质热解工艺具有重要意义。本文中生物质热解反应器的加热装置采用电加热，工作环境复杂，易受外界干扰影响，且其温控系统具有时变性、大滞后和大惯性等特点，对于这类系统采用传统控制方法很难达到理想的控制效果[1]。

比例积分微分控制器（proportional integral derivative control，PID）的控制方法由于结构简单、实现方便，常被应用于加热炉温度控制中，但由于无法建立精确的数学模型，且系统中存在时滞和惯性环节，使传统PID在这类系统中的控制效果不太理想[2-3]。Smith预估控制算法能消除时滞对系统动态性能的影响，常被用于温度控制系统[4]。但它也需要控制对象与对象模型完全匹配，才能达到理想控制效果，这在现实工业生产中难以实现，而且当外部干扰很大时，无法保证系统的稳定性。

内模控制可以看作是Smith预估控制的一种扩展，大大改善了Smith控制器的鲁棒性和抗干扰特性，而且结构简单，可调整参数少，不需要十分精确的数学模型，适用于大时滞系统，因此被专家学者们广泛应用于各种温度控制系统[5-6]。将内模控制与其他控制算法相结合，如在空调冷却水系统中的温度控制采用基于育种算法的内模串级控制器[7]，针对循环水热交换系统中循环水进口温度提出三自由度内模控制器，利用变步长人工鱼群算法对其进行参数调整[8]，将模糊逻辑与内模控制算法相结合，实现控制参数的在线整定[9-10]等。

热解反应器温度控制系统很难建立精确的数学模型，而神经网络可实现任意逼近非线性函数且容错性能良好，广泛应用于非线性系统建模，系统辨识、预测等[11-12]。在温度控制方面，文献[13]对神经元逆模型进行了相关研究，文献[14]采用神经网络辨识技术，建立了系统的数学模型，文献[15]利用神经网络的监督控制修正PID控制参数，文献[16]提出通过神经网络在线辨识得到梯度信息对PID参数进行在线调整。

1 热解反应器温度控制系统

1.1 温度控制原理

生物质热解反应的整个过程在螺旋反应器中进行，反应器采用电加热，当温度上升到设定值时利用控制算法使其保持恒定。

生物质热解反应器温度控制系统，如图1所示。将可编程逻辑控制器（programmable logic controller，PLC）作为下位机，获取温度信号，采用LABVIEW作为上位机的软件平台，设计人机界面，实现各控制指令的输入和温度曲线的绘制。

图1 生物质热解反应器温度控制系统Fig.1 Temperature control system diagram of biomass pyrolysis reactor

温度传感器采集反应器温度数据，并将温度信号送入PLC中，PLC将模拟量转换成数字量送到上位机，LABVIEW根据所测数据绘制的升温曲线，如图2所示。

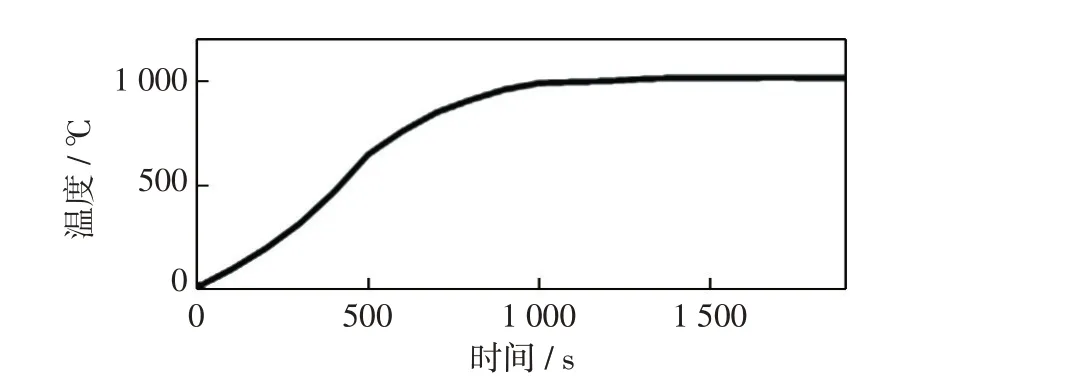
图2 升温曲线Fig.2 Heating curve

1.2 数学模型的建立

由于热解反应器温度控制系统具有非线性、大惯性和大滞后等特点，难以通过机理法规建立数学模型，通常采用实验建模法。根据其升温过程的特点，可以将其数学模型表示成一阶惯性加滞后环节，其公式为：

式中，K为增益，T为时间常数，τ为滞后时间常数。

由Cohn-Coon公式，结合反应器温度响应曲线，求解得出热解反应器温控系统的数学模型，其公式为：

式中，ΔC表示输出响应，ΔM表示输入响应，t0.28表示当温度值为0.280ΔC时对应的时间，同理t0.632表示当温度值为0.632ΔC时对应的时间。

计算得出生物质热解反应器温度控制系统的数学模型，其公式为：

式中，G(s)为传递函数。

2 神经网络内模控制器

考虑到热解反应器温控系统的特点，采用内模控制方法，但当系统非线性较强、滞后时间或外界干扰较大时，控制效果可能不太理想。神经网络可逼近任意非线性函数，且自适应能力强，不依赖被控对象模型。将内模控制与神经网络相结合，可提高系统的控制性能。因此，本文提出将神经网络与内模控制算法相结合，得到神经网络内模控制器（neural network internal model controller，NNIMC）。

2.1 内模控制

内模控制是基于过程数学模型确立的控制方法，内模控制原理如图3所示。

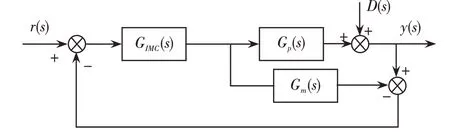
图3 内模控制原理Fig.3 Schematic diagram of internal model control

其中，r(s)为输入信号，GIMC(s)为内模控制器，Gp(s)为被控对象模型，Gm(s)为对象模型，D(s)为未知扰动，y(s)为系统输出。

由图3可以得出设定值和未知干扰输入到输出的传递函数分别为：

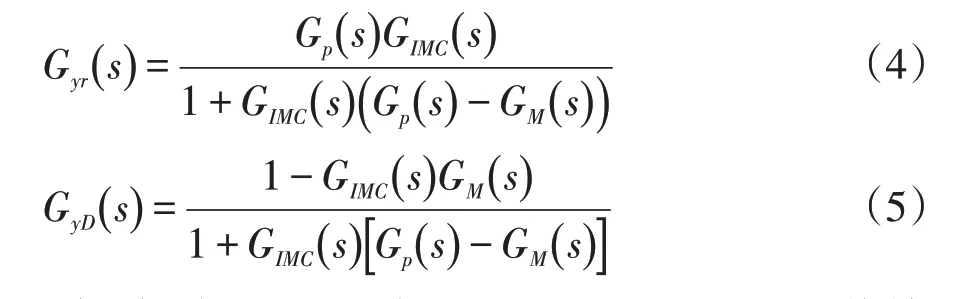
则根据式（4）和式（5）可以得出闭环系统输出响应为：

当模型完全匹配，即GP(s)=GM(s)时，系统闭环输出响应为：

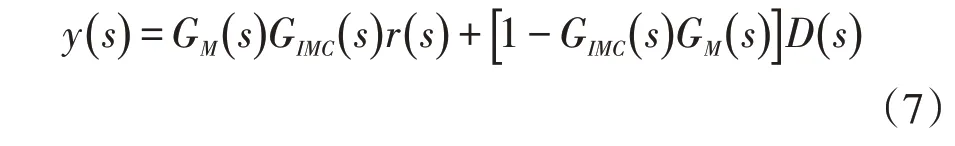
虽然与Smith预估控制器相比，内模控制算法对模型精度要求不太严格，但其也是基于数学模型建立的控制器，当该模型失配，特别是时滞常数相差较大时，控制效果不理想，甚至可能会引发系统振荡。由此，可将神经网络与内模控制算法相结合来改善这一缺点。

2.2 神经网络内模控制

基于神经网络的内模控制系统结构图，如图4所示。

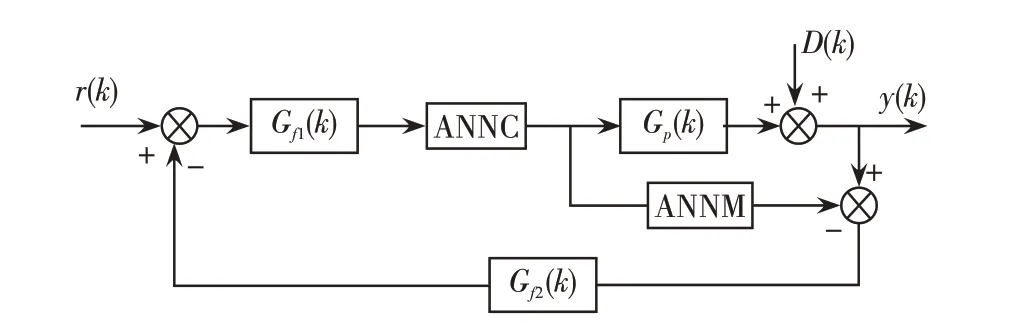
图4 基于神经网络的内模控制系统结构图Fig.4 Structure diagram of internal model control system based on neural network

其中，r(k)为设定值输入，Gf1(k)和Gf2(k)为滤波器，神经网络控制器（artificial neural network controller，AMMC），神经网络模型（artifical neural network model，ANNM）为被控对象模型（神经网络正模型），D(k)为未知干扰。

由图3和图4可知，与传统内模控制结构相比，神经网络内模控制器采用神经网络辨识模型来代替被控对象模型和内模控制器。为了提高系统的鲁棒性和动态性能，在前向通道和反馈回路增加了滤波器。

被控对象模型采用串并联型辨识结构，如图5所示。

图5串并联型辨识结构Fig.5 Series-parallel identification structure

图5可知，所辨识的被控对象模型输入为被控对象输入u(k)和输出y(k)，em(k)为被控对象输出y(k)与被控对象模型输出ym(k)之差，在实际应用中由不断产生的输入输出数据，计算得出em(k)，来在线调整被控对象模型的权值。

内模控制器模型根据采集的被控对象数据，利用神经网络辨识出被控对象模型，用其输出与被控对象输入的差值ec()k来训练内模控制器，神经网络内模控制器辨识结构，如图6所示。

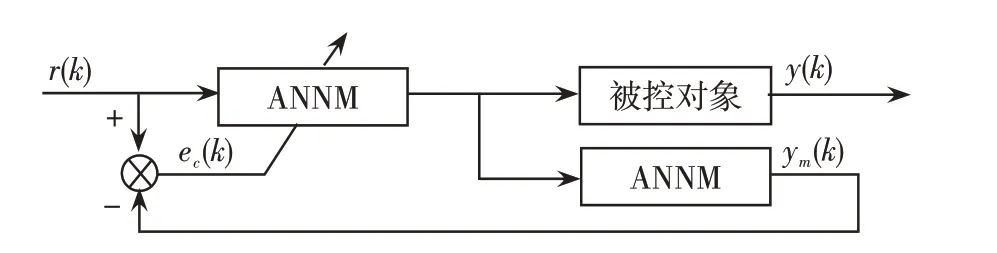
图6 神经网络内模控制器辨识结构Fig.6 Identification structure of neural network internal model controller

在控制器前和反馈回路中分别加入滤波器Gf1(s)和Gf2(s)，其中，Gf1(s)可将误差映射到适当位置，使系统输出响应跟踪设定值，Gf2(s)可平衡未知扰动引起的模型失配，提高控制系统的鲁棒性。

在反应器温控系统中，Gf1(s)和Gf2(s)均采用一阶滤波形式，其公式为：

将上式离散后，可得公式为：

式中，f(s)为滤波函数，μ为滤波器的时间常数，取值范围为0≤μ≤1。

3 仿真分析

式（3）为生物质热解反应器温度控制系统的传递函数。在MATLAB/SIMULINK中建立温度控制系统模型，先后利用BP神经网络对被控对象模型和内模控制器进行辨识，然后在线运行。为了对结果进行验证，本文选取了其他3种方法，分别为内模控制（internalmodelcontrol，IMC）、传统PID和PATHIRAN等[17]的基于内模控制死区补偿（intemal model control dead time compensation，IMC-DTC）方法。为方便进行比较，所有滞后时间常数都取λ=3τ，传统PID中，取P=0.90，I=0.01，D=0.80，文献[17]中所用的IMC-DTC控制，根据其文中所述，取τcl=51.70。在850 s时加入幅值为0.20的阶跃扰动信号。

模型完全匹配时系统输出，如图7所示。

图7 模型完全匹配时系统输出Fig.7 System output when the model matches perfectly

由图7（a）可知，当模型完全匹配时，PID出现超调，超调量为44.203 0%，初始阶段的局部放大图如图7（b）所示，IMC-DTC在638 s达到0.994 6，存在值为0.005 4的误差，在850 s时加入干扰信号后，系统输出的局部放大图如图7（c）所示，可知，IMC-DTC在1 550 s达到0.997 4，存在0.002 6的稳态误差。模型匹配时仿真结果统计，如表1所示。

表1 模型匹配时仿真结果统计Tab.1 Statistics of simulation results when model matching

当模型失配时，将增益K、时间常数T和时滞常数τ分别减少20%时系统输出，如图8所示。

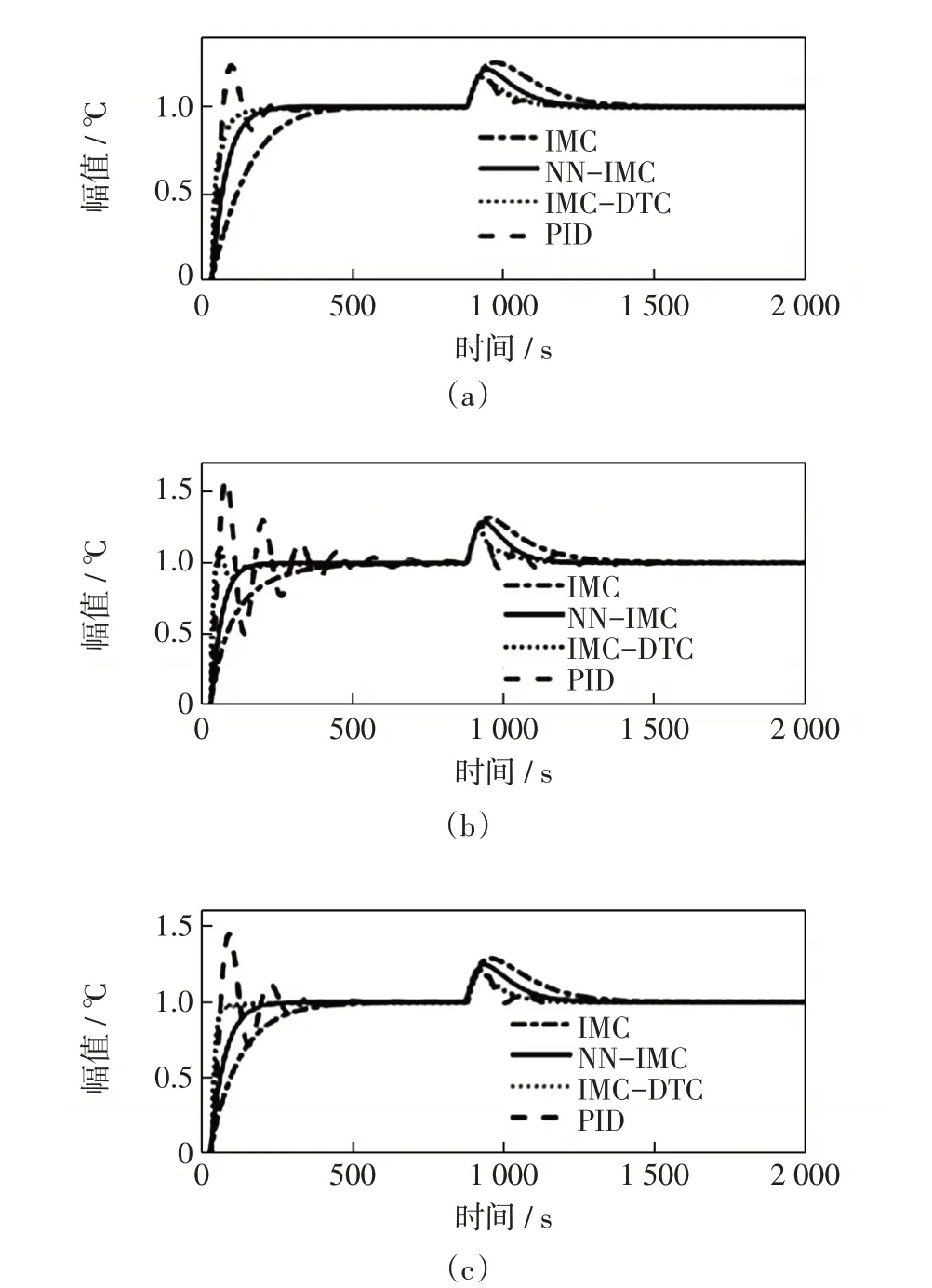
图8 增益、时间常数和时滞常数分别减少20%时系统输出Fig.8 System output when gain，time constant and time delay constant are reduced by 20%

由图8（a）可知，当增益减小20%时，PID控制产生24.375 0%的超调，且IMC-DTC产生了0.006 8的误差。而在加入干扰信号之后，IMCDTC出现值为0.004 0的稳态误差。增益减小20%时仿真结果统计，如表2所示。

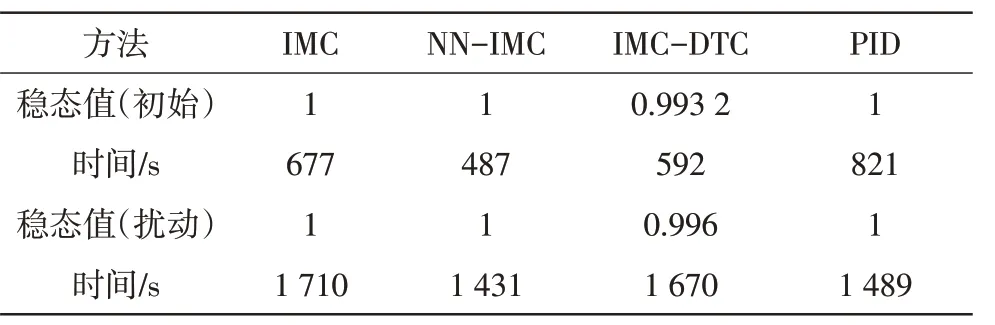
表2 增益减小20%时仿真结果统计Tab.2 Statistics of simulation results when the gain is reduced by 20%

由图8（b）可知，当时间常数减少20%时，PID超调量为57.937 0%，IMC-DTC产生10.640 0%的超调，IMC-DTC存在值为0.005 0的误差。系统存在干扰时IMC-DTC在1 562 s达到0.997 0，即存在0.002 0的稳态误差。时间常数减少20%时仿真结果统计，如表3所示。

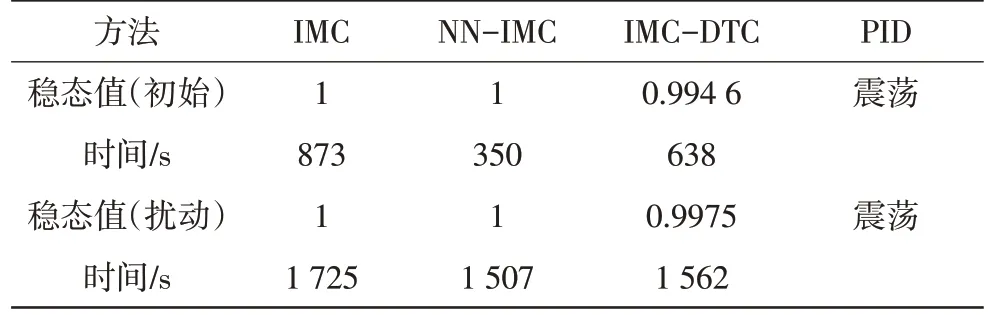
表3 时间常数减少20%时仿真结果统计Tab.3 Statistics of simulation results when the time constant is reduced by 20%

由图8（c）可知，当时滞常数减少20%时，PID超调量为44.203 0%，IMC-DTC存在值为0.005 4的误差。系统存在干扰时，IMC-DTC在1 562 s达到0.997 4，存在0.002 6的稳态误差。时滞常数减少20%时仿真结果统计，如表4所示。

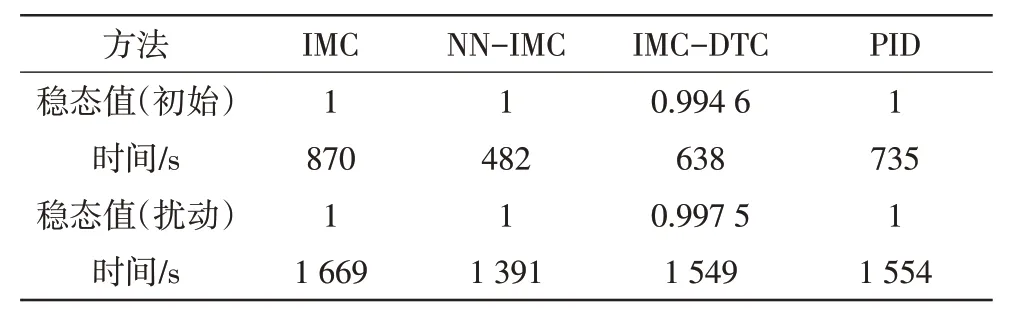
表4 时滞常数减少20%时仿真结果统计Tab.4 Statistics of simulation results when the time delay constant is reduced by 20%

增益，时间常数和时滞常数全部减小20%时，模型完全失配时系统输出，如图9所示。

由图9可知，当模型完全失配时，PID的超调量为53.077 0%，IMC-DTC存在值为0.002 1的误差，而且其在上升阶段不太稳定。加入干扰信号后，IMC-DTC存在0.001 2的稳态误差。模型完全失配时仿真结果统计，如表5所示。

图9 模型完全失配时系统输出Fig.9 System output when the model is completely mismatched

表5 模型完全失配时仿真结果统计Tab.5 Statistics of simulation results when the model is completely mismatched

综上所述，可知IMC方法达到稳态值的速度较慢。而IMC-DTC无法达到设定值，均产生了误差，虽然较小，但是其上升过程中出现了超调和不稳定的情况。PID在各种情形下，其输出都出现了超调，系统产生震荡，但是在出现干扰信号后，相对来说响应较快。由于在实际生产中，不确定因素较多，所以这3种方法不太理想。相较而言，NNIMC控制方法响应速度最快，无超调，控制系统稳定，控制效果较好。