乳化沥青冷再生混合料动态模量预估模型构建

2021-02-14户桂灵韦金城韩文扬赵全满李志刚

公路工程 2021年6期

户桂灵, 韦金城, 韩文扬, 赵全满, 李志刚

(1.山东建筑大学，山东济南 250101;2.高速公路养护技术交通行业重点实验室(济南),山东济南 250031)

0 引言

近些年冷再生沥青混合料(Cold Recycling Asphalt Mixture,简称CRAM)因其寿命周期费用低、环境友好等特点得到较大规模推广应用[1-2]。CRAM主要以乳化沥青或者泡沫沥青为胶结料对路面回收料RAP(Reclaimed Asphalt Pavement)进行重新利用，并添加水泥以提高其早期强度[3-4]。CRAM在大修或重建路面结构中一般用作基层，此举也是将半刚性基层沥青路面转变为柔性基层路面的良好契机。模量是表征CRAM黏弹特性的重要指标，反映了混合料在荷载作用下的应力应变状态，同时也是路面结构设计时的输入参数，用于计算其结构层响应并预测其长期性能[5]。因此全面了解CRAM在频率、温度、胶结料含量等条件下的模量特性是非常有必要的。

国内外学者对CRAM的模量做了丰富研究。动态模量的大小与加载温度、频率、沥青含量、水泥含量、级配和养生时间有关。室内试验和数值模拟结果都显示动态模量随加载频率降低、温度增加而降低[1,6]，添加2%的水泥可以显著改善高温区动态模量稳定性[3]。而在其他条件(级配、沥青含量、水泥含量等)不变的情况下，矿粉类型对其影响并不显著[7]。有研究表明无论是室内试件还是现场试件其动态模量均随养生时间增加而增加，增加量为9%～14%不等[8]。较多研究中构建的动态模量主曲线显示CRAM具有明显的温度和频率依赖性，但与传统热拌沥青混合料(Hot Asphalt Mixture,简称HMA)相比依赖性有所降低[3,9,10]。以实测温度为输入数据分析其力学特性，结果显示CRAM动态模量的温度依赖性极大影响其力学响应变化趋势[9]。KUNA[10]等认为CRAM动态模量的频率依赖模式与HMA的并不相同，并提出了一种新的动态模量主曲线的构建方法。

在沥青路面结构设计中[11]，动态模量作为重要输入参数有3种水平，其中水平一需要实测材料在20 ℃、10 Hz时的模量，水平二需要通过将材料的基本参数输入动态模量预估模型获得，水平三则可以直接参考规范推荐值。目前虽然在研究工作中动态模量试验进行较多，但由于动态模量试验对测试人员的经验要求较高、测试设备昂贵、耗时较长等原因，在这种情况下进行结构设计时，使用动态模量预估模型是较为方便的途径。对于HMA，使用较多且效果较好的是Witzack1999模型[12]、Witzack2006模型[13]和Hirsch模型[14]，这些模型基本都以材料的基本参数(集料级配、体积参数、有效沥青含量、沥青剪切模量等)为自变量预估动态模量[15]。对于冷再生混合料的动态模量预估模型研究较少，YAN[16]对Witzack模型进行了参数修正将其用于乳化沥青冷再生混合料,YU[17]对含有少量沥青瓦(Recycling Asphalt Shingles,简称RAS)的CRAM进行动态模量预估模型修正。

综上所述，可以看出CRAM动态模量的研究基本上集中于其影响因素和利用动态模量评价CRAM性能方面，而在动态模量预估模型方面的研究则较少,这对不具备试验条件和进行低水平冷再生路面结构设计时获取动态模量较为不利。因此本文采用简单性能试验机,对不同类型的乳化沥青冷再生混合料进行系列温度频率条件下的动态模量试验，分析了影响动态模量的主要因素，借鉴前人建立热拌沥青混合料动态模量预估模型的经验，采用逐步回归分析法构建了乳化沥青冷再生混合料动态模量预估模型，为不具备试验条件或进行低水平下的沥青路面结构设计时获取动态模量数据提供了途径。

1 动态模量及其预估模型

1.1 动态模量试验和主曲线构建

动态模量试验原理为在无侧限条件下按一定温度和加载频率对试件施加轴向压应力，通过测量试件可恢复的轴向应变以获得试件动态模量[18]。沥青混合料的黏弹性质使动态模量具有时温依赖性。对不同温度和频率下测试得到的结果进行分析通常较为复杂，动态模量主曲线则提供了直观可视的结果表达。

主曲线实质是利用线性黏弹性材料的时温等效原理，即高温高频作用等同于低温低频作用，将不同温度和频率的动态模量转换为参考温度下的加载时间-动态模量曲线。同时由于仪器设备限制，较低温度域的动态模量难以通过试验得到，利用主曲线则可以对其进行估计。

AASHTO2002路面结构设计指南[19]提出利用时温等效原理，对不同温度下的动态模量进行水平平移至参考温度，使用Excel规划求解，以sigmoidal函数描述主曲线对加载频率的依赖性。

(1)

式中：|E*|为动态模量；δ为最小模量值；tr为缩减时间；δ,α为拟合系数；β，γ为描述sigmoidal函数形状的参数。tr为缩减时间，即参考温度下加载时间。

(2)

logtr=log(t)-log[a(T)]

(3)

式中：t为加载时间；a(T)为时间-温度转换系数；T为温度。

根据DONGRE[20]等采用沥青剪切动态模量试验数据得到的位移系数，同Arhennius公式既式(4)，及和VTS方法确定的位移系数具有几乎相等的数值这一结论，同时考虑参数获取的便宜性，本文位移系数计算采用Arhennius公式，通过最小二乘法构建各混合料动态模量主曲线。

log[a(T)]=1.255 88(logηT-logηTr)

(4)

式中:ηT为当前温度T和老化条件下的黏度(106Poise，1 Poise=0.1 Pa·s)；ηTr为参考温度Tr和旋转薄膜烘箱(RTFO)老化条件下的黏度(106Poise，1 Poise=0.1 Pa·s)。

1.2 动态模量预估模型

力学经验设计法将动态模量作为材料性能表征参数用来预测路面性能，而其测试方法对人员、设备和试件制作的要求均较高，实验室条件不具备条件或者进行较低等级公路的路面结构设计时，建立动态模量预估模型是较好解决问题的途径。目前研究人员针对热拌沥青混合料基于理论研究、统计回归、人工神经网络等方法建立了许多动态模量预估模型[12-14]，其中以Witczak模型[13]和Hirsch模型[14]应用最为广泛，模型分别见式(5)、式(6)、式(7)。对乳化沥青冷再生混合料动态模量预估模型的研究较少。

0.012ρ38+

(5)

(6)

(7)

式中:E*为沥青混合料动态模量(psi，1psi=6.97 kPa)；VFA为沥青填隙率,%；VMA为矿料间隙率,%。

2 试验材料及方案

本文试验选用的3种RAP回收料分别取自某高速公路A大中修项目和2条国道B、C大中修项目。回收料运送至拌合站重新破碎筛分，参考《公路沥青路面再生技术规范》JTG F41-2019[21]级配范围，根据筛分试验结果，添加不同比例新集料进行级配设计，如图1所示。选用的3种乳化沥青按照再生规范要求进行基本性能检测，均满足要求，如表1所示[22]。

图1 各试验段乳化沥青冷再生混合料级配设计

乳化沥青冷再生混合料配合比设计如表2所示，A、B、C这3种RAP料分别对应A、B、C的乳化沥青。为丰富动态模量数据，在最佳乳化沥青含量的基础上，针对每种RAP料，分别增加1种乳化沥青含量，记为A1，A2，B1，B2，C1，C2，同时为研究水泥含量对动态模量的影响，对B1另增加2种水泥含量，记为B12，B13。对不同水泥含量和乳化沥青含量的8种冷再生混合料进行动态模量试验，试验温度为5 ℃、20 ℃、35 ℃、50 ℃，频率为0.1、0.2、0.5、1、2、5、10、20、25 Hz，每种混合料进行3组平行试验，共计获得864组动态模量。

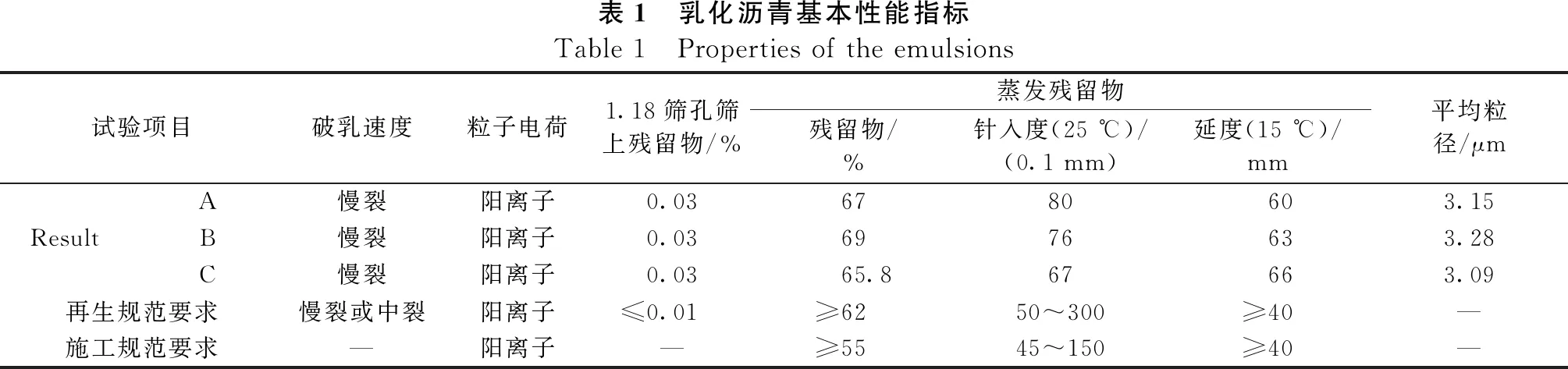
表1 乳化沥青基本性能指标Table 1 Properties of the emulsions 试验项目破乳速度粒子电荷1.18筛孔筛上残留物/%蒸发残留物残留物/%针入度(25 ℃)/(0.1 mm)延度(15 ℃)/mm平均粒径/μmA慢裂阳离子0.03 67 80 603.15ResultB慢裂阳离子0.03 69 76 633.28C慢裂阳离子0.03 65.867 663.09再生规范要求慢裂或中裂阳离子≤0.01 ≥62 50～300≥40—施工规范要求—阳离子—≥55 45～150≥40—

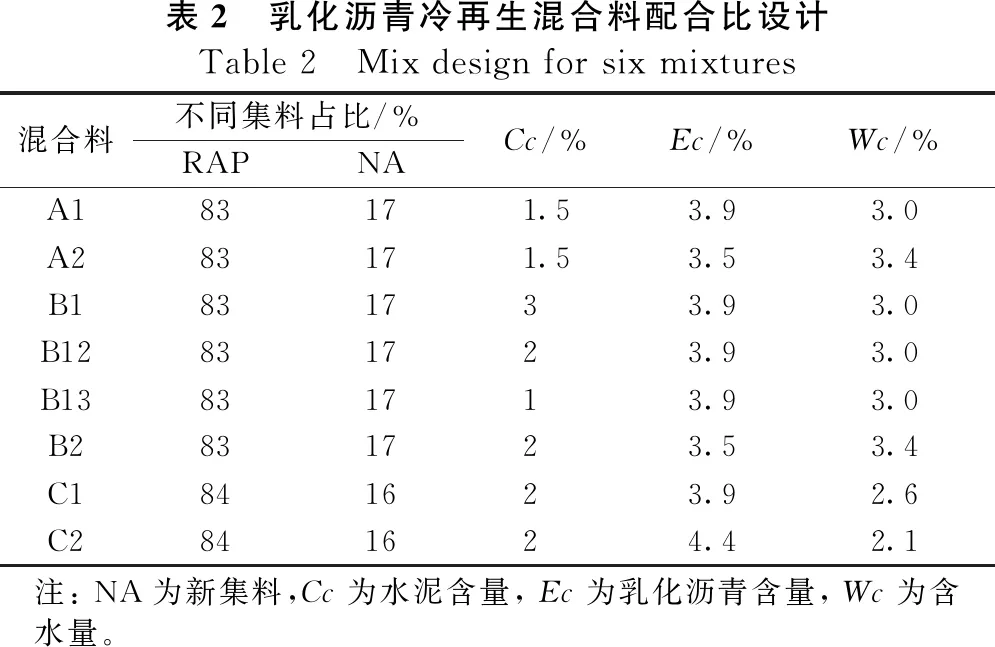
表2 乳化沥青冷再生混合料配合比设计Table 2 Mix design for six mixtures混合料不同集料占比/%RAPNACc/%Ec/%Wc/%A183171.53.93.0A283171.53.53.4B1831733.93.0B12831723.93.0B13831713.93.0B2831723.53.4C1841623.92.6C2841624.42.1注: NA为新集料,Cc为水泥含量, Ec为乳化沥青含量, Wc为含水量。

3 结果分析

3.1 变异分析

对各类型乳化沥青冷再生混合料的动态模量试验结果的变异量化分析表明：① C1和C2这2种混合料变异系数明显较其他混合料大，可能与料源本身变异性较大有关，A1在50 ℃、25 Hz时的变异系数突然降低可能与此时的动态模量升高有关，这表明变异系数与动态模量值可能存在一定关系。② 进一步探究二者关系发现，动态模量的变异系数与动态模量平均值(3组平行试件平均值)具有良好的相关关系，变异系数随动态模量降低而增大，动态模量降至2 000 MPa时，变异系数大约位于13%～24%之间，动态模量低于2 000 MPa之后，变异系数急剧增大，最大可达到42.1%，如图2所示。综合全样本数据以幂函数形式回归后相关关系良好，如图3所示。

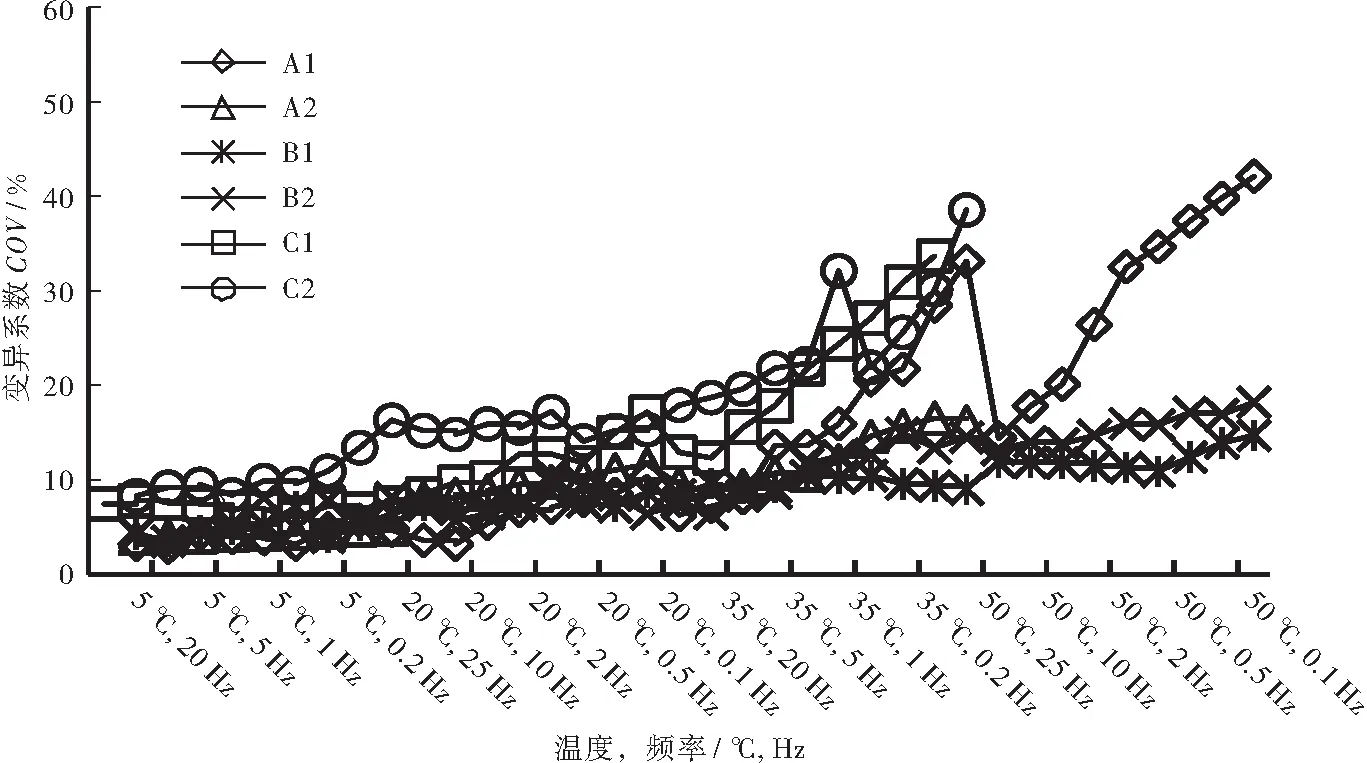
图2 不同温度频率各乳化沥青冷再生混合料变异系数

图3 变异系数与动态模量平均值

BONAQUIST[23]等在NCHRP702报告中对热拌沥青混合料动态模量变异系数与动态模量值的关系进行了针对性研究，结论认为变异系数与动态模量平均值呈幂指数形式相关关系，相关程度达到0.82，并得到按照模量平均值分类的变异系数区间，将本文变异系数与其对比发现，乳化沥青冷再生混合料动态模量的变异系数普遍大于NCHRP702报告中的值，这也间接说明乳化沥青冷再生动态模量的变异较热拌沥青混合料的变异大。

3.2 水泥含量和温度对动态模量的影响

为分析水泥含量对动态模量的影响，对国道B大中修项目中的冷再生混合料进行了3种水泥含量的动态模量试验(见图4)，图4结果表明：①水泥对中高温(20 ℃，35 ℃，50 ℃)的动态模量有明显提升作用，即提高了乳化沥青混合料中高温区的劲度水平。5 ℃时3种水泥含量下的动态模量差异并不明显。②同温度各水泥含量下频率-动态模量曲线有集中的趋势，说明水泥含量对动态模量的提升作用低频时比高频显著。③同频率下动态模量随水泥含量增大。水泥含量由1%增大至2%时动态模量提升较明显，继续增大至3%时增大趋势变缓，呈现出非线性形式。

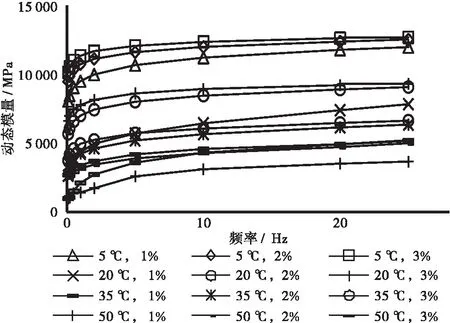
图4 不同温度频率下各水泥含量的混合料动态模量值

由于老化RAP料和水泥的存在可能会使混合料在某种程度上变“硬”，因此为分析温度和频率对混合料的动态模量是否仍然具有显著影响，在Origin统计软件中采用两因素方差分析对各类型乳化沥青冷再生混合料进行了统计检验，结果如表3所示。在显著性水平α=0.05时，动态模量各温度频率之间的差异统计显著，表明温度和频率对乳化沥青冷再生混合料的动态模量影响显著，这也说明可以将乳化沥青冷再生混合料视为黏弹性材料[3,9-10]。

3.3 动态模量主曲线

利用时温等效原理，根据动态模量试验结果，以20 ℃为参考温度对不同温度下的动态模量进行水平平移，以sigmoidal函数式(1)描述主曲线对加载频率的依赖性，使用Excel规划求解，建立8种乳化沥青冷再生混合料，并与普通热拌沥青混合料AC[24]动态模量主曲线对比，如图5所示。

表3 混合料动态模量温度频率敏感性方差分析Table 3 Two-tailed T-test statistic and corresponding P-value on dynamic modulus混合料A1A2B1B12B13B2C1C2P值温度1.39E-231.845E-208.56E-374.58E-321.50E-242.36E-331.66E-183.06E-23频率5.36E-113.46E-132.55E-222.63E-191.49E-143.57E-205.25E-102.60E-14

图5 乳化沥青冷再生混合料动态模量主曲线

由图5可以看出：

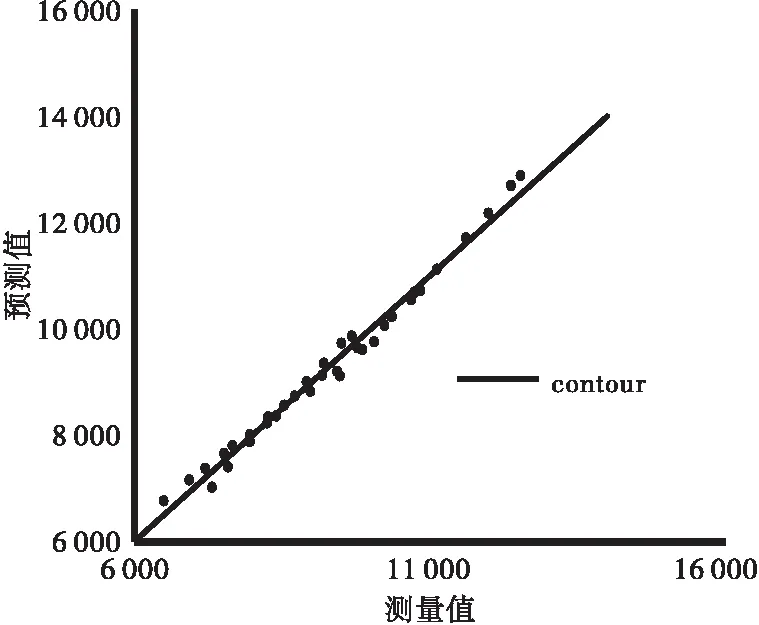
a.动态模量主曲线显示乳化沥青冷再生混合料随加载频率增大而逐渐增加，模量值均于200 MPa

b.与普通热拌沥青混合料AC20相比，如乳化沥青冷再生混合料主曲线发展趋势较平顺，表明其对加载频率的敏感性有所降低。这一趋势在中高缩减频率区域内较明显。

c.结合2.2节水泥对乳化沥青冷再生混合料动态模量的影响分析，表明低频域内乳化沥青冷再生混合料与普通热拌AC20动态模量随频率变化的趋势大体一致，但是比较其数值可以发现前者在低频(高温)的劲度仍然是显著高于后者的，水泥在相当程度上改善了高温区乳化沥青冷再生混合料的劲度水平。另外，水泥在高频(低温)区对乳化沥青冷再生劲度的提高并不明显。

3.4 Witzack模型和Hircsh模型适用性验证

图6 Witzack模型动态模量|E*|实测值与预测值(单位：MPa)

图7 Hirsch动态模量|E*|实测值与预测值(单位：MPa)

由上述预测结果与实测结果对比看出：

a.各类型热拌沥青混合料动态模量预测模型的预测值均小于实测值，对乳化沥青冷再生动态模量的预测均不理想，预测值偏离等值线较远。

b.Witzack 2006模型的预测结果表明预测值与实测值两者之间的差值先增大后减小。这可能是由于预测模型是基于热拌沥青混合料做出的，预测值的变化趋势呈现出明显的温度依赖性。水泥的加入和乳化沥青冷再生混合料中RAP料的老化使其温度敏感性较前者有较大改善，中高温区动态模量明显增大，造成两者之间变化趋势并不一致。

c.在模量值较大时，预测值和实测值比较接近，这可能是水泥对低温区(高频)的动态模量提高不再显著，以及RAP料本身强度较新集料有所衰减造成的。

d.Hirsch模型的预测值趋势与Witzack基本一致。Hirsch模型以矿料间隙率VMA和基于VMA的沥青饱和度VFA为体积特性参数，以沥青剪切模量描述沥青混合料的温度依赖性。乳化沥青冷再生沥青混合料预测中VMA的获得需要通过矿料合成毛体积密度Gsb，乳化沥青冷再生混合料的级配设计中较难实现对RAP料做密度试验，因此VMA的计算只能通过最大理论密度Gmm、沥青含量和沥青密度来推算。按照矿料合成毛体积密度计算方法，其值只与级配组成有关，可与沥青含量无关。可实际推算过程中，同一级配不同沥青含量的乳化沥青冷再生混合料矿料合成毛体积密度并不相同。这种误差进一步影响了VMA、VFA的计算，Hirsch模型中只有VMA、VFA和沥青剪切模量这3个输入参数，其中VMA与VFA输入均存在误差，使其对乳化沥青冷再生混合料动态模量的预测精确度大大降低。

4 新动态模量预估模型构建

4.1 模型参数

考虑到乳化沥青冷再生混合料的再生特性和水泥对其温度敏感性的影响，结合上一节现有热拌沥青混合料动态模量预估模型评价结果，认为对现有模型进行修正以实现乳化沥青冷再生混合料动态模量的预估难度较大，本节利用统计学原理对各基础因素和其组合因素进行多重线性回归分析，构建乳化沥青冷再生混合料动态模量预估模型。

(8)

式中:各项符号同前述公式。其中Pb为乳化沥青中基质沥青含量，通过蒸发残留物百分比得到。

4.2 预估模型

第3节试验结果分析水泥对乳化沥青冷再生混合料动态模量的影响分析显示:水泥对抑制常温和高温状态(5 ℃以上)下动态模量的衰减有显著作用，但是对低温(5 ℃)时的动态模量影响并不显著。因此对乳化沥青冷再生混合料动态模量以5 ℃为界限值，采用逐步回归分析法[24-25]分别构建预估模型。

逐步回归的基本思想是有进有出，具体做法是将前述变量单个引入，每引入一个自变量后，对已入选的变量逐个进行检验，当原引入的变量因后面变量的引入而变得不再显著时，将其剔除。引入一个变量或从回归方程中剔除一个变量为逐步回归的一步，每一步都要进行F检验，以确保每次引入新的变量之前回归方程中只包含显著的变量。反复进行此过程，直到既无显著的自变量选入回归方程，也无不显著的自变量从回归方程中剔除为止，保证最后所得回归子集是最优回归子集。

对于高温状态的动态模量，统计分析软件SPSS逐步回归共得到7个模型，按照较小平均绝对残差及较大复相关系数原则，最终得到5 ℃以上的乳化沥青冷再生混合料动态模量预估模型为：

0.468 5Wc-0.471 2Va+0.064 0P0.075-

(9)

调整后的R2=0.922。

式中:各符号意义同前。

对于低温状态(5 ℃)的动态模量，统计分析软件SPSS逐步回归共得到5个模型，按照较小平均绝对残差和较大复相关系数原则，最终得到5 ℃的乳化沥青冷再生混合料动态模量预估模型为：

0.064 5×Va-0.037 2×Vbeff+0.001 5×

(10)

调整后R2=0.984。

式中:各符号意义同前。