西部山区公路临坡桩基设计初探
2021-02-14刘家庆杨超炜
刘家庆, 杨超炜
(1.广西新发展交通集团有限公司, 广西 南宁 530028;2.湖南大学 土木工程学院, 湖南 长沙 410082)
0 引言
随着我国西部大开发战略政策的实施,西部山区的高速公路建设迅猛发展。此时,一个不可避免的问题日益突显。在我国西部,山区和丘陵地带较多,在道路选线时需要穿越崇山峻岭。同时,考虑到山区的复杂地质条件和对原始生态环境的保护,许多路线必须采用半路半桥的形式沿陡坡行进,或采用高架桥梁的形式进行整体跨越。当然,在节省土地的优势下,这些桥梁桩基将处于临坡的不利地理位置。因为相比于普通竖向受荷的桩基础,临坡段桥梁桩基的受理机制与荷载响应分析无疑要复杂得多[1-2]。而我国现行的《公路桥涵地基与基础设计规范(JTG D63—2007)》尚无相关设计计算方法[3]。
目前,临坡段桥梁桩基的设计方法大多借鉴普通平地桩基的设计方法。而在考虑到由于坡体自重、上部荷载或降水等因素可能诱导的边坡变形将使基桩不得不承受一个侧向的土压力。因此,若按普通平地桩基的设计方法进行设计将偏于不安全。早在2006年,赵明华[4]等已经提出陡坡段桥梁基桩同时兼具承重和阻滑双重功能,不仅要承受桥梁上部结构传递的复杂荷载,还要承受桩侧滑坡推力。杨明辉[5]等随后考虑了施工、暴雨、风荷载甚至地震荷载可能造成的坡体滑动,并假定桩前地基水平抗力呈线性分布。尹平保[6]等基于相似理论,进行了一系列室内模型试验,探讨了倾斜荷载下陡坡段双桩内力、位移的发展模式、不同墩柱高度、边坡坡度对双桩基础破坏模式、内力和变形的影响;试验结果表明,桩顶荷载对边坡的影响集中在2~4倍桩径范围内,且双桩-坡系统的主要破坏模式为边坡整体失稳。在此基础上,赵明华[7]等将桩身全长根据深度分为3部分:嵌固段、受荷段和自由段,并给出了对应的滑坡推力和土体抗力计算方法,计算方法通过有限杆单元法在MATLAB中实现。与此同时,张永杰[8]等提出分析坡-桩相互作用的简化模型,建议了以结构位移法为基础的陡坡段桥梁双桩基础的简化计算方法。赵明华[9]等依托湖南省张(家界)-花(垣)高速公路泗溪河一桥6#桩开展现场试验,同时提出可以分析陡坡条件下基桩内力及变形修正杆单元法;并基于该方法建立双桩基础整体受力分析模型,拟合出前桩及后桩的土压力大小和分布规律。
综上所述,国内针对临坡单桩的设计计算方法大多采用折减地基比例系数或p-y曲线等方式考虑桩前地基水平抗力。更确切地说,已有研究成果均以《公路桥涵地基基础设计规范(JTG D63—2007)》为依据对边坡土体地基比例系数进行折减。考虑到弹性地基反力法、p-y曲线的局限性,临坡桩前地基水平抗力计算仍有改进的空间。此外,还应考虑桩后土压力的影响,并提出桩后附加土压力的理论计算方法也是有必要的。因此,本文采用有限元数值计算软件ABAQUS建立临坡单桩基桩三维数值模型,并分析桩的力学和几何参数对桩身内力及边坡稳定性的影响,以期为山区公路临坡桩基设计提供一定的参考。
1 三维数值模型的定义
以湖南省某高速公路桥梁临坡桩基为例[7]。该桥梁桩基的其中一根基桩设计建造在45°的边坡之上,该桩的直径为2m,入土深度为18m,基桩由上至下分别穿越砂层、砾石层、强风化岩层,最终嵌固在稳定的微风化基岩上(嵌固深度为3.6m),桩身混凝土弹性模量为2.96×104MPa,抗弯刚度EI为2.32×107kN·m2。根据相关设计资料,基桩和其临坡的物理力学参数如表1所示。
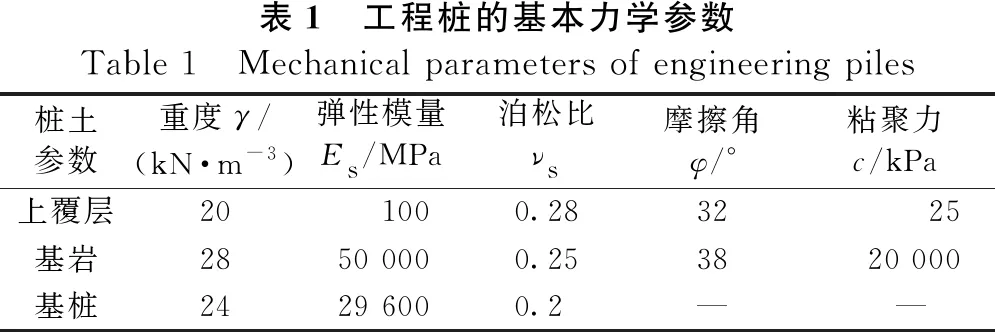
表1 工程桩的基本力学参数Table 1 Mechanical parameters of engineering piles桩土参数重度γ/(kN·m-3)弹性模量Es/MPa泊松比νs摩擦角φ/°粘聚力c/kPa上覆层201000.283225基岩2850 0000.253820 000基桩2429 6000.2——
在本文的三维数值模型中,桩周土的材料性质被假定为服从摩尔库伦破坏准则非线性理想弹塑性材料,塑性势的发展服从非关联流动法则(剪胀角ψ=0°,由于ABAQUS中剪胀角不能自行定义,可取ψ=0.1°)。此外,只考虑土体的小变形状态,可用USDFLD子程序[8]模拟模量的变化,非线性应力-应变关系如图1所示。
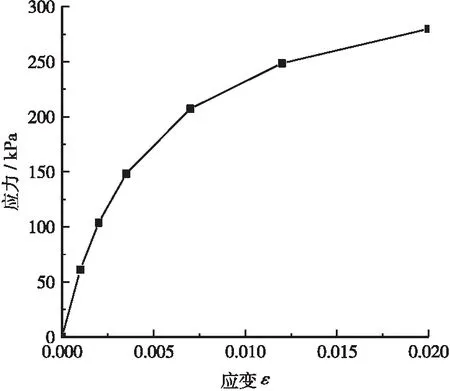
图1 基于USDFLD的非线性应力-应变曲线
三维建模过程中的土体初始应力状态设置可依据土体自重效应逐层生成。由于桩土接触单元的设置将影响模型中侧摩阻力的发挥程度,为了尽可能真实地模拟界面效应,接触单元考虑了滑动摩擦并允许滑脱[摩擦系数取tan(0.72φ)]。此外,边界条件也是模型合理性的保证。为此,模型底部为模拟完整基岩的嵌固效果,采取了零自由度完全固定的边界条件,其余4个侧面则限制与平面垂直方向上的位移(即允许2个自由度),同时坡体的位移完全不受限制。
桩顶水平荷载的施加方法采用定义桩顶单元的表面摩擦力产生。桩-土体系的网格的自动划分采用连续单元C3D8。值得注意的是,单元的密集程度决定了计算精度,因此在靠近基桩的土体生成网格需大于远离基桩的土体。具体参数如表2所示。
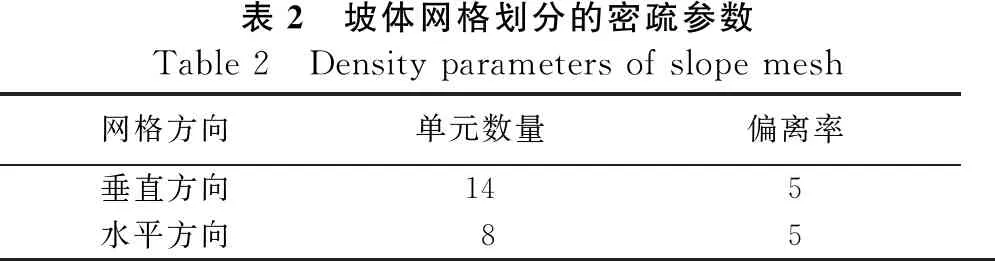
表2 坡体网格划分的密疏参数Table 2 Density parameters of slope mesh网格方向单元数量偏离率垂直方向145水平方向 85
数值模型的输入参数按表1选取。图2为模型的侧视和俯视图。自动划分的网格如图3所示。
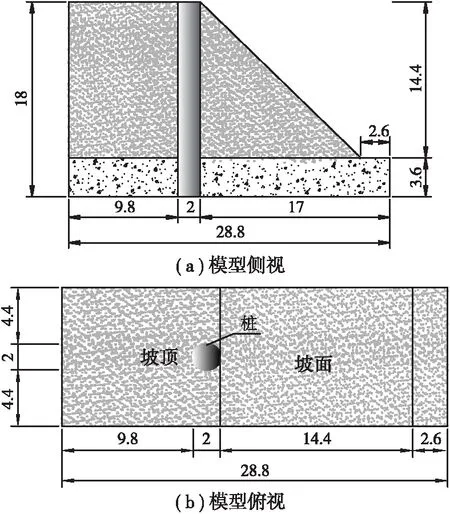
图2 三维数值模型的侧视俯视和尺寸设置(单位: m)
图3 三维数值模型的网格划分图
2 数值模型结果及参数分析
2.1 数值计算结果
图4给出了本文建立的三维数值模型的计算结果,共计算了4种不同大小的水平荷载作用在桩顶时,桩身入土深度范围内的位移变化情况。从图中可以看出,随着桩顶水平荷载的增加,桩顶位移量也随之增加,当水平荷载达到1000kN时,桩顶位移达到11mm,已经超过了现行规范的要求。这表明在实际工程中,该基桩的水平承载力特征值应小于1000kN,这与设计文件的内容是一致的。此外,随着桩顶水平荷载的增加,桩身的挠曲变形也随之增加,且12m以上土层的挠曲变形量的变化率呈非线性增加。这表明在超过一定的水平荷载值时,基桩的水平位移将随着荷载增加而大幅增加。
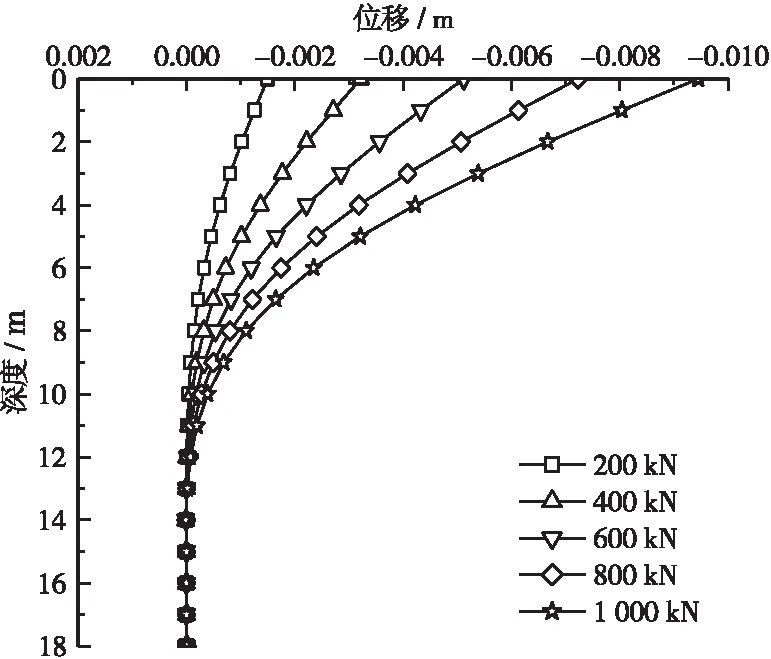
图4 不同桩顶水平荷载下的桩身挠曲变形
图5给出了本文建立的三维数值模型在水平荷载400 kN作用时的位移云图。从图中可以看出,桩身位移和坡体位移都集中发展在桩顶附近的深度内,且随着如图所示深度的增加变形量逐渐减小。
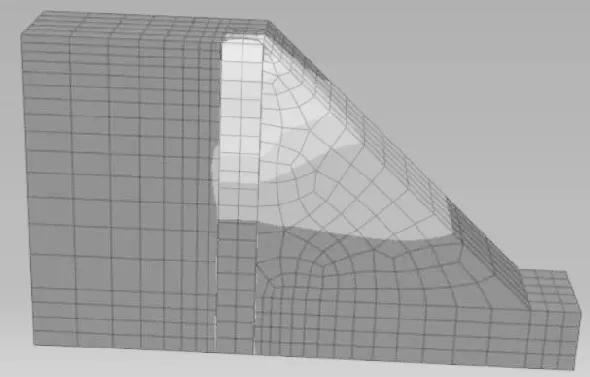
图5 水平荷载400 kN时的位移云图
2.2 与地基比例系数折减法的结果对比
弹性地基反力法是现行规范建议的水平受荷桩设计计算方法。根据入土深度与弹簧刚度的不同幂函数关系,又可分为m法、k法和C法。其中,m法是规范推荐使用的方法。但是,m法并不能考虑边坡效应对基桩水平变形的影响。为了进一步地探讨边坡对地基水平抗力的折减效应,本文选取了不折减地基比例系数和按0.5倍折减比例系数m(m′=0.5m)[10]两种理论解进行对比分析。
水平受荷单桩的挠曲四阶常微分方程如下:
(1)
式中:EI为基桩弯曲刚度;y为基桩水平位移;p(z)为深度z处的地基水平抗力,即地基比例系数m的函数,p(z)=mzy。而对于临坡水平受荷单桩,需同时考虑桩前地基水平抗力的折减和桩后的主动土压力,可将控制方程式(1)修正为:
(2)
式中:q(z)为桩后土压力,可根据文献[5]的方法计算。
图6为按m法(折减及不折减)的理论计算结果与本文数值计算结果的对比。其中,第一组y-z曲线是按照未折减的地基比例系数计算,因此并不能考虑“临坡效应”,其结果可视为普通平地桩;另外一组理论曲线是按0.5倍折减比例系数得到的;最后一组是数值计算结果。随着桩顶水平荷载的逐渐增加,桩身的挠曲变形也随之增加,理论计算方法得到的位移变化趋势与本文数值模拟结果完全一致的。
对比图6所示的3种计算方法,总结如下几点变化规律,可为临坡基桩设计提供参考。首先,假定m法计算结果为平地桩基结果,将折减地基比例系数法和数值计算法视为考虑临坡效应的两种平行对比方法。
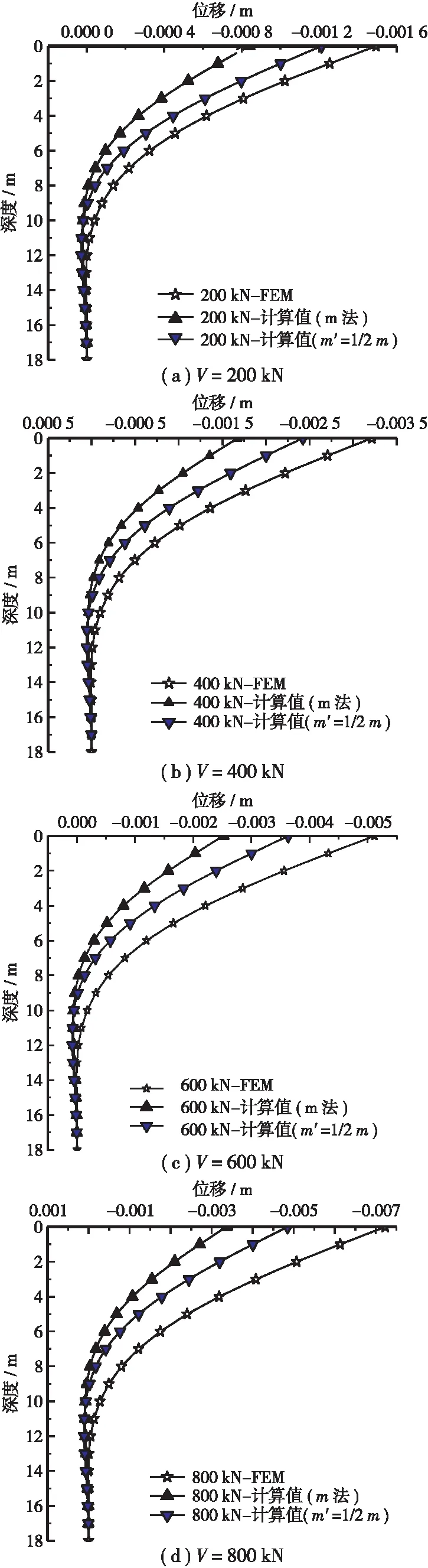
图6 理论计算结果与数值计算结果的对比
考虑临坡效应(折减地基比例系数法)时,桩顶位移随着桩顶水平荷载增加分别将提高37%、41%、45%和49%。这表明临坡效应随水平荷载的增大也越来越明显。
折减地基比例系数法的计算结果与有限元结果较为吻合,本文4个工况中最大的桩顶位移误差为27%,最小为10%。这说明折减地基比例系数法适合用于预测低水平荷载下桩顶位移,但同时可能低估高水平荷载下基桩位移。可能的解释是高水平荷载下边坡甚至难以满足自稳状态,因此计算结果将偏于不安全。显然,当设计没有条件进行有限元数值计算时,可参考折减地基比例系数法进行初步设计。
目前,除了本文所介绍的3种临坡基桩水平受荷计算方法之外,尚有弹性理论法(Mindlin法)[11]、修正应变楔模型[12]和修正p-y曲线法[13]等理论方法可以预测临坡基桩的内力和位移。限于篇幅,本文没有对这些方法进行介绍,值得一提的是,这两种方法的计算需要大量的假定和实测数据拟合,且计算过程复杂,并不利于广大工程技术人员和应用。
3 结论
由于边坡本身复杂力学性质的影响,临坡基桩的水平承载将受到坡体稳定性的制约。在这种工况下,简单地采用折减地基比例系数m来考虑边坡对地基水平抗力的弱化效应,可以近似求解基桩的水平受力变形问题。与现行规范建议的弹性反力法相比,该方法不仅考虑了土体性质沿深度的非线性变化,还能处理桩土相互作用和土的连续性。由于该方法能较为准确地反映土体的强度发挥,因此当没有条件进行有限元数值计算时,可参考折减地基比例系数法进行初步设计,尤其适合用于预测低水平荷载下桩顶位移。
