《营造法式》“上下昂理想斜率”问题析疑

喻梦哲

一、引言

“昂制”是否可以被定量地表达，是《营造法式》（以下简称《法式》）研究中的一个重要命题，笔者曾在《建筑师》撰文探讨上、下昂的“理想”斜率（参考文献[1]，以下简称《探析》），朱永春先生则从尺度分类的角度批驳了拙文观点（参考文献[2]，以下简称《解答》），认为“大木作制度中有三种尺度：固定尺度、可调尺度、构造尺度……由于可调尺度、构造尺度的存在，《法式》大木作的尺度关系，有着系统的弹性。既有研究中常不明白此理，将《法式》中有伸缩余地的尺度关系凝固化……”，试图纠正《探析》归纳不同铺数用昂“理想斜率”的“错误尝试”。

可以说，两文论争的焦点在于判断“设计”与“施工”孰为先后。斜昂倾角既反映了设计意识，也体现工法制约，更富于发抒余地（如昂头交互枓下降2～5 分°的目的到底偏倚于调试外观还是凑整构造？实效又如何？），是一个极好的讨论对象。《解答》行文犀利，意味隽永，极富启发意义，但昂身斜率固定与否事关《法式》的“示例”逻辑，更牵涉技术史研究应如何平衡图解分析与文献考据的问题，因而值得继续商榷。

二、下昂斜率是否应当被定量地观察？

面对文本中的各项数字，借由作图来推导其成立与否（或对文意的理解正确与否），是建筑学的专业本能。基于作图分析提出假设，既是对历史真实的接近，也是对构建逻辑真实的尝试，因此，关于昂身斜率的争议不宜局限在某个数值的正误上，而应以解释工匠思维为目的，《解答》正是基于这一立场向我们展示了作者深刻的思考。

该文将建筑尺度（材份的或尺寸的）定义为固定、构造与可调三种，认为后两者“表现为数值的不确定性，这是中古社会营造过程中设计与施工合一的产物。由于当时的大多数工程不同于今天的先设计后施工，今日研究者往往对此不适应，苦心为《法式》寻找‘遗漏’的材份尺度……近期喻梦哲、惠盛健撰文，为《法式》中本不存在的上、下昂斜率寻找折算方法，将上、下昂构件中可调尺度、构造尺度，凝固为固定尺度”。

对此提出两点疑问：

（1）“构造尺度”是否总是“可调”？《解答》认为“《法式》没有给出昂尾的具体长度，也没给定一可调范围，而是规定‘皆至下平槫’的构造，却不考虑昂尾的长度、斜率。又从‘或只挑一枓，或挑一材两栔’可知，昂尾的长度、斜率，都不是定值。凡《法式》中构件的某一尺度，由大木构造要求来约定，我们称构造尺度”，即给予“构造尺度”临时赋值的自由。然而，“构造尺度”需勾连特定“构造节点”方可存在，不同节点的限定条件亦宽严有别，遑论“尺度”本就不止于宏观、定性、粗略的描述（即“性质”如何），更应涉及微观、定量、精准的刻画（即“程度”如何），在某些情况下调节范围经一再缩小后，有最终凝固为定值的可能。

既然斜昂被放置于铺作材栔格网之中，它的倾斜程度理应借由其下某段三角形描述（只需确保截取的弦长对应勾、股值均能符合或接近整数份数即可）。[1]通过考察有效取值范围内是否存在契合特定构造特征的“优选值”，并论证其是否具有排他性，就有望将无限解化简为有限解甚至唯一解。为此需重点考察下平槫的“构造尺度”（参考文献[4]）：尤其需要反思基于“交互枓降2～5 分°”规定推导出的多个解值是否均能取得对应的简明构造关系。[2]

（2）官式营造中完全不存在设计环节吗？设计、施工一体化虽是常态，但因此彻底否定“方案阶段”是违背史实的。官方营建需依图施行[3]，而宋代图学、画学教育发达，（北宋）郭若虚《图画见闻志》称界画“折算无亏，笔画匀壮，深远透空，一去百斜”，意味着画师已能深刻掌握屋宇构造关系及其几何表现技法[4]，与匠师的知识、技能及职责多有重合[5]，为自营造活动中析出单独的设计环节提供了可能。南宋罢停画院，宫廷画师除少数日常留用御前外，多有散隶各处职局者，如《图绘宝鉴》记工部马和之、将作监王英孙、修内司鲁庄、甲库陈椿、车辂院刘宗古等（参考文献[5]）。他们绘制的建筑画已具有工程图学特征，当真正下至生产部门时又会有何表现？

我们在诸如日本《圆觉寺佛殿古图》（1573 年）、青海贵德万寿观砖壁明代墨绘“侧样”上仍可看见古代匠师留下的“按图施工”痕迹（图1），这些图像明确无误地展示了古代技术图纸所能达到的精度与深度，《法式》图样本身亦足资证明其再现与控制构造细节的能力。实际上，无论是如《思陵录》般列载各类构件的种属、数目与尺度，还是所谓“画宫于堵”，都需要事先明确方案，再借不同媒材传诸工匠下料、安勘。[6]否认设计环节，将设计工作笼统归结为工匠凭经验“现场放样”，是无法解释史上屡屡快速建成宫殿的事实的。大量工匠歌诀都表明了工程经验是以“常数”的方式被表记、积累和教授，若果真每逢工程皆临时量取，又谈何“匠门传承”？

图1： 古代建筑图纸举例

官方营造首重权责清晰，常依工程进度分批次绘图备查，转（参考文献[6]）摘引的几则史料如下：

（1）方案图可影响决策，如《宋会要辑稿》记“雍熙二年九月十七日，以楚王宫火，欲广宫城，诏殿前都指挥使刘延翰等经度之”并“画图来上”，后因太宗“恐动民居”而“罢之”。

（2）方案图利于决策与执行机构间的交流，并能有效约束、监察工程，如大中祥符二年诏“自今八作司凡有营造，并先定地图然后兴工，不得随时改革”，故“宋代虽无设计行业，却存在设计现象和设计阶段。”

（3）画师甚至帝王均可参与绘、改图纸，如《桯史》记开宝间赵普进呈汴京规划方案，“上览而怒，自取笔涂之，命以幅纸作大圈，纡曲纵斜，旁注云：‘依此修筑’。”

（4）建筑画可加工为方案图，如北宋刘道醇《圣朝名画评》记“太宗方营玉清宫，（吕）拙画《郁罗萧台》样上进，上览图嘉叹，下匠氏营台于宫……敕（刘）文通先立小样图，然后成葺……画毕，下匠氏为准，谓之七贤阁是也”，并评价二人“于宫殿屋木最为留意，虽匠氏亦从其法度焉。”

（5）设计工作包括多方案比较的内容，如徽宗政和四年（1114 年）“令勒都壕寨官董士 彩画到天津桥作三等样，制修砌图本一册进呈。诏依第二桥样修建。”

综上所述，《解答》关于“可调尺度、构造尺度，都有待于工匠根据经验裁定，这是中古社会设计与施工合一使然”的结论，并不能成为否定昂制之类复杂“范式”的证据。

三、下昂斜率是否应当凝固为特定取值？

《解答》在驳斥下昂“理想”斜率时，首先列出的理由即是“《法式》六铺作以上的下昂之上的坐枓，归平后要再向下2～5分°，也就是说有3分°以内的调控值。仅此而论，就不可能‘恒为’……”，这涉及对交互枓降跳规定的理解，2～5 分°的降高多被前辈学者视作《法式》灵活性的证据。问题在于：就增减昂身斜率最为直接的目的（挑斡平槫）而言，该项措施是否必要？

《法式》描述下平槫下构造的记载主要有二：（1）“若昂身于屋内上出，皆至下平槫”；（2）“若屋内彻上明造，即用挑斡。或只挑一枓，或挑一材两栔。谓一枓上下皆有枓也。”前者针对敷设天花的情形，此时昂尾插蜀柱（不限长短）挑槫，总能补足至槫下的欠高，故无需调整昂身斜率，记为定值并无不妥；后者彻上露明，“或”字连用意指构造方式“有且仅有”两种，而非可在“一枓”与“一材两栔”范围内游移，因此不能据之否定昂尾长度、斜率恒定，恰相反，该句或指“自昂尾上出”与“自挑斡上出”者各自对应一种固定斜率。

更加关键的是卷四“飞昂”条所记枓高分位的调节范围，即所谓“凡昂上坐枓，四铺作、五铺作并归平；六铺作以上，自五铺作外，昂上枓并再向下二分至五分”，到底是如何“向下”的？若昂身前后端同步下降，则降高不会导致斜率改变；若昂尾不动而令昂头绕尾端向下旋转（或昂首、尾围绕中段某点旋摆），则昂身斜势将在一定范围内增减。[7]《解答》显然持第二种观点，并举“七铺作重栱计心造、里转六铺作”为例，作图后得出“若下昂坐枓向下取5 分°，下昂的倾角约为18°，斜率比为0.325”的算值，认为《探析》“所得数据，均远超过误差的合理范围……而3/11 约0.273，（tg18°-3/11）/tg18°×100% =16%，相对误差竟达16%……”

既然两文伸张的数据是基于对交互枓降高策略的不同理解算得的，只有先确定两种方案的可行性才能裁决争议。《法式》本身并未明确定义交互枓如何“向下”，我们只能通过穷举“功效”，来尽量判断其各自合理与否。

先看“旋点法”。假设所选之点在柱缝上，六铺作在椽平长取最小值100 分°（昂尾至槫缝下）、外跳取最大值90分°（昂尖不计在内）时，可最大幅度地挑托后尾，若按18°扭转昂首，则降幅达20 分°，远超文本规定。若按《解答》配图所示，置下昂支点于里转第二跳慢栱齐心枓平外沿处，绕此点旋动昂身将使头昂下摆更远。[8]其操作步骤如下：（1）据降跳份数定交互枓外侧底角位置；（2）以旋点为中心、单材广为半径画圆；（3）自旋点连线切昂头交互枓降高后之圆弧，以量取下昂斜势变化。我们按七铺作椽平长125 分°、外跳108 分°算，昂尾仅被挑起不到1.75分°，作为一种调节手段显然收效过微[9]，不足以解决昂、槫间欠高的矛盾。据《解答》列出的最大倾角18°绘图计算[10]，七铺作只有在昂头交互枓降5 分°、同时取屋宇规模上限（十二架椽、平长125分°、槫径30 分°）的情况下，昂尾与平槫间欠高39 分°才恰可用一材两栔配替木填塞（平长增至150 分°则欠高41 分°无法填垫）；若缩小规模至六架椽、椽长100分°、槫径30 分°，则因折屋次数减少导致欠高进一步增大到43 分°（用厅堂槫径21 分°时欠高更大），可知在2～5分°范围内旋摆昂身，多数情况下并不足以弥合槫下空隙。[11]既然摆动昂身是为了微调昂尾，那么降值为何既非规整的0 或5 分°，也非随意的2～7 分°之类，而必须固定在2～5 分°这样一个貌似随机的区间内？既然按其边界值旋摆昂身也难以挑斡平槫，又为何要作此规定？若手段不足以支撑目的，我们对于手段甚至目的的理解又是否有误（图2、图3）？

图2： 七铺作下昂按“旋点法”调节效果示意

图3： 六铺作下昂按“旋点法”调节效果示意

再看“平移法”。按昂身头尾两端同步下移的方式作图，考察六铺作厅堂，若以3/8 定昂斜，只有超规模时（十架椽、平长125 分°、举高0.27[12]）才需令昂尾挑一材两栔后承直径21 分°之槫[13]；当规模趋小至正常范围内（如六架椽、平长100 分°），同样斜率的昂、槫间欠高（2分°，不足1 寸）甚至可用木楔直接垫塞。此时头昂下皮压在齐心枓口外沿处，构造关系足够简洁，挑斡平槫的目的也已达成，自然无需继续“绕点旋昂”。[14]同理，七、八铺作殿堂中，按3/11 斜率在2～5 分°范围内平移昂身，也总能在某一畸零降值上使得昂下皮与扶壁素方内（外）侧下棱重合。

此外，还可从“构造”和“形式”角度反思昂上枓降高的真实目的。

从构造合理性看，所谓的“调控弹性”应显著有利于构件制备与安勘。《法式》规定头道昂下华头子露明，是为了使之尽可能推高下昂起算分位，华头子外伸越远，就越能充分垫托昂身。若如《解答》主张的，令昂身绕点旋转，则下压昂头的同时势必截短华头子露明部分（交互枓降5 分°时华头子仅高3 分°、长5 分°，已非常局促），这反过来又限制了昂身的定高自由，岂非背离了初衷？[15]

从样式适宜性看，昂身绕点旋转的幅度有限，造成的倾角差别甚微，是否能引发立面变化尚未可知。按柱“生起”制度，殿堂逐间升高寸数似可利用昂头降值来逐铺调节，以维持檐口平直，但也只能在三间范围内生效，何况殿身内部若用平棊则无从观察昂尾细节，昂头又多为“护殿阁檐枓栱竹雀眼网”遮蔽，因此旋昂引发的外观变化极其轻微，难以察觉。

既然随宜“绕点旋昂”对于“构造”与“形式”均无积极影响，还会令昂身所过栱方全部重开榫卯，徒增烦难，那么昂头枓通过平移实现降高规定似乎更为合理，推测其目的亦非凑够槫下欠高，而是为了确保昂身过扶壁时诸多构件的交接关系趋于最简，以便于加工。

四、是否应当参鉴实例探寻昂制规律？

《解答》指出：“《探析》中下昂的‘斜率折算’方法，是将陈彤先行研究中所提出的方法，加1 分°或3 分°，简化为较为简捷的3/8、3/11 斜率比……”在撰写《探析》时，我们已详细陈述了受陈彤先生文章启发的事实（参考文献[7]、参考文献[8]），但对其“以几何约束制图确定下昂斜率”的结论提出了不同观点，认为倾斜数据同样可借由勾股比例表述，并提出了简化比值的理由：添加交互枓外鹊台后[16]，推定的下昂斜率更趋简洁（图4），且其定值模式得到了更多实例的支撑。

同样是基于弦下三角反算下昂斜率，《探析》的观察对象不再限于转角足材耍头，而是扩展至（顺直而非弯折的）昂下任意一组便于量测的勾股关系。通过举证实例，我们已抽象出一套华北宋金遗构中下昂斜率的生成“模型”（参考文献[9]），《探析》给出的推定值同样可以借由该算法转化表达，两种途径指向同一结果，因而更为可信。[17]将李诫“与诸作谙会工匠详悉讲究”后选录的“系来自工作相传、经久可以行用之法”与实例中常见的下昂斜率相互印证，正是从“一般”到“特殊”的思考过程，也是朱启钤先生提出沟通儒匠的三重手段（或三大任务）之一：“讲求李书（指《法式》）读法用法，加以演绎……举其正例变例，以为李书之羽翼（参考文献[10]）。”

《解答》进一步提出借助耍头测算昂身斜率的方法存在“问题”，认为《法式》中转角铺作耍头与用在补间者不等长，而后者长度并不固定：“五至八铺作中的里外耍头，是由一只两出耍头斜切而成。斜切的坡度与位置，取决‘昂身上下斜势’。昂尾挑斡施工过程中，昂的斜率会有微小变化。要等下昂安妥，再行切割。不难看出，耍头切割后的长、倾角，都属于构造尺度”，本文对此亦持不同看法。

按《法式》，转角诸昂中，除角缝用者外均为交角昂，从分件图看，其后尾抹斜后紧贴角内昂两侧，并不越过柱缝，自然也就较补间昂为短，但里跳构造不同未必引发外跳联动变化，更不能据此判定两者斜率各异，否则各道罗汉方与扶壁素方将高低错列，导致外观扭曲。且《法式》小字旁注称里耍头“只用单材”，无法与足材外耍头连做，并非“交斜解造”切成，其“切割后的长、倾角”自然也无需临场裁定后再行绞割。实际上，与耍头同样需“随昂身上下斜势”制备的还有头昂下“外华头子里华栱”、八铺作独用之“第四杪内华栱”等系列构件，它们的物型轮廓均需“外随昂、槫斜”，榫卯剔凿也受昂制约，若不先定斜率，此类构件是难以分别制备后统一组装的，而逐一制作必将拖慢进度，并不可行。

五、里跳上昂的功用与尺度辨疑

《解答》认为使用上昂的目的在于“提高铺作中平棊方的高度，缩短跳距，以便安置平棊”，因此无需纠结各跳间的具体份数分配。相应地，上昂斜率也主要由骑枓栱、靴楔调控（以平棊方高度而非跳距标定）。一般认为《法式》上昂主要用于槽内，向外伸出部分较为窄迫。微调上昂斜势能否达成显著增缩平棊规模的初衷？是否会使得里转过于蹇塞？这都需要作图校验。

《法式》安装平棊时似乎遵循先以薄版满铺、再用木条分隔的原则，即所谓“于背版上，四边用桯，桯内用贴，贴内留转道，缠难子，分布隔截，或长或方”，又“背版，长随间广，其广随材合缝计数，令足一架之广”，可知天花格子形态、大小不一，系经二次分割而成。既然落于平棊方上的“桯”可以随宜错动，那么改变其位置来调节天花大小，岂非比收、放上昂更加易行？

《解答》提出上昂斜率可通过增减靴楔大小或挪移骑枓栱位置来调节，作图后发现，循此思路改动多处榫卯后，所收实效仅是不超过10 分°的跳距变化[18]，对于调控平棊整体规模的目标来说可算聊胜于无。实际上，卷头造比上昂造更适于达成灵活分配跳距且按材栔关系稳步堆高铺作的目的，在实例中运用得也更广泛，两者相互替代或配合亦无不可（如苏州玄妙观三清殿中，内槽用上昂，外槽用华栱，二者总跳距近似），若非顾及形式秩序，《法式》为何要舍易求难？

关于《探析》推想的上昂斜率，《解答》提出“作图实测上昂的倾角，从五至八铺作依次为 35°、30°、21°、24°，相对误差依次为 7.14%、30.72%、15.78%、12.3 %，超过误差的合理的范围”，并将其归因于对连珠枓的两个错误假设：一是上昂下皮无需穿过枓平下沿，而是隔着靴楔，“大多情况下，上昂的下皮高于枓平，且与枓平不接触”；二是“将连珠枓高取为16 分°……有文献中的配图，均将连珠枓中的平盘枓绘成与交互枓等高，亦即 20分°。仅此，便产生20%的误差。”

《解答》认为连珠枓中的平盘枓未必高6 分°，连珠枓本身应是一个“构造尺度”，并指出《探析》按20 分°绘图，而计算时改为16 分°，以致算错。[19]实际上，“连珠”仅是描述纵向串联的排枓方式（如《汉书·律历志上》记载“日月如合璧，五星如连珠”句），而非一种具体枓型，李诫并未给出备选的枓高分配方案，枓件各部权衡都是基于耳、平、欹间固有的比例关系，因此连珠枓也只能按标准分段加和，而不能如《解答》所建议的，被视作“构造尺度”。此外，《解答》认为“昂底与枓平边缘的交接，便为一条线。使昂底与枓平都易损坏，实际上也很难办到。因此，昂底不接触枓平，隔靴楔上，是大概率的事……”，也与实际情况不符，靴楔并非华头子一般的垫块，施用目的不是将上昂自交互枓/连珠枓口内完全隔出，而是填塞两者间外端空隙，里侧仍应彼此接触。所谓上昂下皮过“连珠枓”口内沿对结构不利的说法，恐怕也与文意不合，否则又如何解释《法式》间杂用华头子与交互枓托外跳昂的规定？下昂所受檐口荷载远大于仅托平棊方之上昂，前者尚不惮自枓口内托昂，后者又何来构造安全问题？《解答》将“昂底于跳头枓口内出，其枓口外用靴楔”句中的“枓口内”释作“靴楔内伸后突出枓平里侧外沿以彻底截隔上昂与枓”的说法也难以成立，因《法式》在谈及下昂时规定“如至第二昂以上，只于枓口内出昂”，故昂身下皮过交互枓/连珠枓平外沿（而非必须经由靴楔过渡）是确凿的，上昂下皮在里侧与枓平内边沿线接触绝非偶然情形，更不会“大多情况下高于枓平，且与枓平不接触”。

《解答》认为“《法式》上昂铺作厘定的依据，并不是跳距。想从上昂跳距间的观察得到规律，当然难有所获”，将上昂跳距的意义约简为“控制平棊方总长”和“调控骑枓栱”两条，继而否定了《探析》因《法式》功限与制度章节内关于上昂各跳份数记载不一致而提出的猜想，认为两处记载章节不同，训释不能脱离语境，不应有所质疑。

事实或许并非如此。首先，认为上昂斜率不定，水平跳距也是随机取得，故无需探讨规律的观点，不能解释《探析》提出的简洁斜率恰对应简单构造的小概率现象。连珠枓有效高度16 分°，恰与某些早期遗构常用的单材广或小枓长相等，是为勾高；自昂下皮与柱缝上齐心枓交点起，算得股长28 分°，对应斜率4/7（图5）[20]。将此斜率代入《法式》所赋跳距后，发现跳头各枓间要么枓畔相对，要么间距控制在1～3 分°内，构造精微，对位齐整，应是预先设计的结果。

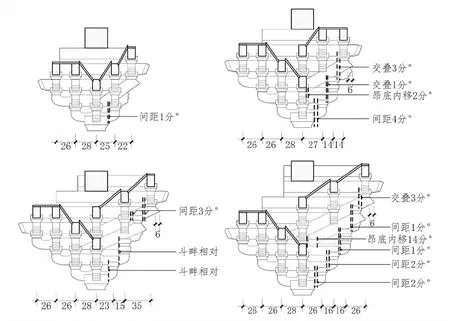
图5： 六铺作上昂固定斜率与简单构造相互耦合现象示意

至于《解答》将《法式》诸章对同一事项所列数据不同的现象释为语境不相连属的结果，更是忽视了其作为法律文本的严肃性。《宋史·刑法志》载：“禁于已然之谓敕，禁于未然之谓令，设于此以待彼之谓格，使彼效之之谓式”，撰写《法式》的根本目的即是设定“样板”以待模仿，为实际工程“比类增减”提供依据。宋神宗认为“立法足以尽事……着法者欲简于立文，详于该事。”为达成“简文”而“详事”的目的，借图样树立“范式”自然最为便捷，故而《法式》关乎丈尺、份数的举例也大多具有典型性与普适性，往往跨越章节首尾呼应，《法式》载录上昂份数不一致的现象是否仅是“语境不同”导致的，仍有待考察。

六、小结

现存唐宋遗构虽地隔辽远，昂身斜率趋同者却不在少数，且多可化简为整数比值。随机残留的实例尚能呈现规律，官颁《法式》又怎会全无安排？若对斜置构件不预加控制，又如何厘定实长留足边荒？如何有效控制斜、曲面的生成与试安装？官方营造往往多工并起，人员抽调频繁，仅靠“临时放样”又如何保障工期、避免疏漏？作为指导施工的法律文件，《法式》若不能列举“典型”，又如何“使彼效之”以关防工料？若承认其举例目的在于规范功料标准、权衡折变系数，就尤应重视对示例数值的定量分析。[21]

总言之，上、下昂斜率的数值表述，本质上是一个设计方法问题，因而假设与验证工作均应围绕不同方案能否满足预设目标展开。学者们借由图示分析反复建立、破除与重构范式（及优化其成立前提），推动着技术史研究不断深入发展，一切思考与争鸣皆服务于此目的。为此，再次感谢朱永春先生提出的宝贵批评意见，感谢匿名评审专家对于本文疏失之处的悉心指正，感谢陈斯亮老师慷慨展示所藏日本古籍以助辅证观点。

注释

[1] 对于《法式》昂制是否可如唐辽实例般以勾股比表述，存在不同观点，如陈彤在参考文献[3]中提出，《法式》五铺作下昂斜度据构造几何约束应由制图法得出，但不能合得简洁比例的份值（仅约略表示为27/71）。在参考文献[7]中进一步指出《法式》上、下昂斜度均应由几何制图获得。

[2] 《法式》侧样强调“缩尺”概念，欲厘定屋面举折必先确定铺作竖高，为使“卯眼之远近”合乎“梁柱之高下”，柱、方与平槫高度均应便于量测，昂身斜率涉及诸多卯口位置，仅靠现场放样将拉低施工效率，推测匠师应备有经过裁汰的少数几种安勘方案（使得开刻榫卯的工作尽量简便且可预估）以供参考。

[3] 如（宋）郑樵《通志·图谱略·明用》：“非图无以作宫室……为坛域者，大小高深之形，非图不能辨……为都邑者，内外轻重之势，非图不能纪……”凡欲营宫室，必先备图纸，如（宋）王应麟《玉海》：“国朝建隆三年五月，诏广皇城，命有司画洛阳宫殿，按图而修之，自是皇居壮丽矣。”

[4] 如《宣和画谱》卷八“宫室叙论”谓界画最难：“虽一点一笔，必求诸绳矩，比他画为难工，故自晋宋迄于梁隋，未闻其工者”，而“本朝郭忠恕既出，视卫贤辈其余不足数矣。”郭忠恕能“游规矩准绳之内，而不为所窘。”同时代的尹继昭亦能“作《姑苏台》《阿房宫》等……而千栋万柱，曲折广狭之制，皆有次第。又隐算学家乘除法于其间。”

[5] 如（宋）文莹《玉壶清话》记太宗“将建开宝寺塔，浙匠喻皓料一十三层，郭（忠恕）以所造小样末底一级折而计之，至上层余一尺五寸，杀收不得，谓皓曰：‘宜审之。’皓因数夕不寐，以尺较之，果如其言。”（宋）刘道醇《圣朝名画评》卷三“屋木门”称：“忠恕尤能丹青，如屋木楼观……咸取砖木诸匠本法，略不相背。”（宋）李廌《德隅斋画品》评价其所画《楼居仙图》时亦称“栋梁楹桷望之中虚，若可投足，阑楯牖户则若可以扪历而开阖之也。以毫记寸，以分记尺，以寸记丈，增而倍之，以作大宇，皆中规度，曾无少差，非至详至悉，委曲于法度之内，皆不能也。”（清）孙岳颁等修《佩文斋书画谱》卷八十二也引（明）文徵明《甫田集》：“画家宫室最难为工，须折算无差，乃为合作。盖束于绳矩笔墨，不可以逞。稍涉畦畛，便入庸匠。”可知画师需明晰宫室、津桥、舟车等工程之“法度”，并具备比例、投影等数学知识。

[6] 匠师借图、样阐释方案的事例不胜枚举。如《晋书》记武帝“尝问汉宫室制度及建章千门万户”，张华“画地为图，左右属目，帝甚异之”，王应麟认为“张华固博物矣，此博物之效也，见汉室宫室图焉”（《玉海·图谱略·原学》）；《魏书》记蒋少游“从于平城，将营太庙、太极殿，遣少游乘传诣洛，量准魏、晋基址……少游又为太极立模范”，即测绘遗址、制作模型；隋唐之际，匠师、画师身份多有重叠，如《历代名画记》称“国初二阎擅美匠学，杨、展精意宫观”，至柳宗元撰《梓人传》，都料匠“画宫于堵而绩于成……善运众工而不伐艺”，脑体分工已然完成；唐末韩偓撰《迷楼记》称隋炀帝“诏而问之，（项）升曰：‘臣先进图本。’后进数图，帝览大悦……”，即图纸分套，各有侧重，此事即或出于杜撰，也可旁窥唐末营造程序之一斑。

[7] 两种操作手段一般被归纳为“平移法”和“旋点法”，前者出自《〈营造法式〉注释》，后者出自参考文献[7]。

[8] 下平槫标高既然属于“构造尺度”，自应联动于椽架规模及椽长、跳距分配，但按0.325的斜率（约略对应于18°）绘图后发现昂尾未能抵达下平槫缝，这在构造上是不可能的。

[9] 下摆（5-2）分°×[（125-54+8）/（54-8+82+6）]分°=1.7687，《解答》令交互枓坐在昂上皮处，下摆后外端结束于交互枓底外侧，故需另加半个枓长8分°。

[10] 《解答》图1实际绘制了昂首降2分°的情形（下昂斜角18.54°），降5分°时应为19.69°，归平时17.71°。

[11] 需要说明的是，以上数值仅是针对“旋点”原则作出的理论推演，陈彤先生撰写参考文献[3]时，仍是基于故宫本图样中“八架椽屋乳栿对六椽栿用三柱”昂上枓向下4分°、昂尾挑一材两栔、中段支于补间壁内慢栱齐心枓外棱的事实，推测头昂上枓降高的目的在于调节厅堂铺作下昂斜度，使之满足彻上明造室内“或只挑一枓，或挑一材两栔”二者择一的构造要求；至于殿堂头昂上枓，则未必与厅堂做法趋同。

[12] 既有研究常认为梁思成先生给定的屋架坡度过于平缓，会导致梁背穿透屋面，这或许是对月梁制度的不同理解造成的——同等规模下，厅堂梁栿的有效高度可依准直梁高即36分°，月梁超出此数的部分并非结构必需，应是缴贴令大的结果（若给定的50～60分°高度全属密实，又何须再设缴背？），因此保障42分°的实高已经足够，其上拼贴部分完全可以放过椽身，自然无碍安勘。

[13] 若采用参考文献[8]建议的屋架坡度即0.33举，则配以直径30 分°之殿阁用槫时亦可与3/8斜率契合。

[14] 当椽长125分°、交互枓下降2分°时，昂尾抬升2×（125+8）/（60-8+6）=4.6分°，此时槫径按18分°计，将昂首降低1分°即可弥补昂、槫间3分°欠高；同理，当交互枓下降5分°时，昂尾抬高5×（125+8）/（60-8+6）=11.5分°，仍小于一材一栔，无法“只挑一枓”，椽长100分°时情况与之类似。故推测2～5分°的降高设定并不关涉昂尾挑斡平槫的构造需求。

[15] 唐辽时下昂自交互枓口内伸出，《法式》则规定下道昂以华头子伸出承托，其上各道昂仍由枓口内出。文献[2]指出：“梁先生所绘七、八铺作的昂上斗向下4分°，将其下的华头子压缩得甚短，斗口外长度显然不足9分°”，即认为“平移法”也存在类似问题。

[16] 《法式》交互枓与平盘枓底均开豁口，若其端头与昂嘴边缘齐平，则枓下开槽尽处亦应与枓底外棱重合，但图样中特意留出一段空白，此细节应不是翻刻或疏漏所致。另，图内小字旁注“昂上用”且刻意绘出枓底榫卯细节，如非构造特殊，又何须专门“别立图样”？同图中的合角下昂分件也作类似描绘，设若交互枓底与昂上皮重合，则昂嘴两侧弧棱也应始自此处，即与昂上楔状“鼻子”前缘共线，但图中所有昂嘴边棱均在“鼻子”之外。综上，《探析》将此部分计入鹊台1～3分°后代入昂斜运算过程，并非为了刻意凑整，“化简”斜率是自然结果而非预设目标。需要指出的是，对此推想亦存在不同观点，如陈彤先生即援引故宫本《法式》图样，认为交互枓外不设鹊台。

[17] 自实例总结的计算模型为：以材广为勾高、以标准跳距（两材广）为股长定三角形，维持勾高不变，以材广、厚之公因数5分°为基准量A，以若干个A为单元拉伸股长，形成所需斜率。五六铺作和七八铺作的昂斜按此算式可表示为15/（30+5+5）=3/8和15/（30+5+5+5+5+5）=3/11；若按实际构造，则可替换为（21+6）/65+6+1=3/8和（21+6）/90+6+3=3/11，取值相同。

[18] 五铺作无骑枓栱，仅靠靴楔调节，极限状态为里跳令栱内缘与第一杪端头列作一线，跳距（22分°）除去两个“半枓”长后仅剩6 分°；六铺作极限状态下令栱与连珠枓边缘对缝，可调值12分°（作图为13分°，留1分°以防齐心枓相犯）；七铺作出上昂两根，无论如何转动里跳令栱皆不能与连珠枓重合，两齐心枓畔相对时可调值为35-18=17分°，但头道昂上枓夹在其间，分之为两跳，实际可调值仅9 分°；八铺作若使里跳令栱与连珠枓重合，则头昂上枓应缩在连珠枓缝之内（或与其共缝），若上述诸枓皆在跳中，则可调值为10分°（总跳距26 分°减去两个“半枓”16 分°）。

[19] 无论上层枓是否保留枓耳，有效高度都只有6 分°，下层枓则是实木块隐出耳、平、欹分体线做成，仍按10分°定高，故《探析》按枓高16 分°计算。另蒙朱永春先生惠示，知《探析》因疏忽导致错标图名，但对于“五铺作上昂中，不存在连珠枓。‘连珠枓高’何从谈起？”的质询则要稍加解释：既然连珠枓在六至八铺作中普遍存在，能否借其“概念”量度包括五铺作在内的各级上昂勾股呢？此系主观推想，并非笔误所致。

[20] 回顾《解析》提出的上昂“理想”斜率，的确存在过度追求数值递变形式的问题，推算的六铺作上昂下三角形股长过长，导致昂势过缓（4/10），作为斜撑并不合宜，其后尾托令栱处的节点设计亦不甚妥帖。若将昂下皮与扶壁栱交点选在齐心枓底内棱处，则斜率改为4/7，数比同样简洁，且按此斜率，七铺作时昂下皮与扶壁栱交点移至齐心枓底外棱，同样便于记忆。

[21] 《法式》的一大特点就是兼顾原则性与灵活性，为便于实施而在坚持标准的同时赋予不同事项相对弹性，但这与它建立“规范”的初衷并不矛盾，即允许灵活而崇尚标准。