基于2维信息传递的wBRB多元LDPC译码算法

杜立婵，韦冬雪，黎相成，陈海强，覃团发*

(1.南宁职业技术学院 人工智能学院， 广西 南宁 530008；2.广西大学 计算机与电子信息学院， 广西 南宁 530004；3.广西多媒体通信与网络技术重点实验室， 广西 南宁 530004)

0 引言

多元低密度奇偶校验码(low-density parity-check, LDPC)具有比二进制LDPC码更优的译码性能，特别对于中短码长，其优势更明显[1-5]。此外，由于多元LDPC码的天然属性，非常适合与高阶调制技术相结合，以及具有较强的纠正突发错误能力。多元LDPC码的这些技术特点正好迎合了未来无线通信技术对低能耗、高频谱效率及高可靠性等方面的要求。然而，相比二进制LDPC码译码算法，多元LDPC码的译码复杂度和对存储空间的需求是非常高的，特别是置信传播译码算法[1]，其应用场景受到较大限制。例如，研究人员针对多元LDPC码提出了多元和积译码算法(Q-ary sum-product algorithm, QSPA)[6-7]，该算法基于置信传播的思想，获得了优异的译码性能。然而，由于QSPA译码算法是基于概率域译码，需反复进行复杂的浮点数运算，其复杂度是非常高的。为使QSPA算法获得实际应用，文献[1]把快速傅立叶变换(fast fourier transform, FFT)引入到译码算法中，提出了一种FFT-QSPA译码算法，相比基于可靠度的译码算法，此类译码算法复杂度仍然是比较高的。为了进一步降低上述BP类译码算法的复杂度，文献[8-10]提出了一种低复杂度扩展最小和(extend min-sum, EMS)多元LDPC译码算法，该算法是基于二元LDPC码的最小和(Min-Sum)算法提出的。其后，基于EMS多元LDPC译码算法，研究者提出了基于Trellis的EMS(T-EMS)[11-12]以及Min-Max译码算法[13-14]。当然，随着复杂度的降低，其译码性能也下降了。由LIN等首先提出的一类基于可靠度的迭代大数逻辑译码算法[15-18]，该类算法复杂度低，但对于列重较小的多元LDPC码存在明显地错误平层。因此，许多研究者一直致力于研究译码性能较好且复杂度较低的译码算法。近年来，研究者提出的基于可靠度的译码方案因其把信道信息量化为整数进行译码运算，复杂度大为降低。特别是针对多元LDPC码提出的基于比特可靠度的算法，因其在译码复杂度较低的情况下，仍能获得不错的译码性能，是最近几年的一个热点研究方向。

最近，HUANG等[19]在多元LDPC译码算法中，引入了按比特可靠度进行译码信息更新的大数逻辑多元LDPC译码算法(BRB-MLGD，bit-reliability based-majority logic decoding，简称BRB，其中，wBRB是其加权版本)，有别于其他多元LDPC译码算法在信息处理时按符号进行处理，wBRB算法的信息处理和更新是按比特进行的。wBRB译码算法在校验点采用Min-Sum原理按比特获取软信息，在变量节点对外信息采用基于汉明距离的系数进行修正。相比其他基于符号可靠度的译码算法，wBRB算法在保持较好译码性能的同时，其计算复杂度更低，存储负荷更小。该算法在校验节点的计算复杂度可以降为O(logq)，其译码性能与BP类译码算法可以缩小至1 dB以内。然而，wBRB算法在信息更新过程中还是存在明显的性能损失。首先wBRB算法只采用最小比特可靠度作为整个符号的可靠度，会存在域q越大，译码信息损失越严重；此外，在变量节点，只传递1维最大可靠度的符号信息，也会存在明显的译码性能损失，因为在校验不通过时，次大可靠度符号也极有可能是正确的译码符号。因此，wBRB算法在高阶域的或低列重的情况下，会存在明显的译码性能下降。

在上述基于BRB类多元LDPC译码算法基础上，为获得更优的纠错性能，本文提出了一种基于符号可靠度距离的2维信息传递wBRB多元LDPC译码算法。该算法通过引入MP类算法的思想，针对变量节点与校验节点之间的信息更新机制，在变量节点，采用2维信息进行译码信息传递，该信息由两个最有可能的有限域符号及对应的可靠度值构成。此外，在校验节点，通过计算2个最有价值的外信息符号及其可靠度，实现高效可靠的译码信息传递。通过仿真实验表明，本文提出的算法相比文献[19]提出的原版wBRB算法，大约能获得0.2～0.3 dB的译码性能增益。

1 系统模型及相关定义

2 wBRB译码算法回顾

经典的多元LDPC译码算法在译码迭代时，基本都是对有限域符号进行相关迭代信息处理，而文献[19]提出的基于比特可靠度的多元LDPC译码算法(BRB)，则是采用对符号相应的二进制比特信息进行迭代更新处理，取代原来基于有限域元素符号信息的更新方法。为便于对本文算法的描述，首先对wBRB算法进行简要描述。

① 相关信息初始化

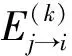
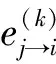
② 校验节点信息处理

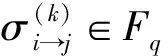
(2)

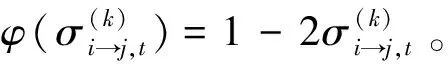
③ 变量节点信息处理

上述式(3)已计算获得来自校验节点的外信息符号对应的比特可靠度软信息，在变量节点对来自与其相连接的校验节点外可靠度软信息进行加权处理，具体实现方法如式(4)所示：

(4)

式中，0≤j≤n-1和0≤t≤l-1,θ为修正系数向量，其长度为

同时，对第j个变量节点符号按比特可靠度方式进行信息的更新，其方法如式(5)所示：

(5)

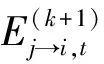
(6)

式中，0≤j≤n-1和0≤t≤l-1。

特别说明，在上述式(4)中，如果向量θ中的每个元素均设置为1，即等价于没有引入加权系数，则该译码算法就为原始的BRB算法；如根据汉明距离设置不同的权重，则为加权的wBRB译码算法，wBRB算法的译码性能明显优于BRB算法。

3 本文算法描述

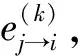
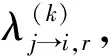
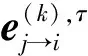
其对应的可靠度信息计算方法如式(9)所示：

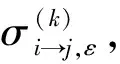
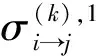
3.1 校验节点2维信息处理方法

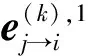
相应的，其符号可靠度信息计算方法如式(11)所示：

第二组外信息集合由两个下标子集J1和J2构成，基于两个外信息符号可靠度值之间的距离特征，对与之相邻的变量节点进行分类，下标子集J1和J2的定义如式(12)和(13)所示：

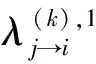
相应的，其符号可靠度信息可采用Min-Sum算法原理计算，具体计算方法如式(15)所示。

3.2 变量节点2维信息处理

式中，

接下来的实现步骤与wBRB译码算法相同。为完整、清晰的描述所提算法的实现过程，详细步骤描述如下：

Step 1:输入

初始信道信息向量y=(y0,y1,…,yn-1),量化处理比特位数b,量化间隔Δ以及设置最大迭代次数Imax。

Step 2:初始化

① 对向量yj按比特进行均匀量化处理，获得整数向量qj；

② 设置循环迭代次数控制变量k=0,加权系数向量θw,这里w=1，2；

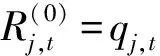
Step 3:译码迭代过程

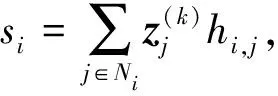
② 当k>=Imax时，退出迭代过程，返回译码失败；

③ 对0≤i≤m-1,0≤t≤l-1和j∈Ni,在校验节点，基于变量节点传递来的2维信息，按式(10)、(11)、(14)和(15)计算外信息符号及其相应的可靠度信息；

④ 对0≤j≤n-1和0≤t≤l-1,在变量节点，对外信息采用基于汉明距离的修正系数按式(16)和(5)进行加权处理；

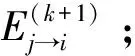
⑥ 设置k=k+1。

Step 4:输出

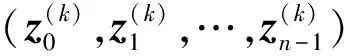
4 算法复杂度及实验仿真分析

4.1 复杂度分析

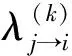
表1 单次译码迭代计算复杂度比较表Tab.1 Number of operations per iteration

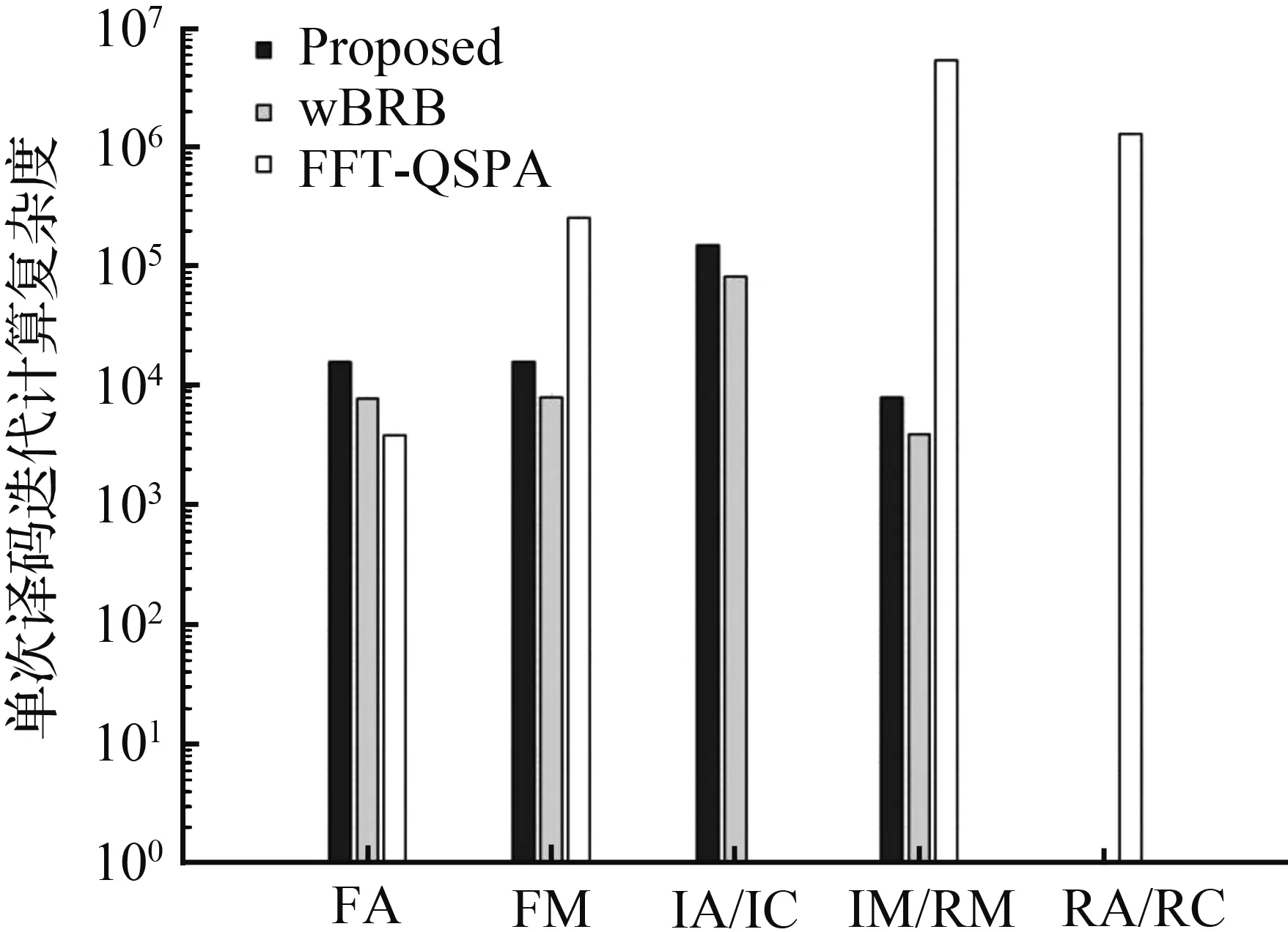
图1 F32上(1 000,900)多元LDPC码单次译码迭代计算复杂度Fig.1 Number of operations per iteration for the (1000,900) nonbinary LDPC code over F32

4.2 实验仿真分析

实验1：为对本文提出的译码算法性能进行验证和比较，仿真实验选择对F8(6 000,5 700)多元规则QC-LDPC码，其码率为0.95，列重为3，行重为60。本文及wBRB算法均采用12-bit均匀量化方案，量化间隔为0.003 9。最大译码迭代次数设置为Imax=50次；对wBRB算法，按文献[19]，设置θ=(1.60,1.20,0.20)；对本文算法设置为：d=75,θ1=(0.15,0.10,0.01,0.01)和θ2=(0.08,0.06,0.002,0.002)。由上述设置的系数向量可以看出，本文算法由于采用了2维译码信息的传递，且传递的是符号可靠度信息，而wBRB算法采用数值较小的比特可靠度，因此，其修正系数的数值明显比wBRB算法中的向量数值小。其译码性能如图2所示。

从图2可以看出：①本文提出的基于2维信息传递的wBRB译码算法，其性能与wBRB译码算法相比，在BER为10-4时，本文算法大约能获得0.2 dB性能增益；②与性能最优复杂度最高的FFT-QSPA译码算法相比，在BER为10-4时，本文算法与其存在0.28 dB左右的性能差距。

实验2：选择对F32(1 000,900)多元LDPC规则码进行仿真实验，该多元LDPC码的码率为0.90，列重为4，行重为40。本文及wBRB算法均采用12-bit均匀量化方案，量化间隔为0.003 9。最大译码迭代次数设置为Imax=50次；对wBRB算法，按文献[19]，设置θ=(2.50,2.00,0.25)；对本文算法设置为：d=200,θ1=(0.1,0.08,0.015,0.005,0.002)和θ2=(0.045,0.035,0.006,0.003,0.001)。其译码性能如图3所示。

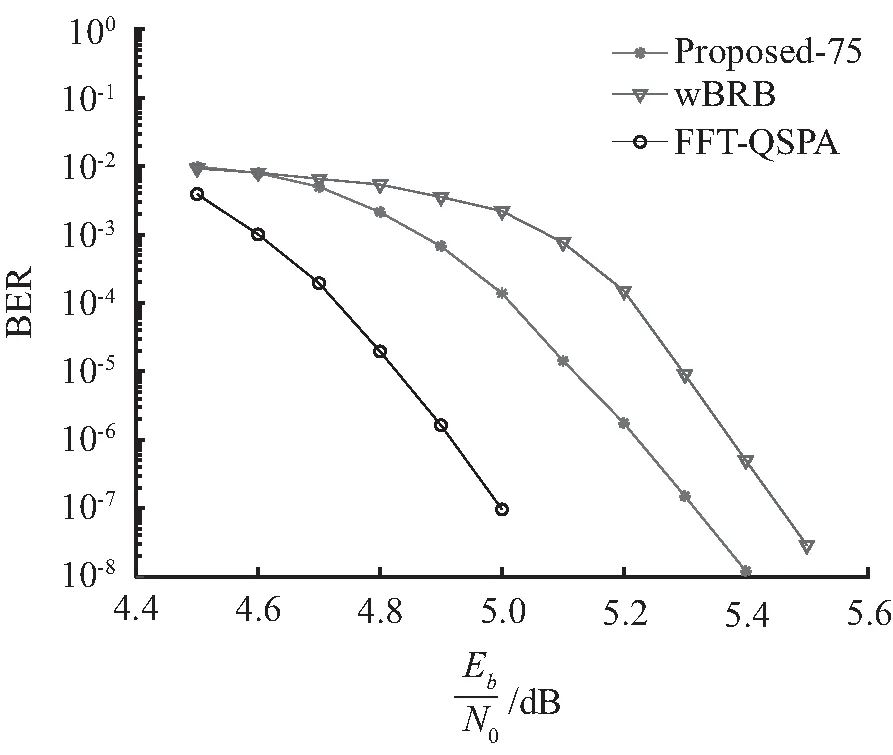
图2 F8上(6 000,5 700)多元LDPC码译码性能比较Fig.2 Error performances of the(6 000,5 700) nonbinary LDPC code over F8

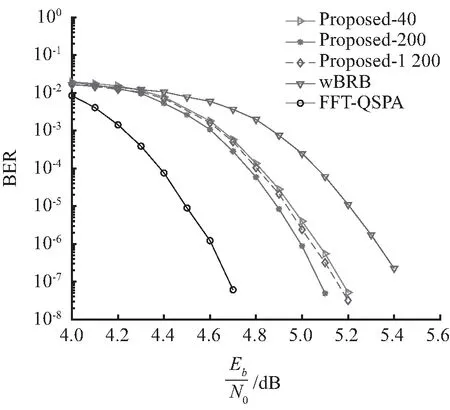
图3 F32上(1 000,900)多元LDPC码译码性能比较Fig.3 Error performances of the (1 000,900) nonbinary LDPC code over F32

从图3可以看出：①本文提出的基于2维信息传递的wBRB译码算法，其性能与wBRB译码算法相比，在BER为10-4时，本文算法大约能获得0.3 dB性能增益；②与性能最优复杂度最高的FFT-QSPA译码算法相比，在BER为10-4时，本文算法与其存在0.37 dB左右的性能差距。

5 结语

本文提出了一种基于2维译码信息传递的wBRB多元LDPC译码算法，该算法基于MP类算法思想，在变量和校验节点采用2维信息处理策略，利用符号可靠度进行信息传递，实现了更全面更有效的译码信息处理方法。本算法利用符号可靠度之间的距离信息作为度量，合理地把2维信息划分为最可靠和次可靠的两组译码信息集合，基于该信息集合，在校验节点仅计算两个最有价值的外信息符号及其可靠度。相比其他同类算法，本文算法设计了更优的译码信息获取和更新策略，实现译码性能的提升。最后，通过算法复杂度分析和仿真实验结果表明，与原版wBRB算法相比，本文提出的译码算法大约能获得0.2～0.3 dB的译码性能增益，在译码性能和复杂度之间取得较好的平衡。