基于激光干涉法的CO2气体压力测量
2021-02-11张博涵杨军谢兴娟张大治姜延欢
张博涵,杨军,谢兴娟,张大治,姜延欢
(航空工业北京长城计量测试技术研究所,北京 100095)
0 引言
目前压力测量的主要方法是依靠传统的压力传感器进行检测,虽然测量精度高,成本低,但是也存在因重复性和长时性工作所产生的磨损、测量准确度下降、失常校准、无法溯源等问题。为解决这些问题,许多国家的计量技术研究机构不断地探索如何将激光技术应用于压力测量和校准领域中[1-4]。其中,德国联邦技术物理研究所(PTB)设计了一种基于折射率的水脉冲压力激光干涉测量方法[5];北京长城计量测试技术研究所进行了基于激光干涉法的液体脉冲压力校准和正弦压力校准研究等[6-7];而针对气体介质,中国科学技术大学的许玉蓉[8]等人设计了一种法布里-珀罗腔的氩气折射率精密测量方法,并建立了气体静态压力和折射率的关系;四川大学的邓博文[9]等人利用迈克尔逊干涉仪原理,通过静压下的干涉条纹得到气体压强和折射率之间的关系;美国国家标准与技术研究院(NIST)也在计划通过激光干涉法来实现气体压力和温度的测量[11]。本文针对气体压力测量中的溯源问题,通过理论分析,建立了基于光程变化的气体压力测量模型,并通过实验进行验证。
1 气体压力测量原理
根据克劳修斯-莫索提(Clausius-Mossotti)方程[12]和洛伦兹-洛伦茨(Lorentz-Lorenz)方程[13]可知,对非极性、且均匀的气体介质,有
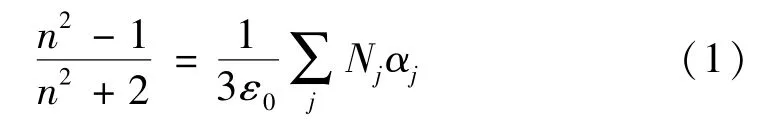
式中:n为气体折射率;ε0为真空介电常数,F/m;Nj为单位体积内的j分子的分子数;αj为分子极化率,(C·m2)/V。单位体积内的分子数Nj又可表达为

式中:ρj为气体j的密度,g/cm3;Mmol-j为摩尔质量,g/mol;NA为阿伏伽德罗常数,mol-1。
式(1)可表达为

根据热力学原理,从理想气体状态方程[14]角度考虑,消去介质密度ρ,可得理想气体平衡状态条件下,气体压力与折射率的关系为

式中:pj为气体j的压强,Pa;R为理想气体常数,J/(mol·K);T为温度,K。
气体折射率的测量,通常利用激光干涉技术测量气体介质因压力变化导致的光程差值的方式来实现,其折射率-光程差关系为

式中:Δl为光程差,cm;Δn为折射率差;L为物理光程,cm。
在以真空状态折射率为1的情况下,基于激光干涉技术测量气体的折射率n为1+Δn,以某种气体为研究对象时,式(4)可表达为

式(6)建立了气体压力与光程的关系,这样就可以将气体压力值追溯到光程变化量上。
2 气体压力测量实验
气体压力测量装置如图1所示,主要由高精度压力控制器、激光干涉仪、真空泵、变温压力气室和计算机系统组成。
在实验过程中,先利用真空泵对气室抽真空,然后通过压力控制器控制气室内的压强,根据压力控制器的量程条件设定其压力变化范围为0.1~0.3 MPa,考虑实际光程变化量很小和更好地展现光程差-压力关系等因素,选择步进量为0.05 MPa。通过气室的温度控制功能改变气室温度,考虑密闭气室温度控制单元的局限性和高温下的不稳定性,选择设定气室内温度为293,313,333 K三个温度点。采用德国SIOS SP2000-DI型激光干涉仪搭配用户软件,采集气室内压力、温度变化过程中的光程改变量。
3 实验结果
3.1 光程差测量结果
在293,313,333 K温度下,压力分别为0.1,0.15,0.2,0.25,0.3 MPa的光程差测量结果如图2所示。
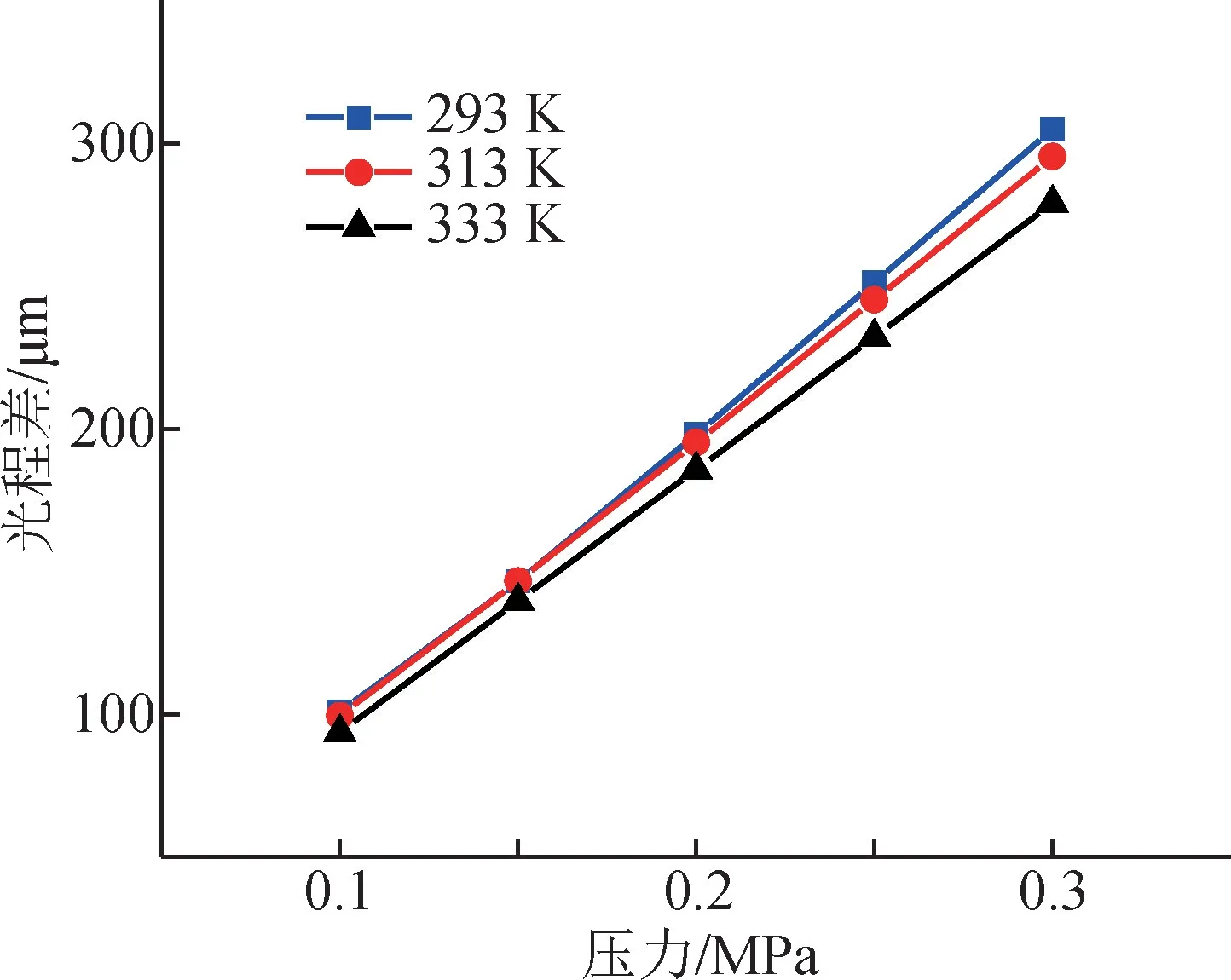
图2 光程差测量结果图Fig.2 Optical path difference measurement result graph
图2中光程差的测量是以真空为基准,通过充入高纯CO2气体改变压力而测得的光程变化量。且在每个采集点分别进行了20次采样,取其平均值作为光程差数据。可知:在0.1~0.3 MPa压力范围内,光程差和压力呈良好的线性关系,其线性值可用光程差测量灵敏度进行表示。
在本文中定义光程差变化量与压力变化量的比值作为光程差测量灵敏度s,即

根据实验计算得到293,313,333 K温度条件下光程差测量灵敏度值分别为102.60,98.09,92.66。可见随着温度的升高,灵敏度值减小,同等压力变化量引起的光程差变化减小,气体折射率也呈下降的趋势,与式(4)中温度和折射率的关系相符。
3.2 压力计算结果
在本次实验中,采用的是高纯CO2气体,假设其分子极化率在实验温度下受温度影响比较微弱,可视为常量,将光程差数据代入式(6),可计算得到压力值,结果如图3所示。

图3 不同温度条件下,压力计算结果图Fig.3 Diagram of pressure calculation results under different temperature conditions
由图3可以看出,在室温(293 K)条件下,压力测量结果绝对误差较小,在0.15 MPa压力点的测量相对误差达到最大(为3.02%),在0.1 MPa压力点的测量相对误差最小(约为0.04%),平均相对误差为1.25%;而当温度升高后,压力测量误差变大,绝对误差随着压力增大呈现上升趋势,在313 K条件下,压力测量结果相对误差在3.00%~5.00%,在333 K条件下,压力测量结果相对误差在4.00%~5.00%。
根据不同温度下的压力测量结果与参考压力的对比,分析误差主要来源包括以下几个方面:第一,压力理论模型的建立采用的是理想状态下的经验方程,且对相对磁导率和分子极化率等参数进行了简化,从而产生理论误差;第二,实验装置本身设计存在局限性,其温度测量点只有一个,导致实验过程中进行升温操作时气室内的温度测量不够精准;第三,在实际光程差数据测量过程中,吸收池无法达到绝对真空状态,影响折射率的测量结果。
4 结论
根据有关折射率的洛伦兹-洛伦茨方程和气体状态方程,推导并建立了一种基于光程变化的气体压力测量模型,并进行了实验验证。实验结果表明:在室温条件下,基于激光干涉法的气体压力测量准确度较高,平均相对误差为1.25%,验证了理论模型的正确性。此次气体压力测量研究工作可为动态压力测量和压力校准技术提供参考。针对实验过程中温度升高使测量误差变大的情况,将在后续工作中继续进行探索。
