四柱式力传感器固有频率提升研究

吕浩然,赵印明,王敏宁,黎永前

(1.航空工业北京长城计量测试技术研究所,北京 100095；2.西北工业大学空天微纳系统教育部重点实验室,陕西 西安 710072）

0 引言

目前,应用于工程的传感器主要有电阻应变式传感器、压电式力传感器和压阻式力传感器。电阻应变式传感器之中的四柱式电阻应变式力传感器因测量原理的不同,相较其它力学传感器具有优越的静态性能,但动态性能较差。研究与提升四柱式电阻应变式力传感器的动态性能成为其发展与应用中的关键技术问题。

国外对于力传感器动态特性的研究多集中于惯性补偿和滤波消噪方面[1-8],国内则集中在动态测试中的噪声处理、传感器的动态补偿和解耦方面[9-14],力传感器自身结构对固有频率的影响以及改进方法还未形成系统性的研究,四柱式传感器作为一种新式结构的力传感器,相关研究则更少。传感器最重要的动态特性指标是固有频率,它是研究与优化其他动态性能参数的基础。本文对四柱式传感器固有频率进行研究与优化,开展四柱式传感器的固有频率与结构参数的关系分析与研究,提升应变式传感器固有频率,进而提升传感器的动态性能。

1 固有频率理论研究

1.1 固有频率理论

固有频率理论包含两点重要结论[15-17],这两点结论与传感器刚度分布和质量分布结合,是固有频率模型建立的重要理论依据。

1)固有频率是物体的固有属性,由物体自身的性质(如质量、材质等)决定,与外界条件(如受力状态、约束状态以及空间状态等)无关。

2)固有频率仅与物体的刚度分布与质量分布有关,用公式表示为

式中:ω为物体的固有频率,rad/s;kp为刚度分布,N/m;mp为质量分布,kg。

1.2 传感器建模分析

四柱式传感器的结构外形如图1所示,四根立柱与上下端面为一体化结构,下端面作为固定端受到约束,上端面作为自由端受力。从形式上,每根立柱都可以简化为一个一端简支、一端自由的梁,可将其视为一个独立的测量单位[1]。

图1 四柱式传感器外形示意图Fig.1 Outline diagram of four-column sensor

研究传感器的测量原理可知,外部载荷传递到弹性体上的最终结构为贴片的四根立柱,四柱式弹性体的动态性能主要与四根立柱的动态性能有关。

分析图2所示的传感器的模态仿真结果可知,弹性体下端面不参与频率响应过程,上端面模态频率响应复杂且不稳定,均无法作为弹性体固有频率模型建立的主要对象;而四根立柱模态分析结果显示其固有频率响应集中且稳定,对频率响应分析起主导地位,可作为四柱式传感器固有频率模型建立的主要对象。

图2 四柱式传感器模态频率分析图Fig.2 Modal frequency analysis diagram of four-column sensor

综合上述分析可知,传感器固有频率模型建立的主要对象为其四根立柱,最重要的建模步骤为将等效梁模型与传感器的质量分布与刚度分布分析相结合,得到四柱式传感器固有频率模型。

分析四柱式传感器的质量分布与刚度分布,建立起传感器整体固有频率与单立柱等效梁模型的固有频率的关系。四柱式传感器的立柱与上下端面为一体化连接,四根立柱相当于彼此“并联”,增加了其整体刚度。该结构并联形式为胡克定律中的弹簧串并联问题的外延范畴[18-20],整体并联系统的刚度为各子系统的刚度之和[18-20],故可知:弹性体的刚度分布约为每根立柱刚度分布的4倍。由图2所示的仿真图像可知,该结论正确。

可将四柱式传感器的每根立柱视为一个“独立的传感器”[1],该形式同样属于胡克定律中的并联系统运动问题外延范畴[18-20],结合传感器立柱贴片测量的方式,忽略维间微小耦合,假设工作时每根立柱自由振动不受其他立柱的状态影响,则传感器整体的质量为每根立柱自身的质量分布。图2所示的仿真图像表明,四柱式传感器的结构形式符合上述理论。

综合上述刚度分布与质量分布的分析,由固有频率定义式可知,弹性体整体的固有频率ωn与每根立柱的固有频率ω0的关系为

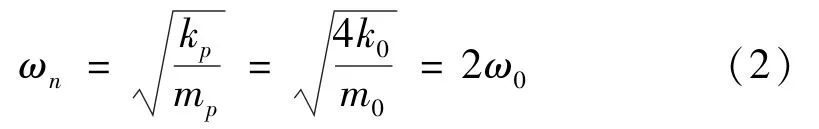
式中:k0为立柱刚度分布,N/m;m0为立柱质量分布,kg,mp=m0。

由式(2)可得传感器整体的固有频率约为每根立柱的2倍。

如图3所示,将沿径向方向的立柱横截面边长参数定义为长度参数l,沿周向方向的边长参数定义为宽度参数w,垂直于上下端面方向的柱体高度参数定义为高度参数h。

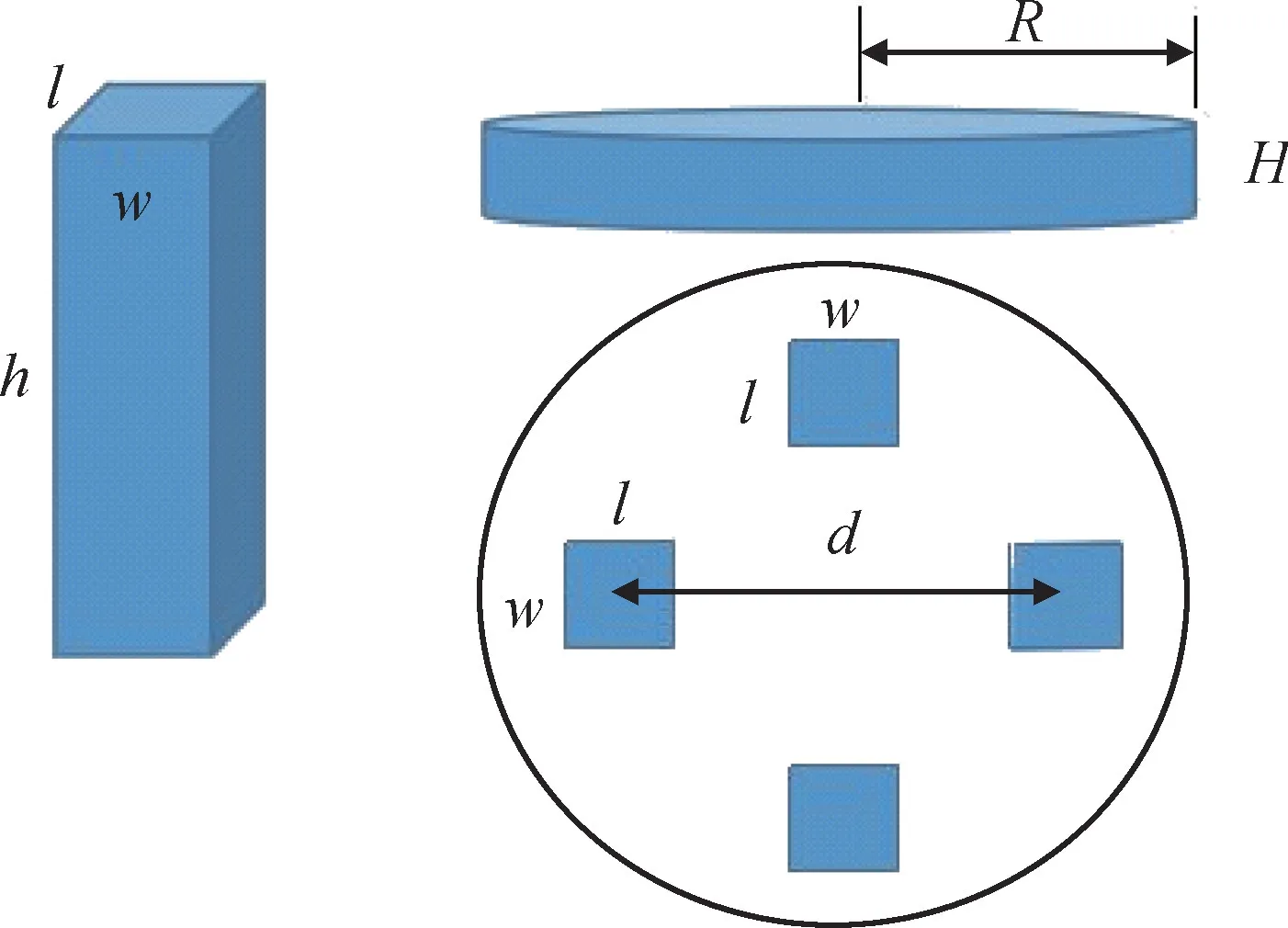
图3 四柱式传感器结构示意图Fig.3 Structure diagram of four-column sensor

建立等效梁模型的固有频率模型时,参照了胡海昌[21]的变分法研究过程,并应用在四柱式传感器固有频率模型的研究中。

线性弹性体在没有外力作用的情况下作固有振动,设应力分量的振幅为σx,σy与σz,位移分量的振幅为u,v和w,圆周频率为ω,运动方程为

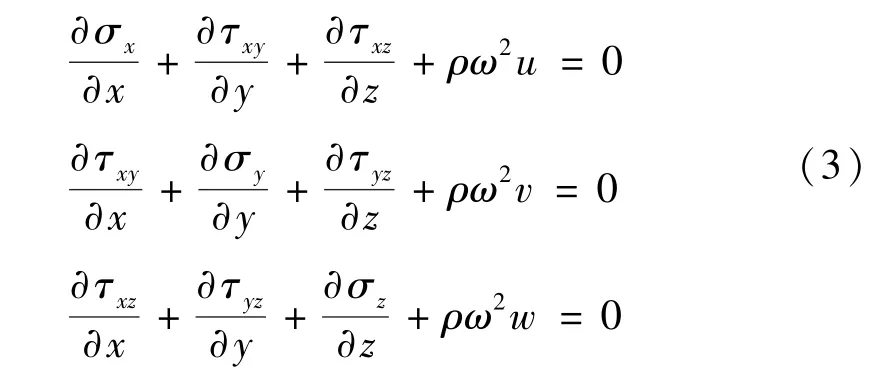
进行变分法求解可得线性弹性体的各阶固有频率计算式为

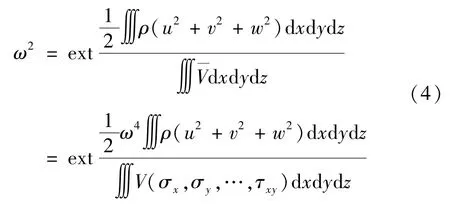
式(4)的最小极值与一阶固有频率唯一对应,其极值从小到大依次排列即为物体的各阶固有频率。

在得到了一般线性弹性体的固有频率公式后,可再对其引入一般线性均匀直梁的约束条件,进而获得一般线性均匀直梁的固有频率公式。再通过对其加入相应的等效梁模型的约束条件,最终获得等效梁模型的固有频率公式为

由前述结论,弹性体整体的固有频率约为每根立柱的2倍,将角频率公式转化为圆频率公式,并将截面惯性矩式展开,得到弹性体的固有频率模型为

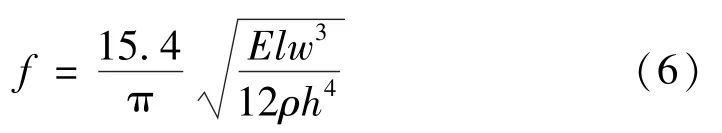
式中:f为四柱式传感器固有频率,Hz;l为四立柱长度参数,m;w为宽度参数,m;h为高度参数,m;E为材料弹性模量,Pa;ρ为密度,kg/m3。

由式(6)可知,提高四柱式传感器固有频率的方法有两类:改进四柱式传感器的结构参数和改进制成传感器材料参数,其中第一类方法为本研究的重要内容,第二类方法属于其他学科范畴,不作为本文研究内容。

2 仿真研究

为验证理论研究结论的正确性即(增大四立柱长度参数l,增大四立柱宽度参数w,减小四立柱高度参数h可使四柱式传感器固有频率提升,反之亦然),通过Solidworks有限元仿真软件对四柱式传感器固有频率与其结构参数的关系进行分析,整个仿真工作对下端面进行固定约束,各结构参数变化时,不会出现柱体相交接触等问题。

2.1 仿真研究对象

以某型四柱式传感器的四柱式弹性体为仿真研究对象,其初始结构尺寸(四立柱的长×宽×高)为15×15×20 mm,上端面尺寸为直径105 mm,厚度H=20 mm。四立柱间距d=65 mm。

四柱式弹性体的材料为合金材料40GrNiMoA,该材料具有低滞弹性与低蠕变特性。其弹性模量E为2.09×1011Pa,密度ρ为7830 kg/m3。

2.2 初始结构仿真

对初始结构的四柱式传感器固有频率进行有限元仿真计算,以该仿真结果作为后续仿真研究的对比对象与评价传感器结构参数改进后固有频率提升效果的基准。四柱式弹性体固有频率的仿真结果与其实验经验结果相近,如表1所示,并且理论结果与仿真结果间的相对误差较小,理论模型的研究结论可作为仿真研究的指导。

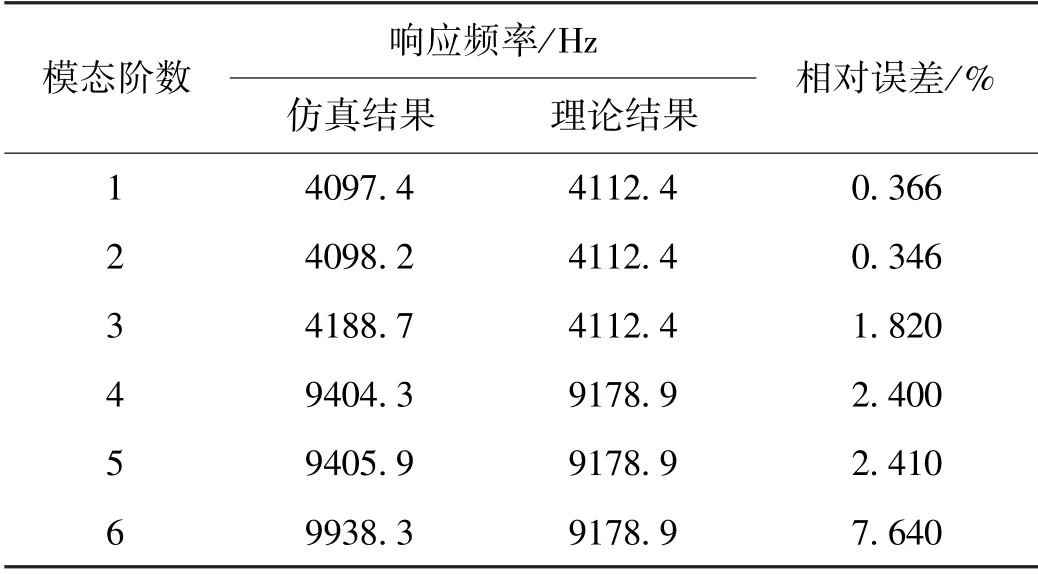
表1 四柱式弹性体各阶响应频率Tab.1 Response frequency of four-column elastomer at each order

2.3 长度参数变化仿真

四柱式弹性体的立柱外形较为简单,忽略导角类结构,可将其简化为一根长方形柱体。研究四立柱结构参数改变时其固有频率变化,应考虑四立柱对称,对其进行相同的结构参数变化。

对四立柱长度进行变化的方法主要包括内扩和外扩两类,如图4所示,保持四立柱内侧面位置不变,沿上下端面半径方向向外增大l,称为外扩;保持四立柱外侧面位置不变,沿上下端面半径方向向内增大l,称为内扩。

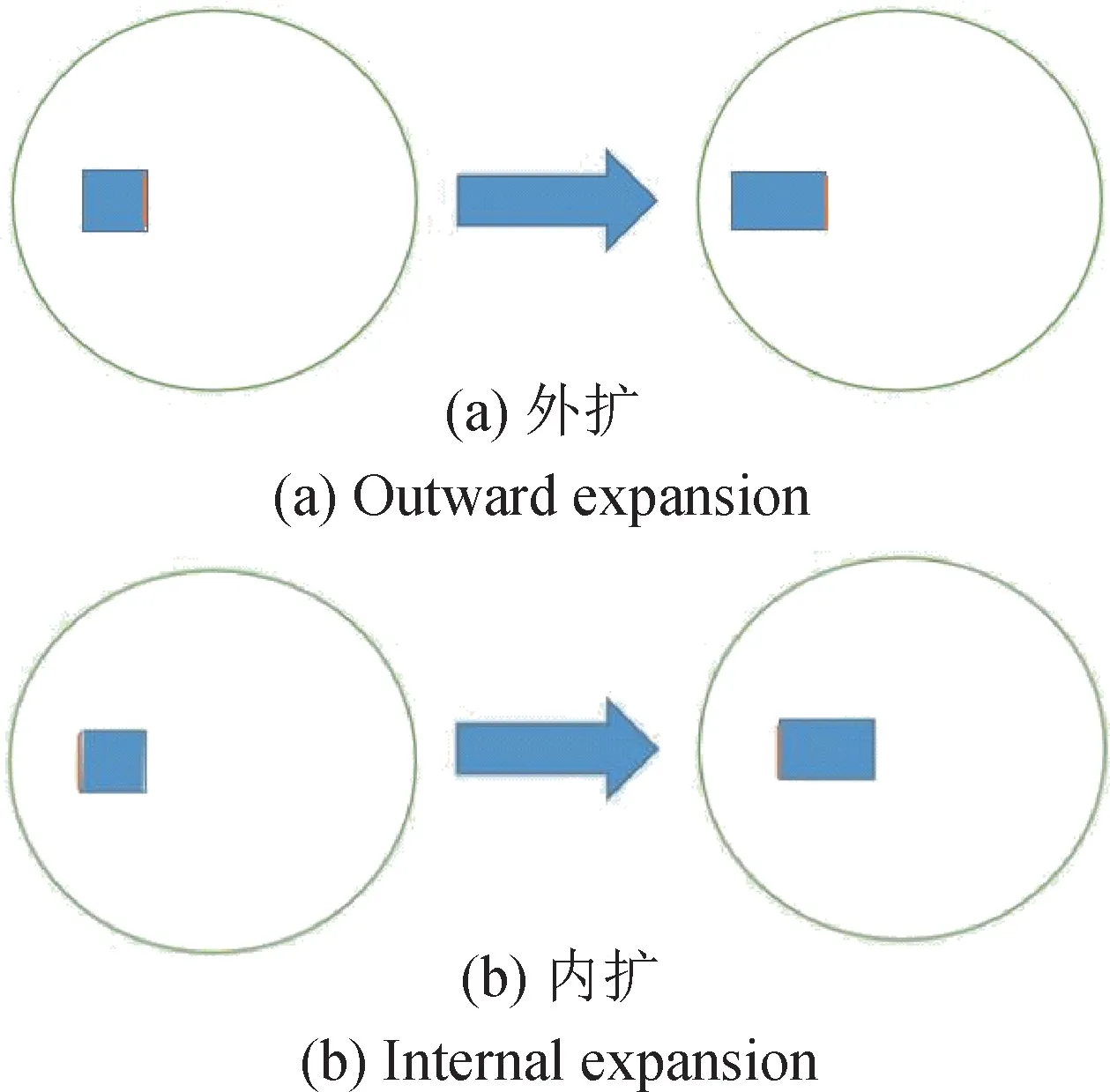
图4 立柱长度参数变化示意图Fig.4 Schematic diagram of column length parameter change

为研究外扩及内扩条件下传感器固有频率的变化,分别外扩5 mm与10 mm,内扩5,10,15 mm,并在Solidworks仿真软件中画出相应结构的四柱式传感器模型,并对其进行有限元仿真,分析其各阶固有频率。外扩仿真结果见表2。

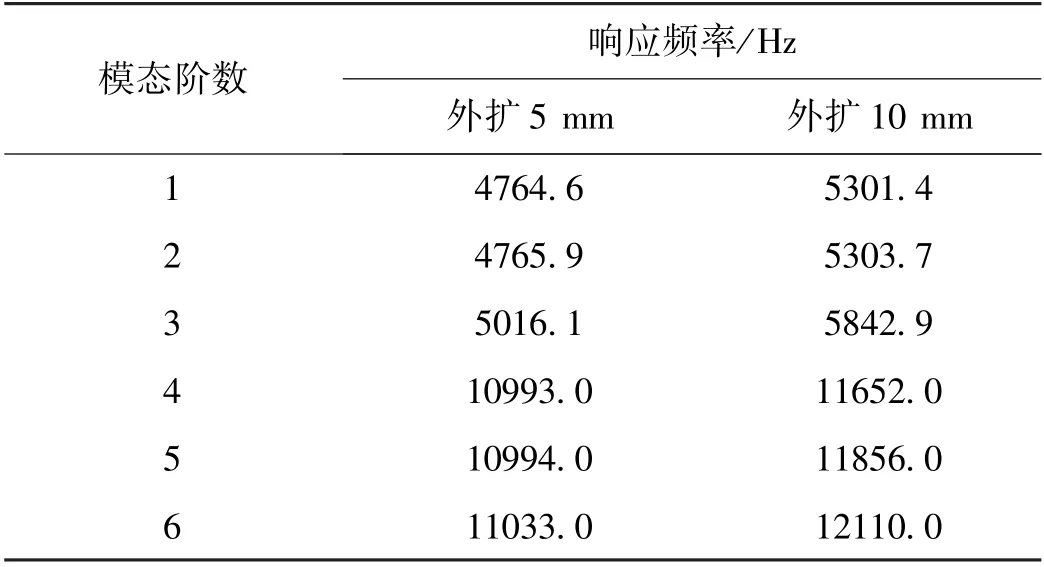
表2 外扩后的各阶响应频率Tab.2 Response frequency of expanded at each order

由仿真结果可知,外扩后的四柱式传感器与原结构的传感器相比,固有频率得到了提高。且外扩10 mm条件下,四柱式传感器的各阶固有频率提高更多。图5所示的固有频率随外扩参数变化示意图也显示,四柱式传感器的固有频率随外扩参数的增加而增加。

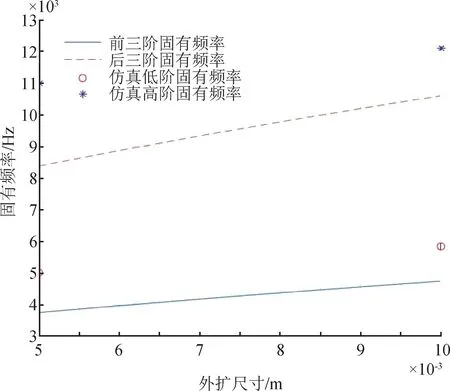
图5 固有频率随外扩参数变化示意图Fig.5 Schematic diagram of natural frequency variation with external expansion parameters

表3为内扩5,10,15 mm后三款四柱式传感器的各阶固有频率。

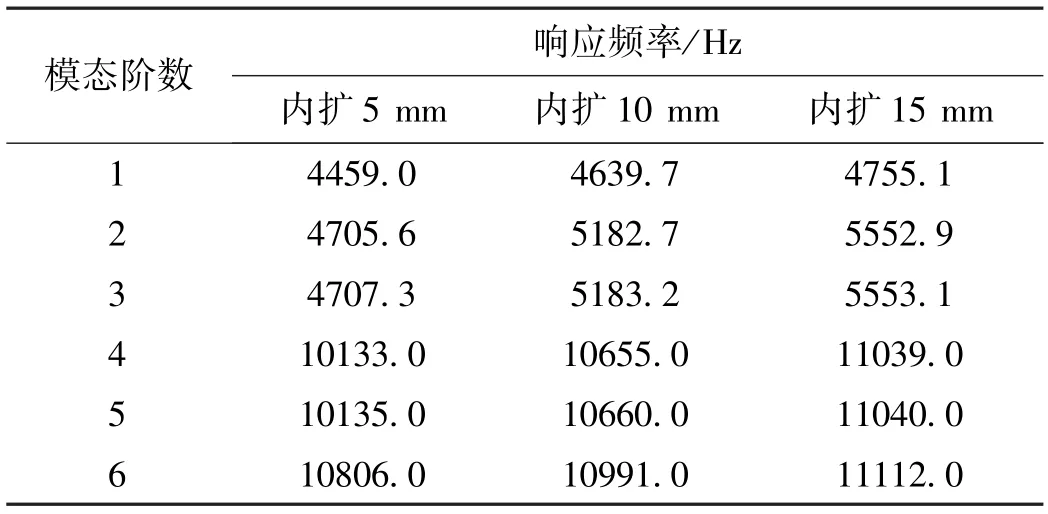
表3 内扩后的各阶响应频率Tab.3 Response frequency of internal at each order

仿真结果表明,分别内扩5,10,15 mm后的四柱式传感器,与原结构的四柱式传感器相比,其各阶固有频率均得到了提高,并且,图6所示的固有频率随内扩参数变化示意图也表明,四柱式传感器的内扩尺寸越大,其固有频率越高。

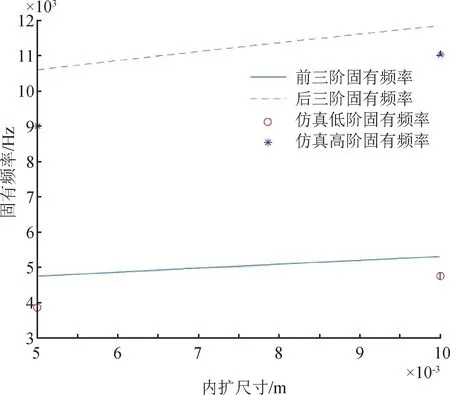
图6 固有频率随内扩参数变化示意图Fig.6 Schematic diagram of natural frequency variation with internal expansion parameters

综上所述,无论内扩还是外扩,只要传感器立柱长度参数l增大,传感器的固有频率就会提高,并且传感器的固有频率随立柱长度参数l增大而增加,这与理论研究的结论相同。

2.4 宽度参数变化仿真

对四立柱进行宽度参数w变化的仿真研究,以验证其对固有频率的影响。将w分别增大15 mm和25 mm,仿真分析各阶固有频率,结果如表4所示。

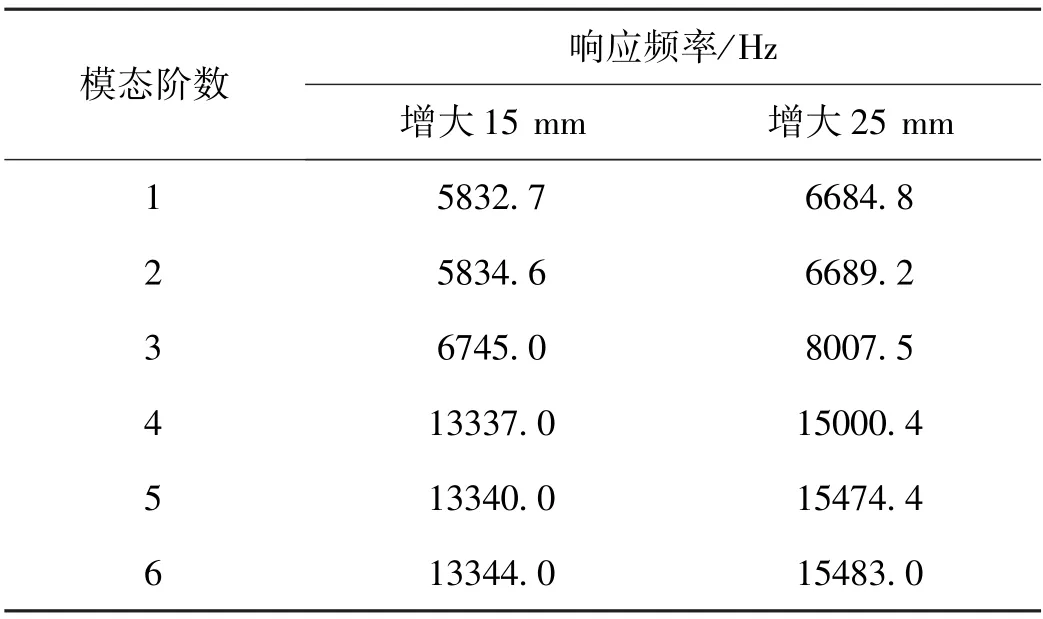
表4 w增大后的各阶响应频率Tab.4 Response frequency of increase w at each order

仿真结果与图7所示的固有频率随宽度参数变化示意图表明,传感器固有频率随着立柱宽度参数w增大而提高。该仿真研究的结论与理论研究结论一致。

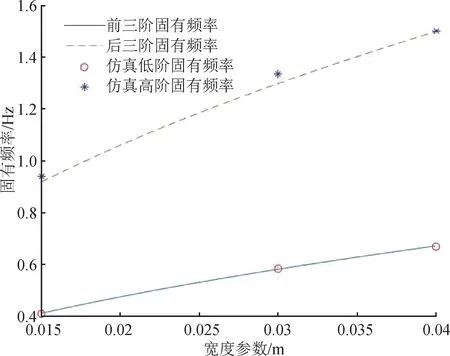
图7 固有频率随宽度参数变化示意图Fig.7 Schematic diagram of variation of natural frequency with width parameters

2.5 高度参数变化仿真

通过改变四立柱的高度进行相应结构参数下的固有频率仿真,验证立柱高度参数变化对各阶固有频率的影响。对立柱高度参数h分别抬高与降低10 mm后的四柱式传感器进行有限元仿真分析,各阶仿真固有频率结果如表5所示。

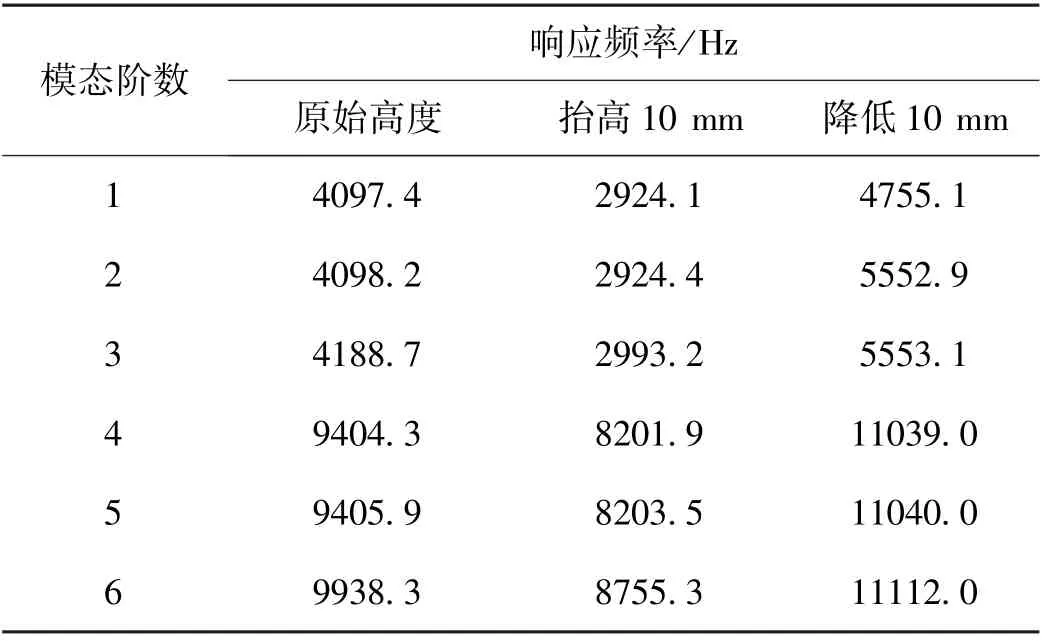
表5 h变化后的各阶响应频率Tab.5 Response frequency of h column at each order

由表5所示的仿真结果与图8所示的固有频率随立柱高度参数变化的示意图可知,传感器固有频率随着立柱高度参数h减小而提高。该结论与理论研究结论一致。

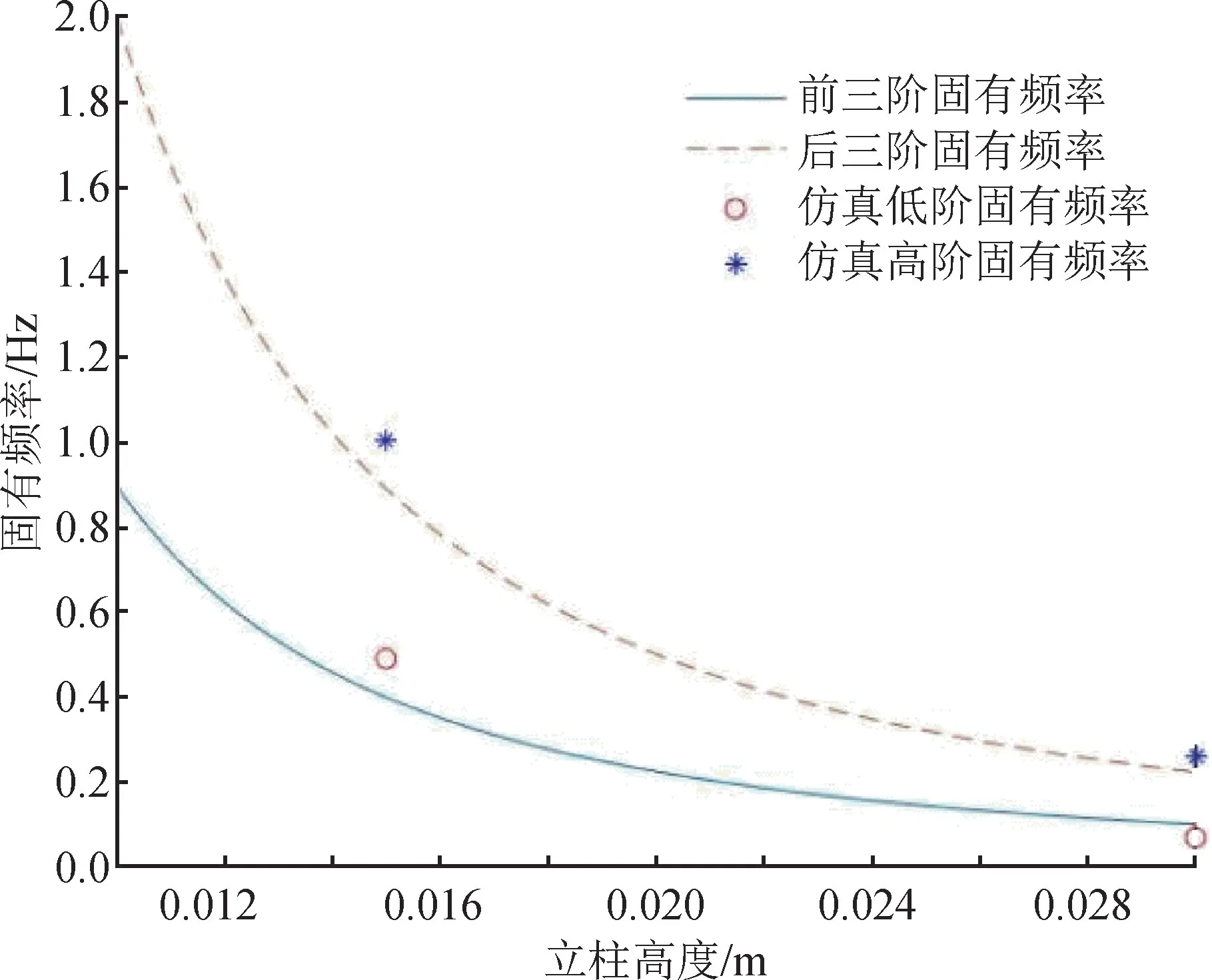
图8 固有频率随高度参数变化示意图Fig.8 Schematic diagram of variation of natural frequency with height parameters

3 实验验证

基于理论与仿真研究结论,对现有四柱式弹性体进行了改进研制,设计上增大了其四立柱横截面边长(即长度参数l与宽度参数w),减小了四立柱高度参数h,改进前后各结构参数如表6所示。

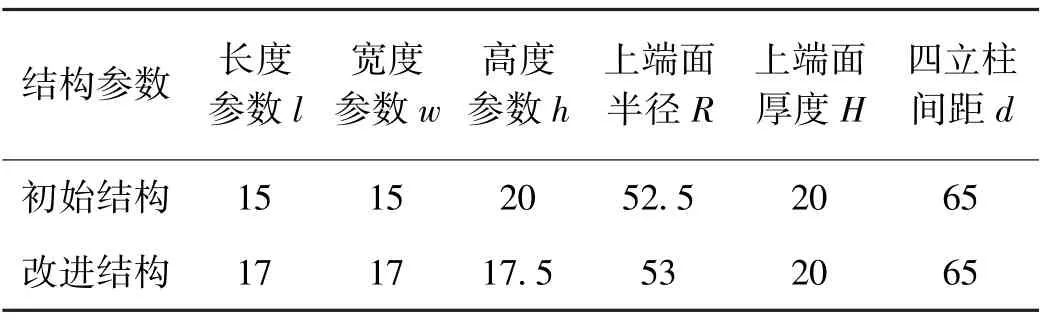
表6 改进前后结构参数对比Tab.6 Comparison of structural parameters before and after improvement

对改进前后的四柱式传感器进行标准锤击法实验,标准锤击法的原理为通过力锤敲击获取脉冲激励信号,来对传感器进行激励与测量。实验测试了对传感器动态性能影响最大的Z轴振荡固有频率(第六阶固有频率),改进后的四柱式传感器实验响应波形曲线如图9所示。测试得到的四柱式传感器改进前后的固有频率与理论固有频率的相对误差分析如表7所示。

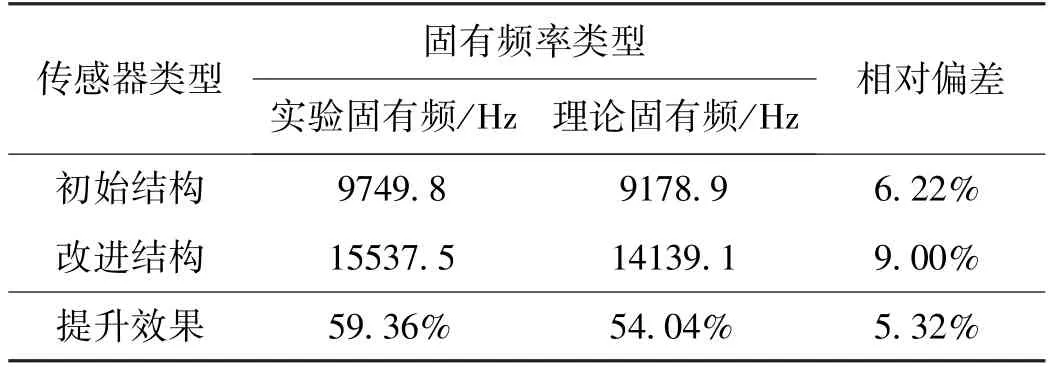
表7 初始结构与改进结构固有频率对比与分析Tab.7 Comparison and analysis of natural frequencies between initial structure and improved structure

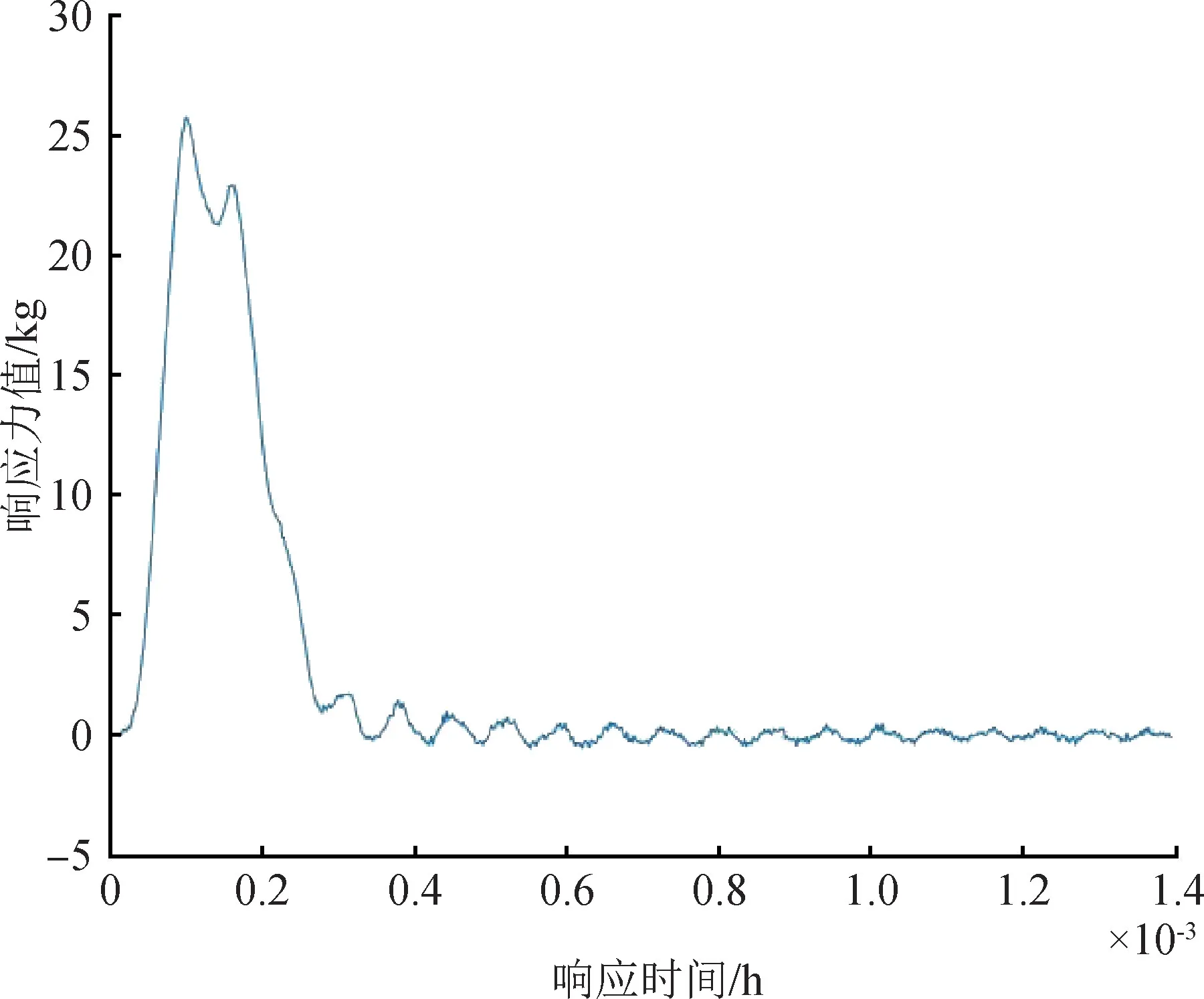
图9 实验响应波形图Fig.9 Experimental response waveform

该实验结果验证了理论与仿真研究结论的正确性,在保证不牺牲传感器大量静态性能的前提下,将四柱式传感器的固有频率由9749.8 Hz提升至15537.5 Hz,即提升了近50%的固有频率,进而使动态测试的工作频率范围与动态力值变化的跟随性能得到了提升。

4 结论

本文通过改进四柱式力传感器的结构参数来提升传感器固有频率,结合理论分析、仿真研究与实验研究,提出了通过改变四柱式力传感器结构参数和材料参数的方法来提升固有频率,为今后改进、设计高动态性能四柱式传感器奠定了基础。由于目前应用的四柱式力传感器材料的性能符合静态力学指标,故不能通过更换材料的方法来提升传感器动态性能,且材料改进研究也不属于本学科研究内容,故改进材料参数的研究结论可作为辅助手段与进一步优化应用的方向。