弹性-滑动减震体系地震残余位移影响因素研究

2021-02-11周琦智袁和芬李建中后钰敏

结构工程师 2021年6期

周琦智袁和芬李建中，* 后钰敏

（1.同济大学桥梁工程系，上海 200092；2.云南功东高速公路建设指挥部，昆明 650000）

0 引言

桥梁是交通系统中的生命线，在震后有必要保证其基本作用。对桥梁结构采用减隔震技术，可以降低结构所受地震的影响，减少桥梁在地震发生时发生破坏的可能性。减隔震体系一般是通过设置支座、耗能装置，控制结构的变形和耗能，从而达到保护上部结构、桥墩和基础不受损伤、在弹性范围内。

叠层橡胶支座和滑动摩擦支座都是常见的减隔震支座。叠层橡胶支座由薄橡胶片与薄加强钢板交替联结而成，且上下有翼缘，其横截面主要有圆形和矩形。滑动摩擦支座是一种滑动耗能的减隔震支座，以聚四氟乙烯为摩擦面，通过摩擦耗散地震能量。

随着减隔震技术的发展，出现了将叠层橡胶支座与滑动支座结合的减隔震装置［1］，该装置称为弹性-滑动减震（Resilient Sliding Isolation，RSI）体系。Iemura和Taghikhany等［2］对高速公路桥梁的弹性—滑动减震体系进行了研究，将其与天然橡胶支座对比，发现其减隔震性能更好。Iemura等［3］还通过振动台试验和建模分析对RSI体系进行了优化分析，确定不同允许加速度水平的最佳设计参数。

减隔震装置的恢复能力也越来越引起重视，这种能力是指其在地震发生后回到原来位置的能力，而地震后减隔震装置的残余位移是衡量震后其恢复能力的重要指标［4］。针对不同形式的减隔震装置，很多学者对其震后残余位移都进行了深入的研究。Katsaras等［5］对双线性模型的减隔震系统进行了参数分析，研究了地震后残余位移和连续地震后位移的积累对控制参数的依赖性。Ismail等［6］对一种针对近断层地震的隔震装置（RNC）的残余位移进行了评估，其具有的线性中心调节机制，可有效减小残余位移。Quaglini等［7-8］对摩擦摆系统的恢复能力与特征强度和刚度的关系、弯曲面滑动支座的残余位移影响因素进行了研究，并发现了初始偏移对残余位移的影响。还有研究［9-10］表明减隔震支座残余位移还受地震动特征以及地震峰值加速度的影响。

本文对影响弹性-滑动减震体系震后残余位移的因素进行了探究。以一连续梁桥为例，采用SAP2000进行有限元分析，选取了15条反应谱接近的地震波，采用非线性时程分析方法进行计算，改变弹性-滑动减震体系的摩擦系数和叠层橡胶支座刚度，探索其与支座最大位移、支座残余位移之间的关系，并分析影响体系残余位移的因素。

1 弹性-滑动减震体系

弹性-滑动减震体系由滑动摩擦类支座与叠层橡胶支座并联组成，滑动摩擦类支座提供竖向支承和摩擦耗能，叠层橡胶支座提供水平恢复力，如图1所示。

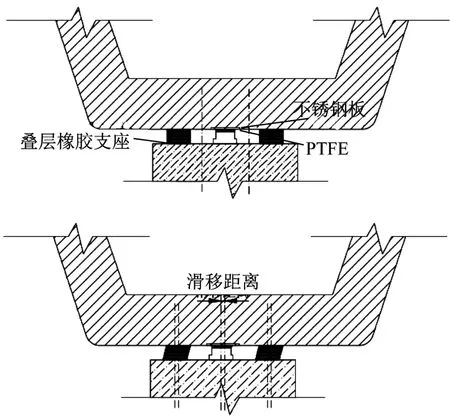
图1 弹性-滑动减震体系Fig.1 Resilient sliding isolation system

叠层橡胶支座滞回曲线形状呈狭长形，滞回曲线包络面积很小，几乎没有耗能能力。这与橡胶材料自身的弹性性能是密切相关的，而其滞回曲线面积主要来自于材料与构造的误差与不均匀。其滞回模型可近似作线性处理［11］，如图2（a）所示。

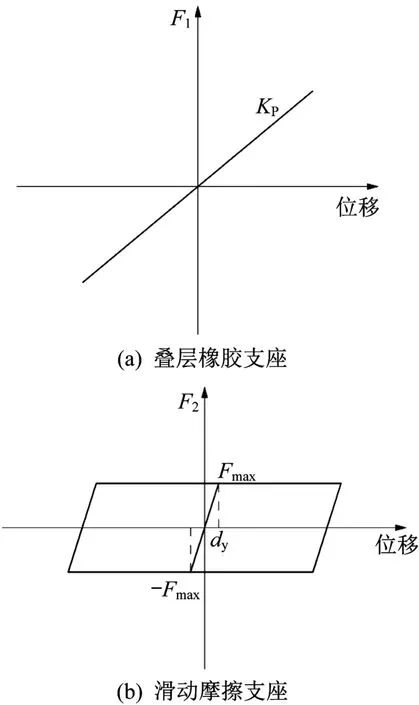
图2 支座滞回模型Fig.2 Hysteretic model of bearings

滑动摩擦支座在横向力超过临界滑动力后，发生滑动，摩擦耗能。它的滞回模型可以用双线性模拟［12］，如图2（b）所示。

其临界滑动力为

式中：μ为滑动摩擦支座的摩擦系数；W为支座反力（kN）。

初始刚度可以定义为

式中，dy为屈服位移。

由图2（b）可以看出，滑动摩擦支座处于滑动状态时，其屈后刚度为0，没有恢复力，容易造成支座震后较大的残余位移。

弹性-滑动减震体系的滞回模型可以由以上两种支座的滞回模型组合得到，如图3所示。图3为系统的滞回曲线，其有三个独立的重要参数，它们是零位移处的力F0（特征强度）、屈服后刚度KP和屈服位移dy［3］。其中，特征强度对体系的恢复能力具有重要影响［13］。体系的屈前刚度为叠层橡胶支座与滑动摩擦支座之和，屈后刚度为叠层橡胶支座的水平刚度，屈服位移等同于摩擦支座的屈服位移。

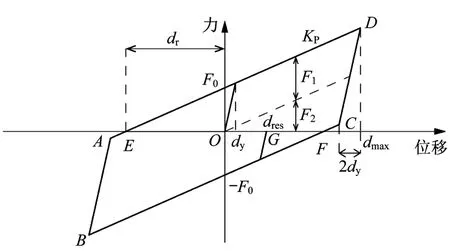
图3 弹性-滑动减震体系滞回模型Fig.3 Hysteretic model of resilient sliding isolation system

弹性—滑动减震体系的合力可以由两个分量，叠层橡胶支座的线弹性力分量F1和弹塑性分量F2组成。如图2（a）所示，线弹性力恢复力分量F1=Kpd，与位移成正比，方向指向原点。弹塑性分量F2在超过屈服位移后，保持为常量F0，方向与位移的变化方向（速度方向）相反，也就是说，其方向可能远离原点，从而产生较大的残余位移。

图3中，dr为最大静态残余位移，其值仅取决于系统性质，对于双线性滞回系统，它等于：

当dr减小时，减震系统的恢复能力变得更好。因为残余位移受到其限制，dr值较小意味着线性弹性分量占主导地位。相反，对于具有屈后刚度Kp等于零的情况（如滑动摩擦支座），dr的值趋于无穷大，这意味着这样的系统在任何位移下都可以处于静态平衡状态。

弹性—滑动减震体系的合力为零（弹性力分量F1和弹塑性分量F2合力为零）时，对应静态残余位移为dres，其临界为

2 工程背景与参数分析

2.1 工程背景

本文选用的实例是某一五跨连续梁桥，每跨跨径均为30 m，如图4所示。

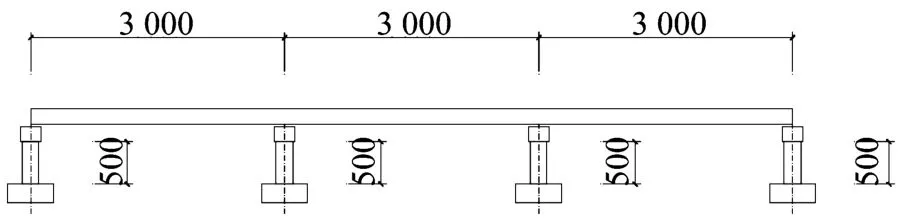
图4 桥梁跨径总体布置（单位：cm）Fig.4 Overall layout of bridge span（Unit：mm）

上部结构为预应力混凝土预制小箱梁，主梁采用C50混凝土，桥面宽25 m，采用上下行线整体式构造，横向共设6个小箱梁，桥面铺装厚100 mm，沥青面层厚90 mm，两道防撞护栏与中央分隔带的总质量共为2.6 t/m。

主梁与桥墩的连接采用弹性-滑动减震体系的支座，每个桥墩上左右对称布置两组弹性-滑动减震体系支座。

下部结构包括盖梁、桥墩与承台，桥墩采用单柱式，尺寸为2.0 m×2.0 m，高度均为5 m，在图4中从左到右依次编号1—4，承台下布置7根800 mm直径钻孔灌注桩。

2.2 有限元模型

采用SAP2000进行建模，桥墩盖梁主梁采用空间梁单元。支座方面，在有限元模拟中，利用弹簧单元，采用如图3所示的双线性模型对弹性-滑动减震体系进行模拟。基础采用固结的形式模拟。二期恒载以单元质量和点质量的形式添加在主梁上。参考《公路桥梁抗震设计规范》［12］，在承台底采用平动和转动共6个弹簧模拟模拟桩土相互作用效应，土弹簧刚度采用m法计算。建立的有限元模型如图5所示。

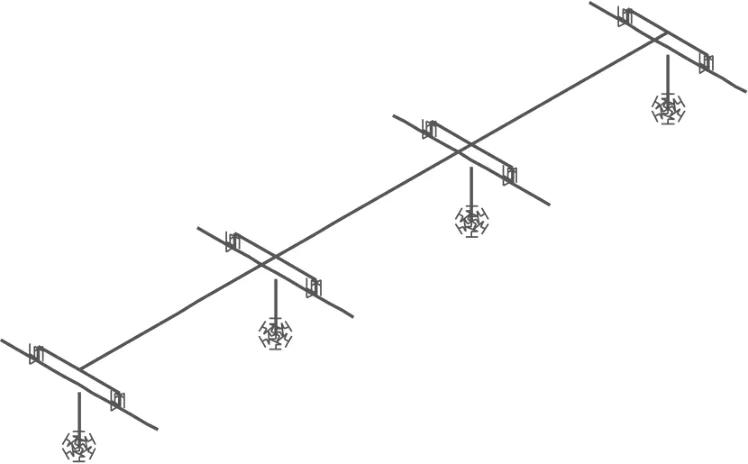
图5 桥梁有限元模型Fig.5 Finite element model of bridge

以摩擦系数和叠层橡胶支座刚度为参数，探究其对残余位移的影响。具体参数工况如表1所示。

表1 支座参数工况表Table 1 Cases of bearing parameters

2.3 地震动输入

从美国太平洋地震工程研究中心（PEER）强震数据库中选取了15条实际地震波作为地震输入，结果取15条地震波结果的平均值。选取的地震波均为距离断层10 km以外的地震动，根据对应反应谱进行选取，保证15条波的对应反应谱与目标反应谱接近，其对应反应谱情况如图6所示。

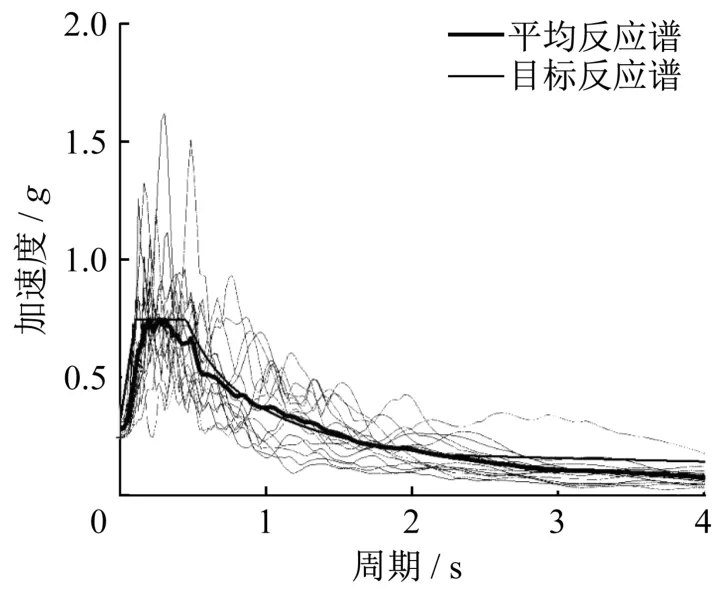
图6 地震波反应谱Fig.6 Response spectrum of seismic wave

选取地震波的最大峰值加速度（PGA）保证相近，平均地震峰值加速度为0.287g，震级、断层距离、峰值加速度情况等见表2。为了表征不同地震强度的作用，取不同的放缩系数1倍、2倍、3倍，对应的平均地震峰值加速度为0.287g、0.574g、0.861g。

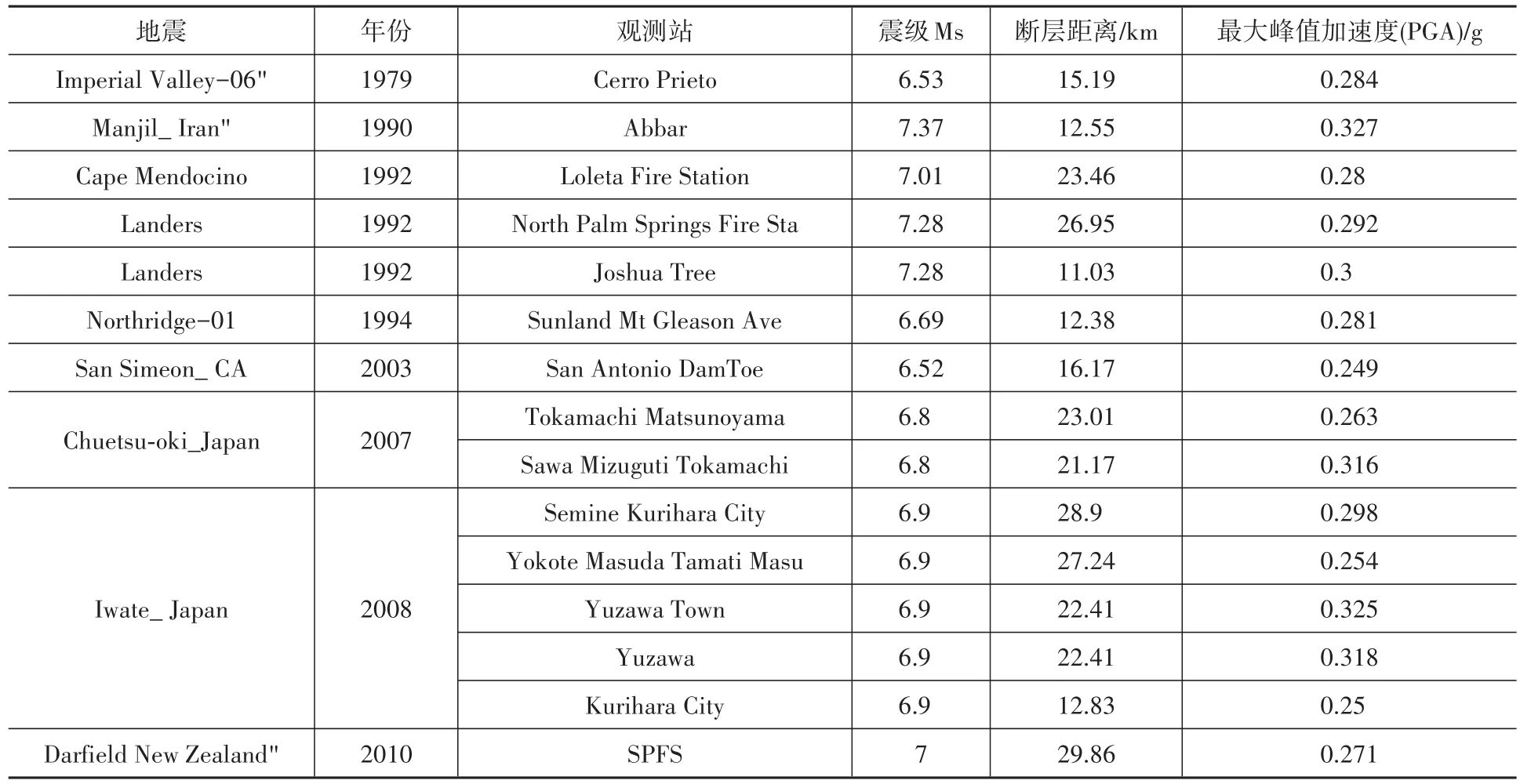
表2 地震波情况Table 2 Seismic wave conditions

3 参数分析

本文主要对弹性-滑动减震体系的最大位移dmax和残余位移dres进行分析，并考虑了不同支座的最大静态残余位移dr。本例中的工程背景是一座规则连续梁桥，每个桥墩上支座的位移都几乎一致，参数变化较多，这里选取2号桥墩上支座的纵桥向位移进行分析。地震波按比例取用了三种不同大小的地震峰值加速度，研究在不同地震强度情况下的参数分析规律。

3.1 摩擦系数参数分析

为研究摩擦系数变化对弹性滑动隔震支座残余位移的影响，通过变化擦系数得到不同情况下支座的最大残余位移、最大位移见表3。从表3中结果可以看到，随着摩擦系数的增大，支座的最大位移减小，而残余位移却不是单调变化。

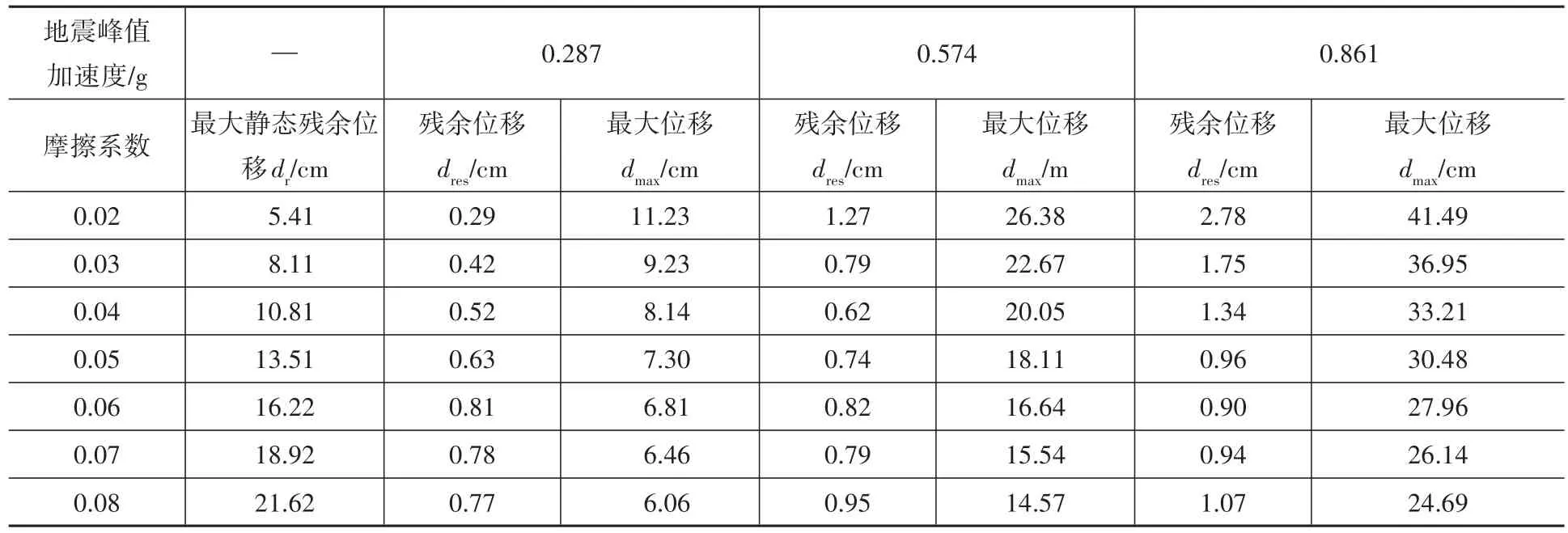
表3 不同摩擦系数下支座残余位移和最大位移Table 3 Residual displacement and maximum displacement of systems with different friction coefficient

最大静态残余位移dr与最大位移dmax之比随摩擦系数变化关系如图7所示，三条曲线分布代表了不同的地震波放缩系数情况下的结果，地震波系列1、2、3分别对应地震加速度峰值调整到0.287g、0.574g、0.861g的情况。从图7中可以得到，随着摩擦系数的增大，dr／dmax增加。因为随着摩擦系数的增大，体系的恢复力中的弹塑性分量F2增大，导致了其最大静态残余位移dr会增大；而较大的摩擦系数会导致摩擦力的增大，增强了体系的耗能能力，从而引起最大位移的减小，故dr／dmax随摩擦系数增加而增大。地震强度的增加会导致比值的降低，是因为随着地震作用强度的增大，最大位移会增大，而最大静态残余位移为系统的固有特性，dr不发生变化，故dr／dmax随地震作用的增加而减小。

图7 dr／dmax随摩擦系数变化规律Fig.7 Variation laws of dr／dmaxwith friction coefficient

残余位移dres与最大位移dmax之比随摩擦系数变化关系如图8所示。从图8中可以看出，在强度较高的地震作用下，残余位移与最大位移的比值与摩擦系数的关系表现为振荡关系，且均小于0.1。在地震强度较高的情况下，虽然随摩擦系数的增加，残余位移的变化表现为有增有减，而同时随摩擦系数增加，最大位移有所减小，导致残余位移与最大位移的比值随摩擦系数的增加表现为振荡关系。而在强度较低地震作用下，其比值随摩擦系数增大而增加，且在摩擦系数大于0.06后，其比值大于0.1。其原因在于，摩擦系数的增大，会导致弹塑性分量F2的增大，而F2的方向与速度方向相反，其在运动过程中存在远离原点的方向，可能会导致残余位移增大。而当地震作用不大时，其最大位移的变化随摩擦系数改变幅度较小，残余位移对这一比值的影响更大。因此，较大的摩擦系数会导致体系恢复能力减弱，但是较强的地震作用可能增强体系的恢复能力，在较强的地震作用下，dres／dmax随摩擦系数变化表现为振荡变化。

图8 dres／dmax随摩擦系数变化规律Fig.8 Variation laws of dres／dmaxwith friction coefficient

残余位移与最大位移之比dres／dmax随最大静态残余位移与最大位移之比dr／dmax变化关系如图9所示。由图9可以看出，不同地震强度下的关系曲线相当接近，但是地震强度越大，其曲线在图像中更左侧的位置，即dr／dmax的值越小。当dr／dmax小于2时，残余位移dres与最大位移dmax的比值较小，小于 0.1。而当dr／dmax取到 0.5时，dres／dmax的值更小。这表明dr／dmax较小时，体系的恢复能力较强。另一方面，dr／dmax随摩擦系数增大而增大，也就说明了对于弹性-滑动减震体系而言，较大的摩擦系数可能会导致体系恢复能力的减弱。

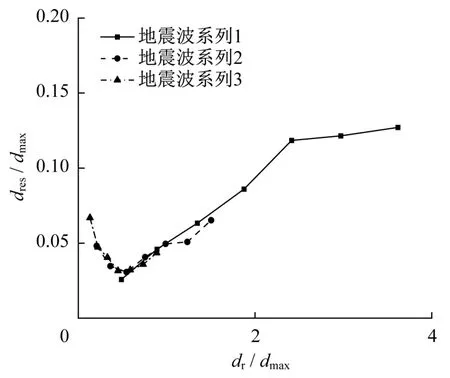
图9 摩擦系数分析中dres／dmax随dr／dmax变化规律Fig.9 Variation laws of dres／dmaxwith dr／dmaxin friction coefficient analysis

4.2 叠层橡胶支座刚度参数分析

叠层橡胶支座刚度的参数分析结果如表4所示。从表4中的结果可以看出，虽然随着橡胶支座刚度的增大，支座的最大位移dmax与摩擦系数的变化一样，为逐渐增大，但是残余位移dres的变化却呈现一个减小的趋势。特别是橡胶支座刚度由500 kN/m增大到2 500 kN/m的过程中，残余位移dres的减小特别明显：在0.287g的地震峰值加速度（PGA）下，残余位移由1.21 cm减小到0.24 cm；0.574 g的PGA下，残余位移由1.71 cm减小到0.63 cm；0.861 g的PGA下，残余位移dres由3.66 cm减小到1.41 cm。初步说明橡胶支座刚度较大时，恢复能力可能更强，体系的残余位移更小。

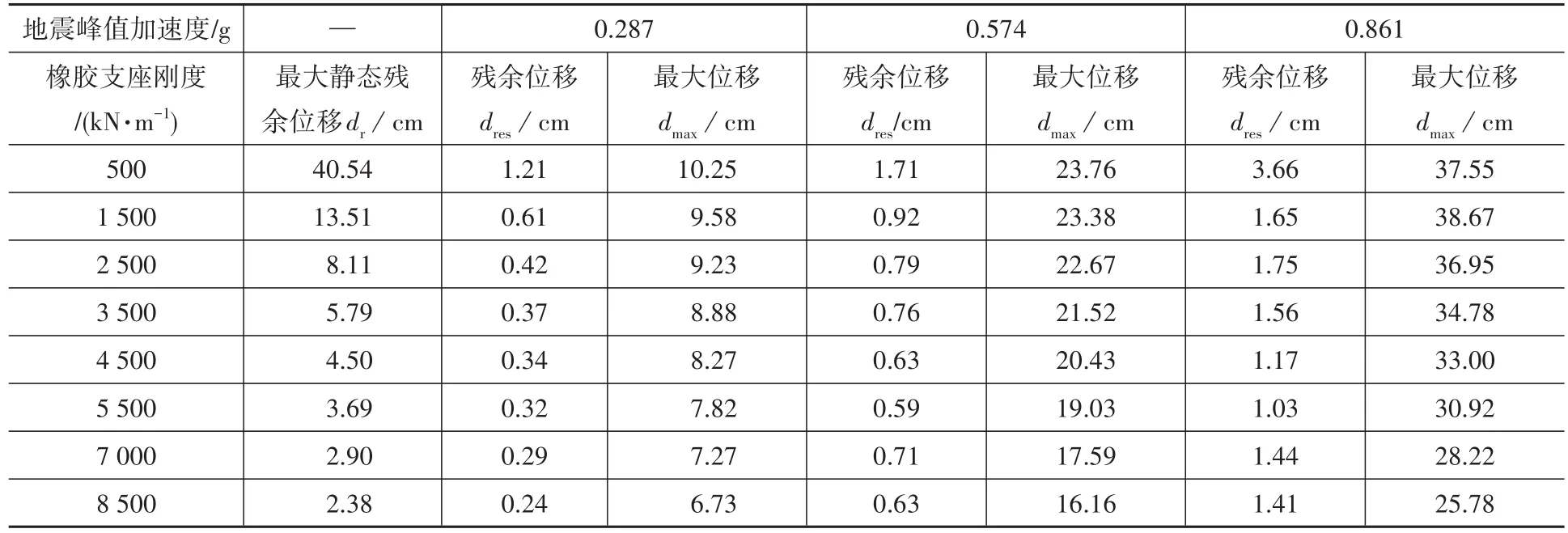
表4 不同支座刚度下支座残余位移和最大位移Table 4 Residual displacement and maximum displacement of systems with different stiffness

根据结果数据可以得到，最大静态残余位移dr与最大位移dmax之比随叠层橡胶支座刚度变化关系如图10所示。从图10可以得到，dr与dmax的比值随着橡胶支座刚度的增大而减小。这与摩擦系数的关系刚好相反。因为橡胶支座刚度的增加，能有效增大线弹性力分量F1，从而导致最大静态残余位移dr的减小。由于体系的刚度有所增大，体系的最大位移dmax的也随着减小，但是其减小的程度不如dr明显，故dr与dmax的比值随着橡胶支座刚度的增大而减小。

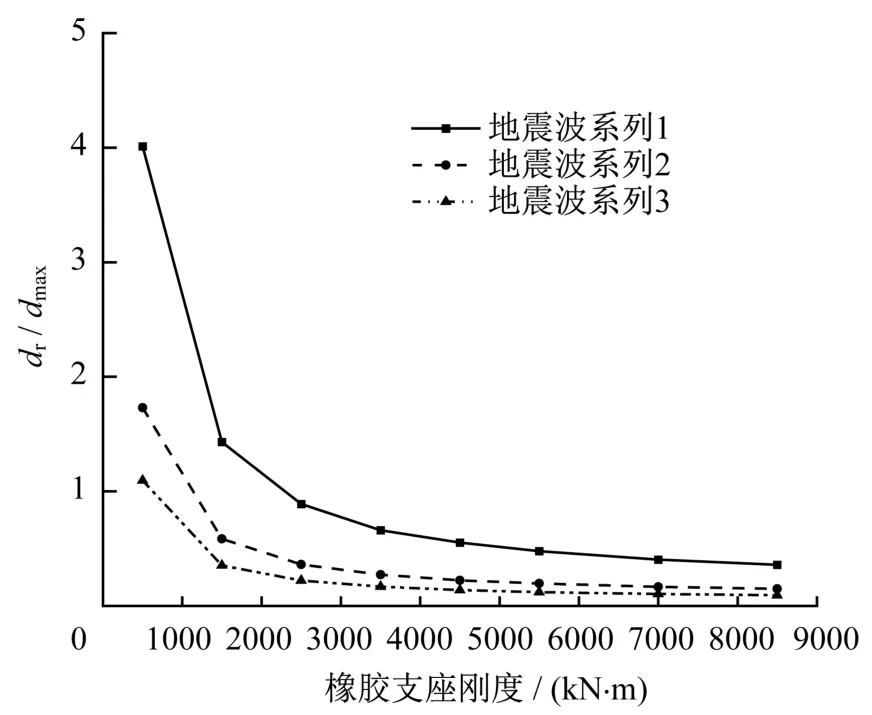
图10 dr／dmax随叠层橡胶支座刚度变化规律Fig.10 Variation laws of dr／dmaxwith laminated rubber bearing stiffness

残余位移dres与最大位移dmax之比随叠层橡胶支座刚度变化关系如图11所示。当橡胶支座刚度较小时，dres／dmax随橡胶支座刚度减小而增大。在PGA为0.287 g时，橡胶支座刚度由最小刚度500 kN/m增大到最大刚度8 500 kN/m，dres／dmax的比值由0.12减小到了0.036。说明了橡胶支座刚度较小时，体系在地震作用下的恢复情况较差，体系的恢复能力较弱。因为橡胶支座刚度增大能增大体系的线弹性力分量F1，而F1的方向始终指向原点，这有助于提高体系的恢复力，有效减少体系在震后的残余位移。但是当橡胶支座的刚度较大时，体系的屈后刚度明显增大，最大位移也会有较大的减小，因此dres／dmax在橡胶支座刚度较大时的变化不如在其刚度较小时的变化明显。此外，在较强的地震作用下dres／dmax也较小。

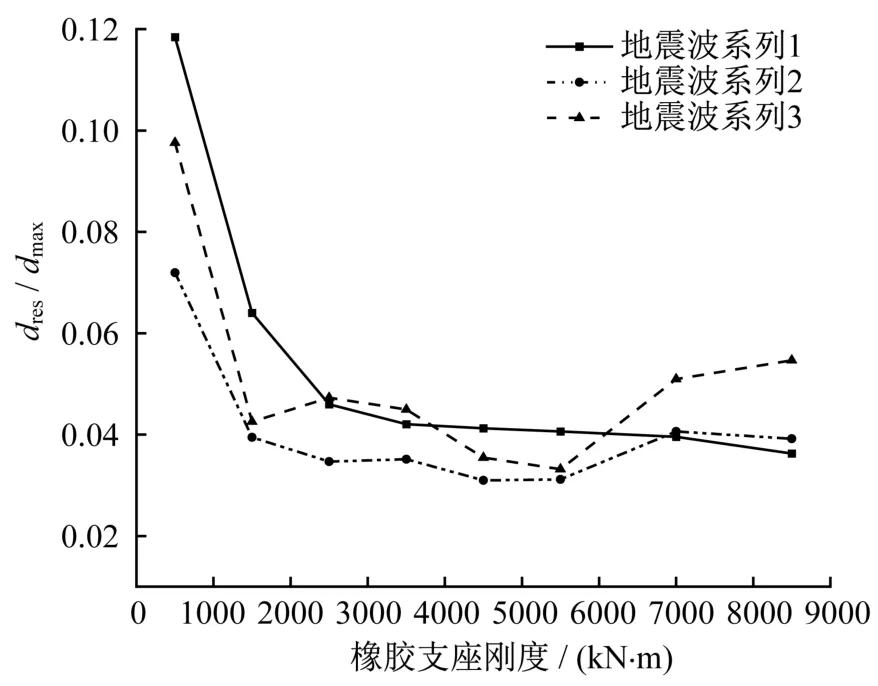
图11 dres／dmax随叠层橡胶支座刚度变化规律Fig.11 Variation laws of dres／dmaxwith laminated rubber bearing stiffness

残余位移与最大位移之比dres／dmax随最大静态残余位移与最大位移之比dr／dmax变化关系如图12所示。与摩擦系数变化的规律相同，当dr／dmax较小时，dres／dmax的比值小。当dr／dmax小于 2时，残余位移dres与最大位移dmax的比值均小于0.1，这表明dr／dmax较小时，体系的恢复能力更强。

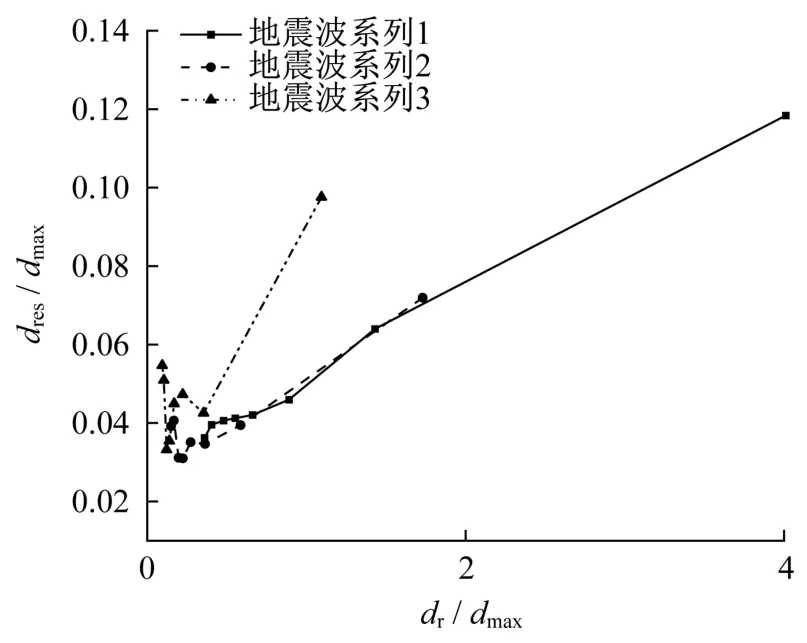
图12 橡胶支座刚度分析中dres／dmax随dr／dmax变化规律Fig.12 Variation laws of dres／dmaxwith dr／dmaxin laminated rubber bearing stiffness analysis

另一方面，dr／dmax随橡胶支座刚度的增大而减小。也说明了橡胶支座刚度的增大能增强体系的恢复能力。因为橡胶支座刚度的增大能增大体系的线弹性力分量F1，而F1方向始终指向原点，能有效减少震后残余位移，增强体系恢复能力。地震峰值加速度的增大也能减小dr／dmax的比值，说明了地震作用越强，体系恢复能力可能越强，这与之前的结论一致。