考虑节点域轴向滑移刚度的K6型单层球面木网壳稳定性分析
2021-02-11孙小鸾瞿以恒陆伟东
孙小鸾 瞿以恒 陆伟东
(南京工业大学建筑工程系,南京 210009)
0 引 言
在现有的单层球面木网壳的连接节点中,主要以在连接区的钢毂上焊接钢板,并结合螺栓连接的销式节点居多[1],如图1所示。但由于木材和钢材的材料差异,以及螺栓与木材之间的承压滑移变形,导致钢板螺栓节点在受力时易发生明显的轴向变形。特别是对于大跨度木网壳,各杆件承受轴力较大,且节点数量多,节点的轴向滑移变形更加显著,极易造成结构内力重分布,进而影响到木网壳的承载力及破坏模式。

图1 木网壳结构典型节点Fig.1 Typical joints in timber shell structures
在钢结构网壳研究中,对于不同的节点形式,众多学者针对节点的转动刚度开展了大量研究[2-4]。但焊接空心球节点、螺栓球节点或嵌入式毂节点等钢结构网壳常用节点,在受力时均无明显的轴向滑移变形。因此,钢网壳领域考虑节点轴向滑移刚度对结构整体稳定性影响的研究较少。
目前,针对木结构网壳节点刚度特性,也主要以转动刚度研究为主,或仅考虑轴力对节点转动刚度及弯曲承载力的影响。刘志周[5]对一种基于螺栓-钢夹板节点改进的木网壳节点开展了不同轴力作用下的转动刚度研究。在三参数幂函数模型的基础上,通过引入折减系数实现对不同轴力作用下节点弯矩-转角曲线的预测。周华樟等[6]对K6型球面木网壳的Varax节点在4种不同轴力工况下的节点受弯承载性能进行了试验研究,拟合得到了节点弯矩-转角关系方程。López等[7]对螺栓球节点网壳进行了节点及整体结构试验,提出了考虑不同节点转动刚度的网壳稳定承载力理论模型,并对矢跨比、杆件长细比等参数对网壳稳定承载力的影响进行了评估。何敏娟等[8]将螺栓-钢填板节点抗弯性能试验所得的弯矩-转角曲线按不同受力阶段简化为四折线方程,并在ANSYS中采用非线性弹簧单元进行模拟,分析了节点转动刚度对单层木网壳性能的影响。
在考虑节点轴向滑移变形对结构整体力学性能影响的研究方面,杨风利[9]利用ANSYS软件建立了考虑螺栓节点域轴向滑移变形的输电铁塔有限元模型,采用Combin39非线性弹簧单元模拟杆件连接节点处的轴向变形特性。研究发现,节点的轴向滑移变形会影响结构的内力分布并对整体变形产生较大影响。对于大跨木网壳结构,杆件轴力显著提升,连接节点处更易发生滑动变形,需引起重视并开展相关研究。
本文采用ANSYS中的APDL语言建立了K6型单层球面木网壳模型。通过Combin39非线性弹簧单元的参数设置实现对连接节点各向刚度的模拟,同时考虑节点的转动刚度和轴向滑移刚度,开展整体模型全过程稳定承载力分析,得到不同节点轴向滑移刚度对K6型球面木网壳稳定性能的影响。
1 分析模型
为同时考虑节点轴向滑移刚度及转动刚度,选用Combin39非线性弹簧单元进行模拟。Combin39单元可通过设置实常数对节点的刚度变化进行模拟,通过KEYOPT命令对弹簧单元的自由度方向进行设置。由于木网壳节点处的钢毂刚度较大,可忽略其自身变形,有限元模型中将其简化为节点。钢节点域杆件、胶合木杆件均采用Beam189梁单元模拟。
通过在节点处设置两根重合的、单元长度为10 mm的单自由度Combin39弹簧单元以考虑节点轴向滑移刚度及转动刚度,并对其余四个转动及平动自由度进行耦合约束,完成节点刚度的模拟,如图2所示。

图2 网壳杆件模拟图Fig.2 Simulation of shell members
本文选择100 m跨度的单层球面木网壳为基本研究对象,矢跨比取1/5,分频数取12,胶合木杆件截面尺寸取210 mm×800 mm,节点构造详见图3。钢节点域长度根据实际构造,定义为钢毂中心至螺栓群形心的距离,取400 mm,材料定义为钢材。网壳的整体有限元模型如图4所示,将其定义为S100模型。通过将模型中弹簧轴向刚度设置为木构件全截面轴向刚度模拟不考虑节点轴向刚度的网壳模型,将其定义为S100s模型,用于分析结果的对比。
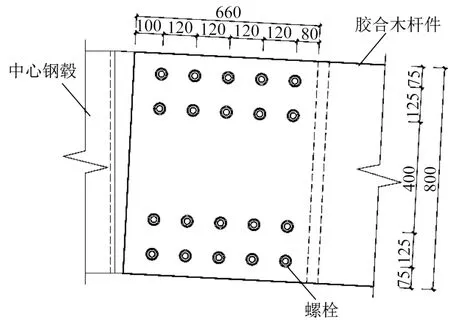
图3 节点构造Fig.3 Joint arrangement

图4 网壳模型Fig.4 Shell model
节点弹簧的轴向刚度和转动刚度分别根据欧洲木结构规范[10]计算,单个螺栓的轴向刚度由式(1)得出

式中,Kser为单个螺栓的滑移刚度(N/mm);ρm为木材密度,取500 kg/m3;d为销直径(mm)。
销直径取20 mm,结合螺栓及受剪面数量得到节点的轴向刚度为400 kN/mm,转动刚度为2.23×104kN·m/rad。胶合木材性见表1,钢材弹性模量取210 000 MPa,泊松比取0.3。

表1 木材力学参数Table 1 Mechanical parameters of timber
2 有限元分析结果
2.1 静力分析结果
对模型进行全跨活荷载工况下的静力分析,活载标准值取0.5 kN/m2,恒载标准值取1 kN/m2,并将面荷载设计值等效为节点荷载施加。
图5为S100与S100s模型第一扇区胶合木杆件的轴向应力对比图,可以看到,考虑节点域轴向滑移刚度后杆件轴向应力变化不明显。图6为网壳第一扇区胶合木杆件的弯曲应力对比图,可以看到,考虑节点轴向滑移刚度后各杆件应力分布基本一致,但杆件最大弯曲应力变化明显,由0.71 MPa增加到1.32 MPa。此处S100模型杆件的弯曲应力与轴向应力的比值为1∶1.79,而S100s模型对应杆件弯压应力比为1∶3.37,可见考虑节点轴向滑移刚度后,节点轴向压缩造成整体网壳竖向变形增加,杆件受力由轴向应力为主部分转化为以弯曲应力为主。
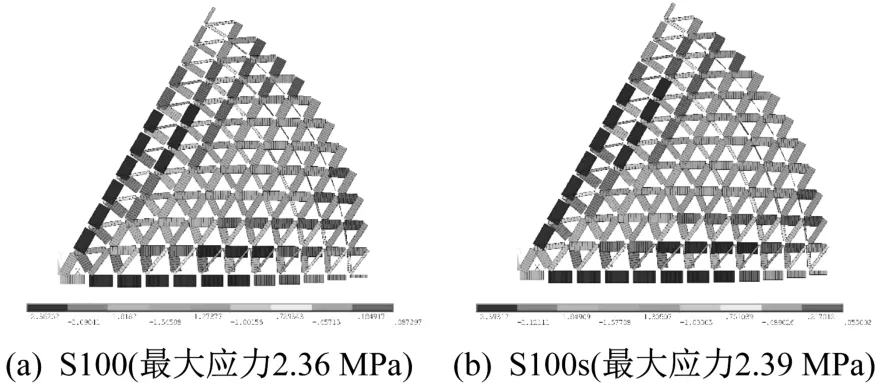
图5 网壳胶合木杆件轴向应力Fig.5 Axial stress of timber members
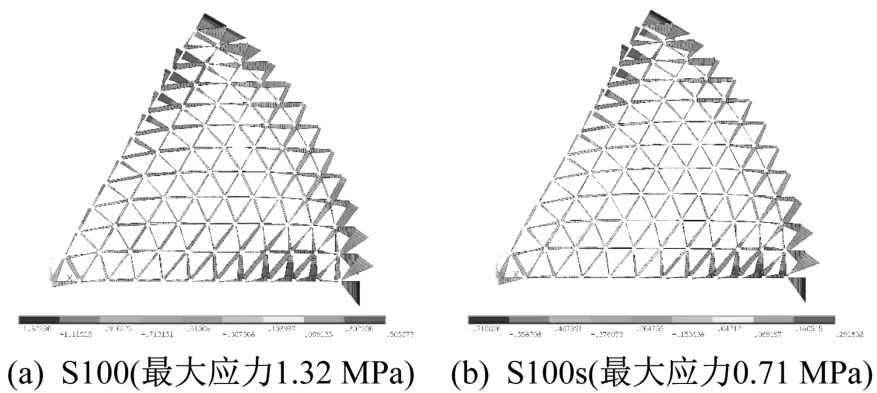
图6 网壳胶合木杆件弯曲应力Fig.6 Bending stress of timber members
对比模型的跨中挠度发现,在不考虑节点轴向滑移刚度时,模型的跨中挠度仅为8.27 mm;而考虑节点轴向滑移刚度后,模型跨中挠度增加到20.97 mm。可见,节点轴向滑移刚度对网壳竖向挠度影响较大,工程实践中应采取可靠措施限制节点轴向滑移,避免网壳实际变形因节点滑移超过理论值造成安全隐患。
2.2 网壳稳定承载力
对两种模型进行全过程稳定承载力有限元分析,得到两者的屈曲模态,如图7所示。可以看到,S100与S100s均发生对称分布的局部屈曲,S100模型的最大位移出现在网壳的第七环,S100s模型的最大位移位置出现在网壳的第五环。两者的失稳模态存在一定差别,S100模型主要表现为六环与七环之间的径向杆联合沉陷,而S100s模型发生五环上节点的局部沉陷。可以推测,由于径向杆所受轴力较大,节点轴向变形相比环向杆件更加明显,使得考虑节点轴向滑移因素后径向杆处节点易发生局部联合失稳。
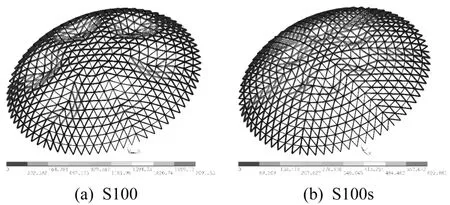
图7 网壳屈曲变形情况Fig.7 Buckling deformation of models
提取各模型位移最大节点处的荷载-位移曲线,以曲线中第一个临界点位置所对应荷载作为模型的稳定极限承载力。图8为两组模型的荷载-位移曲线图,可以看到,S100模型的极限承载力为19.36 kN/m2,S100s的极限承载力为 31.71 kN/m2,考虑节点轴向滑移后,S100模型承载力较S100s模型降低了38.9%。可见,木网壳节点轴向滑移刚度不仅改变网壳屈服破坏模式,还会对网壳的极限承载力产生较大影响。
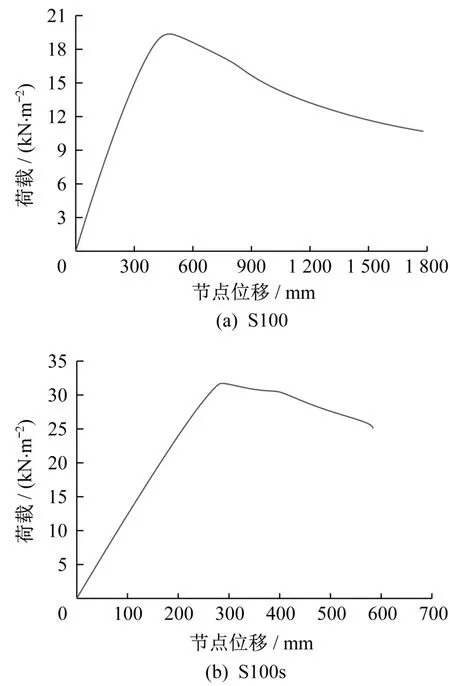
图8 模型荷载-位移曲线Fig.8 Load-displacement curves of models
3 既定跨度网壳的轴向滑移刚度影响分析
在上述S100模型的基础上,改变杆端与钢榖之间的间隙以及连接节点轴向滑移刚度,分析各因素对网壳稳定承载力的影响。
3.1 杆端间隙的影响
实际工程中,网壳杆件端部与钢毂表面很难密实接触,通常存在一定的间隙。为分析杆端间隙对网壳稳定承载力的影响,假定杆端存在2 mm、5 mm、10 mm间隙,开展有限元分析。通过对连接节点处轴向弹簧实常数定义为按接触前、接触后的两折线模型,模拟不同间隙的情况。以5 mm间隙为例,定义弹簧在变形小于5 mm时的轴向刚度为400 kN/mm,即按群栓滑移刚度考虑节点轴向刚度,认为杆件端部与钢毂无接触,内力完全通过群栓传至钢毂;而当弹簧5 mm外轴向刚度为1.34×105kN/mm,即木杆件全截面受压变形时的轴向刚度,此时杆件端部已与钢毂充分接触。
经分析,模型考虑不同杆端间隙后屈曲模态形态基本无变化,仅对结构整体刚度及极限承载力有一定影响。图9为各模型的荷载-位移曲线图,图中0 mm间隙为不考虑轴向滑移刚度模型,对应S100s模型;∞mm间隙为考虑轴向滑移刚度模型,对应S100模型。可以看到,当间隙为10 mm时,模型的荷载-位移曲线已与S100模型完全一致。对比间隙为2 mm和5 mm的模型发现,模型后期刚度随间隙的增加而降低,预期是由于部分杆件在加载过程中与钢毂接触,促使结构刚度得到提升。图10为各模型稳定承载力与杆端间隙的关系曲线,可以看出,随着间隙的增大,网壳稳定承载力明显下降,对应间隙为0 mm、2 mm、5 mm和10 mm时的网壳稳定承载力分别为31.62 kN/m2、27.03 kN/m2、22.03 kN/m2和19.34 kN/m2。可见,实际工程中,应严格控制杆件端部的连接间隙,做到压平顶实,可减缓节点滑移刚度对网壳承载力的影响。
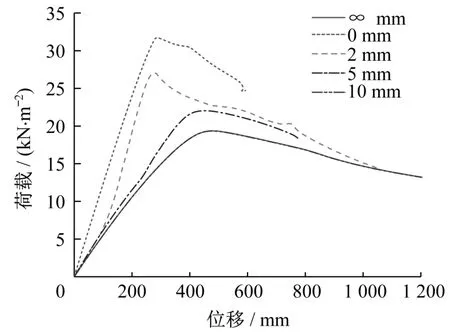
图9 荷载-位移曲线Fig.9 Load-displacement curves
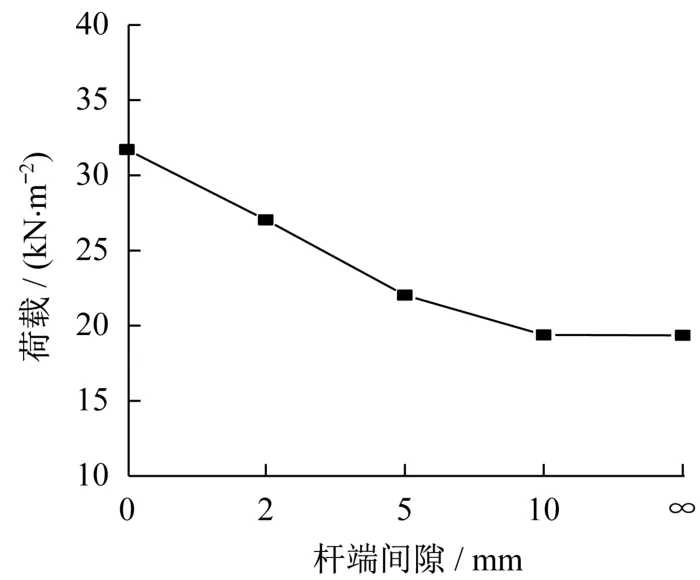
图10 稳定承载力对比Fig.10 Comparison of stability capacity
3.2 轴向滑移刚度的影响
结合工程中节点处螺栓的常见布置方式,以及与S100模型形成对比,以S100模型的轴向滑移刚度400 kN/mm为基准,考虑0.5倍、2倍、4倍、8倍的关系,节点刚度分别取200 kN/mm、800 kN/mm、1 600 kN/mm、3 200 kN/mm四种情况,分析节点轴向滑移刚度对木网壳稳定承载力的影响。
经计算,轴向滑移刚度为200kN/mm、800kN/mm的模型屈曲模态与S100模型基本一致,均为径杆中间环节点的局部沉陷,而轴向滑移刚度为1 600 kN/mm、3 200 kN/mm的模型屈曲模态首先为径杆中间环节点的局部沉陷,随后发生五环各扇区内节点的局部沉陷,与不考虑节点轴向滑移刚度的S100s模型基本一致。可见,随着节点轴向滑移刚度的增大,模型屈曲模态逐渐接近无节点轴向滑移网壳的情况,受节点刚度的影响逐渐降低。图11和图12为考虑不同节点轴向滑移刚度模型的荷载-位移曲线及各模型的稳定承载力对比图。可见,随着节点轴向滑移刚度的增加,网壳的稳定承载力随之增加,但提升的趋势逐渐变缓。木网壳的稳定承载力受节点的轴向滑移影响很大,且对于钢板螺栓节点,其轴向滑移刚度均位于影响程度较大的区间,实际工程中应对其节点刚度进行准确评估以得到网壳可靠的稳定承载力。
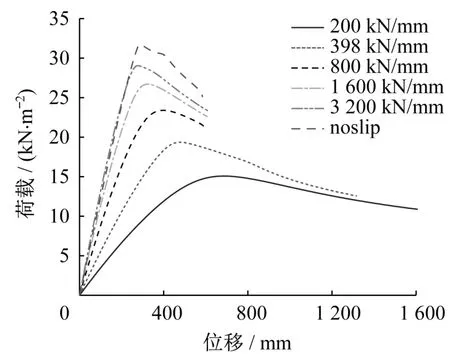
图11 荷载-位移曲线Fig.11 Load-displacement curves
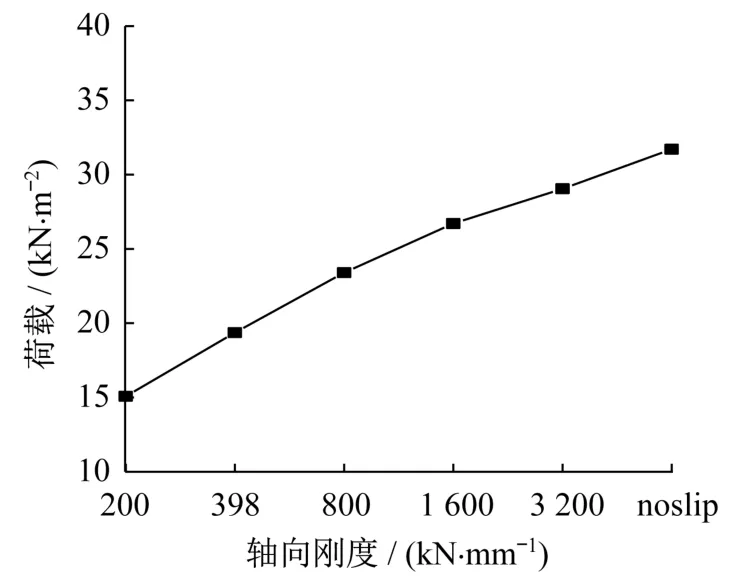
图12 稳定承载力对比Fig.12 Comparison of stability capacity
4 轴向滑移刚度对网壳影响的参数化分析
4.1 对不同跨度网壳的影响分析
对跨度为80 m和120 m的网壳分别进行分析,网壳的屈曲模态见图13,分别定义为S80与S120,同时定义S80s、S120s表示节点无轴向滑移的对比模型。可以看出,S80网壳的失稳模态与跨度100 m的S100模型基本相近。而S120网壳模型发生径杆处节点的局部失稳,但无节点轴向滑移的S120s模型的失稳点存在向环向外侧移动的趋势,S120s模型的屈曲形态较S100s模型也存在一定变化。可见,节点的轴向滑移刚度对不同跨度的网壳屈曲模态影响不同。
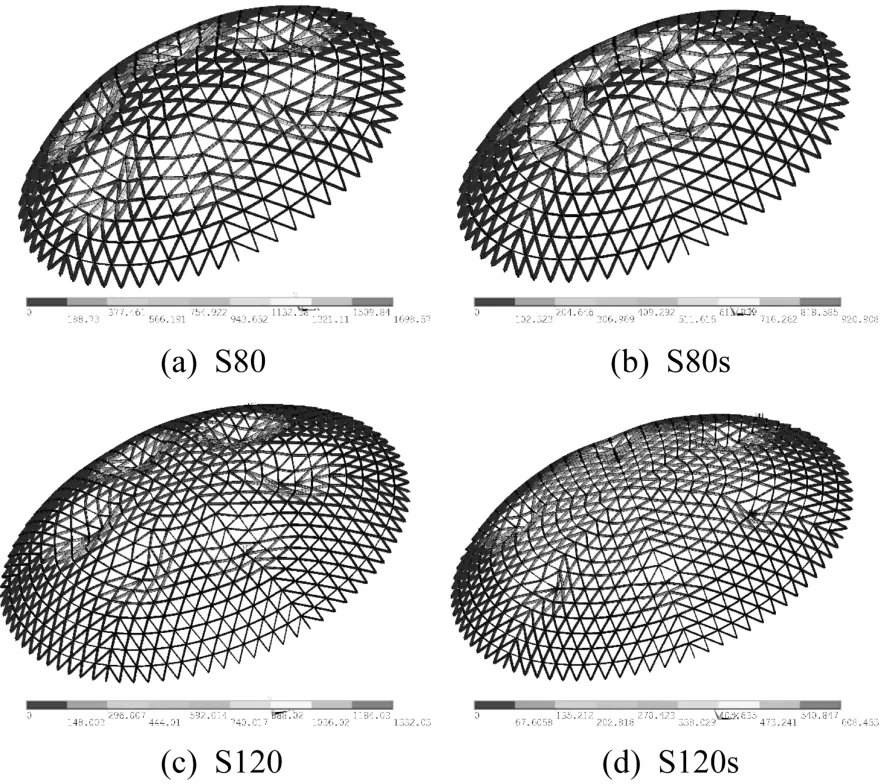
图13 网壳屈曲变形情况Fig.13 Buckling deformation of models
图14对应各组模型的荷载-位移曲线,可以看到,考虑节点轴向滑移刚度时,各组网壳的稳定承载力均显著降低。图15为各组模型稳定承载力的对比图,noslip和slip分别代表未考虑及考虑轴向刚度的模型,S80、S100、S120模型的稳定承载力在考虑节点轴向刚度后分别下降35.0%、38.9%和40.0%,可见,随着网壳跨度的增加,节点轴向滑移刚度对承载力的影响呈微弱增长的趋势。
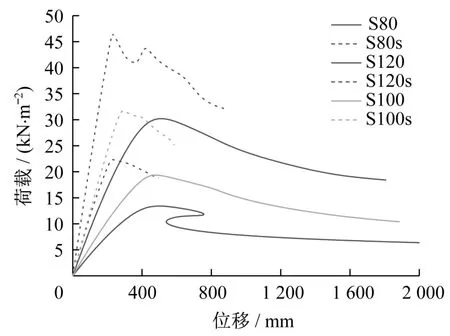
图14 荷载-位移曲线Fig.14 Load-displacement curves
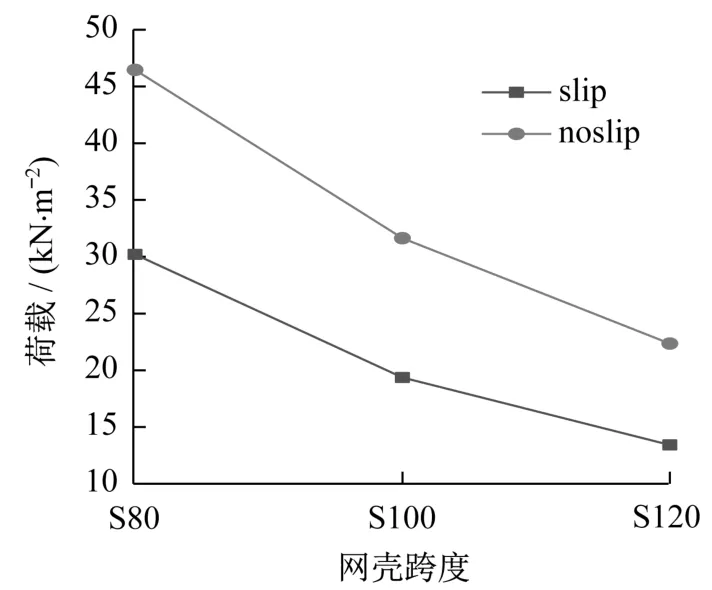
图15 稳定承载力对比Fig.15 Comparison of stability capacity
4.2 对不同矢跨比网壳的影响分析
对矢跨比分别为1/4和1/8的网壳进行分析,并与矢跨比为1/5的S100及S100s模型进行比较,网壳的屈曲模态见图16。可以看出,矢跨比1/4的网壳S100f4屈曲模态与S100网壳接近(图16(a)),但对于未考虑节点轴向滑移刚度的模型S100f4s,轴力较S100s提高,部分杆件提前发生面外失稳(图16(b))。对于矢跨比1/8的网壳,S100f8及S100f8s均发生以径杆处第七环节点为中心的局部区域塌陷,其中考虑节点轴向滑移刚度后,S100f8的塌陷区域更显著。可见,矢跨比降低后,节点轴向滑移刚度对网壳的屈曲模态影响不大,但存在加剧模型屈曲变形的趋势。
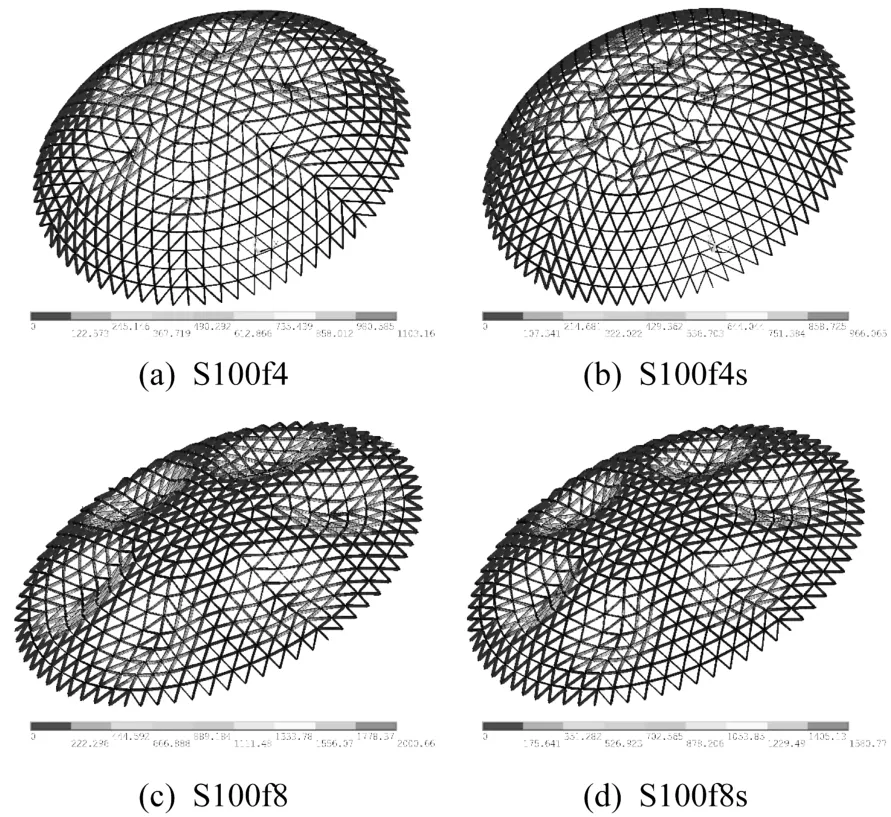
图16 网壳屈曲变形情况Fig.16 Buckling deformation of models
图17和图18分别为各模型的荷载-位移曲线和各模型稳定承载力的对比图。可以看出,S100f4、S100、S100f8模型的稳定承载力在考虑节点轴向滑移刚度后分别下降22.5%、38.9%和38.4%。由图18可以看出,相比矢跨比为1/4、1/8的模型,矢跨比为1/5时节点轴向滑移刚度对木网壳稳定承载力的影响最大。由此可见,节点刚度对不同矢跨比网壳的影响,并非线性关系,而存在某一最不利的矢跨比情况。
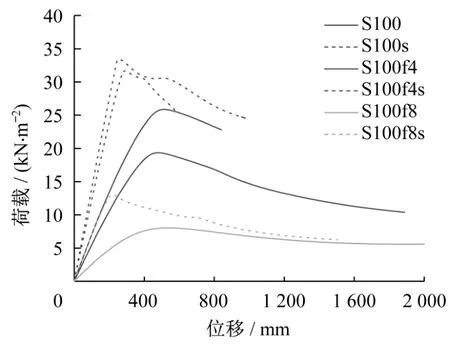
图17 荷载-位移曲线Fig.17 Load-displacement curves
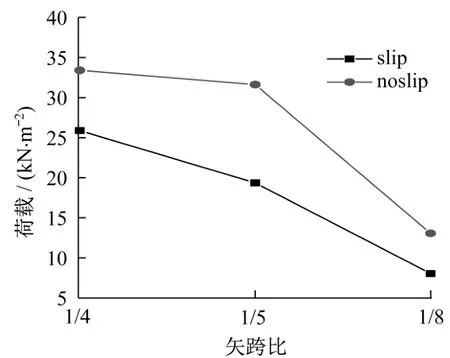
图18 稳定承载力对比Fig.18 Comparison of stability capacity
4.3 对不同分频数网壳的影响分析
对分频数为11和13的网壳进行分析,网壳的屈曲模态见图19。可以看出,对于分频数为11的网壳,S100P11模型发生径杆处第六、七环节点的局部塌陷,而分频数为13的网壳,S100P13模型发生径杆第七、八环节点的局部塌陷。可见,考虑节点轴向滑移刚度时,不同分频网壳的屈曲形态未发生明显变化。不考虑节点轴向滑移刚度时,不同分频数的S100P11s和S100P13s模型均发生扇区内第四环处节点的局部区域沉陷,但区别在于,S100P13s模型径杆处节点随后也发生沉陷,导致图示模型屈曲模态存在一定区别。

图19 网壳屈曲变形情况Fig.19 Buckling deformation of models
图20为各组模型的荷载-位移曲线,可以看出,不同分频数对未考虑节点轴向滑移刚度模型(S100P11s,S100P13s)的稳定承载力影响较大,而对考虑轴向滑移刚度模型的影响程度反而不明显。图21为各模型稳定承载力的对比图,可以看出,考虑轴向滑移刚度后模型S100P11、S100P13随着分频数的增加,节点轴向刚度对木网壳稳定承载力的影响略微变小;S100P11、S100、S100P13模型的稳定承载力在考虑节点轴向刚度后相对不考虑节点轴向刚度分别下降26.2%、38.9%和41.7%。可见,节点轴向滑移刚度在分频数较多的网壳中影响更加明显,主要是由于分频数的增加,整体节点数量随之增加,进而增加了节点轴向滑移刚度的影响程度。
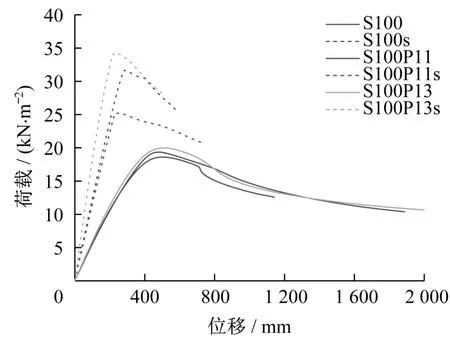
图20 荷载-位移曲线Fig.20 Load-displacement curves
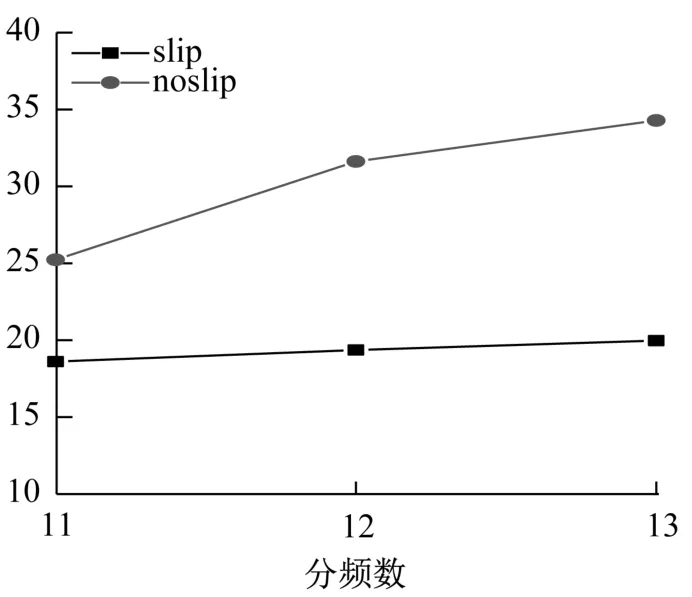
图21 稳定承载力对比Fig.21 Comparison of stability capacity
4.4 对不同荷载作用方式网壳的影响分析
分别对半跨及1/3区域施加活荷载的网壳进行分析,网壳的屈曲模态见图22。可以看出,各模型均发生荷载作用区域部分节点的局部塌陷。对于半跨加载的网壳S100L1与S100L1s,均发生加载区域靠近中部扇区内第二环节点的局部塌陷,但考虑节点轴向滑移刚度的S100L1模型塌陷程度较大,与三环及四环节点形成联合塌陷。对于1/3区域加载的网壳S100L2与S100L2s,发生加载区域中间径杆二、三环节点的局部塌陷,同样考虑节点轴向滑移刚度模型S100L2的沉陷区域更大。可见,在不均匀加载情况下,节点轴向滑移刚度对网壳的屈曲变形的分布基本无影响,仅会加剧模型屈曲变形的程度。
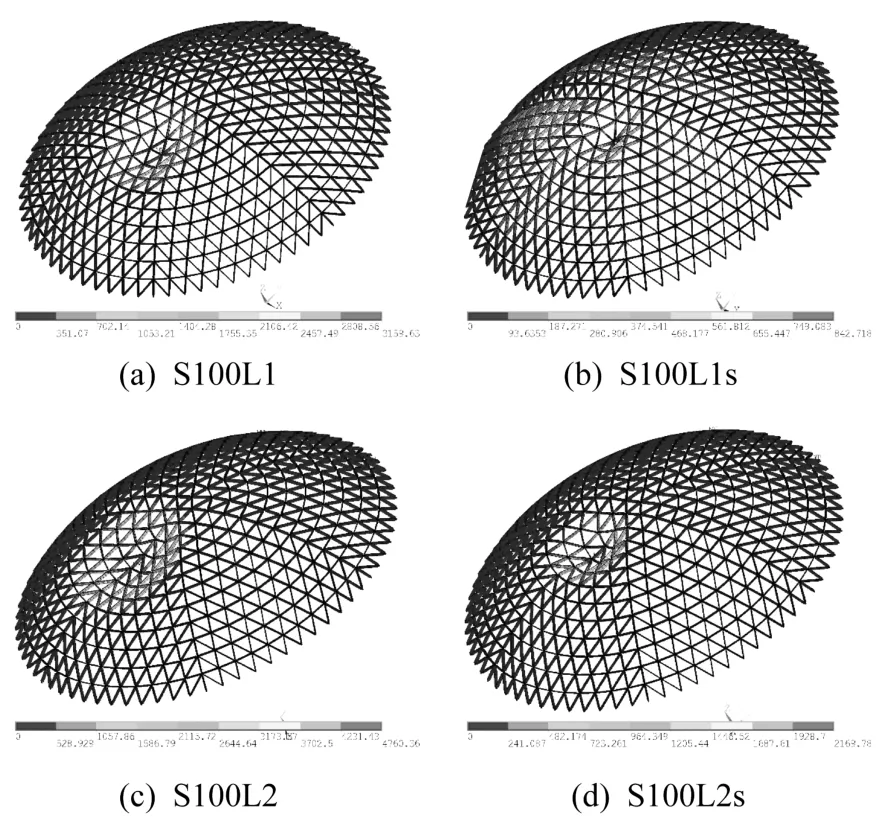
图22 网壳屈曲变形情况Fig.22 Buckling deformation of models
图23和图24分别为各组模型的荷载-位移曲线及稳定承载力的对比图。可以看出,局部受荷对木网壳的稳定承载力不利。此外,由于节点塌陷位置的不同,各模型在达到稳定承载力时对应的节点变形有一定的区别,满跨作用荷载时节点的变形相对较小。S100、S100L1、S100L2模型的稳定承载力在考虑节点轴向滑移刚度后分别下降38.9%、34.0%和36.0%。可见,虽然荷载分布不同,节点轴向滑移刚度对各网壳模型的承载力削弱程度接近。
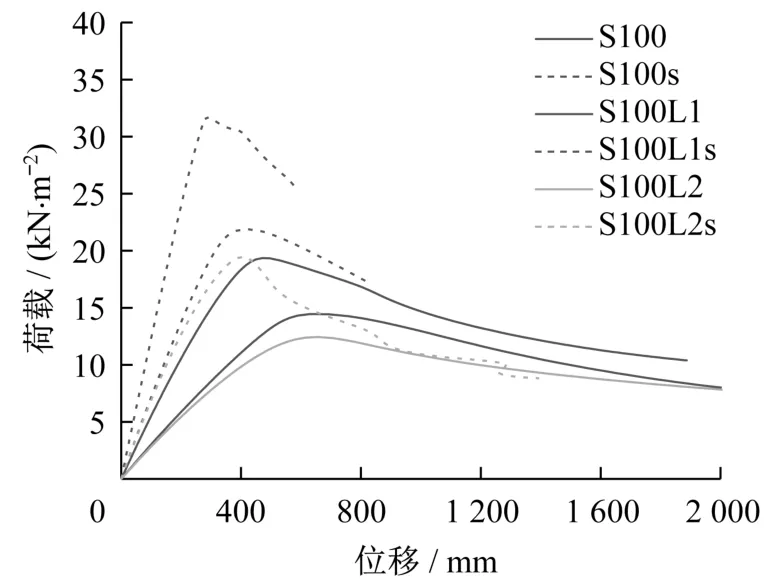
图23 荷载-位移曲线Fig.23 Load-displacement curves
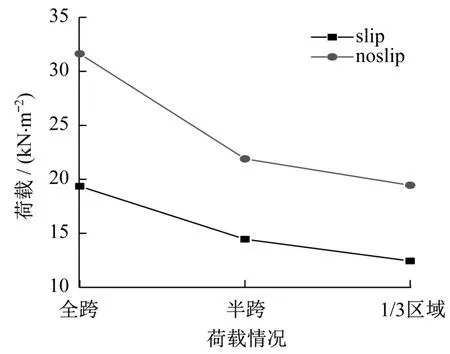
图24 稳定承载力对比Fig.24 Comparison of stability capacity
5 结 论
本文基于APDL语言建立了考虑不同参数的有限元模型,分析节点轴向滑移刚度对钢板-螺栓节点木网壳稳定承载力的影响。具体结论如下:
(1)采用Combin39非线性弹簧单元可同时模拟木网壳节点的轴向以及转动刚度特性。考虑节点轴向滑移变形后,网壳整体竖向挠度增加,部分杆件由轴压受力转化为弯曲受力为主;考虑节点轴向滑移刚度后,网壳的杆件内力、变形发生一定程度的改变,从而影响到网壳的破坏模式及极限承载力。
(2)随着杆端与钢毂之间的间隙增大,钢板-螺栓节点木网壳的稳定承载力明显下降,当间隙超过10 mm时,钢毂对节点的轴向滑移变形几乎无约束,轴向滑移刚度对网壳的不利影响将充分发挥。实际工程中,应提高节点加工与安装精度,或采用可靠措施限制节点的轴向滑移变形。
(3)随着网壳跨度的增加,节点轴向滑移刚度的不利影响呈增长较慢;既定节点滑移刚度对不同矢跨比网壳的影响,呈现非线性关系,存在最不利矢跨比情况。矢跨比降低后,节点轴向滑移刚度对网壳的屈曲模态影响减弱,但会加大网壳屈曲变形的程度。
(4)随着网壳分频数的增加,网壳节点数量随之增加,造成节点轴向滑移刚度在分频数大的网壳中影响更加明显。
