基于EWMA-kNN的多工况过程微小故障检测

郭小萍，徐 月，李 元

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

随着现代工业过程生产规模不断扩大，企业生产系统的自动化水平和集成化程度也在不断提高，生产单元之间的高关联性使得过程故障具有了比以往更强的破坏性.为了减少故障造成的影响，基于数据驱动的故障检测方法受到了广泛关注[1-2].近年来，在解决具有非线性、多工况等方面特征的工业过程故障检测取得了很多成果.其中主元分析(principal component analysis，PCA)和kNN在故障检测方面得到了广泛应用[3-7].

PCA方法假设数据服从多元高斯分布，但是由于实际工业生产过程的复杂性和多样性，数据很难满足这种假设，这使得PCA在处理非线性和多模态数据时有一定的局限性[8-10].Bakdi等[11]提出一种自适应PCA的方法，使用改进EWMA算法更新控制限，提高PCA方法的检测性能.He等[12]提出了FD-kNN(Fault detection based onk-nearest neighbor)故障检测方法.该方法依据正常样本相似、距离较近，而大多数故障样本与正常样本距离较远的特点，通过计算两个样本间的欧式距离，寻找样本的k个近邻，使用k个近邻的距离平方和作为故障检测统计量，可以相对有效地解决非线性和多模态的问题.在此基础上，Verdier等[13]提出了基于马氏距离的FD-kNN故障检测方法.该方法使用马氏距离代替欧氏距离，通过样本的局部近邻估计得到协方差矩阵，改善了故障检测结果.He等[14]提出了基于主成分的kNN(principal component based onkNN，PC-kNN)故障检测方法，解决了FD-kNN建模和监测时计算量大的问题.但是，PC-kNN方法只使用了主元空间中的信息，忽略了残差空间中可能有用的信息.郭小萍等[15]提出了特征空间kNN故障检测，该方法将得分矩阵和SPE统计量进行组合，构建特征空间.在特征空间中既包含主元空间信息又包含残差空间信息，从而使故障检测效果更精确.

此外，当多工况过程发生微小故障时，因其微小故障样本与正常样本距离较近，FD-kNN方法很难检测出故障样本.EWMA方法可以用来检测缓慢漂移和微小变化[16-17].因此，本文提出一种EWMA-kNN故障检测方法，将改进EWMA与kNN方法结合，以解决FD-kNN方法在多工况过程故障检测时微小故障样本较难被检测的问题.利用k近邻方法计算训练数据样本间的欧氏距离，构建故障检测统计量，并利用核概率密度估计方法确定相应的控制限Dlim.在监视过程中，首先寻找测试数据的近邻；然后使用改进的指数加权移动平均算法确定相应时刻的控制限Dnew(i)；最后通过一个多模态数值例子和半导体生产过程进行故障检测仿真实验.仿真结果表明了该方法的有效性.

1 kNN算法

kNN的基本思想是使用样本和其近邻的距离来度量样本的差异[18].假设有训练数据Xm×n，其中：m为训练数据的样本数量；n为训练数据的变量数量.在训练集中寻找样本xi的前k个近邻，分别为x1,x2,x3,…,xk，并计算样本xi的前k个距离的平方和作为故障检测统计量，记为

(1)

其中d(xi,xj)2=‖xi-xj‖2，j=1,2,…,k，且j≠i.最后，利用概率密度估计法(KDE)确定控制限，记为Dlim.

2 EWMA-kNN多工况过程故障检测方法

2.1 改进指数加权引动平均(EWMA)算法

设第i个样本的检测统计量为d(xi)，控制限为Dnew(i).

[cd(xi-w+1)+c2d(xi-w+2)+…+

(2)

其中:c为权重指数(>1),c越小，权重越大；w为窗口长度.当故障发生时，d(xi)>Dlim，代入公式(2)得：

(3)

令新的控制限为

(4)

随着时间的增加，故障的累积会越来越多，等式右侧的第二部分越来越大，从而控制限会降低，有利于微小故障的检测.但是对于某些故障，一旦控制限降为零或负数时，以后的所有数据都将被认为是故障数据.同时，考虑到要降低误报率和提高检测率,所以，使自适应控制限高于或等于固定控制限的一半[11]:

(5)

2.2 EWMA-kNN故障检测

本文EWMA-kNN故障检测方法分为离线建模和过程监视两部分，故障检测流程图如图1所示.

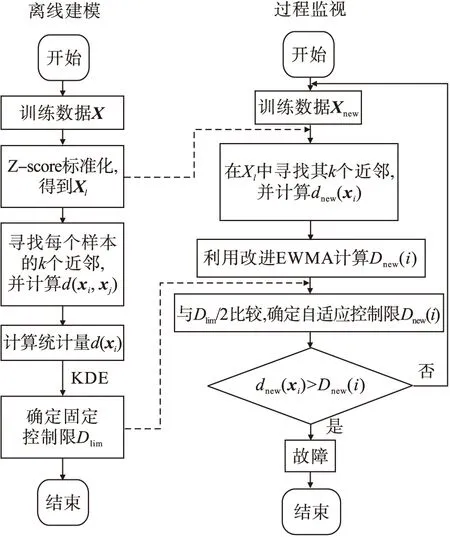
图1 EWMA-kNN故障检测流程Fig.1 Fault detection flow of EWMA-kNN

2.2.1 离线建模

建立故障检测模型的主要步骤：

(1) 选取训练数据X，使用Z-score[19]进行标准化，得到Xl；

(2) 在Xl中寻找每个样本的k个近邻，计算d(xi,xj),j=1,2,…,k；

(3) 计算故障检测统计量d(xi)，确定置信度为95%的固定控制限Dlim.

2.2.2 过程监视

过程监视的主要步骤：

(1) 获取测试数据Xnew，使用建模时的均值和标准差对其进行标准化，得到Xnewl；

(2) 在Xl中寻找每个测试样本的k个近邻，计算dnew(xi,xj),j=1,2,…,k；

(3) 计算统计量dnew(xi)；

(4) 采用公式(6)确定自适应控制限Dnew(i)；

(5) 将dnew(xi)与Dnew(i)进行比较，确定检测结果.

3 仿真研究

3.1 数值案例

以Ge和Song[20]设计的数值例子为例.该例子包含5个变量，由以下模型产生两个模态的数据，其中e1、e2、e3、e4和e5是服从[0，0.01]的白噪声.

(6)

模态1：s1∈U(-10,-7)，s2∈N(-15,1).

模态2：s1∈U(2,5)，s2∈N(1,7).

每个模态采集400个样本，组成训练数据；再在每个模态采集800个样本，组成测试数据.在采集模态1测试数据时，变量5从401个样本开始加入幅值为1.2的故障.同样，在采集模态2测试数据时，变量5从401个样本开始加入幅值为0.02*(i-400),i=401,402,…,800的故障.图2为测试数据在前3个主元上的投影.从图2可以看出：数据明显分为两个模型，模型1和模型2中均有部分故障样本接近正常样本.

图2 测试数据在前3个主元上的投影Fig.2 Projection of test data on the first three principal elements

使用本文所提方法EWMA-kNN、PCA和kNN方法分别进行故障检测.主元个数由方差累计贡献率确定，其余参数可由交叉验证法[21]得到.本节中主元个数是1，k=3，c=1.2，w=10.

图3和图4分别是MPCA-T2和MPCA-SPE故障检测效果图.从图3和图4可以看出：PCA对于故障的检测效果并不理想，尤其是T2的检测结果，对于模型2的故障均没有检测出来.

图3 MPCA-T2故障检测效果Fig.3 Fault detection of MPCA-T2

图4 MPCA-SPE故障检测效果Fig.4 Fault detection of MPCA-SPE

图5是FD-kNN故障检测效果图.从图5可以看出:kNN方法对于接近正常样本的故障检测效果不理想，并且存在较多的误报现象.图6是EWMA-kNN故障检测效果图.从图6可以看出：EWMA-kNN方法可以检测出绝大部分故障且误报较少.

检测率(DR)和误报率(FAR)的计算方法[21]如式(7)和(8)所示：

(7)

(8)

其中:NF为故障数据的数量;NF,f为故障数据中被检测为故障的数量;NN为正常数据的数量;NN,f为正常数据中被检测为故障的数量.

图5 FD-kNN故障检测效果Fig.5 Fault detection of FD-kNN

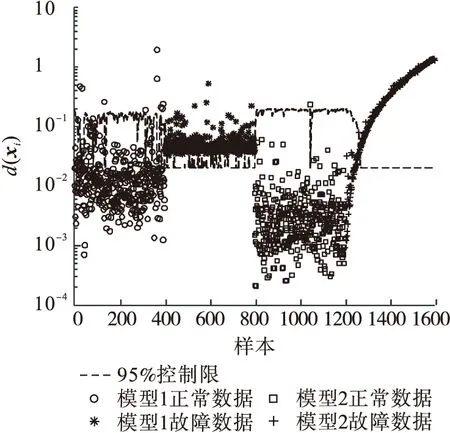
图6 EWMA-kNN故障检测效果Fig.6 Fault detection of EWMA-kNN

表1为各方法故障检测结果统计.从表1中看出：EWMA-kNN的故障检测率为91%，误报率为2.625%；FD-kNN的故障检测率为77.625%，误报率为5.25%；PCA方法的检测结果明显不如其他两种方法.三种方法相比，EWMA-kNN故障检测方法明显优于PCA和FD-kNN方法，证明本文所提方法改善了FD-kNN对于近似于正常样本的故障的检测效果.

表1 故障检测结果统计Table 1 Statistics of fault detection results

3.2 半导体生产过程仿真实验

半导体生产过程是典型的时变和多工况的批次生产过程[22-24].美国德州仪器公司半导体生产过程的实际数据常被用于验证间歇过程检测算法的有效性.该数据集一共有129批次，包括108批次的正常数据和21批次的故障数据，其中故障数据可以通过改变过程压力和RF功率等参数得到. 这些数据通过3个不同的实验获得，每个过程包括40个测量变量.本研究选取17个变量.因为有两个批次的数据缺失，所以选取107批次的正常数据和20批次的故障数据.使用最短时间法处理批次过程中数据不等长的问题.提取每个批次数据的第6至第90时刻的数据，因此参与仿真实验的正常数据和故障数据可以分别表示为(107×17×85)和(20×17×85)，按批次方向展开后分别表示为(107×1445)和(20×1445).

随机选取95批次的数据作为训练数据，32批次数据作为测试数据.在测试数据中包括12批次正常数据和20批次故障数据.使用MPCA方法对127 批次数据进行分析，样本在前3个主元上的散点图如图7所示.从图7中可以明显看出：所有数据分为3类，而且在不同角度下，故障3和故障9距离正常批次都较近.

图7 数据在前3主元上的散点Fig.7 Scatter of data on the first three principal elements

采用MPCA方法进行故障检测，根据方差累积贡献率法确定主元个数为3.故障检测效果如图8和图9所示.从图8可以看出：MPCA-T2检测出6批次故障，且误报了5批次.从图9可以看出：MPCA-SPE能够检测出17 批次故障，同样有5批次的误报.综合考虑，MPCA方法能够检测出17批次的故障且存在误报现象.

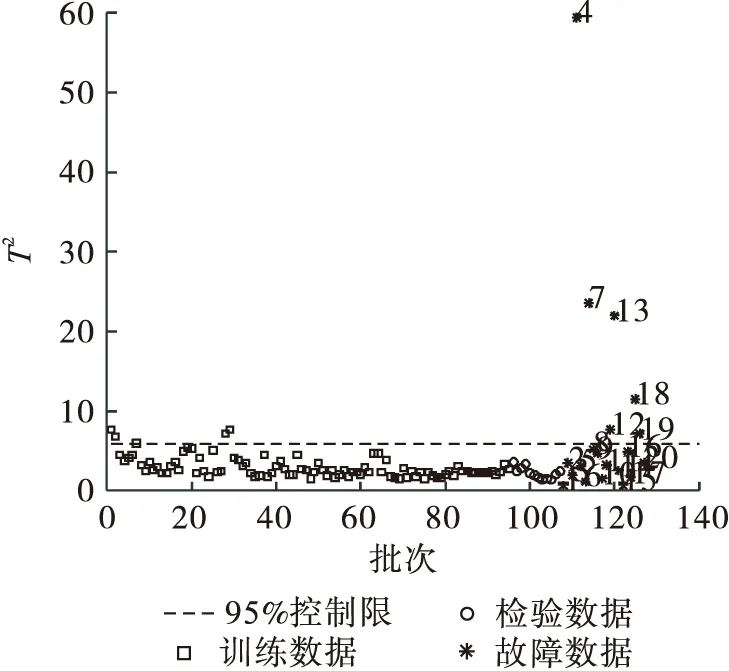
图8 MPCA-T2故障检测效果Fig.8 Fault detection of MPCA-T2

图9 MPCA-SPE故障检测效果Fig.9 Fault detection of MPCA-T2

采用FD-kNN和EWMA-kNN方法进行故障检测，如图10和图11所示.根据交叉验证法确定近邻个数为5，c=2,w=20.从图10可以看出：FD-kNN方法检测效果与MPCA-SPE检测效果相似，能够检测出16批次故障，且存在1批次误报现象.故障3和故障9均没有被检测出来.从图11可以看出：EWMA-kNN方法能够检测出所有故障，并且没有误报.与其他几种方法相比，故障检测效果有明显提高，验证了本文所提方法的有效性.

图10 FD-kNN故障检测效果Fig.10 Fault detection of FD-kNN

图11 EWMA-kNN故障检测效果Fig.11 Fault detection of EWMA-kNN

表2为半导体生产过程故障检测结果统计.从表2中可以看出：MPCA方法能够检测出17个故障，故障3、5和6没有被检测出来；FD-kNN方法共检测出16个故障，4个故障没有被检测出来，其中包括故障3和9；EWMA-kNN方法将20个故障全部检测出来，说明EWMA-kNN方法能够检测出多模态中与正常数据相近的故障，证明了该方法的有效性.

表2 半导体生产过程故障检测结果统计Table 2 Fault detection results statistics of semiconductor manufacturing process

4 结 论

本研究针对多工况过程发生微小故障时，kNN方法检测效果不理想的问题，提出了EWMA-kNN故障检测方法.在建立离线故障检测模型时，使用FD-kNN方法确定相应检测控制限.过程监视时，利用改进EWMA方法更新控制限.该方法有效地改善了故障检测效果，降低了误报率，同时提高了检测率.本文通过多模态的数值案例和半导体生产过程的仿真研究结果分析得知：EWMA-kNN方法提高了kNN方法的故障检测性能，有效检测到过程中的故障，证实了EWMA-kNN方法的有效性.目前该方法针对小样本数据集有明显效果，当应用于大规模数据集时，尤其是包含变量维度高且大量不相关的大数据集时，可能会出现运算速度慢、距离测量度变得不可靠等问题，使得模型的检测效果下降，下一步将针对大数据集进行研究.