超空间上的MCM,K-MCM空间和函数插入
2021-02-10胡星宇肖经渊彭良雪
胡星宇,肖经渊,彭良雪
(1. 北京工业大学 理学部,北京 100124;2. 广州工商学院 通识教育学院,广东 广州 510850)
自1983年MASHHOUR[1]给出超拓扑空间的定义以来,超空间上的各种性质就被广泛研究.如:张国芳[2]在超拓扑空间上引入超可数紧空间、超仿紧空间[3],研究了它们的若干性质,给出了超半连续函数的概念,并且利用这些概念给出了超可数紧空间的一些刻画[4];DEVI等[5]引入了超α开集,并探讨了它的相关性质;SAYED[6]引入了一个新的集合类,把它命名为超b开集,利用它给出了超b开(闭)映射的概念,并讨论了它们之间的关系;MUSTAFA[7]研究了超拓扑空间中的弱分离性;AL-SHAMI[8]研究了超拓扑空间中特殊的一些超覆盖和超分离公理;在文献[9-10]中,AL-SHAMI继续引入了超α紧性,几乎超α紧性,以及弱超α紧性等相关概念,并且研究了它们之间的关系;张国芳[11-13]研究了超拓扑空间上超星覆盖的若干性质,超拓扑空间上的可乘性质和相对超分离公理.
近年来,一般拓扑空间上的函数插入问题受到广泛的关注,尤其是某些广义度量空间和函数插入的关系更是被深入研究.如:燕鹏飞[14]得到了半层空间、K-半层空间和函数插入之间的关系;谢利红[15]通过研究单调递减的集合列,给出了可数亚紧、可数仿紧、完全正规空间和函数插入之间的关系.受此启发,本文尝试在超空间中对某些广义度量空间进行研究,讨论它们和函数插入之间的关系.
1 基本概念
定义1[3]若X上的子集族μ满足μ包含X和∅并且μ的任意子族的并仍在μ中,则称μ为X上的超拓扑,偶对 ),(μX称为超拓扑空间μ中的元素叫做超开集,超开集的补集叫做超闭集.
定义 2[3]设(X,μ)是一个超拓扑空间,x∈X,如果U是X的一个子集,存在一个超开集μ∈V,使得x∈V⊂U,则称U是点x的一个超邻域.
定义3[3]设E是超空间(X,μ)的一个子集,那么包含E的所有超开集的交叫作E的超闭包,记作scl(E) .
定义4[3]在超拓扑空间 (X,μ)中,若每一个超闭子集F和每一点Fx∈,都存在2个不相交的超开集G、H分别包含F、x,则称X是超正则空间,也称X是 3ST空间.
定义5[3]一个超拓扑空间 (X,μ),若2个不相交的超闭集F1和F2,存在不相交的超开集G和H分别包含F1和F2,则称超拓扑空间 (X,μ)是超正规空间,也称X是 ST4空间.
定义6[4]设 (X,μ)是超拓扑空间,是赋予通常拓扑的实直线.f:X→是超上半连续函数(超下半连续函数),若对任意r∈,集合{x∈X:f(x)<r} (或 {x∈X:f(x)>r})是超开集.
定义7[2]定义一个超拓扑空间),(μX,若对于X的任意超开覆盖均有一个有限的超子覆盖,则称它为超紧空间.
定义8[16]空间X被称作单调可数亚紧空间MCM,如果存在一个算子S,将X中的每一个相交为空集的递减的闭集列{Fn}都对应X的超开集列S(n, {Fn})),并且满足:

定义 9[17]满足下述条件的空间X称为K-M C M空间:存在X上的g函数,使得对X的任一序列{xn}及紧集C,若对于任意n∈ω(ω代表自然数的基数),有则序列{xn}在X中有聚点.
文献[17]中称K-MCM空间为kβ空间.
定义10对于超拓扑空间 ),(μX,将X上的全体超下(上)半连续函数构成的集合记作CLSC(X)(CUSC)(X).
定义 11令{An}和{Bn}是超拓扑空间(X,μ)的2个超子集序列.为了简便,对于任意n∈,如果An⊂Bn,则把{An}和{Bn}的关系记作.此外,令
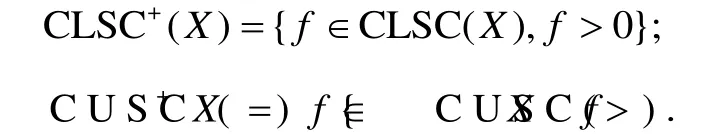
2 主要结果
首先给出C-MCM,C-K-MCM半层空间的概念.
定义12[18]空间X被称作单调超可数亚紧空间C-MCM,如果存在一个算子U,将X中的每一个相交为空集的递减的超闭集列{Fn}都对应X的超开集列U(n,{Fn})),并且满足:
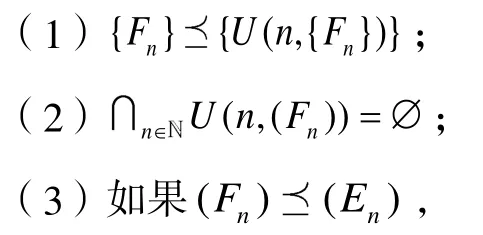
定义13[18]设X为超拓扑空间 ),(μX,函数g:是X上的超g函数,如果对于x∈X和n∈,有x∈g(n+1,x)⊂g(n,x)成立.
下面,利用超g函数和递减的超闭集列刻画C-K-M CM空间.
定义14[18]满足下述条件的超拓扑空间 ),(μX称为C-K-MCM空间:存在X上的超g函数,使得对X的任一序列{xn}及超紧空间K,如果对于任意n∈,都有成立,则序列{xn}在X中有聚点.
接下来讨论C-K-MCM空间性质,由文献[17]的定理4易得以下结论:
定理1设X为超拓扑空间(X,μ),则下列条件相互等价:
(1)X是C-K-MCM空间;
(2) 存在一个算子U,将X中的每一个相交为空集的递减的超闭集列{Fn}都对应为X的超开集列{U(n, {Fn})},使得下面这些结论成立.
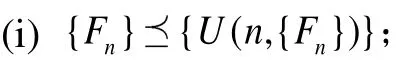
(ii) 对于X的任一超紧子集K,存在n∈,使得
如果算子U满足定义12或者定理1的条件,那么它被称作C-MCM算子或者C-K-MCM算子.
定理2设X是超拓扑空间(X,μ),则下列等价:
(1)X是C-MCM空间;
(2) 存在保序算子映射
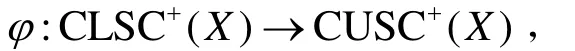
证明:(1) (2)⇒ . 根据定义12,假设算子U是X上的C-MCM算子.对于任意h∈ CLSC+, 令Fn(h) = {x:h(x) ≤ 1/n- 1},在这里n> 1, 并且F1(h) =X.那么{Fn(h) }是相交为空集的递减的超闭集列.当时,定义φ(h) :X→,并且φ(h)(x) = 1/n,所以
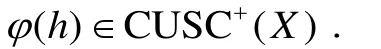
此外,对于任意大于0的实数r,都存在n∈,使 得是超开集.
现在假设h,h‘ ∈CLSC+(X),并且h≤h‘,因为h‘(x) ≤ 1/n-1,所以h(x) ≤ 1/n-1,所以,对于任意n∈,都有Fn(h‘ ) ⊂Fn(h)成立.那么,对于任意n∈,都有成立.
对于任意x∈X,存在n∈,使得

取定这些n,有成立,所以
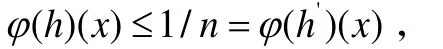
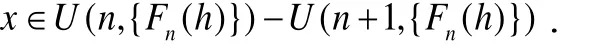
所以,φ(h)(x) = 1/n,并且因此h(x)> 1/n.综上所述,φ(h)<h.
(2) ⇒ (1).假设{Fn}是X中相交为空集的递减超闭子集序列,可以假设F1=X.当时,令h{Fn}:X→ [0,1],并且,因此
这足以证明U是X上的C-MCM算子,下面展开证明.
显而易见,每一个U(n,{Fn})都是超开集.因为x∈Fn,当且仅当h{Fn}(x)≤ 1/n,所以对于任意n∈,都有Fn⊂U(n,{Fn})成立.对于任意x∈X,都存在n∈,使得φ(h{Fn})(x) > 1/n.取定这些n,有成立,这意味着
现在假设{Fn}和 {Fn‘}是2个相交为空集的递减超闭子集序列,并且,那么所以,这意味着对于每一个n∈,都有成立.因此U是X上的C-MCM算子.证毕.
定理3设X是超拓扑空间 ),(μX,则下列结论等价:
(1)X是C-K-MCM空间;
(2) 存在保序算子映射φ: CLSC+(X) → CUSC+(X)满足以下条件:
(ii)对于X的每一个超紧子集K,对于所有的xK∈,都存在实数 0r>,使得φ(h)(x)>r.
证明:(1) (2)⇒ .根据定理1,假设U是X上的C-K-MCM算子,对于每一个令Fn(h) = {x:h(x) ≤ 1/n- 1},在这里n> 1,并且F1(h)=X.那么{Fn(h) }是相交为空集的递减的超闭集列.
现在令K是X的超紧子集,存在n∈,使得.令r= 1/n,根据φ(h)的定义,
对于所有的x∈K,都有φ(h) (x) >r成立.
(2) (1)⇒ .假设{ }nF是相交为空集的递减的超闭子集列.可以假设F1=X,当x∈Fn-Fn+1时,定义h{Fn}:X→ [0,1],并且h{Fn}(x) = 1/n成立.因此h{Fn}∈CLSC+(X).
再令

由定理2的证明可知,U是X上的C-MCM算子.
令K是X的超紧子集,存在 0r>,对于所有的x∈K,都有成立.
又因为一定存在n∈,使得1/n<r,取定这些n,有K∩U(n,{Fn})=∅成立.证毕.
