非遗与数学的结合

刘贝托 陈凤仪 陈岸瑛

2006年，苏绣入选第一批国家级非物质文化遗产，开启了传承的新篇章。经过15年的探索与实践，以苏绣为代表的中国刺绣类传统工艺，在传承创新与明确自我定位的道路上取得了很大进步。尤其是在传统技艺的影像化、数字化与产品创新等层面上，涌现出一批杰出的作品。然而，目前苏绣的发展仍然存在一个核心问题——对苏绣本体性的认识与创新深入程度较低。在面临针法传承断层，行业内卷以及发展方向模糊等诸多问题时，将数学语言与思维引入苏绣之中，利用拓扑学思维将具体的针线轨迹抽象成为函数模型，进而将针法转化为可交流的“语言”，既为解决上述难题提供了方法，也为苏绣针法的创新提供了可能性。

一、项目缘起——针法作为苏绣的艺术本体

针法和丝线配色是刺绣的基本艺术语言。苏绣在其发展过程中，集天下针法之大成，且与文人书画相融合，在艺术表达上高度精细复杂。近代以来，又受西洋绘画的影响，形成融通中西的绣画风格。

人们欣赏绣画，首先看到的是题材和形象。活灵活现地摹仿书画效果的确是苏绣的一大能事，但若仅仅停留于此，苏绣自身的艺术特色则难以凸显，进而使其艺术地位也将始终低于书画。对此，国家级非物质文化遗产项目苏绣传承人、中国刺绣艺术大师姚惠芬有较为自觉的意识，她与当代艺术家邬建安合作，以密集展现苏绣针法的创新作品参加第57届威尼斯双年展，凸显了绣画不同于绘画的艺术本体。

从沈寿到李娥英，前辈大师们总结苏绣针法、著书立说。至姚惠芬这一代，则与当代艺术相结合，揭示针法特有的艺术价值，寻觅苏绣（绣画）自我突破的契机[1]。

在西方现代主义艺术发展过程中，艺术本体语言得到了高度重视，其中一部分艺术家还将艺术形式与数学联系到一起，创作出纯抽象的作品。其后，纽约艺术家索尔·勒维特（Sol LeWitt， 1928–2007年）则进一步用数学公式生成概念艺术作品。

借鉴这一思路，我们可以追问这样一个问题：苏绣针法可否被数学化？在算法和人工智能技术突飞猛进的今天，这一问题不仅具有艺术史价值，而且具有实用价值和现实意义。苏绣的数学化，一方面是对苏绣艺术本体语言的进一步探索，另一方面也为苏绣机器人的研发奠定了算法基础。

迄今为止，刺绣机还难以企及苏绣手工刺绣的精度。以算法为基础、具有学习功能的苏绣机器人，将通过向苏绣大师学习达到接近的刺绣效果。不过，这并非是要取代苏绣大师，而只是将心手合一的艺术创造过程中可重复的部分提取出来，进行摹仿和复制。

苏绣的入门时间很长，完成单件作品的时间也很漫长，如今苏州地区愿意以刺绣为业的年轻人越来越少。一位苏绣大师终其一生所能完成的杰作是十分有限的，通过刺绣机器人的创造性临摹，其作品可以被无限复制和衍生，在走进千家万户、美化人民生活的同时，也能为从业者赢得另一份回报。这或许是缓解苏州地区苏绣后继无人之困境的方法之一。

在姚惠芬、俞宏清的热情支持下，在清华大学丘成桐数学科学中心两位老师的热心帮助下，2021年初，我们在传统工艺与材料研究文化和旅游部重点实验室下组建了一个“苏绣数学化与智能生产”课题组，并得到了清华大学文科建设“双高”计划的资助。

课题组目前已成功地将所有可能的苏绣针法进行了函数轨迹运算，初步编成了计算机程序。基于原有的苏绣针法、算法和程序所生成的几种新的苏绣针法，已被姚惠芬用于刺绣创作。本文所描述的是苏绣数学化所取得的第一阶段成果。目前，本课题还在进行之中。

二、苏绣与数学——两种语言的沟通

针法不仅是苏绣的本体特征，同时也是苏绣的创作语言。现有记录在冊的苏绣针法数量约40余种，个别针法具有多种名称，但本质不变。统览苏绣绣谱及资料，如《雪宦绣谱》《苏绣技法》等，针法的记录和解说以文字说明为主，图片示例为辅，需要阅读者有相当的基础;影像类记录以拍摄刺绣手法为主，难以兼顾绣布上下两方空间，以个人为拍摄对象的记录内容缺乏一致性。将刺绣抽象成为线在空间中的运动轨迹，通过数学语言将其重新归纳，将有助于解决上述问题。可以预见的是，将针法转换为数学语言后，其“沟通”范围逐步扩大。数学无疑是人类的底层逻辑之一，是各类学科、技术与创作的基础语言，将苏绣针法以数学语言进行转译，是“具体—抽象—具体”的转换过程，为苏绣与其他媒介类型艺术之间的沟通搭建了桥梁。

拓扑学着重于研究物体的位置关系，并可以将位置关系通过拓扑学语言实现标准化表述。而作为苏绣最核心特征的针法，其本质也可以视为是针线在特定空间上的连续移动轨迹，或者说其空间位置连续变化的轨迹。因此，苏绣的针法纷繁复杂，但专门研究连续性的拓扑学，仍可以通过对针线空间移动轨迹对针法实现拓扑学意义上的模拟。甚至可以说，拓扑学与苏绣针法具有天然的契合性。

本着以上思路，我们对苏绣现有针法进行了梳理。作为课题合作方，姚惠芬、俞宏清老师对苏绣针法进行了专业细致地讲解，姚惠芬带领工作室团队对每一种针法进行示范，并为针法的分类及针线的运动轨迹提出了宝贵建议。综合上述研究，我们对苏绣针法进行了如下分类整理：

1.针法分类

苏绣针法的分类方法多种多样，传统分类以平绣、条纹绣、点绣、编绣、网绣、纱绣、缤纹针、变体绣和辅助针法9大类;有学者结合西方绘画方法，将针法看作是“点、线、面”的造型单位。[2]我们将苏绣针法放在坐标系中观察可见，各类针法的核心区别在于，线段的起点、落点及在空中扭曲的形态。因此，针法可以分成以下8类：

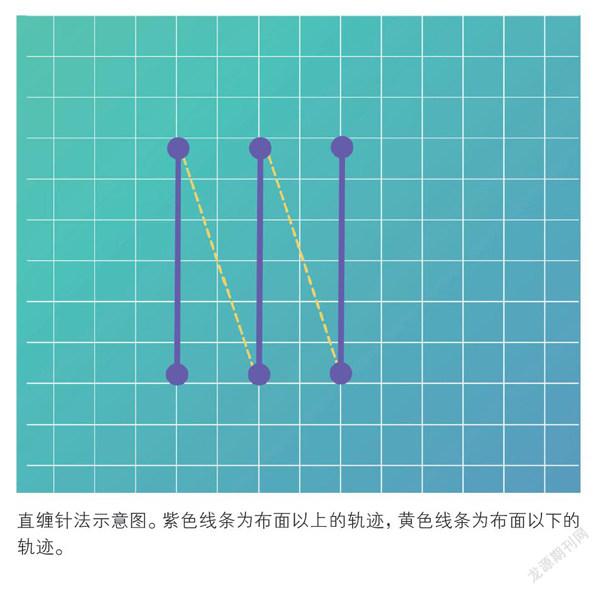
a.平绣类：以线段间首尾相连为排线方法，出针及入针所形成轨迹可视为线段函数相连;该类型包括齐针（直缠、横缠、斜缠）、抢针（正抢、反抢、迭抢）。

b.套针类：排线特点以线段间互相穿插为特点，要求第二层线段要在第一层线段间穿插，并以此类推，达到区域面积铺面效果。该类型包括套针（平套、散套、集套、擞和针、施针）。

c.条纹类：该类针法以较短线段为造型基础单位，线段间互相连接或部分重合，以组成不同曲度及长度的线条或面积。该类型包括接针、切针、滚针。

d.线圈类：该类针法以“圈”环环相绕，形成或敞口或闭合的链状线条。该类针法分为两种完成方法，分别为：以一线绕圈前后连接，或以两线进行，一线绕圈一线固定。该类型包括辫子股、拉锁子、链条绣等。

e.绕线类：该类针法以“盘、绕”为特点，一条线扭曲造型后以另外一线进行固定。该类型包括平金绣、盘金绣。

f.打结类：该类针法以“结”为特征，即线段在空间中旋绕成结，并固定在平面之上，以“结”作为造型基本单位。根据成结的形状，可以分为打籽绣、结子绣、拉尾子。

g.三角类：该类针法以“三角形”作为基本造型单位，通过组合形成“菱形”“六边形”等形状进行造型。

未包含在上述针法的其他针法主要包括编织类，如编针、格锦、咇绒等，以经纬线编织而成，刺绣的运动轨迹是在不同空间中穿梭，而此类绣法属于在平面上移动;而定点类针法，如戳纱、打点、纳锦、松针、挑花、桂花针等，均将底布视为格，以数格定点的方式排列图案，本身针法并无特异;辅助类针法，如铺针、扎针、刻鳞针等，均为表现特定质感的针法，其刺绣方法以齐针及套针为基础，根据图案进行调整，针法没有形成特殊轨迹。

2.要素提取

针法在空间中的运动轨迹提示了一种新的可能，即利用拓扑学中的标记语言将针法总结为5种要素间的关联体系，每种针法由标准公式和运动数据共同定义。具体公式说明如下：

Module X = （A，B，K，L，P）

A：表示出针位置坐标，如【（0，0），（0，1），…】;

B：  表示入针位置坐标，如【（1，0），（2，0），…】;

K：  表示是否有扭结及个数， {K=0或null，表示无打结};{K=1，2…，表示相应打结次数};

L：  表示该针轨迹与下一针轨迹间的关系，{L=0或null，表示正常连接};{L=1， 表示特殊连接};

P：判断针法是否为双线运行，即是否为盘金绣，{P=0或null，表示非盘金绣};{P=1，表示是盘金绣};

3.重新定义

根据上述公式及公式解析，每一种针法均可以该公式进行定义。以苏绣针法中较为常见的切针为例，具体说明如下：

Module QZ = （A，B，K，L，P）

其中，K=L=P=0，即无扭结，两针间无特殊相连，非盘金绣;

其中，赋值A=（1，2）…，赋值B=（3，2）…

因此，某一切针的轨迹可以定义为：

{[（1，2），（3，2），0，0，0]，[（3，2），（5，2），0，0，0]，[（5，2），（7，2），0，0，0]}

以此类推，可获知其他针法的定义及轨迹。

4.函数表达与轨迹模拟

上述对针法的分类及标记语言重新定义了针法的含义，每一种针法可以理解为5种要素的判断及相互关联，此种语言以最为底层的数学表达进行记录，既可以让人学习了解，同时也为转换为机器语言打下了基础，成为人与机器同步理解针法的核心。对于人与机器均可理解该语言，通过将具体针法函数化的方法即可证明。

针法的函数建模公式主要由K、P、L的取值范围决定，具体可分为6种不同的函数方程。通过对以上基本变量的不同赋值，不同的函数方程可以形成不同的针法运行轨迹。

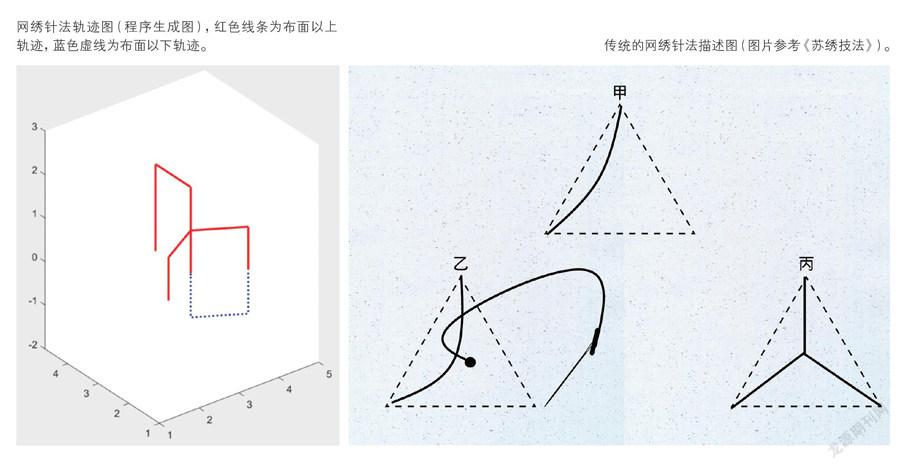
通过对针法函数方程的梳理，基本明确了针法随时间变化而生成的轨迹。选取Matlab作为建模软件，并将针法与函数建立对应模型。软件通过读取（A，B，K，P，L）的数值控制参数方程的变化，以网绣针法为例，输入相应数据后，其轨迹图显示如下：

5.针法创新

针法的建模函数会因输入数据的不同而产生变化，随着空间坐标的不断扩展以及K值的变动，在三维空间中不断扭曲旋转的函数随之生成，新函数群的诞生意味着新针法的可能性。不断生成的函数与现有针法体系的对比实验，将在一定程度上识别出可能存在的新针法。从函数到针法间的转换关键点在于：对函数特征的识别以及线拉直受力后的形态分析。根据上述原理，对所进行的针法创新实验如下：

1）运行针法函数程序数次，输入不同参数后产生变化不一的函数若干;

2）将第一步运行产生结果函数与已知的针法函数模型进行一一比对，选出不在已知针法体系中却符合针线运动基本规律的运行结果，明晰其运动过程;

3）将所选函数的分段表达视为针线在空中运动的轨迹，绘制三维空间内的运行轨迹，以及模拟针线受力后的平面图。

4）使用平面模拟图与绣娘沟通，达到以下目的：確认其创新性与已知针法无重复;确认实际可应用性。

5）由绣娘使用上述新针法，选择合适表现对象进行设计并完成作品刺绣。

新针法的应用作品由姚惠芬设计完成，她在仔细研究新针法后，设计了数种刺绣方案，表现对象从具象物体到抽象图案均涵盖其中。经不断调整及反复比对后，最终选择“蒲公英”的植物图案为主体，既呈现出蒲公英的特有质感，又体现出新针法的抽象简洁之美，是针法特质与表现对象的高度契合。

针法的创新与成功应用具有深远意义，苏绣在漫长的历史中不断衍生出新的针法与设计理念，其根源来自针法的不断实践，需求促进针法的前进，以打籽绣为例，其针法易学，既能表现多种形态又能增加织物的耐磨性，是美观与实用性的结合;另一个层面来看，以乱针绣为代表的模仿“素描”“油画”等西方艺术形式的针法，是时代变革与苏绣走向艺术领域的双重作用之下的结果。时至现代生活，苏绣作为曾经的实用品属性逐渐退出历史舞台，随着市场需求的下降以及从业人员的不断减少，苏绣的针法创新也走向了瓶颈;作为具有欣赏功能的苏绣作品来说，对表现形式的突破也是其内在要求。现代科技的发展，尤其是计算机作为辅助设计工具，为解决上述问题提供了可能，正如上述新针法的生成与应用，为苏绣既有针法的标准化保存找到了答案，也提供了“数学—针法—设计”这样一条创新路径，而创新针法的诞生无疑将为苏绣的发展带来新的契机。

三、总结与探索

苏绣，并不只是一门传统工艺，它拥有广泛的外延。数学，并不局限在理论世界，它拥有强大的抽象与创新能力。苏绣与数学的结合，以苏绣的本体——针法作为最佳的切入点，传统的针法在现代科学中得以重新解读与释放，也为苏绣的创新与应用开辟了新的方向。首先，苏绣与数学的结合，可以促进苏绣的保护与继承。过去苏绣继承面临的困难就在于难以通过文字和图像进行知识传播，主要依赖口口相传和亲身示范。通过与数学结合的形式，形成标准化针法语言，既能精准记录刺绣技艺，又提供了高效传播的可能性。第二，苏绣与数学的结合，为苏绣产业的发展提供了新的空间。通过苏绣与数学的结合，可以拓展苏绣产业的覆盖领域范围，例如可以延伸至数字空间中的苏绣教学。通过在新的形式上拓展苏绣产业的覆盖领域，使苏绣产品的概念更加丰富，有助于苏绣产业今后更好地发展。

目前，对苏绣与拓扑学，乃至其他科学门类的结合仍然处于探索和积累阶段。对传统的继承与深度挖掘，全新理念的涌现，都将为古老而年轻的苏绣走入人们的现代生活、重新焕发生命力带来新的可能与方向。

*本文为传统工艺与材料研究文化和旅游部重点实验室2021年专项课题《苏绣数学化与智能生产》阶段性成果，得到了清华大学丘成桐数学科学中心的技术支持。

参考文献

[1] 陈岸瑛.从苏绣能否成为当代艺术谈起[J].艺术设计研究，2018（01）：5-8.

[2] 蔡子芬， 叶洪光. 浅析传统刺绣针法中"点线面"的表达[J]. 纺织科技进展， 2021（02）：10-12，32.